Граничные условия для векторов электрического поля.

Рис.16(а).

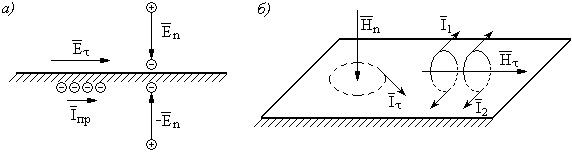
Рис. 16. К определению граничных условий для векторов электрического (а) и магнитного (б) полей: - нормальная составляющая вектора напряженности электрического поля; - тангенциальная составляющая вектора напряженности электрического поля; - нормальная составляющая вектора напряженности магнитного поля; - тангенциальная составляющая вектора напряженности магнитного поля

Составляющая вектора электрического поля возле проводящей поверхности вызывают перераспределение зарядов. Поскольку тангенциальная составляющая направлена вдоль поверхности проводника, то это эквивалентно протекающему поверхностному току проводимости . Поскольку направленны синфазно то они имеют активный характер сопротивления, следовательно, имеют тепловые потери энергия и тангенциальная составляющая затухает. Нормальная составляющая порождает свое зеркальное отражение и поскольку направленны противофазно то это говорит о наличие реактивности и об отсутствии тепловых потерь. Таким образом около проводящей поверхности граничными условиями для векторов электрического поля будут являться .

Граничные условия для векторов магнитного поля.

Рис.16(б). Нормальная составляющая вызывает в проводнике поверхностные вихревые токи за счет которых затухает. Тангенциальная составляющая вызывает токи в воздухе и в тонком слое проводника. Токи направлены противофазно и следовательно затухание отсутствует. Таким образом около проводящей поверхности за счет вихревых токов затухает, а порождает незначительные токи проводимости и поэтому распространяется практически без затуханий. Таким образом около проводящей поверхности граничными условиями для векторов магнитного поля являются из всего сказанного запишем граничные условия векторов электромагнитного поля около проводящей поверхности Данные граничные условия справедливы для статических (неподвижных), стационарных (с одной скоростью) и переменных эл-маг полей. Рассмотрим решение мембранных уравнений с точки зрения теории мембран Рис.17.

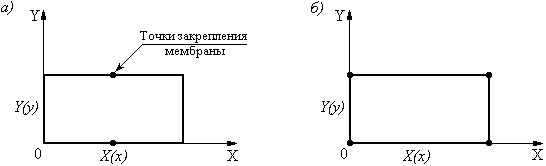
Рис. 17. К решению мембранных уравнений с точки зрения теории мембран

В первом случае Рис.17(а) максимальные колебания будут наблюдаться вдоль плоскости Z0Y. Поскольку плоскость Z0Y является проводником то исходя из граничных условий это соответствует , следовательно Рис.17(а) является характеристикой волн типа Н в прямоугольном волноводе. Во втором случае Рис.17(б) максимум колебаний соответствует это соответствует направлению следовательно Рис.17(б) является характеристикой волн типа Е в прямоугольном волноводе. Поскольку функции Х(х) и Y(y) независимы друг от друга то следовательно и распределение полей по осям и х и у независимо. Каждое из таких распределений характеризуется индексами n и m Рис.18

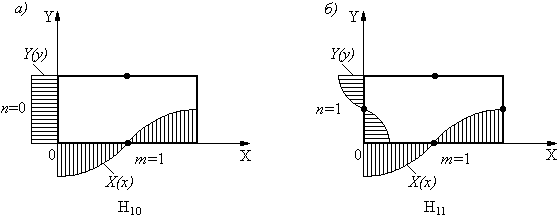
Рис. 18. К определению понятий индексов m и n

Индекс m показывает кол-во стоячих полуволн укладывающихся на расстоянии а вдоль оси х. Индекс n показывает кол-во стоячих полуволн укладывающих на расстоянии b вдоль оси y. Минимальные значения этих индексов соответствуют волне , которая и является основной волной прямоугольного волновода.