Двойное дроссельное соединения коаксиальной линии.

Рис.45. Двойные дроссельные соединения отличаются тем что как внешний так и внутренний проводник соеденины с помощью искуственных коаксиальных линий. Вкладыш 1 Рис.45 состоит из двух частей подвижных друг относительно друга и пружины Рис.46. Дроссельное соединение Рис.45 состоит из двух короткозамкнутых коаксиальных полуволновых линий АВС и DEG включенных последовательно в основную линию передач. В этих линиях образуется стоячая волна тока с узлами тока в точках B и E и пучностью тока в точках A и D Рис.37 Механическое соединение двух отрезков линий происходи в точках B и E где находится узел тока( ) и следовательно качество контакта в этих точках не играет существенной роли. По той же причине излучение энергии через возможные зазоры связанные с неплотным прилеганием поверхностей будет небольшим. В точках A и D входное сопротивление боковых линий будет равно ( ) и поэтому одна секция подсоединяется к другой без какого либо переходного сопротивления. Рассмотренный принцип работы соединения справедлив только для одной фиксированной длинны волны. Для улучшения согласования участки АВ и DE делают с меньшим волновым сопротивлением чем волновые сопротивления основной линии и участков BC и EG. Для расширения полосы пропускания соединения рекомендуется сдвигать зазоры во внутренних и внешних проводниках (точки А и D )относительно друг друга на расстояние (т.е. вкладыш 1 на Рис.45 смещается в точку D).

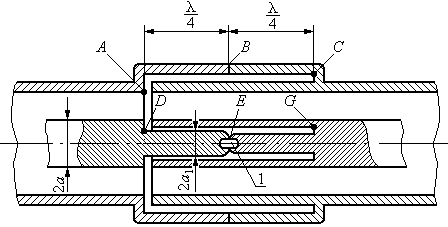
Рис. 45. Двойное дроссельное соединение коаксиальных линий: 1 – вкладыш

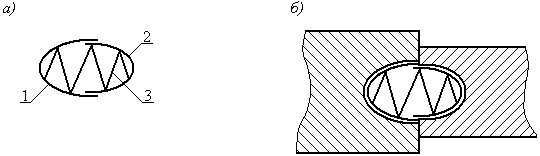
Рис. 46. Конструкция вкладыша (а) и соединение с помощью вкладыша (б): 1, 2 – составные части вкладыша; 3 – пружина

Для рассмотренного дроссельного соединения передаваемая по линии мощность снижается до величины (65)Где a₁ и a обозначены на Рис.45; Р-мощность в линии при отсутствии соединения. Данное соединение может работать в полосе частот до 20% ( ). Принцип работы двойного дроссельного соединения применяется во вращающемся коаксиальном дроссельном соединении.

Изгибы линии передач. Изгибы волноводных линий.

При создании тракта СВЧ любой радиотехнической системы возникает необходимость изгибать линии передачи под различными углами. При этом резкие изгибы создают отражение за счет возбуждения полей нераспространяющихся волн высших типов в которых происходит накопление электромагнитной энергии. Для минимизации отражений изгибы дополняют различными согласующими элементами. Волновод можно изгибать как по широкой стенке (изгиб в плоскости электрического поля Е-изгиб) так и по узкой (изгиб в плоскости магнитного поля или Н-изгиб). Эффективным способом уменьшения отражений в изгибах прямоугольного и круглого волноводов, является подрезание углов. Прямоугольные изгибы- это так называемые одинарные уголковые изгибы приведены на Рис.47 (а и б). На Рис.47 (в) приведена примерная картина распределения силовых линий электрического поля вместе изгиба прямоугольного одинарного Е-уголка.

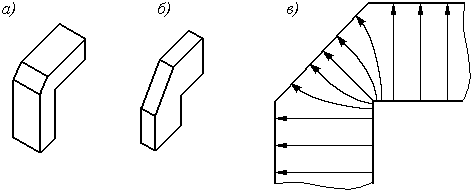
Рис. 47. Прямоугольные изгибы: а – Е-уголок; б – Н-уголок; в – распределения силовых линий электрического поля в Е-уголке

Оптимальные размеры Е и Н одинарных уголков могут быть определены из графиков приведенных на Рис.48 (а и б) соответственно. Концентрация силовых линий электрического поля в области резких изгибов Рис.47 (в) снижает электрическую прочность тракта. Данный недостаток в значительной степени устраняется в двойных поворотах и в плавных изгибах.

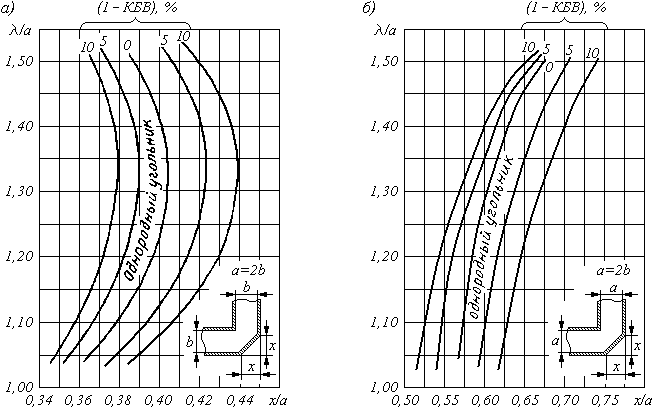
Рис. 48. Графики для определения оптимальных размеров Е-уголка (а) и Н-уголка (б)

Более широкополосными являются уголки с двойным поворотом под 45⁰ Рис.49. Улучшение согласования происходит как за счет уменьшения отражений от каждой нерегулярности (поворот) так и за счет взаимной компенсации отражений от них. Повороты располагаются на расстоянии L Рис.49.

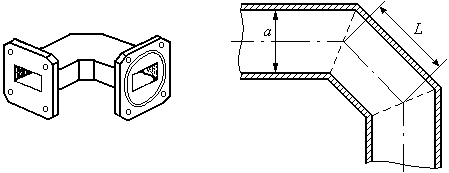
Рис. 49. Прямоугольный изгиб с двойным поворотом (Н-уголок)

Значение L для E-уголка берется четверть волны в волноводе для H-уголка L определяется по графику Рис.50.Плавные изгибы так же бывают в плоскостях E Рис.51 (а) и H Рис.51(б). В таких изгибах отражения создаются у каждого конца изгиба. Причем такие отражения сильно зависят от тщательного изготовления изгиба и деформации стенок при изгибе. Для компенсации отражений изгиб должен иметь среднюю длину L примерно равную целому числу полуволн. При внутреннем радиусе изгиба и хорошем качестве изготовления изгиба можно достичь достаточно хорошего значения КБВ.

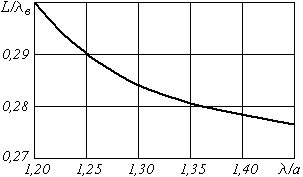
Рис. 50. График для определения оптимальных размеров двойного Н-уголка

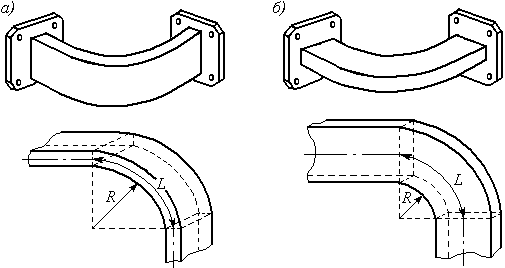
Рис. 51. Плавный изгиб прямоугольного волновода в плоскости Е (а) и в плоскости Н (б)