Федеральное агентство морского и речного транспорта

Федеральное бюджетное образовательное учреждение

высшего профессионального образования

«Волжская государственная академия водного транспорта»

Кафедра прикладной механики

и подъёмно-транспортных машин

Основы

теории надежности и диагностики

подъемно-транспортных машин

Определение критериев надежности

Методические указания

для студентов очного и заочного обучения специальности

190602 «Эксплуатация перегрузочного оборудования портов

и транспортных терминалов»

Составители – Н.С. Отделкин, Д.Н. Костюничев

Нижний Новгород

Издательство ФБОУ ВПО «ВГАВТ»

2011

УДК 621.86-192

О75

Основы теории надежности и диагностики подъемно-транс-портных машин. Определение критериев надежности : метод. указания для студ. оч. и заоч. обуч. специальности 190602 «Эксплуатация перегрузочного оборудования портов и транспортных терминалов» / сост. – Н.С. Отделкин, Д.Н. Костюничев. – Н. Новгород : Изд-во ФБОУ ВПО «ВГАВТ», 2011. – 36 с.

Изложены основы теории надежности и методика расчёта критериев надежности восстанавливаемых и невосстанавливаемых изделий. Даны типовые задачи и варианты заданий.

Для студентов очного и заочного обучения, выполняющих расчётные работы по дисциплине «Надежность и безопасная эксплуатация подъемных сооружений».

Отв. редактор – доцент, канд. техн. наук В.П. Захарцев.

Работа рекомендована к изданию кафедрой прикладной механики и подъемно-транспортных машин (протокол № 6 от 04.02.2011 г.).

© ФБОУ ВПО «ВГАВТ», 2011

Введение

Методические указания предназначены для студентов старших курсов специальности 190602 «Эксплуатация перегрузочного оборудования портов и транспортных терминалов» для более глубокого изучения дисциплины «Основы теории надежности и диагностики подъемно-транспортных машин».

Цель методических указаний – помочь студентам специальности 190602 изучить основы теории надежности и приобрести навыки ее применения к решению прикладных инженерных задач.

В каждом разделе приводятся теоретические положения с расчетными формулами, типовые задачи с примерами и варианты заданий с исходными данными. Варианты заданий назначаются преподавателем.

1. Определение критериев надежности

невосстанавливаемых объектов

1.1. Теоретические положения

о надежности невосстанавливаемых объектов

К числу невосстанавливаемых объектов относятся такие объекты, которые в случае возникновения отказа не могут быть восстановлены или отремонтированы, то есть невосстанавливаемые объекты работают до первого отказа. Например, грузовой канат или подшипник качения являются невосстанавливаемыми объектами.

Основными критериями надежности невосстанавливаемых объектов являются:

– вероятность безотказной работы;

– частота отказов ;

– интенсивность отказов ;

– средняя наработка до первого отказа.

Перечисленные критерии надежности связаны между собой, и, используя эти уравнения связи, можно вычислить по одним критериям другие. Вероятностью безотказной работы называется вероятность того, что при определенных условиях эксплуатации в заданном интервале времени или в пределах заданной наработки не произойдет ни одного отказа.

Согласно определению

,

(1.1)

где	–	время, в течение которого определяется вероятность безотказной работы;
	–	время работы элемента от начала до первого отказа.

Вероятность безотказной работы по статистическим данным об отказах оценивается выражением

,

(1.2)

где – число элементов в начале испытаний;

– число отказавших элементов за время .

При большом числе изделий статистическая оценка практически совпадает с вероятностью безотказной работы .

На практике иногда более удобной характеристикой является вероятность отказа.

Вероятностью отказа называется вероятность того, что при определенных условиях эксплуатации в заданном интервале времени возникнет хотя бы один отказ, то есть

, .

(1.3)

Отказ и безотказная работа являются противоположными и несовместимыми событиями, поэтому

.

(1.4)

Частотой отказов называется отношение числа отказавших элементов в единицу времени к первоначальному числу испытываемых элементов при условии, что все вышедшие из строя элементы не восстанавливаются:

,

(1.5)

где – число отказавших образцов в интервале времени от до .

Частота отказов есть плотность вероятности (или закон распределения) времени работы изделия до первого отказа. Поэтому

.

(1.6)

Интенсивностью отказов называется отношение числа отказавших изделий в единицу времени к среднему числу изделий, исправно работающих в данный отрезок времени:

,

(1.7)

где – среднее число исправно работающих изделий в интервале времени .

,

(1.8)

где – число изделий, исправно работающих в начале интервала времени ;

– число изделий, исправно работающих в конце интервала времени .

Выражение (1.7) есть статистическое определение интенсивности отказов. Вероятностная оценка этой характеристики находится из выражения

.

(1.9)

Интенсивность отказов и вероятность безотказной работы связаны между собой зависимостью

.

(1.10)

Средней наработкой до первого отказа называется математическое ожидание времени работы изделия до отказа.

Как математическое ожидание вычисляется через частоту отказов (плотность распределения времени безотказной работы):

.

(1.11)

Так как положительно и , а , то

.

(1.12)

По статистическим данным об отказах средняя наработка до первого отказа вычисляется по формуле

,

(1.13)

где – время безотказной работы і-го изделия.

Из формулы (1.13) следует, что для определения необходимо знать время выхода из строя всех испытуемых изделий, поэтому пользоваться этой формулой неудобно. Имея данные о количестве вышедших из строя изделий в каждом і-м интервале времени, величину лучше определять из уравнения

.

(1.14)

Величины и , входящие в уравнение (1.14), находятся по следующим формулам:

; ,

где – время начала і-го интервала;

– время конца і-го интервала;

– время, в течение которого вышли из строя все элементы.

Одной из наиболее полных характеристик надежности невосстанавливаемых объектов является интенсивность отказов . Эта величина определяет надежность объекта в каждый данный момент времени.

Используя статистические данные о работе объекта, можно построить гистограмму интенсивности отказов для промежутков времени (рис. 1).

Кривая интенсивности отказов может быть получена соединением центров вершин прямоугольников гистограммы. Обычно эта кривая имеет вид, приведенный на рис. 1. На кривой видны три характерных участка: I участок – интенсивность отказов монотонно убывает (период приработки); II участок – интенсивность отказов постоянна (период нормальной эксплуатации); III участок – интенсивность отказов возрастает (период старения или износа).

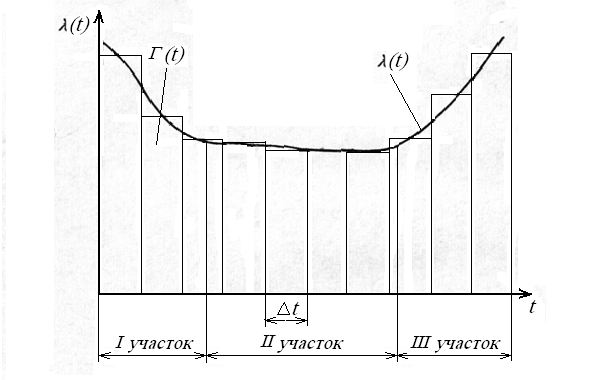
Рис. 1. Гистограмма

и кривая интенсивности отказов

При изучении надежности технических устройств наиболее часто применяются следующие законы распределения времени безотказной работы: экспоненциальный, нормальный, Релея, Гамма и Вейбулла.

В практике широкое распространение получила экспоненциальная модель, при которой критерии надежности связаны между собой следующими зависимостями:

; ; ; .

(1.15)

Показатели надежности невосстанавливаемых объектов на периоде старения описываются нормальным или логарифмически нормальным законами распределения. Для этих законов постепенных отказов характерно то, что в начале имеется низкая плотность распределения, после максимум, а затем падение, обусловленное уменьшением числа работающих элементов.

Вероятность отказа и вероятность безотказной работы в этом случае определяются через квантили, соответственно и , по выражениям:

, ,

(1.16)

где – среднее время безотказной работы (параметр нормального распределения);

– среднеквадратическое отклонение (параметр нормального распределения).

Остальные критерии надежности при нормальном законе распределения рассчитываются по формулам:

; ; ; .

(1.17)

Приведенные выше критерии служат критериями надежности отдельных элементов объектов или систем.

При оценке надежности систем необходимо учитывать различные виды соединения элементов, входящих в эти системы. Различают системы с последовательным, параллельным и комбинированным взаимодействием элементов. На рис. 2 приведена блок-схема различных видов взаимодействия между элементами, образующими систему.

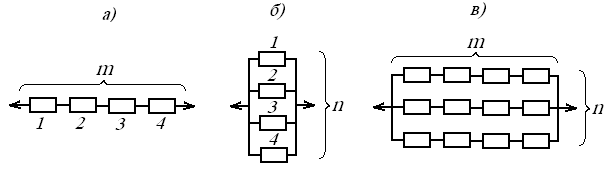
Рис. 2. Блок-схема различных видов взаимодействия

между элементами, образующими систему:

а) последовательное; б) параллельное; в) комбинированное

В системах с последовательным соединением элементов (рис. 2, а) отказ любого элемента приводит к отказу всей системы. Надежность таких систем всегда ниже надежности самого ненадежного элемента. К таким системам относится большинство подъемно-транспортных машин и приборов.

Вероятность безотказной работы системы с последовательным соединением элементов (отказы элементов происходят независимо) рассчитывается по формуле

,

(1.18)

где – вероятность безотказной работы элементов.

Интенсивность отказов системы с последовательным соединением элементов при условии, что интенсивности отказов каждого элемента системы равны между собой, составит

.

(1.19)

Один из способов повышения надежности системы заключается в резервировании или в параллельном соединении элементов (рис. 2, б).

В системах с параллельным соединением элементов отказ наступает только при отказе всех элементов. Для таких систем вероятность безотказной работы определяется по выражению

,

(1.20)

где – вероятность отказа одного элемента;

– вероятность отказа всех элементов или системы.

Интенсивность отказов такой системы определяется как сумма интенсивностей отказов всех элементов системы, то есть

.

(1.21)

Выражение для определения вероятности безотказной работы для систем с комбинированным взаимодействием элементов (рис. 2, в) имеет вид

.

(1.22)

При подготовке к занятиям по данной теме рекомендуется использовать источники [2, 5].