Неперервні випадкові величини. Означення 1. Вв називається неперервною, якщо її функція розподілу неперервна в будь-якій точці та диференційовна всюди крім, можливо, окремих точок.

Типовий графік функції розподілу неперервної ВВ наведений на рис 6.2. Функція розподілу на рис 6.2 не диференційовна в точках . Неперервну ВВ можна визначити за допомогою іншої функції , яка називається щільністю рлзподілу ймовірності неперервної ВВ Х. Означення 2. ВВ називається неперервною, якщо існує така невід’ємна функція , яка називається

Рис. 6.2

щільністю рлзподілу ймовірності ВВ Х, що для кожного

. (2)

Властивості щільності ймовірності:

1. -ця формула виплиаає з властивості (4) функції розподілу;

2. .

3) (умова нормування, яка означає, що площа під кривою з рівнянням і віссю 0х дорівнює одиниці ;

4) в точках неперервності .

8. Числові характеристики випадкових величин

Математичним сподіванням (м.с.) випадкової величини (ВВ) називається число , яке в залежності від типу ВВ визначається за формулою

Математичним сподіванням функції ВВ називається число

Дисперсією ВВ називається невід'ємне число .

При підрахуванні дисперсії часто використовують формулу .

Дисперсія характеризує розсіювання ВВ навколо математичного сподівання

Розмірність дисперсії дорівнює квадрату розмірності ВВ . Тому зручно з практичної точки зору приймати як міру розсіювання ВВ середнє квадратичне (стандартне) відхилення , вимірність якого співпадає з вимірністю ВВ .

Чим менше ( ), тим тісніше групуються значення випадкової величини навколо її математичного сподівання.

Приклад 2. Щільність ймовірності ВВ

Знайти: 1) А; 2) та побудувати її графік; 3) ; 4) ; 5) ; 6) .

Розв’язання. 1) Сталу А знаходимо з умови нормування;

А .

2 .

3) = .

4) . == –

5) .6) = =1 = =1 = = .

5. Завдання із статистики.

1. Початкові дані – 36 значень випадкової величини

Розбиваємо виборку на 6 проміжків рівної довжини:

7.52, 7.88, 8.88, 8.98, 9.36, 9.48, 9.56, 9.72, 10.34, 10.36, 10.36, 10.38, 10.38, 10.44, 10.80, 10.80, 11.20, 11.22, 12.20, 12.32, 12.40, 12.70, 12.70, 12.88, 13.08, 13.80, 13.82, 14.46, 14.68, 14.76, 15.40,15.66,15.78, 15.88, 16.86, 17.10,

де ,

2. Групуємо вибірку по 6-ти проміжках;

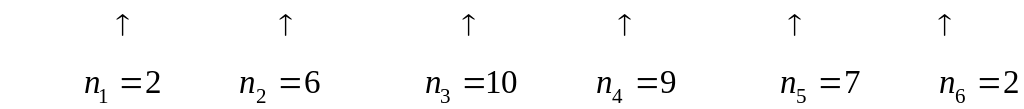
3.Будуємо гістограму, де числа – довжини стовпчиків

100	4.Знаходимо вибіркове середнє та дисперсію: =12.05; 6.6046; 2.5699;

5. Довірчі інтервали рівня значущості для математичного сподівання та середнього квадратичного відхилення . .

;

0.845 1.23

0.819 1.28

,0.772 1.40

8