1.4.4. Асимптотичні формули для схеми Бернуллі

Формула (1) приводить до громіздких обчислень при великих значеннях n і k, а також при малих значеннях p або 1– p. Тому, доцільно мати наближені, але прості формули для розрахунку відповідних ймовірностей ,або їх сум..

1) Формули Муавра-Лапласа. Локальна формула :

.

(2)

має місце при p і 1-p істотно відмінних від 0 і великих значеннях n і k . Відносна похибка цієї формули зменшується при зростанні n і зменшенні |k-np|. Вона застосовується звичайно при n >100, np(1– p)20 і |k- np |< <3 .

Приклад. Знайти ймовірність того, що подія А настане k=85 раз при n=400 випробуваннях, якщо ймовірність появи події А в кожному випробуванні дорівнює p=0.2.

Розв’язання. n=400, p=0.2. np=400 0.2=80, np(1– p)=80 0.8=64, =8,

k-np=85-80=5, 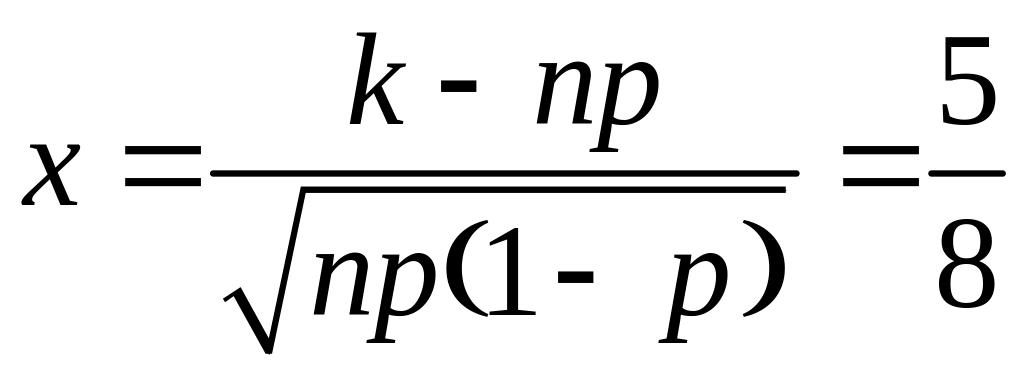=0.125 5=0.625

Інтегральна формула :

.

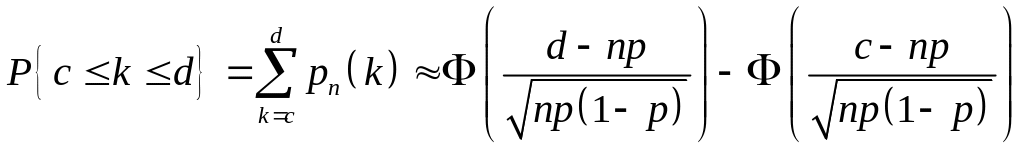(3)

де 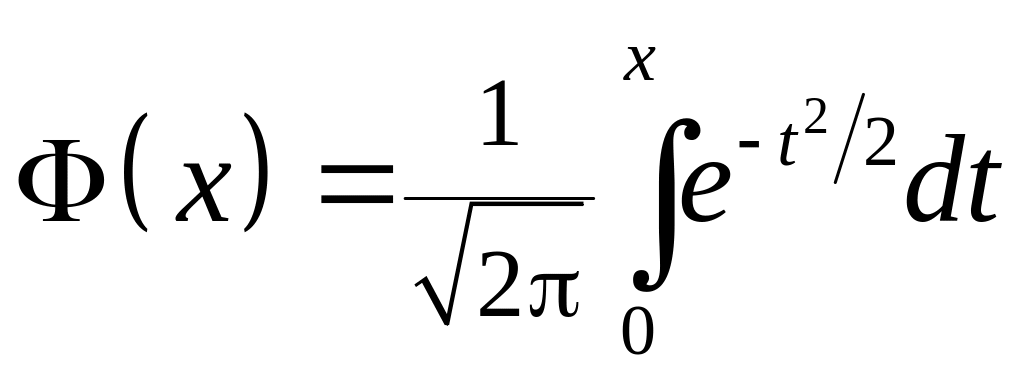так звана функція Лапласа (або інтеграл помилок). Значення цієї непарної функції наведені в таблиці 1 додатка, а її графік­ на рис. 1.17. Формула (4) є твердженням теореми Муавра-Лапласа з пункту 3.2.4. Вона використовується тоді, коли і формула (3 )

.

Приклад 2. Гральний кубик підкидається 1200 раз. Знайти ймовірність того, що кількість випадань одиниці знаходиться в діапазоні між 195 та 210 включно. Розв’язання.Оскільки n=1200, p=1/6, то маємо = = . Подальше обчислення пов’язане з великими труднощами. Тому скористаємося формулою (3). Оскільки np200, , d– np 10, c– np  – 5, шукана ймовірність приблизно дорівнюватиме

Рис.1.7

Розділ 2. Випадкові величини

Означення 1. Випадковою величиною називається змінна величина, набуваємі значення якої залежать від наслідку експерименту (заздалегідь, до проведення експерименту, визначити, яке значення прийме величина неможливо ). Інакше кажучи, випадковою величиною називається числова функція, яка визначена на просторі елементарних подій .

Для позначення випадкової величини найчастіше використовуються великі літери X, Y, Z латинського алфавіту, а для їх можливих значень – відповідні малі літери x, y, z.

Наведемо кілька прикладів випадкових величин: 1) кількість влучень у ціль при п‘яти пострілах; 2) кількість відмов приладу протягом заданого проміжку часу; 3) тривалість проміжку часу очікування трамвая або автобуса на зупинці; 4) результат вимірювання фізичної величини; 5) відстань від точки влучення в мішень до її центра .

Випадкова величина дає змогу разом з простором  розглянути інший більш простий простір ₁ у якому елементарні події є значеннями випадкової величини.

Означення 2. Функцією розподілу випадкової величини X називається задана на всій осі Ox функція , яка визначається співвідношенням

	.	(1)
Рис. 2.1

Відзначимо таки властивості функції розподілу:

1) ( ймовірність довільної події належить відрізку [0;1] );

2) = , а подія {X< } є неможливою ) ;

3) а подія { X<+ }є вірогідною );

4) F_X (x) є неспадною функцією змінної х (якщо с<d , то подія {X<d} є сумою несумісних подій {X<c} і { X<d} (рис. 2.1)

5) функція F_X (х ) в довільній точці є неперервною зліва.

Знаючи функцію розподілу, можна знайти ймовірність того, що випадкова величина попадає у проміжок [c; d) (рис.2.1.)

P{X[c; d)} = P{X < d}–P{X < c} =FX (d) – FX (c)..

(2)

.

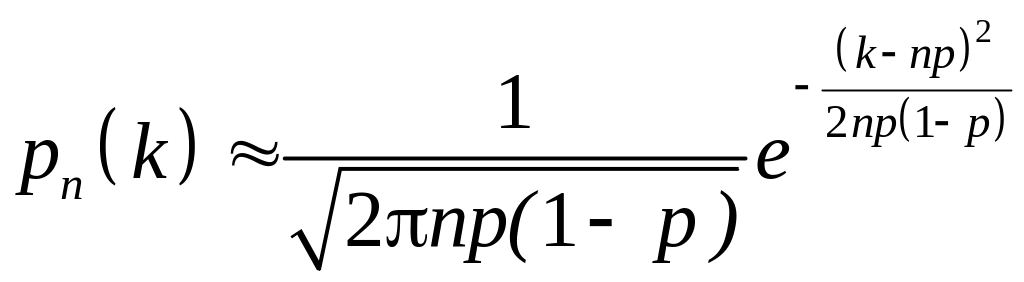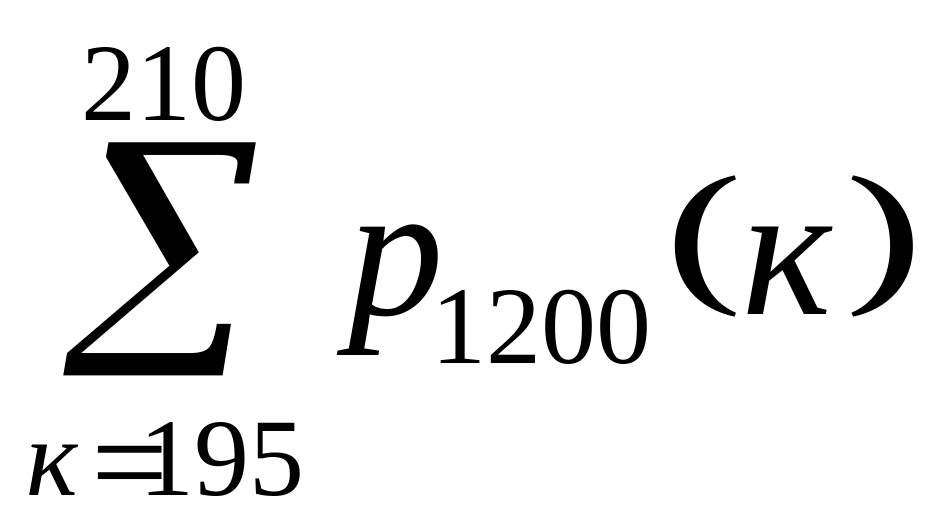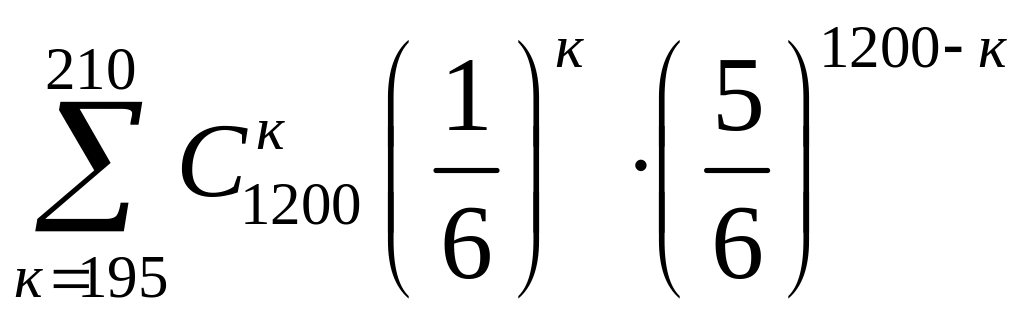10