7. Закон Кулона и уравнение электростатики в вакууме

Электростатика – закон электромагнетизма, в котором изучаются неподвижные заряды и связанное с этими зарядами электрические поля. (или: электрическое поле неподвижных зарядов наз. электростатическим).

Неподвижных зарядов не существует, т.е. существует электрический ток и магнитные поля. Раздел электростатика является простой моделью для исследования электрического поля отдельно от магнитного. Эту модель можно объяснить направленным движением зарядов. В большинстве случаев законы электростатики не применимы, но применимы для простейшего изучения электромагнетизма.

Закон Кулона является основным уравнением электростатики. Этот закон применим в случае неподвижных зарядов и как следствие постоянных (не зависимых от времени) электрических полей.

Закон Кулона в интегральной форме:

Все величины определены в макроскопическом масштабе и макроскопическом объеме.

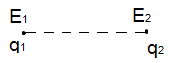
– сила, действующая на единичный заряд со стороны второго заряда в точке 1.

Напряженность электрического поля в точке 1:

В точке 2:

Сила, действующая на единичный положительный заряд, помещенный в точку 1, равна напряженности электрического поля в этой точке, т.е.

Сила, действующая на единичный положительный заряд, помещенный в точку 2, равна напряженности электрического поля в этой точке, т.е.

Сила, действующая на единичный положительный заряд, помещенный в точку , равна напряженности электрического поля в этой точке, т.е. .

Закон Кулона в дифферениальной форме: .

Следовательно, положительные заряды движутся по направлению электрического поля, отрицательные – в противоположномнаправлении.

9;8. Уравнение электростатики и теорема Гаусса – Остроградского

Закон Кулона в интегральной форме: (1)

Закон Кулона в дифферениальной форме: . (2)

Напряженность есть сила , действующая на единичный положительный точечный заряд, помещенный в эту точку.

Переписать ур-е (1) таким образом, чтобы можно было бы решить основную задачу электростатики. Основная задача электростатики состоит в следующем: дано распределение заряда (q, ρ(r), σ(r)), найти распределение электростатического поля.

В векторном анализе Гаусс и Остроградский доказали теорему:

– математическая теорема Г-О.

Правило преобразования поверхностного интеграла к объемному:

S – произвольная замкнутая поверхность,

– векторный элемент площади,

– определенный векторный элемент площади,

,

Применим иатематическую теоремк Г-О к электростатическому полю, вычислив потоквектора напряженности электростатического поля через замкнутую поверхность:

– телесный угол. Полный телесный угол равен 4π, т.е. .

Поток вектора напряженности электростатического поля через полную замкнутую поверхность равняется:

– электростатическая теорема Г-О

Теорема Г-О для электростатического поля: поток вектора напряженности электростатического поля, через замкнутую поверхность численно равен заряду q, заключенного внутри выбранной поверхности, деленному на .

Особенности:

1. 

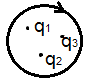
2. Распределенный заряд в объеме

- заряд, заключенный внутри объема V, который ограничен поверхностью.

3. Поверхностно распределенный заряд

, σ – кол-во заряда на единицу поверхности.

Замечание!

1. Теорема Г-О есть следстие з-на Кулона. Физический смысл теоремы Г-О состоит в том, что он выражает з-н Кулона в интегральной форме.

2. Теорема Г-О справедлива для любых полей, у которой любая функция убывает как – кулоновские функции.

3. Если внутри замкнутой поверхности отсутствуют заряды, то поток равен нулю, т.е. Ф=0.

4. Теорема Г-О используется для решения задач электростатики .

Теорему Г-О можно использовать для расчета электростатических полей только в частных случаях, когда известно распределение электростатического поля. В остальных случаях теорема не применима.

5. Теорема Г-О позволяет выявить физический смысл электростатического поля, т.е. электростатическое поле создается электрическими зарядами.