8. Задания к лабораторной работе № 1:

   1. Задания (самостоятельно).Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры (таблица вариантов задания).

а) в строгом смысле; б) в широком смысле.

Таблица. Варианты заданий для выполнения самостоятельной работы

2. Задание для самостоятельной работы. Число х (табл.), все цифры которого верны в строгом смысле, округлить до трех значащих цифр. Для полученного результата вычислить границы абсолютной и относительной погрешностей. В записи числа , указать количество верных цифр по абсолютной и относительной погрешности.

Таблица. Варианты заданий для выполнения самостоятельной работы

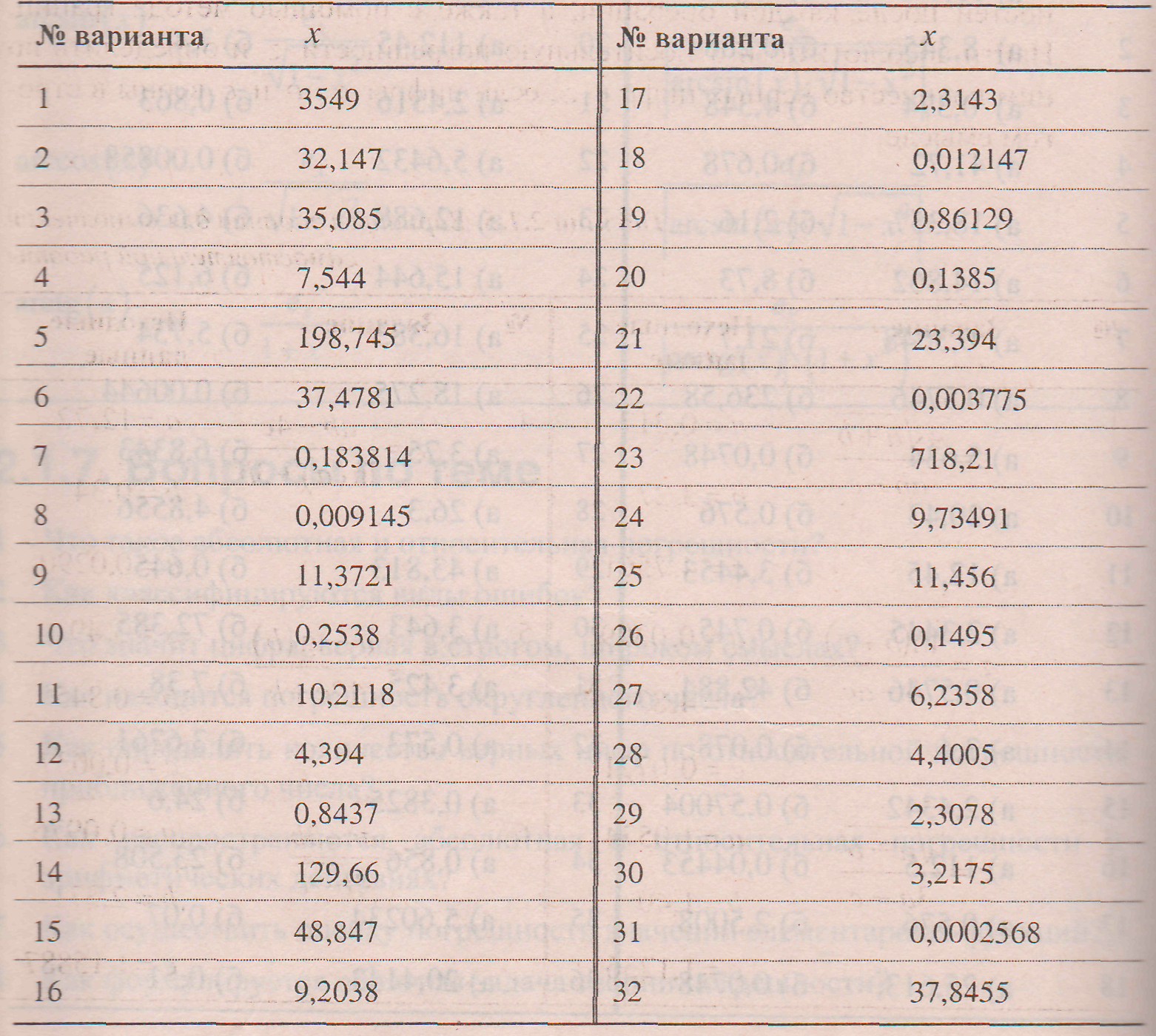
3. Вычислить значение величины z (табл) при заданных значениях чисел а , b и с используя систематический учет абсолютных погрешностей после каждой операции, а также с помощью метода границ. Найти абсолютную и относительную погрешности z и определить по ним количество верных цифр в z, если цифры а , b и с верны в строгом смысле.

Таблица. Варианты заданий для выполнения самостоятельной работы

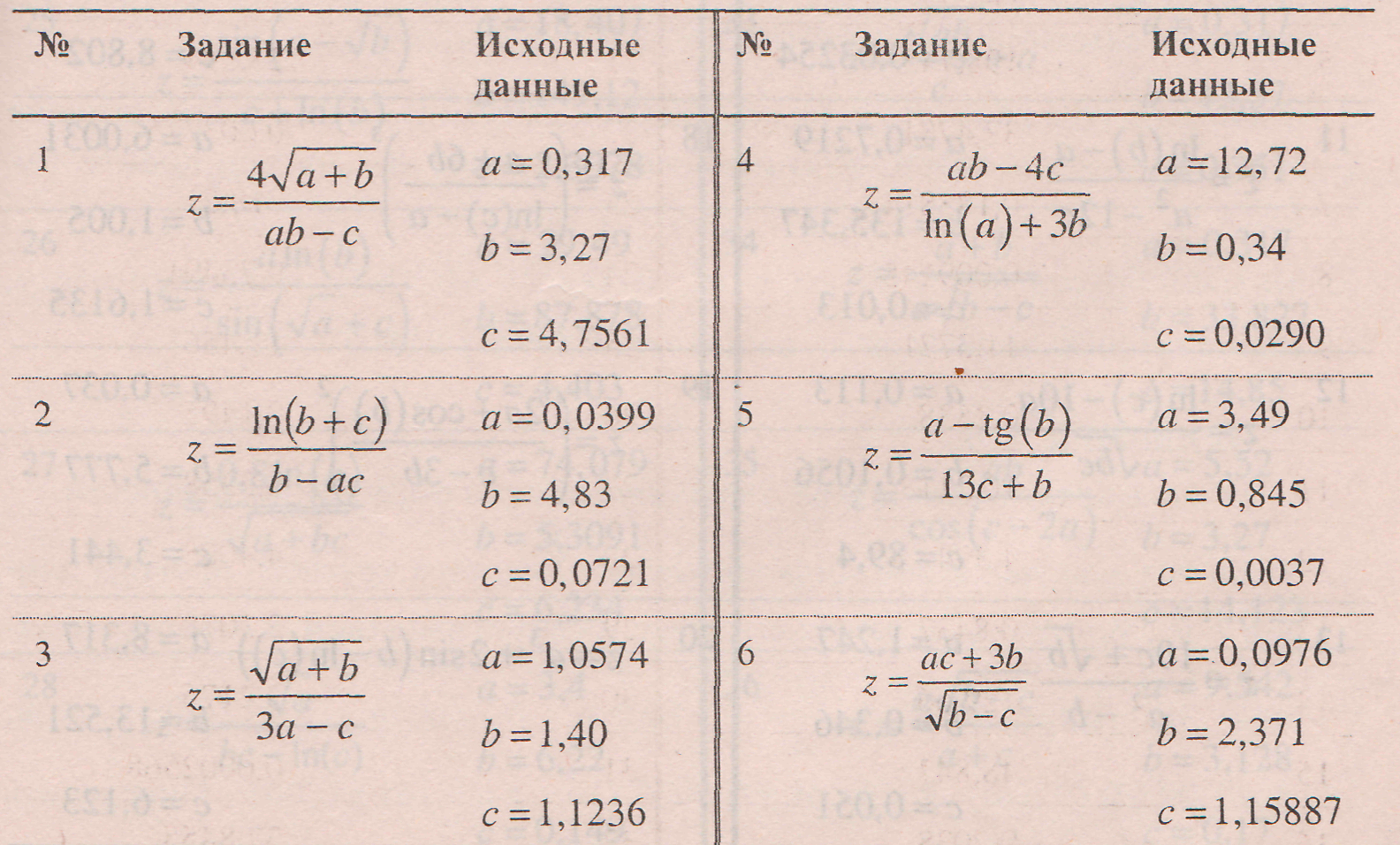
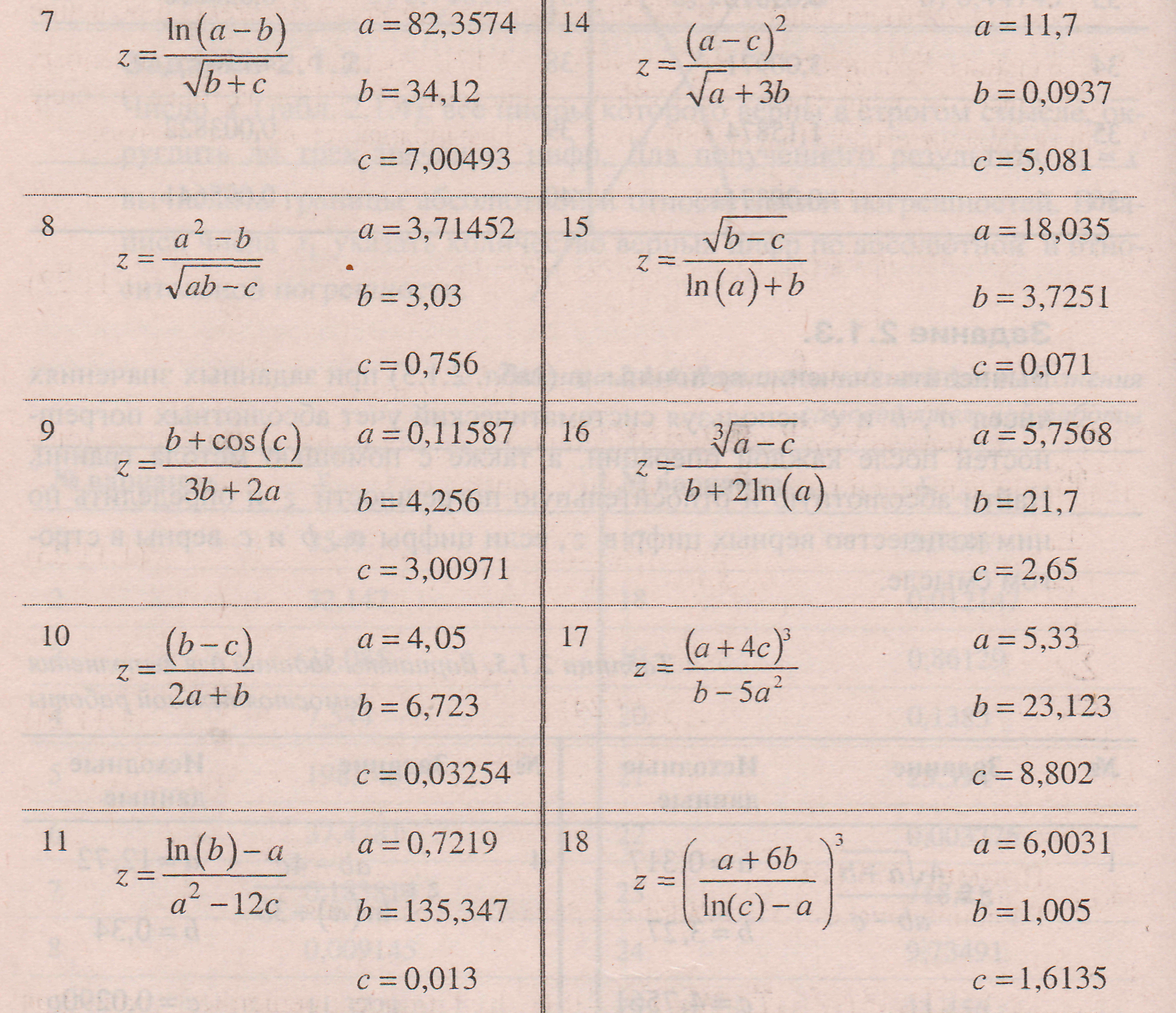
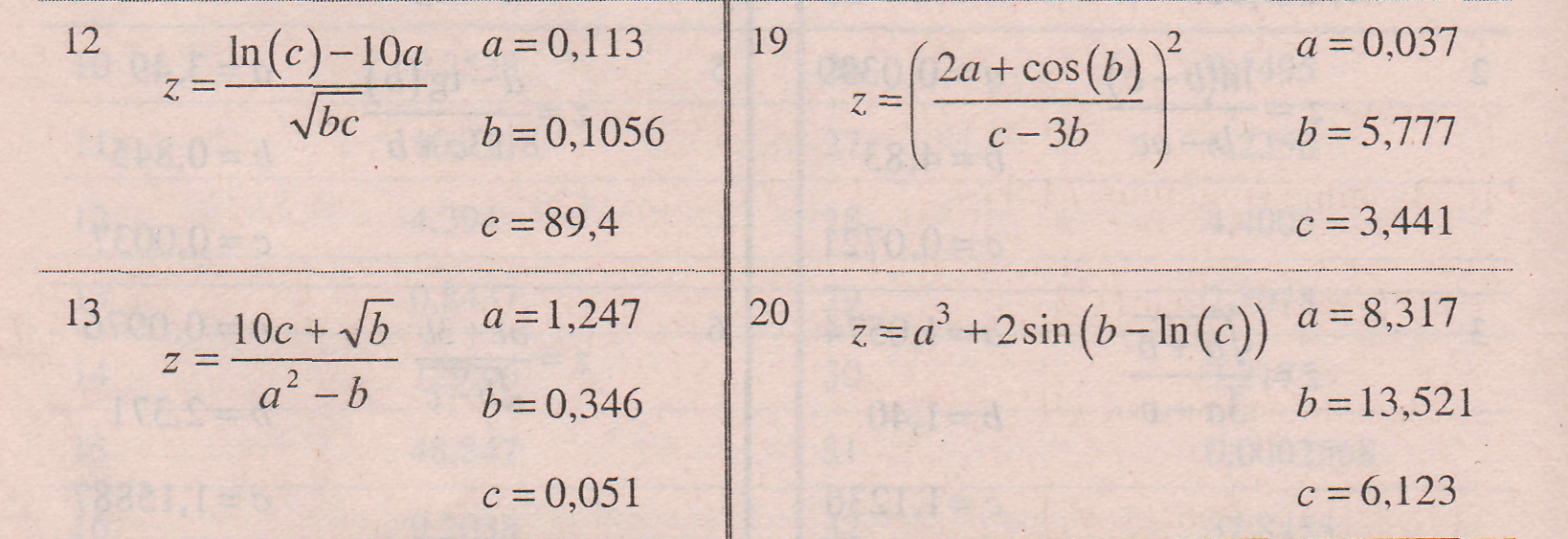
4. Решить следующие задачи, используя метод границ.

   1. Длина воздушной трассы между двумя пунктами равна S км. Самолет преодолевает это расстояние за время t ч. Определить границы средней скорости самолета, если: ; .

   2. Электроплитка рассчитана на напряжение В. Найти сопротивление спирали электроплитки, если известно, что через нее должен пройти ток 5±0,1 А.

   3. Медный брусок имеет объем V м ( ). Найти его массу, если плотность меди кг/м составляет .

5. Решить следующие задачи, используя общую формулу погрешности.

   1. Удельное электрическое сопротивление металла круглого провода длиной l м с поперечным сечением d мм и сопротивлением R Ом определяется по формуле: . Найти , если: l=12,50 ±0,01 м, d=2,00±0,01 мм, R=0,068±0,0005 Ом, =3,141 ±0,001. Определить относительную погрешность .

   2. Вертикальный цилиндрический резервуар наполнен жидкостью. Определить время, необходимое для опорожнения резервуара через круглое отверстие в дне. Диаметр резервуара D=1±0,01м, высота уровня жидкости H=2±0,02м, диаметр отверстия дна d=0,03±0,001м, коэффициент расхода =0,6 ±0,02. Расчет (в секундах) ведется по формуле:

6. Решить следующие задачи, используя обратную задачу теории погрешностей:

   1. С какой точностью надо измерить радиус круга R = 30,5 см и каким количеством значащих цифр следует ограничиться для числа , чтобы площадь круга была известна с точностью до 0,1%?

   2. Длина сторон прямоугольника равны , . Какова допус­тимая предельная абсолютная погрешность при измерении этих величин одинаковая для обеих сторон, чтобы площадь S прямоугольника можно было определить с предельной абсолютной погрешностью ?