Петлевой фазовращатель

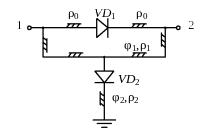
На рис.4 приведена схема петлевого фазовращателя с использованием pin-диодов [1].

Расстояние между точками 1 и 2 много меньше длины волны, поэтому можно считать, что диод VD₁ включен непосредственно между точками 1 и 2. Фазу сигнала определяет длина петли.

Если диоды VD₁ и VD₂ закрыты, то сигнал проходит по петле. Электрическая длина петли φ₁ определяет изменение фазы сигнала при переключении диодов из открытого состояния в закрытое.

Если диоды открыты, сигнал проходит через диод VD₁, и к середине петли подключается короткозамкнутый отрезок с электрической длиной φ₂, чтобы обеспечить бесконечное сопротивление в точках 1 и 2 со стороны петли.

Длину петли фазовращателя можно определить по формуле

, (1)

г

Рис.4.Схема петлевого фазовращателя

де - электрическая длина петли; - постоянная распространения основного типа колебаний в петле фазовращателя, , - длина волны в линии; - длина волны в свободном пространстве.

Электрическую длину отрезка φ₂ можно найти из соотношения

, (2)

где - целое число.

Обычно n = 1. Для этого случая

, (3)

где - постоянная распространения основного типа колебаний в короткозамкнутом шлейфе, , - длина волны в линии.

Из условия обеспечения согласования по входу необходимо, чтобы волновое сопротивление петли равнялось (см. рис.2 и 3) [1]

, (4)

Из следующего выражения определяем :

. (5)

Моделирование петлевого фазовращателя с помощью программы Microwave Office Модель pin-диода

При моделировании используем модель pin-диода PIN2, находящуюся в каталоге элементов в разделе Linear Devices. Вид этой модели приведен на рис.5, а описание входящих в нее элементов - в табл.1.

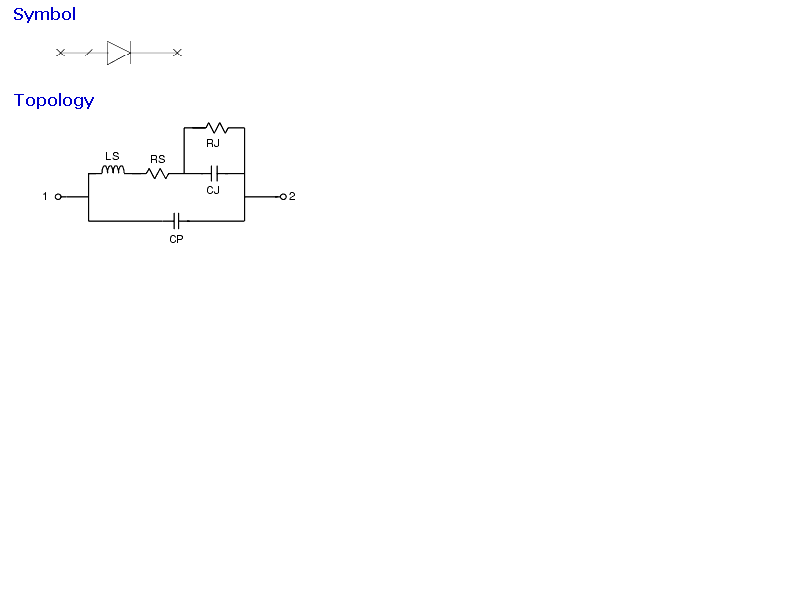
Рис.5. Представление модели pin-диода в виде эквивалентной схемы

Синтаксис уравнений в Microwave Office

Уравнения - это блоки, в которых описаны связи переменных. Переменной является величина, которая может быть числом или любым математическим выражением.

Таблица 1

Параметры эквивалентной схемы pin-диода

Наименование элмента	Описание
CJ	Емкость перехода
RJ	Сопротивление перехода
RS	Последовательное сопртивление; сопротивление потерь
LS	Индуктивность соединения
CP	Емкость корпуса

Уравнения могут быть следующие [2]:

 глобальные;

 встроенные.

Правила записи уравнений

Уравнение содержит имя переменной, расположенное слева от оператора, и математическое выражение, записываемое справа.

Существуют общие правила записи уравнений:

 имя переменной должно состоять из произвольного набора цифр и букв английского алфавита;

 число символов в имени переменной теоретически не ограничено, но длинные имена труднее отображать на экране и в них легче сделать ошибку;

 в имени переменной система различает заглавные и прописные буквы;

 размерность в выражении не пишется, так как она добавляется к переменным автоматически;

 число выражений в тексте теоретически не ограничено;

 при записи уравнений допускается использование математических операторов: сложения (+), вычитания (–), умножения (*), деления (/) и возведения в степень (^).

Синтаксис выражения проверяется согласно алгебраическим правилам. Если выражение неверное, уравнение будет показано зеленым цветом, а ошибки перечислены в окне ошибок.

Перечислим некоторые функции, которые могу использоваться в уравнениях:

 sin(x) - синус x, где x в радианах;

 cos(x) - косинус x, где x в радианах;

 tan(x) - тангенс x, где x в радианах;

 arcsin(x) - арксинус x, где результат в радианах;

 arccos(x) - арккосинус x, где результат в радианах;

 arctan(x) - арктангенс x, где результат в радианах;

 exp(x) - экспонента x;

 log(x) - натуральный логарифм x;

 log10(x) - десятичный логарифм x;

 sqrt(x) - корень квадратный от x;

 stepped(start, stop, step) - определяет диапазон дискретных переменных.

Все аргументы должны быть реальными и скалярными числами.

Программа MWO имеет встроенные глобальные константы: PI (число  = 3,14159...) и j (мнимая единица). Благодаря наличию мнимой единицы имеется возможность записи комплексных чисел, например, выражение Z = 50 – j*1,3 присваивает переменной Z комплексное значение (50 и –1,3).

Программа MWO поддерживает дискретные и непрерывные переменные. Дискретные переменные могут использоваться, только когда позволяется описание дискретными величинами или когда необходимо сохранить переменную, которая округляется до четного числа.

Переменная может быть описана как постоянное число или математическое выражение:

A = 6

Val = x * (4 + y).

Функции могут быть определены, именем переменной со списком аргументов, заключенных в круглые скобки. Следующий пример демонстрирует создание функции, которая имеет два аргумента:

SUM (a, b) = a + b,

Здесь функция SUM суммирует аргументы a и b и присваивает результат переменной b.

Следующее уравнение

c = SUM (–3, 24)

присваивает переменной c значение (–3) + (24).

Можно увидеть результат расчета предварительно определенного уравнения. Результат выражения показывается, когда проект моделируется.

Система уравнений

Val = 5

Val:

Val + 4:

Com (0):

производит следующие вычисления после моделирования:

Val = 5

Val: 5

Val + 4: 9

Com (0): 1

В математических выражениях применяется правило алгебраического старшинства.

Порядок, в котором уравнения размещены на экране, определяет приоритет их вычисления. Переменная, которую необходимо использовать в другом уравнении, должна быть определена заранее.

Порядок приоритета определен следующим образом:

1. уравнения, которые находятся ниже на странице, имеют более высокий приоритет;

2. если два уравнения находятся на одной линии на странице, то вычисление выполняется слева направо.