12. Круглые тела. Цилиндр, конус, шар.

По сравнению с многогранниками круглые тела труд­нее поддаются изображений). Особенно это относится к шару. В самом деле,изображением шара (в ортогональ­ной проекции) будет круг, «увидеть» в котором про­странственное тело при отсутствии каких-то простран­ственных связей нелегко. Поэтому шар, а тем более шары, при решении стереометрических задач обычно не изобра­жают. Скажем даже, что мы не знаем ни одной задачи, в которой фигурирует два или более шаров и в которой хороший чертеж, служащий подспорьем в решении, а не затрудняющий решение, требовал изображения этих ша­ров. С другой стороны, многие задачи на перечисленные в заглавии круглые тела очевидным образом и сразу сводятся к планиметрическим задачам. Так, например, определение радиуса шара, вписанного в заданный конус или описанного около него, сводится к определению ра­диуса окружности, соответственно вписанной в равнобед­ренный треугольник или описанный около этого тре­угольника.

Напомним основные понятия и параметры, связанные с цилиндром. Основные понятия: основание, радиус осно­вания, ось, высота, образующая, осевое сечение, боковая и полная поверхности. Соответственно параметры: радиус основания, площадь основания, высота (равна образую­щей), площадь осевого сечения, площади боковой и пол­ной поверхности, площадь осевого сечения, объем цилинд­ра. Любые два из перечисленных параметров, кроме пары площадь осевого сечение и площадь боковой поверхности, задают цилиндр. X

Для конуса добавляются угловые понятия и соответ­ственно угловые^величины: угол наклона образующей конуса к плоскости основания и угол при вершине осевого сечения, то есть угол между двумя диаметрально противо­положными образующими. Поскольку два указанных угла являются углами равнобедренного треугольника, получа­ющегося в осевом сечении конуса, между ними имеет гаесто очевидная связь. (Какая?) Как и цилиндр, конус задается двумя параметрами, причем имевшее место ог­раничение снимается.

12. Цилиндр и конус имеют равные основания, равные площади полной поверхности и равные объемы. Найти отношение их боковых поверхностей.

Решение: Обозначим радиус основания и высоту ци­линдра через г и Л. По условию радиус основания и высота конуса г и ЗЛ (То, что высота конуса в 3 раза больше высоты цилиндра, следует из равенства площадей оснований и объемов конуса и цилиндра) ГЕсли / — обра­зующая конуса, то 1=~\ г²-\-9h². Боковая и полная по­верхности цилиндра: S_6oKa=2nrh, S_BOAAl=2jir(r+li). Конуса: 5_бокк=лг/, 5_{пол к} =лг(г+/). По условию 5_{пол ц} = =5_П0ЛК, откуда г+2Л = /. Заменяя I через г и Л, после

возведения в квадрат и упрощений, получим h—^-r. Да- лее находим, 1—Щ-г, 5_бокц=-|-лг²,

Збокл^-^-л''²- Отношение равно

12. Образующая конуса наклонена к плоскости осно­вания под углом а. Через вершину конуса проведена плоскость, образующая с плоскостью основания угол р. Найти площадь получившегося сечения, если площадь осевого сечения равна S.

Решение: на рис. 29 а, б и в изображены: общий вид

конуса с проведенными сечениями SBC, осевое сечение и основание конуса. D — середина хорды ВС. По условию ZSDO = p. Пусть /—образующая конуса. Тогда пло­щадь осевого сечения равна -y/²sin(180 —2a)=-|-/²sin 2a.

(3

Рис. 29в

Рис. 296

1 2S

По условию 5=~2-/²sin 2а, Далее,

SO = h = l- sin a, OC = OB = r = l cos а,

OD =SO ctg р = / sin a ctgg,

=-\jOB² — OD²=l Vcos²a — sin²a ctg²^, S_ce4=-LBC.SP — BD'SD

Хл/ cos²a — sin²a cos²<x—sinVctg²^

Полученное выражение можно преобразовать к виду

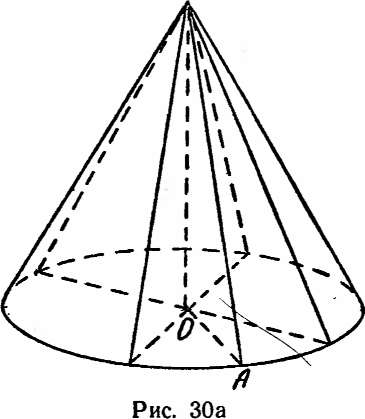
14. (!) Через ось конуса проведены две перпендику­лярные между собой плоскости. Найти радиус шара, вписанного в одну из четырех образовавшихся частей, если радиус основания конуса равен г, а угол наклона образующих к плоскости основания равен а.

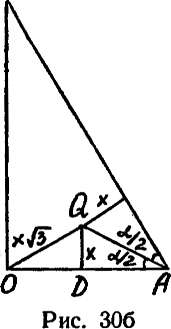
Решение: Если к — радиус искомого шара, то расстоя­ние от его центра до центра основания конуса-равно х-^/З. В самом деле, пусть проведенные плоскости и плоскость основания конуса являются координатными плоскостями (осями являются линии пересечения этих плоскостей). При соответствующем выборе направления осей центр шара Q будет иметь координаты (x_t х, х). Проведем сечение через центр шара и ось конуса (рис. 30 а, б, на рис. 30 б изображен треугольник 50Л, представляющий собой «половину» этого сечения). D — точка касания

шара с плоскостью основания,

S

DA=x ctg-p OD=x^2 Поскольку OD+DA = r, то *(V2 + ctg-f-)=r

Ответ:

15. Полная поверхность конуса в 3 раза больше пло­щади его основания. Найти угол при вершине осевого сечения этого конуса.

Чт)

16. Разверткой боковой поверхности конуса является полукруг, а разверткой боковой поверхности цилиндра является квадрат, равновеликий полукругу. Какое из тел, конус или цилиндр, имеет больший объем и во сколько раз?

Ответ: (

16. В конус, осевое сечение которого—правильный треугольник, вписан шар, а в шар вписан цилиндр, осевое сечение которого квадрат. Найти отношение объемов ко­нуса и цилиндра.

Ответ: (3-^2)

16. Внутри конуса находятся 4 шара одинакового радиуса R, каждый шар касается двух других, основания конуса и его боковой поверхности. Образующая конуса наклонена к плоскости основания под углом а. Найти высоту конуса:

Ответ: tg _a(ctg-|-+V2) )

16. Одна грань куба вписана в основание конуса, а все ребра противоположной грани касаются боковой поверхности этого конуса. Найти объем конуса, если ребро куба равно а.

Ответ: (

16. Ответ

    Найти объем тела, получающегося при вращении единичного квадрата вокруг прямой, проходящей через одну из вершин квадрата, наклоненной к его плоскости под углом а и перпендикулярной диагонали квадрата, не содержащей этой вершины.

Ответ

₍

я cos a \ 3V2 )