11. Многогранники.

При решении стереометрических задач требования к качеству чертежа, его наглядности возрастают по сравне­нию с задачами планиметрическими. Мы не научимся решать сколько-нибудь содержательные стереометричес­кие задачи, если не освоим азбуку построения пространст­венного чертежа. Сюда входит: выбор оптимального поло­жения изображаемого тела (в частности, выбор ориента­ции — верх и низ, право и лево), выбор ракурса и проек­ции, умение минимизировать количество изображенных линий (напомним, что видимые и невидимые линии до­лжны изображаться различным образом), умение строить сечения и проекции на плоскость, умение выделить на пространственном чертеже и соответственно изобразить плоскую конфигурацию, дающую ключ к решению задачи.

Легче всего «поддаются» изображению многогранни­ки, и прежде всего, треугольные и четырехугольные правильные призмы и пирамиды. Выделим два основных типа задач в связи с указанными многогранниками. Пер­вый тип: задачи на вычисление элементов — длин, площа­дей, объемов, линейных и двугранных углов — указанных многогранников. Второй тип: задачи на сечения.

Начнем с задач первого типа.

Перечислим основные элементы правильных призм и пирамид. Линейные: сторона основания, боковое ребро, апофема боковой грани (для пирамид), радиусы окруж­ностей, вписанных или описанных по отношению к основа­нию, радиус описанного около многогранцйка~шара, ради­ус вписанного шара (для призм этот шар не всегда существует) и т. д. Площади: основания (или основа­ний), боковой поверхности, полной поверхности. Объем многогранника. Угловые: линейные углы при вершине, двугранные при основании или между боковыми гранями. Правильная призма или пирамида задается величинами

двух независимых элементов. (В частности эти два эле­мента не могут быть углами.) Таким образом, возникает достаточно обширная серия простейших (почти элемен­тарных) задач: по двум данным величинам найти третью. Например.

1. Найти объем правильной треугольной призмы, полная поверхность которой равна 8д/3, а боковое ребро равно УЗ.

В нарушение нашего принципа при решении этой задачи обойдемся без чертежа. Если а — сторона основа­ния данной призмы, то площадь одного основания будет

^а ^, а полная поверхность ^а + За^З. Получаем для

а уравнение ~^+Зал/3=8->/3, _{из КОТО}р_{ОГО на}йдем а=2.

Объем призмы равен 3.

2. (!) Найти объем правильной четырехугольной пи­рамиды, сторона основания которой равна а, а двугран­ный угол между соседними боковыми гранями равен а.

Решение. На рис. 26 изображена правильная четы­рехугольная пирамида SABCD. Построим линейный угол двугранного угла между соседними боковыми гранями. Для этого опустим из вершин В и D перпендикуляры на ребро SC. Поскольку пирамида правильная, то основани

я

этих перпендикуляров совпадут (точка К). Угол DKB является линейным углом между плоскос­тями SDC и SBC, Z-DKB = (x,.

Рис. 26

С h—SO — OC tg ф (Из прямоу­гольного треугольника SOC), и наконец, находим объем пира­миды.

a

А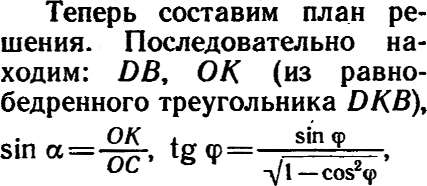

Теперь реализуем этот план:

DB — a-\f2,

ОК=ОВ ctgf=a^fctgf, sin a=-~~=ctg-|-

,* ^a

tg<p:

r- co:

•cos a

a³V2 cos

Ответ:

6-v— c°s a

(Обращаем внимание, должно быть

a> 90°).

3. (!) Найти радиус вписанного и радиус описанного шара для треугольной пирамиды со стороной основания а и высотой h.

Решение. Пусть О — центр основания ABC правильной треу­гольной пирамиды SABC, М — середина ВС (рис. 27а). AM — высота в треугольнике ABC,

ОМОчевидно,

о о

что центры обоих шаров находят­ся на прямой SO. Найдем снача­ла радиус описанного шара. Для этого продолжим SO до пе­ресечения с описанным шаром в точке D. (рис. 276). Очевид­но, SD — диаметр этого шара, Z-SAD=90°. В прямоугольном треугольнике SAD известны вы­сота АО, опущенная на гипотенузу, и отрезок гипотенузы

.ДО² а²

SO. Из формул задачи № 14 найдем OD =-—=—-.

и(/ o/i

Таким образом, если R — радиус описанного шара, то

2R=SD=SO+OD=h+4r=^^--

on on

Для нахождения г — радиуса впиранного шара рас­смотрим треугольник SOM (рис. 27в). Если Q — центр вписанного шара, то QM — биссектриса угла SMO и QO—r. В прямоугольном треугольнике SMO известны

Рис. 27а

катеты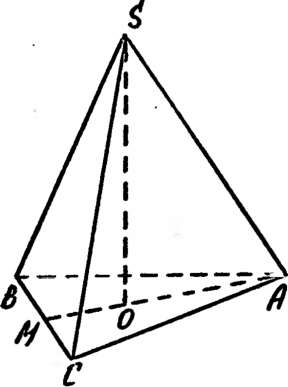

SO=h и ОМ=-^~. Находим

о

гипотенузу

SM—-y Н²-\——. По теореме о биссектрисе внутреннего угла (задача № 49) имее

м

г ал/3 ah ^L—— —=г, откуда г—

h—r

л²+—— ^ 12

Ответ: радиус описанного шара равен

ah

вписанного шара равен - .

Уже на этих примерах, особенно на последнем, мы видим, что решение планиметрических задач очень часто (практически, всегда), сводится к решению одной или нескольких планиметрических задач.

Рис. 27в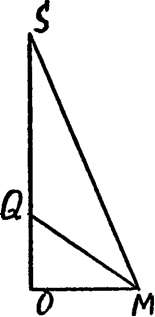

Следующий тип задач — задачи на сечения. В основе этих задач лежит умение построить сечение многогранни-

Рис. 276

ка плоскостью и определить вид этого сечения. Здесь мы рассмотрим лишь задачи, в которых сечение задано или тремя точками, или двумя точками и прямой, параллель­ной плоскости сечения, или точкой и прямой, или двумя пересекающимися (параллельными) прямыми, или точкой и параллельной плоскостью. В принципе возможны и нередко встречаются задачи, в которых сечение задано иным, более «хитрым» способом.

4. (!) Построить сечение куба плоскостью, проходя­щей через середины двух смежных ребер куба и наиболее удаленную от соединяющей их прямой вершину куба.

Найти площадь этого сечения, если ребро куба равно 1.

®Л/

З/t'+a²

6/г

радиус

Основная схема, которой обычно следует придержи­ваться при построении сечения, состоит в последователь­ном построении прямых, по которым плоскость сечения

пересекается с плоскостя­ми граней данного много­гранника или же с каки­ми-то вспомогательными плоскостями.

Пусть К и L — середи­ны ребер D\C\ и С\В\ куба ABCDAyB_xCi D, (рис. 28). Наиболее удаленной от прямой KL вершиной яв­ляется очевидно вершина А. Плоскость сечения пе­ресекается с плоскостью A\B\C\D\ по прямой KL. Продолжим KL до пересе­чения с прямыми A\D\ и А\В\ в точках Е и F. (В этом продолжении — все дело. Прием этот стандартный. За­помните его.) Точка Е принадлежит плоскости ADD\A\. В этой же плоскости расположена еще одна точка наше­го сечения — точка А. Следовательно, плоскость сечения пересекается с плоскостью ADD\A\ по прямой АЕ. Обо­значим через N — точку пересечения этой прямой с реб­ром DD\. Вновь имеем в плоскости грани, на сей раз грани DCC\D\, две точки, принадлежащие нашему сече­нию,— К и N. Строим отрезок KN, являющийся стороной многоугольника сечения. Аналогично находится точка М. Окончательно получаем, что нашим сечением является пятиугольник KLMAN. Найдем его площадь. Эту пло­щадь можно представить в виде разности площадей: из площади треугольника AEF вычитаются площади двух, очевидно равных, треугольников NKE и MLF. Более того, два последних треугольника подобны треугольнику AEF

1 / ЕК LF 1 \ с коэффициентом ~ ( Значит, их площа­

ди в 9 раз меньше площади треугольника AEF, а площадь искомого пятиугольника составляет ⁷/_э площади треу­гольника AEF. Осталось найти площадь треугольника AEF. Последовательно найдем: D\E=D\K = B\L = B\F=

~ 2 '

Рис. 28

Таким образом AEF — равнобедренный треугольник с ос­

нованием EF=-~->j2 и боковыми сторонами AE=AF=^~. Его площадь равна

Ответ: площадь сечения равна

(Чтобы не удлинять наше решение, мы опустили мно­гие элементы полного обоснования. Например, почему треугольники ENK и EAF подобны).

5. Найти объем правильной треугольной пирамиды, боковое ребро которой равно 3, а полная поверхность 9-\/3.

Ответ

6. В правильной четырехугольной пирамиде противо­положные боковые грани попарно перпендикулярны. Най­ти плоские углы при вершине, в которой сходятся боковые ребра.

Ответ: (Arccos-^-).

6. В правильной четырехугольной пирамиде центр

описанного шара принадлежит плоскости основания. Во

сколько раз радиус вписанного шара меньше радиуса

описанного шара? ₍ & ^ ,

Ответ: ( +

6. В основании треугольной призмы лежит правиль­ный треугольник. Известно, что существует шар, вписан­ный в эту призму, и шар, около нее описанный. Найти отношение радиусов этих шаров.

Ответ: (JL).

6. Все ребра правильной треугольной призмы АВСА\В\С\ равны 1. Найти площадь сечения этой призмы плоскостью, проходящей через середины ребер АА\, А\В\ и АС.

Ответ:

6. Найти объем многогранника ABCDKL, в котором ABCD прямоугольник .со сторонами аи В, KL параллель­на АВ, удалена от плоскости ABCD на расстояние h и равна с.

Ответ: (

И. Доказать, что если какая-то высота пирамиды проходит через точку пересечения высот противополож­ной грани, то и любая другая высота обладает этим же свойством.

(Докажите, что из условия следует попарная перпендикулярность противоположных ребер, а из попарной перпендикулярности ребер следу­ет, что любая высота пирамиды проходит через точку пересечения высот соответствующей гра­ни.)