8. Четырехугольники.

В школьном курсе изучаются следующие четырех­угольники специального вида: трапеция, параллелограмм, ромб, прямоугольник, квадрат. (К этому списку можно добавить вписанные и описанные четырехугольники). Бу­дем считать, что параллелограмм не является частным случаем трапеции. В большинстве случа­ев это удобнее. Сформулируем и докажем несколько теорем, при­мыкающих к школьному курсу, полезных при решении задач.

74. (!) Если d\ и d.2 диагона­ли четырехугольника, <р — угол между диагоналями, S — его

площадь, то S—-^-d\d2 sin <p

Иными словами: площадь произвольного четырехугольни­ка, в том числе и невыпуклого равна полупроизведению его диагоналей и синуса угла между ними.

В известном смысле теорема 74 представляет собой обобщение формулы для площади треугольника:

S—^ab sin С Доказывается она достаточно просто.

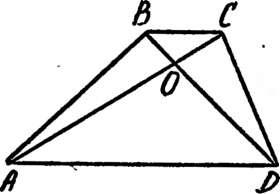
Пусть О — точка пересечения диагоналей четырехуголь­ника ABCD (рис. 16). Высота, опущенная на сторону BD в треугольнике BCD равна ОС -sin <р, а в треугольнике ABD она равна ОЛ • sin <р. Таким образом,

5=S_BCD+S_ABD=±BD • ОС • sin q>+4~^BD '^0А'^sin Ф= =-уВ£(ОС+ОЛ) sin <p=-i-££).4C.sin sin <p.

Полезно запомнить следующее свойство трапеции.

75. (!) Пусть ABCD тра­пеция с основаниями AD и ВС, О — точка пересечения ее диа'- гоналей. Тогда треугольники АВО и CDO — равновелики.

( SABO"**¹ SCDo)'

Пусть ABCD — четыреху­гольник. Тогда обратно, из рав- р_ис 17 новеликости треугольников АВО

и CDO следует параллельность

AD и ВС.

Доказательство. Из параллельности AD и ВС следу­ет равновеликость треугольников ABD и ACD (рис. 17), из равновеликости треугольников ABD и ACD следует равновеликость треугольников АВО и CDO (AD || BCoS_ABD=S^^-^S^bo=S_CDO). Прослеживая эту цепочку в обратном направлении, докажем обратное утверждение.

Кстати, в задачах про трапеции очень часто бывает

полезно продолжить до пе­ресечения ее боковые сторо­ны (см. задачу № 78). Из формулы, выражающей длину медианы через сторо­ны треугольника (задача № 12), следует следующее свойство параллелограмма. 76. (!) Сумма квадра- р_ис is тов сторон параллелограм­

ма равна сумме квадратов

его диагоналей.

В самом деле, если О — точка пересечения диагоналей

параллелограмма ABCD (рис. 18), то BO=-^-BD — ме­диана в треугольнике ЛВС. Значит, 4В0²=2ЛВ²-+-

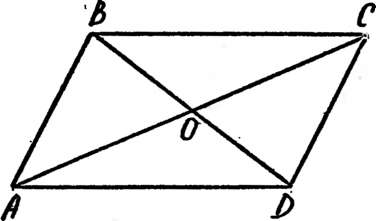
+2ВС²- АС², откуда ЛС^е+BD²=2AB²+2 ВС²

Довольно часто встречаются задачи, в которых ис­пользуется следующее свойство произвольного четырех­угольника.

77. (!) Середины сторон произвольного четырехуголь­ника служат вершинами параллелограмма. Стороны этого параллелограмма соответственно параллельны диагона­лям четырехугольника и равны половинам этих диаго­налей.

Утверждение этой задачи является следствием свойств средней линии треугольника.

Решите теперь следующие задачи.

77. Найти площадь трапеции, основания которой рав­ны 2 и 1, а углы, прилегающие к большему основанию, равны 30° и 60°.

Ответ: ( М.)

77. Пусть а и b — основания трапеции. Доказать, что отрезок, соединяющий середины ее диагоналей равен

iia-bi

77. На сторонах А В и AD параллелограмма ABCD взяты точки М и N так, что Найти пло­щадь четырехугольника AMCN, если площадь паралле­лограмма равна 6.

Ответ: (2)

77. ABCD — прямоугольник, в котором АВ= 1, ВС = 2. На сторонах ВС и DA взяты точки М и N так, что BMDN — ромб. Найти сторону ромба.

Ответ: ^

77. Площадь трапеции равна 3, основания 1 и 2. Найти площади треугольников, на которые трапеция раз­делена диагоналями.

Ответ: (-i* А ±) V з' з' з' з /

77. Доказать, что площадь параллелограмма с верши­нами в серединах сторон данного четырехугольника равна половине площади этого четырехугольника.

78. Доказать, что если отрезки, соединяющие середи­ны сторон данного четырехугольника

а) равны, то диагонали четырехугольника перпенди­кулярны;

б) перпендикулярны, то диагонали четырехугольника равны.

77. Пусть Af — середина стороны ВС параллелограм­ма ABCD, N — точка на стороне AD такая, что AN—2ND В каком отношении отрезок MN делит диагональ АС?

Ответ: (4:3)

77. Найти отношение оснований трапеции, если из­вестно, что средняя линия делится диагоналями на 3 равные части.

Ответ: (2:1)

77. Найти площадь параллелограмма, стороны кото­рого равны а и Ь_у а угол между диагоналями равен^а.

Ответ: —6²|tg а