8.7. Схема исследования функций и построения графиков.

Сведём рассмотренные в этом разделе отдельные элементы в один алгоритм, с помощью которого исследуются функции и строятся их графики.

1. Общий характер функции:

• область определения функции и, если это возможно, область её значений;

• наличие чётности, периодичности;

• нахождение, если это возможно, пересечений графика функции с осями координат и областей её знакопостоянства (граничными точками интервалов знакопостоянства могут быть только концы интервалов области определения, точки разрыва, нули функции);

• область непрерывности функции, её разрывы и их характер;

• пределы при стремлении к границам области определения (при этом будут получены уравнения горизонтальных и вертикальных асимптот, если они есть);

• наличие наклонных асимптот.

II. Исследование функции с помощью первой производной на экстремумы и участки монотонности. Граничными точками интервалов монотонности функции могут быть только концы интервалов области её определения, точки разрыва, критические точки первого рода.

3. Исследование функции с помощью второй производной на выпуклость и точки перегиба. Граничными точками интервалов выпуклости графика функции могут быть только концы интервалов области её определения, точки разрыва, критические точки второго рода.

После первого этапа исследования полезно построить примерный график, который уточняется в результате второго и третьего этапов.

Примеры:

1. .

I. ; общего вида; непериодична; при ;

; ; ; ; точка - точка разрыва второго рода; прямая - вертикальная асимптота. Ищем наклонные асимптоты: ; ; прямая - двусторонняя наклонная асимптота. Интервалы знакопостоянства функции:

II.

. Критические точки первого рода: , . Определяем интервалы монотонности (в таблицу включаем концы интервалов области определения и критические точки):

	+	0				0	+
		Мax=0		Не опред.		Min=

III.

Критические точки второго рода: , . Определяем интервалы выпуклости графика:

	+	0		0			+
		Точка перегиба		Нет перегиба		Не опред.

Г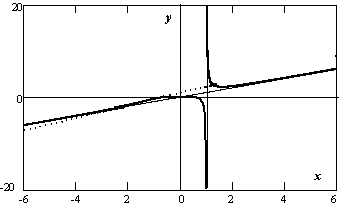 рафик функции приведён на рисунке справа.

2. .

I. ; общего вида; непериодична. ; ;

; . Точка - точка разрыва второго рода; прямая - вертикальная асимптота. Так как функция не определена при , ищем только правую наклонную асимптоту: , , наклонной асимптоты нет. Функция принимает отрицательные значения на интервале , положительные значения на интервале .

II. , единственная стационарная точка - . Интервалы монотонности:

				0	+
		Не опред.		Min=

III. , - критическая точка второго рода. Интервалы выпуклости:

			+	0	
		Не опред.		Точка перегиба

Г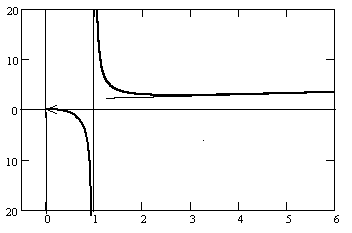 рафик функции приведён на рисунке справа

3. .

I. ; общего вида; непериодична; при и ; ; . Находим и : ; , асимптот нет. Первый эскиз графика функции приведён справа.

I I. , критические точки первого рода , . Таблица изменения знаков производной:

			+	0	
		Мin=0		Mах=1

О тмечаем, что первый эскиз неправильно описывает поведение функции в окрестности точки 0.

III. . для , выпуклость графика направлена вверх, точек перегиба нет.

Окончательный вариант графика:

4. .

I. ; общего вида; периодична, период Т=2 , поэтому достаточно построить функцию на одном периоде, например, на . Находим значения функции на концах этого отрезка: . При ; найдём нули функции:

На отрезке расположены два нуля функции: и . на интервалах и , на интервале . В силу периодичности функции нет необходимости искать пределы функции на бесконечности и асимптоты.

II. . Ищем критические точки первого рода: при и , на отрезке находятся три таких точки: , и . Характер критических точек определяем с помощью второй производной:

; , , ; точка - точка максимума с , точка - точка минимума с . Для определения характера точки найдём , . Первая отличная от нуля производная в точке имеет нечётный порядок, т.е. в этой точке экстремума нет. Всю информацию отражаем на эскизе графика.

III. Находим критические точки второго рода: , на отрезке находятся четыре точки, удовлетворяющие этим уравнениям (в порядке возрастания): , , , . Каждая из этих точек является точкой перегиба, так как вторая производная меняет знак при переходе через к аждый свой нуль. Эти точки разбивают отрезок на пять подмножеств; мы уже определяли знак второй производной в точке , принадлежащей четвёртому подмножеству, и в точке , принадлежащей пятому подмножеству, по этой информации без труда определяются направления выпуклости графика функции на каждом из пяти интервалов. Окончательный график функции на отрезке :

5. .

1. ; общего вида; непериодична; непрерывна; при и ; отрицательна на интервале и положительна вне этого интервала; , следовательно, график функции имеет горизонтальную асимптоту .

2. при ; , .

	+	0		0	+
		Мax		Min

; .

III.

при , , , каждая из этих точек – абсцисса точки перегиба. Распределение знаков второй производной очевидно: +  + . Окончательный график функции:

6. .

I. ; общего вида; непериодична; при ; пределы на границах области определения: , , ,

; - точка разрыва второго рода; прямая - вертикальная асимптота. Ищем наклонные асимптоты: ,

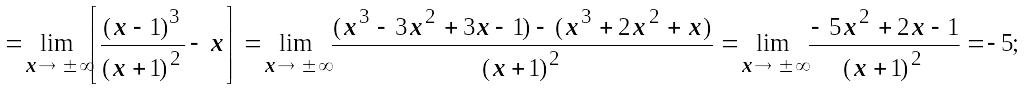
прямая - наклонная асимптота при .

2. .

В таблицу для определения знаков производной включаем внутреннюю границу области определения:

	+	0			+	0	+
		Мax = = -13.5		Не определ.		Нет экстр.

I II. Единственная точка перегиба – точка с абсциссой , при выпуклость графика направлена вверх, при - вниз. График функции:

7. ( ).

1. ; общего вида; непериодична; на ;пределы на границах области определения: , , , ; прямая - вертикальная асимптота. Ищем наклонные асимптоты: . Необходимо рассмотреть случаи и порознь. При ,

Прямая - наклонная асимптота при .

При ,

Прямая - наклонная асимптота при .

II.

Критическая точка первого рода - . Производная обращается в нуль ещё в точке , но это - краевая точка области определения, в таблицу для исследования знаков производных она войдёт именно как краевая точка.

		0		0	+
		0		Min=

III.

Вторая производная всегда положительна, график функции (справа) имеет выпуклость, направленную вниз.

8. .

I. общего вида; непериодична; непрерывна и неотрицательна на ; пределы на границах области определения: , , - вертикальная асимптота. Наклонные и горизонтальные асимптоты не ищем, так как область определения ограничена. Заметим, что .

II. на всей области определения, так что функция монотонно убывает.

III. обращается в нуль (первая скобка всегда положительна, так как ) только при , это единственная точка перегиба. График: