
- •6. Дифференцируемость функций.
- •6.1. Определение производной функции.
- •6.1.1. Задачи, приводящие к понятию производной.
- •6.1.1.2. Нахождение углового коэффициента касательной к графику функции.
- •6.1.2. Определение производной.
- •6.1.3. Геометрический смысл производной. Уравнения касательной и нормали к графику гладкой функции.
- •6.2. Производные некоторых элементарных функций.
- •6.3. Производная обратной функции.
- •6.4. Формула для приращения функции, имеющей производную.
- •6.5. Основные правила дифференцирования.
- •6.6. Примеры вычисления производной.
- •6.7. Односторонние и бесконечные производные.
- •6.8. Дифференцируемость функций. Дифференциал.
- •6.9. Таблица производных и дифференциалов.
- •6.10. Производные функций, заданных параметрически и неявно.
- •6.11. Производные и дифференциалы высших порядков.
- •7. Основные теоремы дифференциального исчисления.
- •7.1. Теорема Ферма.
- •7.1.1. Определение экстремума функции.
- •7.2. Теорема Ролля.
- •7.3. Теорема Лагранжа.
- •7.4. Теорема Коши.
- •7.5. Теоремы Лопиталя.
- •7.6. Раскрытие неопределённостей с помощью правила Лопиталя.
- •7.7. Формула Тейлора.
- •7.7.3. Форма Пеано остаточного члена формулы Тейлора.
- •7.8. Представление по формуле Маклорена
- •7.9. Применение формулы Тейлора для нахождения пределов
- •8. Исследование функций и построение их графиков.
- •8.1. Условие постоянства функции.
- •8.2. Условия монотонности функции.
- •8.3. Экстремумы функции, необходимое условие.
- •8.4. Достаточные условия экстремума функции.
- •8 .5. Выпуклость графика функции. Точки перегиба.
- •8.5.1. Направление выпуклости графика функции.
- •8.6. Асимптоты графика функции.
- •8.7. Схема исследования функций и построения графиков.
8.4. Достаточные условия экстремума функции.
8.4.1.
Первый достаточный признак экстремума
(в критической точке, по знаку первой
производной).
Пусть точка
- критическая точка первого рода функции
,
т.е. функция имеет производную в каждой
точке некоторой проколотой окрестности
![]() точки
,
и пусть
точки
,
и пусть
![]() сохраняет определённый знак как справа,
так и слева от точки
(в отдельности). Тогда: если производная
сохраняет знак при переходе через точку
,
то экстремум в этой точке отсутствует;
если производная меняет знак при переходе
через точку
,
то точка
- точка экстремума, при этом если
>0
при x<
,
<0
при x>
,
то
- точка максимума, если
<0
при x<
,
>0
при x>
,
то
- точка минимума.
сохраняет определённый знак как справа,
так и слева от точки
(в отдельности). Тогда: если производная
сохраняет знак при переходе через точку
,
то экстремум в этой точке отсутствует;
если производная меняет знак при переходе
через точку
,
то точка
- точка экстремума, при этом если
>0
при x<
,
<0
при x>
,
то
- точка максимума, если
<0
при x<
,
>0
при x>
,
то
- точка минимума.

 Док-во.
Пусть и
сохраняет знак при переходе через
критическую точку
,
примем для определённости, что
>0
при
Док-во.
Пусть и
сохраняет знак при переходе через
критическую точку
,
примем для определённости, что
>0
при
![]() .
Это означает, по теор.7.1.2
о связи знака производной с возрастанием
и убыванием функции,
что функция возрастает как справа, так
и слева от точки
,
т.е. экстремум в этой точке отсутствует.
Аналогично, если
<0
для
,
то
убывает как слева, так и справа от точки
,
т.е. экстремум в этой точке отсутствует.
.
Это означает, по теор.7.1.2
о связи знака производной с возрастанием
и убыванием функции,
что функция возрастает как справа, так
и слева от точки
,
т.е. экстремум в этой точке отсутствует.
Аналогично, если
<0
для
,
то
убывает как слева, так и справа от точки
,
т.е. экстремум в этой точке отсутствует.
Рассмотрим теперь случай, когда производная меняет знак при переходе через точку ; пусть, для определённости, >0 при x< , <0 при x> , т.е. производная меняет знак с "+" на "-". По той же теореме 7.1.2 в этом случае возрастает при x< и убывает при x> , т.е. - точка максимума.
Совершенно аналогично, в случае, когда производная меняет знак с "-" на "+" при переходе через точку , получим, что - точка минимума.
Рассмотрим два примера на применение изложенного алгоритма нахождения экстремумов.
Найти участки монотонности и экстремумы функции
 .
.
Производная этой функции существует везде:
![]() ,
поэтому критические точки 1-го рода
совпадают со стационарными точками:
,
поэтому критические точки 1-го рода
совпадают со стационарными точками:
![]() ,
,
![]() ,
,
![]() .
Эти точки разбивают область определения
(всю числовую ось) на четыре интервала,
в каждом из которых производная сохраняет
знак, т.е. функция сохраняет направление
монотонности. Составим таблицу:
.
Эти точки разбивают область определения
(всю числовую ось) на четыре интервала,
в каждом из которых производная сохраняет
знак, т.е. функция сохраняет направление
монотонности. Составим таблицу:
|
|
|
|
|
|
|
|
|
+ |
0 |
|
0 |
+ |
0 |
+ |
|
|
Мах=0 |
|
min |
|
Нет экстр. |
|
Т очка
- точка максимума,
очка
- точка максимума,
![]() ;
точка
-
точка минимума,
;
точка
-
точка минимума,
![]() ;
в точке
экстремума нет (функция возрастает в
окрестности этой точки). График функции
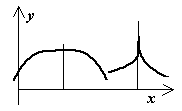
на отрезке [-2.5, 2] приведён справа.
;
в точке
экстремума нет (функция возрастает в
окрестности этой точки). График функции
на отрезке [-2.5, 2] приведён справа.
2.
Найти участки монотонности и экстремумы
функции
![]() .
.
![]() .
Решая уравнение
.
Решая уравнение
![]() ,
находим стационарные точки
,
находим стационарные точки
![]() ,
другими критическими точками первого
рода будут точки
,
,
другими критическими точками первого
рода будут точки
,
![]() ,
в которых знаменатель обращается в
нуль. Так как функция чётна, достаточно
исследовать её поведение при
,
в которых знаменатель обращается в
нуль. Так как функция чётна, достаточно
исследовать её поведение при
![]() ;
в таблицу включаем левую окрестность
точки
:
;
в таблицу включаем левую окрестность
точки
:
|
|
|
|
|
|
|
|
|
|
|
+ |
0 |
|
|
|
|
|
Мin=0 |
|
Max |
|
Нет экстр. |
|
Т очка
очка
![]() ,
как и точка
,
будет точкой максимума с тем же значением
функции; в точке
,
как и точка
,
будет точкой максимума с тем же значением
функции; в точке
![]() экстремум отсутствует.
экстремум отсутствует.
8.4.2.
Второй достаточный признак экстремума
(в стационарной точке, по знаку второй
производной).
Пусть функция
в стационарной точке
имеет
не только первую, но и вторую производную.
Тогда если
![]() ,
то
- точка минимума, если
,
то
- точка минимума, если
![]() ,
то
- точка максимума.
,
то
- точка максимума.
Это
правило непосредственно следует из
теоремы 7.1.2
о связи знака производной с возрастанием
и убыванием функции
и из первого
достаточного признака экстремума 8.4.1:
если
- стационарная точка (![]() ),
и
,
то производная
возрастает в точке
.
Так как
,
то
отрицательна при
и положительна при
в некоторой окрестности точки
,
т.е.
меняет
знак с "-" на "+" при переходе
через критическую точку
,
следовательно,
- точка минимума. Если
- стационарная точка, и
,
то совершенно также доказывается, что
- точка максимума.
),
и
,
то производная
возрастает в точке
.
Так как
,
то
отрицательна при
и положительна при
в некоторой окрестности точки
,
т.е.
меняет
знак с "-" на "+" при переходе
через критическую точку
,
следовательно,
- точка минимума. Если
- стационарная точка, и
,
то совершенно также доказывается, что
- точка максимума.
8.4.3.
Третий достаточный признак экстремума
(в стационарной точке, по старшим
производным).
Мы получили уже два достаточных признака
наличия экстремума функции в точке, но
даже с их помощью затруднительно ответить
на вопрос: имеет ли функция
![]() экстремум в точке
экстремум в точке
![]() ?
И первая, и вторая производные функции
в этой точке равны нулю; исследовать
знак первой производной в окрестности
точки
непросто. Ответ на этот вопрос даёт
следующее правило: пусть функция
имеет в точке
все производные вплоть до n-го
порядка, причём
?
И первая, и вторая производные функции
в этой точке равны нулю; исследовать
знак первой производной в окрестности
точки
непросто. Ответ на этот вопрос даёт
следующее правило: пусть функция
имеет в точке
все производные вплоть до n-го
порядка, причём
![]()
![]() .
Тогда, если n
(порядок первой отличной от нуля
производной) нечётно, то экстремум в
точке
отсутствует; если
n
чётно, то при
.
Тогда, если n
(порядок первой отличной от нуля
производной) нечётно, то экстремум в
точке
отсутствует; если
n
чётно, то при
![]() - точка минимума, при
- точка минимума, при
![]() - точка максимума.
- точка максимума.
Док-во. При сделанных предположениях относительно производных функции её разложение в ряд Тейлора с остаточным членом в форме Пеано имеет вид
![]()
![]() ,
где
,
где
![]() при
.
При х,
достаточно близких к
,
знак последнего выражения определяется
знаком
при
.
При х,
достаточно близких к
,
знак последнего выражения определяется
знаком
![]() .
Если n
нечётно, то разность
.
Если n
нечётно, то разность
![]() меняет знак при переходе через точку
,
т.е. экстремум отсутствует. Если n
чётно, то эта разность сохраняет знак
при переходе через точку
,
при этом если
,
то эта разность отрицательна, т.е.
- точка максимума, если
,
то эта разность положительна, т.е.
- точка минимума.
меняет знак при переходе через точку
,
т.е. экстремум отсутствует. Если n
чётно, то эта разность сохраняет знак
при переходе через точку
,
при этом если
,
то эта разность отрицательна, т.е.
- точка максимума, если
,
то эта разность положительна, т.е.
- точка минимума.
Для
функции
получим:
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
порядок первой отличной от нуля
производной нечётен, следовательно,
эта функция экстремума в точке 0 не
имеет.
;
порядок первой отличной от нуля
производной нечётен, следовательно,
эта функция экстремума в точке 0 не
имеет.








