5.4.2. Классификация точек разрыва.

Изложенное выше сводится к следующему: для того, чтобы функция f(x) была непрерывной во внутренней точке х₀ области определения, необходимо и достаточно выполнение четырёх условий: 1. f(x) определена в точке х₀ (т.е.  f(х₀)) и некоторой её окрестности;

2.  ; 3.  ;

4. Все эти три числа равны между собой: (в правом и левом концах области определения снимаются условия, относящиеся, соответственно, к пределам справа и слева).

Опр.5.1.10. Если хотя бы одно из перечисленных условий непрерывности функции в точке не выполняется, f(x) называется разрывной в точке х₀, а сама точка х₀ называется точкой разрыва функции f(x).

Рассмотрим возможные варианты:

Опр.5.1.11. Точка разрыва х₀ называется точкой устранимого разрыва, если существуют односторонние пределы и они равны между собой (т.е.  ).

И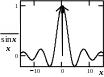 з этого определения следует, что точка разрыва х₀ может быть точкой устранимого разрыва только в случае, когда значение f(x) в точке х₀ либо не определено, либо не равно .

Пример:

. Эта функция не определена в точке х₀ = 0, но   существуют односторонние пределы, и они равны. Следовательно, точка х₀ = 0 - точка устранимого разрыва. Если доопределить функцию в этой точке: то будет получена непрерывная в точке х₀ = 0 функция, таким образом, разрыв будет "устранён".

Опр.5.1.12. Точка разрыва х₀ называется точкой разрыва первого рода (иногда применяется термин "скачок"), если существуют односторонние пределы , но они не равны между собой.

П ример:

(сигнум, "знак-функция"). При х+0 у(х)1 (справа от точки 0 у(х)=const=1); при х-0 у(х)-1, у(х+0) и у(х-0) существуют и не равныточка х₀ = 0 - точка разрыва первого рода.

Опр.5.1.13. Точка разрыва х₀ называется точкой разрыва второго рода, если хотя бы один из односторонних пределов не существует ( в частности, он может быть бесконечным).

Для точек разрыва любого типа не требуется существования f(х₀).

П ример: . Любая точка, кроме х₀=0, принадлежит области определения, поэтому функция в ней непрерывна. При х-0 1/x-, поэтому 2^1/х0, т.е. конечный предел слева существует. При х+0 1/x+, поэтому 2^1/х, т.е. конечного предела справа не существует, следовательно, точка х₀=0 - точка разрыва второго рода. Второй пример - функция , рассмотренный в разделе 4.4.1.1. Определение предела функции (график - слева; х 0). Эта функция не имеет ни левого, ни правого односторонних пределов при х0, т.е. х₀=0 - точка разрыва второго рода.

5.4.3. Примеры разрывных функций. Исследование функций на непрерывность.

Классическими примерами разрывных функций служат функции Дирихле и Римана, определённые в разделе 4.1. Определение функции. Терминология. Функция Дирихле очевидно имеет разрывы второго рода в каждой точке, так как ни в одной точке не существует ни левого, ни правого пределов (раздел 4.4.1.1. Определение предела функции в точке). Относительно функции Римана

т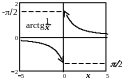 ам же было доказано, что эта функция не имеет предела при х  х₀, если х₀ рационально (следовательно, каждая рациональная точка - точка разрыва второго рода), и имеет предел, равный нулю, если х₀ иррационально (следовательно, каждая иррациональная точка - точка непрерывности).

Решение задач на исследование элементарных функций на непрерывность обычно не вызывает проблем, если хорошо осмыслены определения предела и непрерывности и наработана техника нахождения пределов. Примеры: Исследовать функции на непрерывность:

1 . . , поэтому функция непрерывна во всех точках х0. Найдём . При х-0 1х -, arctg(1/x) -/2; при х+0 1х+, arctg(1/x) /2, т.е. не существует, но существуют односторонние пределы, следовательно, точка х=0 - точка разрыва первого рода.

2. . Исследовать на непрерывность надо точку х₁=1

и точки, в которых . Решая уравнение 1/(x-1)=2, находим х₂=3/2. Пусть х1-0, тогда х-1 -0, 1/(x-1)  -, 0, у1/4. Пусть х1+0, тогда х-1 +0, 1/(x-1)  +, +, у0. Пусть, далее, х3/2-0, тогда х-11/2-0, 1/(x-1) 2+0 (вследствие убывания функции 1/(x-1)), 4+0, 4-  -0,

у -. Если х3/2+0, тогда х-11/2+0, 1/(x-1) 2-0, 4-0, 4-  +0, у +. Если ещё убедиться, что при х и учесть монотонность функции на каждом из промежутков (-,1), (1, 3/2), (3/2,+), то полученной информации вполне достаточно для построения графика этой не самой простой функции. Результат: точка х₁=1 - точка разрыва первого рода, точка х₂=3/2 - точка разрыва второго рода.

3 . . . Эта функция является элементарной функцией, поэтому она непрерывна во всех точках своей области определения. Исследуем точки х=6. При х+6 знаменатель стремится к нулю, числитель строго положителен, поэтому конечного предела быть не может, следовательно, это точка разрыва второго рода. При х -6 получается неопределённость , раскрываем её: при х -6. Таким образом, точка х= -6 - точка устранимого разрыва.