10. Гиперболические функции. Определение гиперболических функций.

Гиперболическими называются функции

- синус гиперболический; - косинус гиперболический;

- тангенс гиперболический;

- котангенс гиперболический.

Графики гиперболических функций:

С оотношения между гиперболическими функциями.

Исходя из определения гиперболических функций можно получить различные соотношения между этими функциями, схожие с соответствующими соотношениями между тригонометрическими функциями, или, в некоторых случаях, отличающиеся знаком перед некоторыми слагаемыми. Так, прямой подстановкой проверяется равенство (основное гиперболическое тождество, играющее в теории гиперболических функций ту же роль, какую в тригонометрии играет основное тригонометрическое тождество ).

Прямой проверкой или из основного гиперболического тождества можно получить аналог любой тригонометрической формулы, например

sh 2x = 2 shx chx

и т.д. Получать эти соотношения можно также руководствуясь мнемоническим правилом (оно доказывается в комплексном анализе): вместо cos x пишется ch x, а вместо sin x пишется ish x, где i - мнимая единица ( i= i = -1).

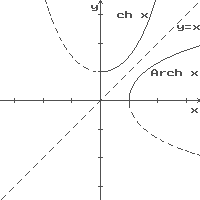
Обратные гиперболические функции.

Обратные гиперболические функции определяются как функции, обратные соответствующим гиперболическим функциям. например:

если y = Ar sh x, то x = sh y, где : x  R , y  R.

Л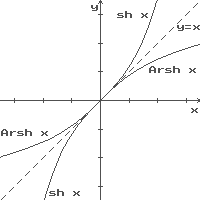 юбую обратную гиперболическую функцию можно выразить через логарифм натуральный. Так, решая уравнение относительно y с помощью подстановки z = e ^x, получим для z квадратное уравнение , при решении которого надо взять положительный корень , и окончательно . Для остальных функций так же можно получить

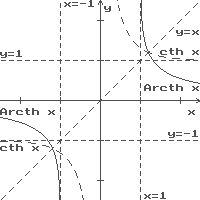
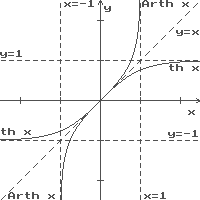
Справа и ниже на рисунках приведены графики прямых и обратных гиперболических функций.

9. Примеры неэлементарных функций

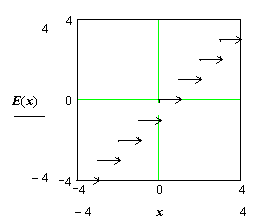Функция Е(х) - целая часть х - наибольшее целое число, не превосходящее х (график справа);

Функция Дирихле:

Функция Римана:

Г рафик функции Римана на отрезке [1,2] качественно изображён справа (построены рациональные точки со знаменателями ). Основной факт, который очевиден из рисунка и который нам понадобится в дальнейшем – при любом 0 выше линии у= лежит не более чем конечное число точек графика.