4. Границы числовых множеств.

Пусть Х={x|xR} - некоторое подмножество множества действительных чисел.

Определения.

Если существует число МR такое, что для хХ выполняется неравенство х<М, то множество Х называется ограниченным сверху (числом М). Число М называется верхней границей множества Х.

Если существует число mR такое, что для хХ выполняется неравенство х>m, то множество Х называется ограниченным снизу (числом m). Число m называется нижней границей множества Х.

Если существует число МR такое, что для хХ выполняется неравенство |х|<М, то множество Х называется ограниченным.

Теорема. Множество ограничено тогда и только тогда, когда оно ограничено сверху и снизу.

Если множество Х ограничено сверху, то множество его верхних границ бесконечно (если число М - верхняя граница, то верхними границами будут числа М+1, М+2 и т.д.). Обозначим У множество верхних границ множества Х. Множество У ограничено снизу (любым элементом множества Х).

Возможны два случая: либо множество Х имеет максимальный элемент (например, если

Х – отрезок [0, 1], то максимальный элемент равен 1), в этом случае множество верхних границ не имеет минимального элемента; либо множество Х не имеет максимального элемента (например, если Х = (0, 1)), в этом случае множество верхних границ имеет минимальный элемент.

Определение. Точной верхней границей, или верхней гранью, множества Х, ограниченного сверху, называется максимальный элемент этого множества, если он существует, и минимальный элемент множества верхних границ, если множество Х не имеет максимального элемента.

Для обозначения применяются: символы sup X или sup{x}.

Свойства верхней грани:

Пусть М^*= sup X - верхняя грань множества Х. Тогда

Д ля хХ выполняется неравенство х М^*.

Любое число, меньшее М^*, не будет верхней границей множества Х, т.е. для >0 xX такой, что х> М^*-.

Аналогичным образом, если множество Х ограничено снизу, то множество его нижних границ бесконечно. Обозначим Z множество нижних границ множества Х. Множество Z ограничено сверху (любым элементом множества Х).

Определение. Точной нижней границей, или нижней гранью, множества Х, ограниченного снизу, называется минимальный элемент этого множества, если он существует, и максимальный элемент множества нижних границ, если множество Х не имеет минимального элемента.

Для обозначения применяются: символы inf X или inf{x}.

Свойства нижней грани:

Пусть М_*= inf X - нижняя грань множества Х. Тогда

Для хХ выполняется неравенство х  М_*.

Любое число, большее М_*, не будет нижней границей множества Х, т.е. для >0 xX такой, что х М_*+.

5. Функция. Монотонность. Ограниченность.

х – называется независимой переменной.

у – зависимой.

Функцию можно задавать равенством (у=х²)

Таблицей

Х	Х1	Х2	Х3	Х4
У	У1	У2	У3	У4

Графиком, то есть множеством точек с координатами (x,f(x)) на плоскости:

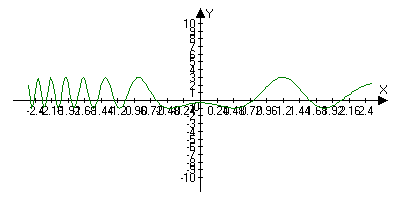
Определение f(x) монотонности: Пусть Х принадлежит области определение D ( ]xD)

Пусть Х подмножество в области определения в f(x).

Функция у=f(x) называется:

1. Возрастающая на Х, если для любого х₁;х₂ принадлежащие Х: х₁<x₂f(x₁)<f(x₂)

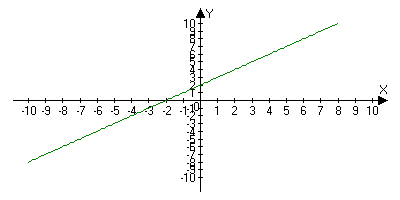
2. Убывающий на Х, если для любого х₁;х₂ принадлежащие Х: х₁<x₂f(x₁)>f(x₂)

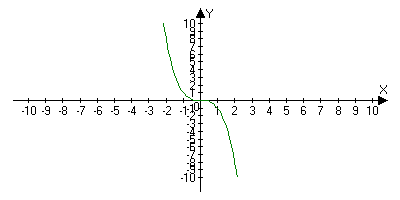
3) Не убывающий на Х, если для любого х₁;х₂ принадлежащие Х: х₁<x₂f(x₁)f(x₂)

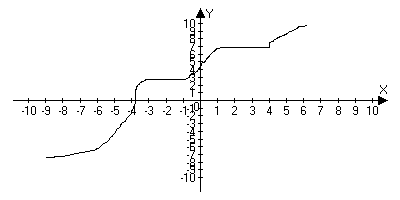
4. Не возрастающая на Х, если для любого х₁;х₂ принадлежащие Х: х₁<x₂f(x₁)f(x₂)

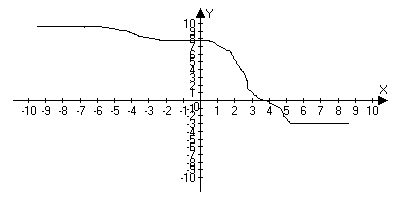
Определение:

Ограниченность. Пусть Х включает D y=f(x) называется:

1. Ограниченной сверху на Х если существует В, так что для любого х принадлежащего Х выполняется f(x)B

2. Ограниченной снизу на Х если существует А, так что для любого х принадлежащего Х выполняется А f(x)

3. Ограниченной и сверху и снизу на Х если существует А,В, так что для любого х принадлежащего Х выполняется А f(x)В, или существует С, так что для любого х принадлежащего Х выполняется f(x)С