1895

Министерство транспорта Российской Федерации

Федеральное агентство железнодорожного транспорта

Государственное образовательное учреждение высшего профессионального образования

Самарская государственная академия путей сообщения

Кафедра «Высшая математика»

В.А. Паняев

Н.М. Латыпова

Комплексные числа

Методические указания и индивидуальные задания по разделу «Комплексные числа» для студентов всех специальностей

очной формы обучения

Самара 2007

УДК 517

Высшая математика : методические указания и индивидуальные задания по разделу «Комплексные числа» для студентов всех специальностей очной формы обучения / составители : В.А. Паняев, Н.М. Латыпова. – Самара : СамГАПС, 2007. – 24 с.

Утверждено на заседание кафедры 03.10.2006, протокол №2.

Печатается по решению редакционно-издательского совета академии.

Методические указания и индивидуальные задания составлены в соответствии с Государственным образовательным стандартом и действующей программой по высшей математике для технических вузов.

Составители: к.т.н., доцент В.А. Паняев

к.ф.-м.н., доцент Н.М. Латыпова

Рецензенты: к.т.н., доцент СГАУ В.В. Максимов

к.ф.-м.н., доцент СамГАПС В.Л. Шур

Под редакцией составителей

Подписано в печать 19.04.2007. Формат 60 84 1/16.

Бумага офсетная. Печать офсетная. Усл. п. л. 1,5.

Тираж 150 экз. Заказ № 68.

© Самарская государственная академия путей сообщения, 2007 Комплексные числа

1. Числовые множества и комплексные числа

История введения в математику понятия комплексного числа отражает общую тенденцию развития математических исчислений, когда использование новых математических операций приводило к необходимости расширения числовой области.

Понятие числа, являясь первичным и основным в математике, прошло, как известно, длительный путь исторического развития.

Множество натуральных чисел появилось в связи с необходимостью проводить счет (сложение и умножение) реальных предметов. Потребности практики и развитие математики привели к необходимости введения обратных операций – вычитания, деления и извлечения корня. Натуральный ряд был дополнен противоположными натуральным по значению отрицательными числами и нулем, что привело к возникновению множества целых чисел , затем рациональных , , и иррациональных . Последние были введены в связи с необходимостью измерения отрезков, длина которых не является рациональным числом.

Операция извлечения корня явилась причиной введения общего понятия действительного числа. Как известно, множества рациональных и иррациональных чисел в совокупности образуют упорядоченное множество действительных чисел , где , т.е. , и изображают точками непрерывной числовой оси . С их помощью можно выразить длину любого реального отрезка.

Для рассмотренных числовых множеств имеет место такое последовательное включение:

Понятие комплексного числа z представляет расширение понятия действительных чисел, которые можно рассматривать как некоторое подмножество в множестве комплексных чисел , т.е.

Исторически комплексные числа z обязаны своим возникновением попыткам найти решение алгебраических уравнений. Частные случай, связанный с необходимостью извлечения квадратного корня или корня четной степени из отрицательного числа привел к необходимости введения мнимых чисел, в отличие от действительных, и появлению множества комплексных чисел .

В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. Рассмотрим решение простейшего кубического уравнения :

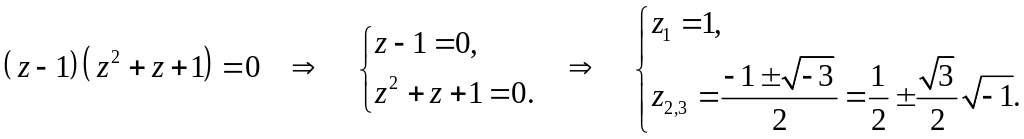(1.1)

Чтобы объяснить парадокс – извлечение квадратного корня из отрицательного числа, итальянский ученый-алгебраист эпохи Возрождения Джироламо Кардано в 1545 г. предложил ввести в математические операции числа новой природы, назвав их «чисто отрицательными», однако считая их бесполезными для приложений. В 1572 г. итальянский алгебраист Раффаэле Бомбелли установил первые арифметические операции над такими числами.

Название «мнимые числа» ввел в 1637 г. французский математик и философ Рэне Декарт. В 1777 г. один из крупнейших математиков XVIII века Леонард Эйлер для обозначения предложил использовать первую букву французского слова (мнимый, воображаемый, несуществующий), т.е. ввести обозначение в структуру комплексных чисел. Тогда корни z_2,3 выше приведенного кубического уравнения записываются в виде

(1.2)

т.е. в алгебраической форме комплексное число принимает вид , где a и b – действительные числа, мнимая единица.

Общая теория корней n-й степени из отрицательных и любых комплексных чисел основана на формуле английского математика французского происхождения Абрахама де Муавра, и была построена на рубеже XVII – XVIII веков.

В конце XVIII – начале XIX века было получено геометрическое истолкование комплексных чисел. Независимо друг от друга датчанин Каспар Вессель, француз Жан Аргон и крупнейший немецкий математик Карл Гаусс предложил изображать комплексное число точкой М(а,b) на координатной комплексной плоскости. Позднее пришли к выводу, что такое число удобнее изображать не самой точкой, а радиусом-вектором , проведенным в точку М из начала координат, что позволило рассматривать операции сложения и вычитания комплексных чисел как операции над соответствующими векторами.

Геометрический подход к изображению комплексных чисел и накопленные знания об их свойствах создали предпосылки для разработки теории функций комплексной переменной. Комплексные числа в настоящее время находят широкое применение в различных областях науки и техники: при расчетах электрических цепей, решении обыкновенных дифференциальных уравнений и дифференциальных уравнений математической физики, при изучении течения жидкостей и газа (аэро и гидродинамика), решении задач теории упругости, проблем квантовой теории поля и многих других задач.