8. Линейные комбинации

Рассмотрим два n – мерных вектора а = (а₁, а₂, . . . , а_n)^Т и b = (b₁, b₂, . . . , b_n)^T. Вектор а называется пропорциональным вектору b , если существует число k, такое что a = kb, т. е. если компоненты вектора а пропорциональны компонентам вектора b.

Согласно определению, нуль-вектор пропорционален любому вектору, так как справедливо равенство 0_n = 0_n∙a.

Понятие пропорциональности двух векторов является частным случаем более общего понятия – линейной комбинации.

Имея набор, состоящий из n векторов (а₁, а₂, . . . , а_n)^Т, и набор из n чисел (k₁, k₂, . . . , k_n) можно составить линейную комбинацию векторов (а_i) с коэффициентами (k_i). Для этого надо i-й вектор умножить на i-й скаляр и все полученные таким образом произведения сложить, т. е. линейной комбинации векторов (а_i) с коэффициентами (k_i) называется вектор b, определенный равенством

b = k₁a₁+k₂a₂+ . . . +k_na_n.

Эта процедура есть не что иное, как умножение матрицы А со столбцами (а_i) на вектор с компонентами (k_i), т. е. b = (а₁, а₂, . . . , а_n) (k₁, k₂, . . . , k_n)^T.

Таким образом, любое произведение матрицы и вектора есть линейная комбинация столбцов матрицы с коэффициентами, равными компонентам вектора.

Линейную комбинацию с нулевыми коэффициентами принято называть тривиальной, а если хотя бы один из коэффициентов в линейной комбинации отличен от нуля, ее называют нетривиальной.

Например, вектор b = (12; 46) является линейной комбинацией векторов

а₁ = (12; 12) и а₂ = (0; 34): b = а₁+а₂.

Частным случаем линейной комбинации является неотрицательная комбинация (k_i 0), в которой выполняется условие k₁+k₂+ . . . +k_n = 1 . Тогда линейная комбинация называется выпуклой комбинацией.

1.1.9. Основные свойства определителя

Свойство 1. Равноправие строк и столбцов. При транспонировании матрицы ее определитель не меняется.

Свойство 2. Если все элементы какого-либо столбца определителя равны нулю, то и сам определитель равен нулю.

Свойство 3. При перестановке двух любых столбцов определителя его знак меняется на противоположный, а абсолютная величина остается неизменной.

Следствие 1. Определитель с двумя одинаковыми столбцами равен 0.

Свойство 4. Линейность. Если j-й столбец А_j определителя D является линейной комбинацией

А_j = kB+mC

двух произвольных столбцов В и С, то и сам определитель оказывается линейной комбинацией

D = D_j(kB+mC) = kD_j(B)+mD_j(C)

определителей D_j(B) и D_j(C).

Следствие 2. При умножении любого столбца определителя на произвольное число k сам определитель умножается на то же число.

Следствие 3. Если какой-либо столбец определителя является линейной комбинацией других его столбцов, то определитель D равен нулю.

Свойство 5. Определитель не изменится, если к любому его столбцу прибавить произвольную линейную комбинацию остальных его столбцов.

Свойство 6. Сумма произведений всех элементов некоторого столбца определителя на алгебраические дополнения соответствующих элементов другого столбца равно 0.

a_1kA_1j+a_2kA_2j+ . . . +a_nkA_nj = 0.

Пример 1.10. Вычислить определитель

.

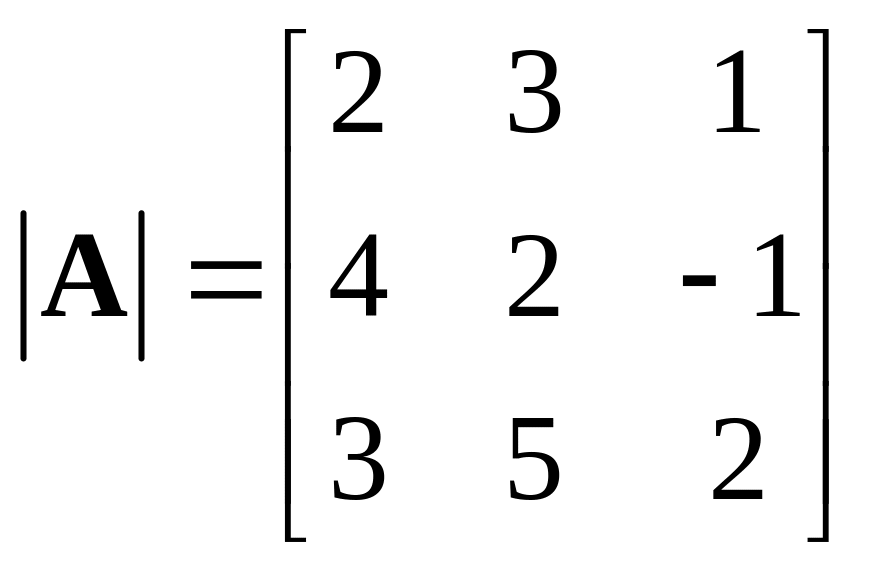На основании теоремы определитель равен сумме произведений всех элементов любого столбца на их алгебраические дополнения. Разложим определитель |A| по элементам второго столбца

|A| = 3A₁₂+2A₂₂+5A₃₂

.

Пример 1.11. Вычислить определитель четвертого порядка

.

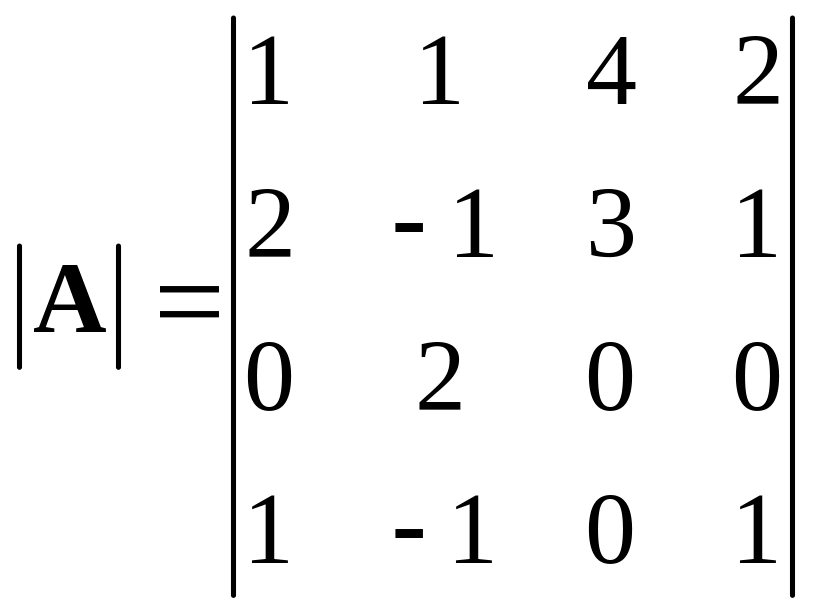Согласно теореме определитель равен сумме произведений всех элементов любой строки на их алгебраические дополнения. Разложим определитель по элементам третьей строки

|A| = 0·A₃₁+2·A₃₂+0·A₃₃+0·A₃₄ , |A| = 2·A₃₂ .

Алгебраическое дополнение А₃₂ равно минору М₃₂ , умноженному на (-1)³⁺²= -1. Поэтому,

.

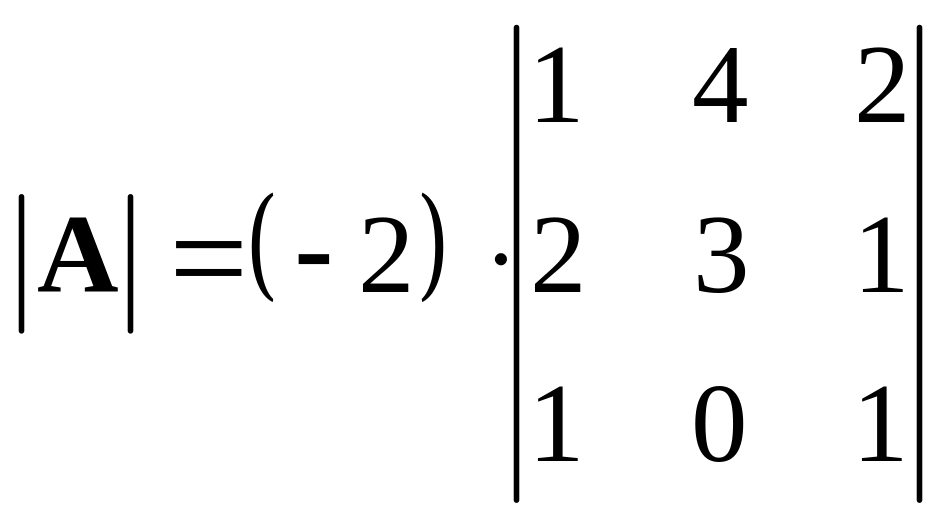Согласно свойству 5 к любому столбцу определителя можно прибавить произвольную линейную комбинацию других его столбцов. Прибавим к третьему столбцу первый, умноженный на –1, т.е. фактически вычтем из третьего столбца первый. Получим

.

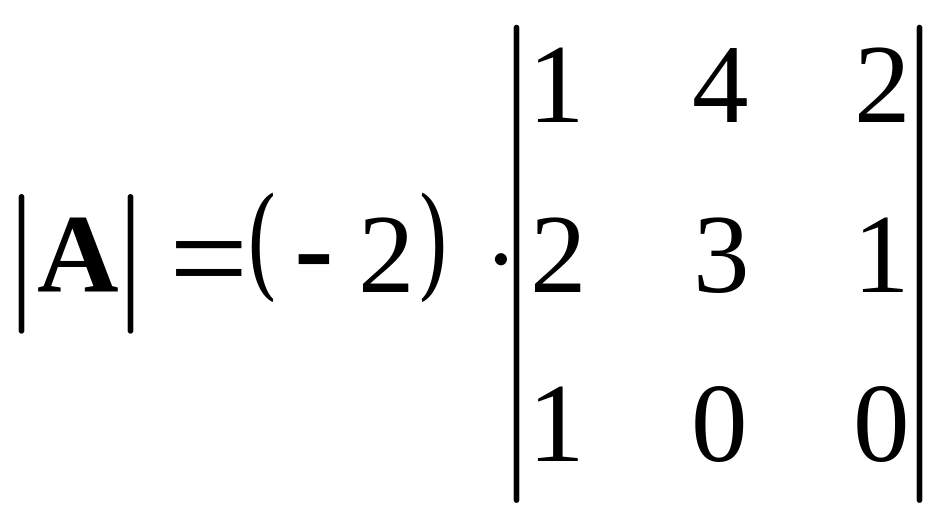Вновь разложим определитель по элементам последней строки. Поскольку все элементы, кроме первого, в ней равны нулю, то из трех слагаемых не равным нулю окажется только одно. Значит

.