
- •1. Введение в вычислительную линейную алгебру
- •1.1. Предварительные сведения
- •Скаляры и векторы
- •Матрицы
- •Специальные матрицы
- •Норма матрицы
- •Операции над векторами и матрицами
- •1.1.6. Определитель (детерминант) матрицы
- •Для матрицы
- •Главный минор и ранг матрицы
- •Линейные комбинации
- •1.1.9. Основные свойства определителя
- •1.1.10. Основные свойства ранга матрицы
- •1.1.11. Обратная матрица
- •1.1.12. Линейная зависимость и независимость
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«ЧФ Пермского государственного технического университета»
Бочкарев С.В.
ТЕОРИЯ ОПТИМИЗАЦИИ
Учебное пособие
Пермь 2008
Введение
Оптимизация − это выбор наилучшего решения. О некоторых задачах определения максимальных и минимальных значений писали еще Аристотель (384-322 годы до н. э.), Евклид (III в до н. э.) и Архимед (287- 212 годы до н.э.). По легенде основание города Карфагена (825 г. до н. э.) связывают с древнейшей задачей определения замкнутой плоской кривой, охватывающей фигуру максимально возможной площади. Подобные задачи называются изопериметрическими.
Начиная с XVII века, доминирующим становится представление о том, что законы окружающего нас мира являются следствием некоторых вариационных принципов. Первым из них был принцип П. Ферма (1660 г.), в соответствии с которым траектория света, распространяющегося от одной точки к другой, должна быть такова, чтобы время прохождения света вдоль этой траектории было минимально возможным. Впоследствии были предложены различные вариационные принципы, например: принцип стационарного действия У. Р. Гамильтона (1834 г.), принцип виртуальных перемещений, принцип наименьшего принуждения и др.
Параллельно развивались и методы решения экстремальных задач. Около 1630 г. Ферма сформулировал метод исследования на экстремум для полиномов, состоящий в том, что в точке экстремума производная равняется нулю. Для общего случая этот метод получен И. Ньютоном (1671 г.) и Г. В. Лейбницем (1684 г.), работы которых знаменуют зарождение математического анализа. В 1696 г. И. Бернулли (ученик Лейбница) сформулировал задачу о кривой, соединяющей две точки A и B, двигаясь по которой из т. A в B под действием силы тяжести, т. А достигает В за минимально возможное время (задача о брахистохроне − линии быстрейшего ската).
Термин «оптимум» впервые был введен создателем дифференциального исчисления Г. Лейбницем в XVIII в. Он взял за основу латинское слово optimus , что означает «наилучший».
Однако более раннее значение этого слова, как указывает Д. Уайлд, следует связывать с именем богини древнеиталийского племени сабинов – Опы, которая считалась богиней плодородия и урожая. Согласно древнеримской мифологии, богиня Опа была женой бога времени Сатурна и матерью Юпитера, бога – охранителя римского государства. Богиня Опа держит в одной руке рог изобилия, мифологический источник благ, а в другой – весы, символизирующие измерение и решение. Имя этой богини слышится не только в латинском слове «изобилие» (в оригинале cornucopia – рог изобилия; лат. copia – множество, запас), но и в словах, употребляемых в современном языке для обозначения продуктов труда – «опус» и «опера», а также в слове «операция», означающем процесс создания продуктов труда. Дисциплина, близкая по назначению к оптимальному проектированию, имеет название «исследование операций», и в этом названии также отражено имя богини изобилия.
Дальнейшее развитие теории экстремальных задач привело в XX веке к созданию линейного программирования, выпуклого анализа и других разделов, одним из которых является теория оптимального управления.
В настоящее время теория оптимизации вносит заметный вклад в ускорение научно – технического прогресса. Это объясняется тем, что весьма актуальными стали вопросы наилучшего управления различными процессами физики, техники, экономики и др. Сюда относится задача организации производства с целью получения максимальной прибыли при заданных затратах ресурсов; задача о космическом перелете из одной точки пространства в другую с наименьшей затратой энергии, задача о быстрейшем нагреве печи до заданного температурного режима, оценка оптимальности асинхронных двигателей, оптимизация электроприводов, оптимизация объединенных электрических цепей и др. задачи.
Процесс оптимизации лежит в основе всей инженерной деятельности, поэтому классические функции инженера заключаются в том, чтобы, с одной стороны, проектировать новые, более эффективные и менее дорогостоящие технические системы и, с другой стороны, разрабатывать методы повышения качества функционирования существующих систем.
Эффективность оптимизационных методов, позволяющих осуществить выбор наилучшего варианта без непосредственной проверки всех возможных вариантов, тесно связана с широким использованием достижений в области математики путем реализации итеративных вычислительных схем с использованием ЭВМ. Поэтому для изучения основ оптимизации требуется знание теории матриц, элементов линейной алгебры и дифференциального исчисления, математического анализа.
Теория оптимизации находит эффективное применение во всех направлениях инженерной деятельности, и, в первую очередь, в следующих четырех ее областях:
1) проектирование систем и их составных частей;
2) планирование и анализ функционирования существующих систем;
3) инженерный анализ и обработка информации;
4) управление динамическими системами.
Следует иметь в виду, что оптимизация – всего лишь один этап в процессе формирования оптимального проекта или условий эффективного функционирования системы. Указанный процесс является циклическим и включает синтез (определение) структуры системы, построение модели, оптимизацию параметров модели и анализ полученного решения (рис.1.). При этом оптимальный проект или новый план функционирования системы строится на основе решения серии оптимизационных задач, способствующего дальнейшему совершенствованию системы.
Несмотря на то, что методы теории оптимизации отличаются универсальностью, их успешное применение в значительной степени зависит от профессиональной подготовки инженера, который должен иметь четкое представление о специфических особенностях изучаемой системы.

Рис. 1. Этапы процесса инженерного проектирования
1. Введение в вычислительную линейную алгебру
1.1. Предварительные сведения
Скаляры и векторы
Одиночные количественные характеристики и результаты измерений обычно формализуются понятием «скаляр» или «вещественное число». Иными словами, скалярная величина характеризуется только числом.
Формально вектор может быть определен как упорядоченный набор скаляров. Подобно тому, как вещественное число служит мерой отдельного свойства какого-либо объекта (скажем, диаметр электродвигателя), векторы используются для описания упорядоченных совокупностей свойств. Например, высота электрощита рассматривается как его первая характеристика, длина – как вторая, а ширина – как третья. Тогда электрощит, имеющий 500 мм высоты, 300 мм длины и 250 мм ширины может быть описан вектором.
Электрощит
=
![]()
Векторные величины характеризуются не только числом, но и направлением. Направление, как правило, указывается стрелкой. На рис.1.1. изображен вектор АВ. Под численным значением или длиной вектора АВ понимается длина отрезка АВ, соединяющего начало А и конец В вектора АВ.
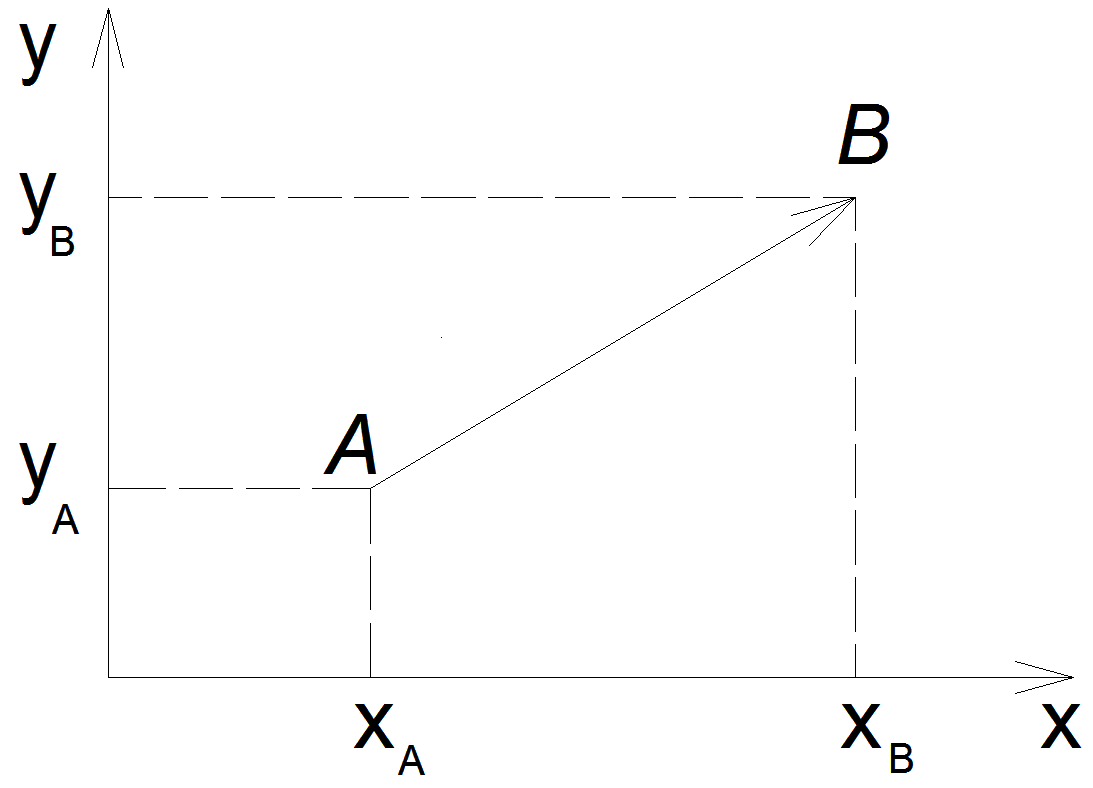
Рис.1.1. Двумерный вектор
Д лину
вектора часто называют модулем
вектора и обозначают
той же буквой, заключенной в вертикальные
черты |x|,
| АВ
| или так:
лину
вектора часто называют модулем
вектора и обозначают
той же буквой, заключенной в вертикальные
черты |x|,
| АВ
| или так:
![]() и
и
![]() .
Вектор, определенный парой чисел,
называется двумерным вектором.
Геометрически двумерному вектору
соответствует точка на плоскости.
Аналогично вектор, определенный
упорядоченной тройкой чисел (xA,
yA,
zA),
называется трехмерным вектором.
Геометрически трехмерному вектору
соответствует точка пространства
(рис.1.2).
.
Вектор, определенный парой чисел,
называется двумерным вектором.
Геометрически двумерному вектору
соответствует точка на плоскости.
Аналогично вектор, определенный
упорядоченной тройкой чисел (xA,
yA,
zA),
называется трехмерным вектором.
Геометрически трехмерному вектору
соответствует точка пространства
(рис.1.2).
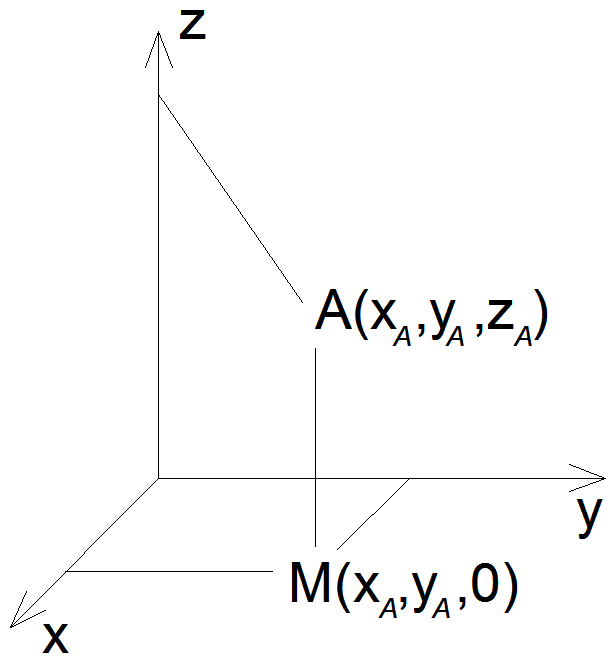
Рис.1.2. Трёхмерный вектор
Стандартная форма записи вектора опирается на привычный порядок чтения текстов сверху – вниз. Соответственно векторы изображаются вертикальными столбцами чисел с первой компонентой в верхней позиции. Вектор является вектором – столбцом в общем виде
=
![]()
или n-мерным вектором. Числа x1, x2, . . . , xn называют компонентами или координатами вектора . Последние, как правило, нумеруются индексом, пробегающим значения от 1 до n, где n – размерность вектора. Обозначением отдельной компоненты вектора будет служить его имя с нижним индексом, указывающим номер этой компоненты. Так, через x2, принято обозначать вторую компоненту вектора .
Если из вектора – столбца хотят получить вектор – строку, то эта операция называется транспонированием. В этом случае вектор – строка записывается в виде = (x1, x2, . . . , xn)T . Таким образом, если – вектор – столбец, тогда Т – вектор – строка, при этом ( Т)Т – вновь вектор – столбец, причем =( T)T .
Вектор, все компоненты которого равны нулю, называется нуль - вектором и обозначается 0 = (0, 0, . . . , 0) или 0n . В дальнейшем при обозначении векторов черту будем опускать.
Два вектора считаются одинаковыми, если их соответственные компоненты равны. Это определение предполагает, что проверяемые на совпадение вектора имеют одинаковую размерность, т.е. xi = yi, i =1, 2, . . . , n.
Суммой векторов x и y называют вектор, обозначаемый x+y, компоненты которого находят по формуле:
x+y = (x1+y1, x2+y2, . . ., xn+yn). (1.1)
Разность векторов x и y определяют следующим образом:
х–y = (x1-y1, x2-y2, . . . , xn-yn). (1.2)
Произведением вектора x на вещественное число а называется вектор, обозначаемый аx, компоненты которого находят по формуле:
аx = (аx1, аx2, . . . , аxn). (1.3)
Из приведенных определений непосредственно вытекает справедливость следующих равенств:
Коммутативность: x+y = y+x.
Ассоциативность: (x+y)+z = x+(y+z);
x+0n = x;
0x=0n;
a(x+y) = ax+ay;
(a1+a2)x = a1x+a2x.
Введем понятие скалярного произведения двух векторов. Если y – вектор строка размерности n, а x – вектор – столбец размерности n, то скалярное произведение двух векторов определяется равенством
![]() или
или
![]() (1.4)
(1.4)
Например,
y =
(1, -2, 0)T
, х =
![]() ,<y,х>
= 1∙2+(-2) 3+0∙1 = –4
,<y,х>
= 1∙2+(-2) 3+0∙1 = –4
Итак, чтобы получить скалярное произведение двух векторов надо перемножить соответствующие компоненты и результат сложить. Результат скалярного произведения – число.
Пример 1.1. Найти компоненты вектора: x= –2.5a+1.5b+c , если а = (2, 3, 4, 5)Т, b = (1, 0, 2, 1)T, c = (0, 4, 5, 1)T.
Ответ: (-3.5, 11.5, -12, -12)Т.
Пример 1.2. Сложить вектора: а) 3(1, -7, 5)T-2(0, 2, -2)Т+(-2, 26, -18)Т =(1, 1, 1)Т; б) (2, 1, -1, 3)T+(1, -1, -2, 1)T-(-4, 1, 5, -1)T=(8, -2, -10, 2).
Среди
скалярных произведений отметим xTx
= <x,
x
> =
![]() .
.
Отметим свойства, которыми обладает скалярное произведение
<х, у> = <у, х>;
<х+у, z> = <x, z>+<y, z>;
<ax, y> = a<x, y>;
<x, x> > = 0 (равенство имеет место тогда и только тогда, когда х нулевой вектор 0n).
Совокупность всех n-мерных векторов, для которых введены операции сложения, вычитания, умножения на вещественное число, а также скалярное произведение согласно формулам (1.1)…(1.4), называют n – мерным вещественным евклидовым пространством и обозначают En. Для краткости это пространство будем называть просто евклидовым пространством.
Множество вещественных чисел далее будем обозначать E. Введем понятие – расширенная числовая прямая Ē=EU {-∞; +∞} (U – объединение). Множество E является примером одномерного евклидова пространства. Пространство E2 будем геометрически интерпретировать как совокупность точек плоскости с фиксированной прямоугольной системой координат или же, как совокупность векторов на этой плоскости, начало которых совпадает с началом прямоугольной системы координат. Пространство E3 имеет аналогичную интерпретацию в пространстве трех измерений. Элементы пространства En будем называть также точками.
Положительное
значение квадратного корня хТх
есть норма ||x||
или длина вектора х
![]() En(х
принадлежит множеству Еn),
определяемая по формуле:
En(х
принадлежит множеству Еn),
определяемая по формуле:
||x||
=
 (1.5)
(1.5)
Сформулируем основные свойства нормы вектора:
![]() )
||x||
≥ 0, причем ||x||
= 0 тогда и только тогда, когда х =
0n;
)
||x||
≥ 0, причем ||x||
= 0 тогда и только тогда, когда х =
0n;
![]() )
||ax||
= |a|
||x||,
где а
– число;
)
||ax||
= |a|
||x||,
где а
– число;
![]() )
||x+y||
< = ||x||
+||y||
– неравенство треугольника;
)
||x+y||
< = ||x||
+||y||
– неравенство треугольника;
![]() )
|<xy>|
< = ||x||·||y||
– неравенство Коши – Буняковского.
)
|<xy>|
< = ||x||·||y||
– неравенство Коши – Буняковского.
Если норма определяется равенством (1.5), то всякое евклидово пространство становится нормированным. Полное евклидово пространство называется гильбертовым.
Расстояние между точками х и у евклидова пространства, обозначают через (x, y) и определяют следующим образом:
(х,
у) = ||x-y||
=
 .
.
