
- •Билет №1 (Управляемые объекты. Фазовые траектории. Процесс управления)
- •Билет №2 (Задача управления. Уравнение движения объекта)
- •Общая постановка задачи оптимального управления.
- •Билет №4 (Сопряженная система. Гамильтониан)
- •Билет №5 (Принцип максимума для задачи оу с закрепленными концами)
- •Задача синтеза
- •Билет №8 (Линейный оптимальные быстродействия. Теорема для линейных оптимальных быстродействиях)
Билет №5 (Принцип максимума для задачи оу с закрепленными концами)
Следующая теорема (необходимое условие оптимальности), главным содержанием которой является равенство (22), имеет вид:
Пусть u(t), t0≤t≤t1, такое допустимое управление, что соответствующая ему фазовая траектория (t), исходящая в момент времени t0 из точки (0,x0), проходит в момент времени t1 через некоторую точку прямой П (см. рис. 6). Для оптимальности управления u(t) и траектории (t) необходимо существование такой ненулевой непрерывной вектор-функции (t) = {ψ0(t),ψ1(t),…ψn(t)}, соответствующей (t) и u(t), что:
1) при любом t, t0≤t≤t1, функция
H(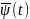 ,x(t),u)
переменного
u
достигает в точке
u
,x(t),u)
переменного
u
достигает в точке
u =u(t)
максимума
M(
(t),
x(t))
=u(t)
максимума
M(
(t),
x(t))
H( ,x(t),u) = M( (t), x(t)) (22)
2) в начальный момент времени t1, выполнено соотношение ψ0(t1)≤0 и
M( (t1), x(t1)) = 0.
Если максимум функции H( ,x(t),u) достигается во внутренней точке области управления , то для выполнения условия максимума (22) необходимо
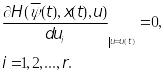 (23)
(23)
Билет №6(Принцип максимума для задачи ОУ по быстродействию)
Пример задачи синтеза
Рассмотрим
уравнение
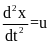 ,где u–вещественное
число, удовлетворяющее условию |u|≤1,
управляющий параметр.
,где u–вещественное
число, удовлетворяющее условию |u|≤1,
управляющий параметр.
В
фазовых координатах: x1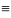 x,
x2=
x,
x2=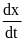 .
.
Это уравнение будет иметь следующий вид:
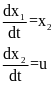 -система
двух дифференциальных уравнений первого
порядка. (1)
-система
двух дифференциальных уравнений первого
порядка. (1)
Рассмотрим (для фазовой точки, движущейся по закону (1)) задачу о быстрейшем попадании в начало координат (0,0) из любого заданного начального состояния x0, иначе говоря, мы будем рассматривать задачу об оптимальном быстродействии.
Имеем задачу с закрепленными концами.
Решение:
Функция Гамильтона имеет вид:
H=(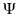 ,f),
где f1=x2,
f2=u,
,f),
где f1=x2,
f2=u,
 ,
,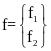 - вектор-функция, тогда:
- вектор-функция, тогда:
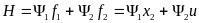 .
(2)
.
(2)
Для
сопряженных (вспомогательных) переменных
 и
и
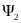 мы получаем систему сопряженных
уравнений из Гамильтоновой системы:
мы получаем систему сопряженных
уравнений из Гамильтоновой системы:
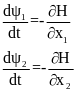
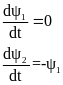
.
Это система линейных дифференциальных уравнений с постоянными коэффициентами для сопряженных переменных и .
Рассмотрим решение первого уравнения.
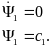
Подставляя, во второе дифференциальное уравнение получаем:
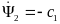 .
.
Проинтегрировав, обе части уравнения получаем:
 .
.
Соотношение
принципа максимума (9) дает нам, учитывая
(8) и условия максимума для
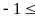 u
u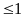 ,
u(t)=
,
u(t)=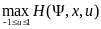 ,
из условия максимума.
,
из условия максимума.
Подставляем
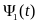 и
и
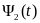 в (2) получаем:
в (2) получаем:
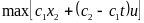 .
.
Находим максимум гамильтониана в любой момент времени, при фиксированных значениях и . Функция H становится линейной функцией u.
u=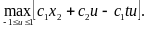
u(t)=1.
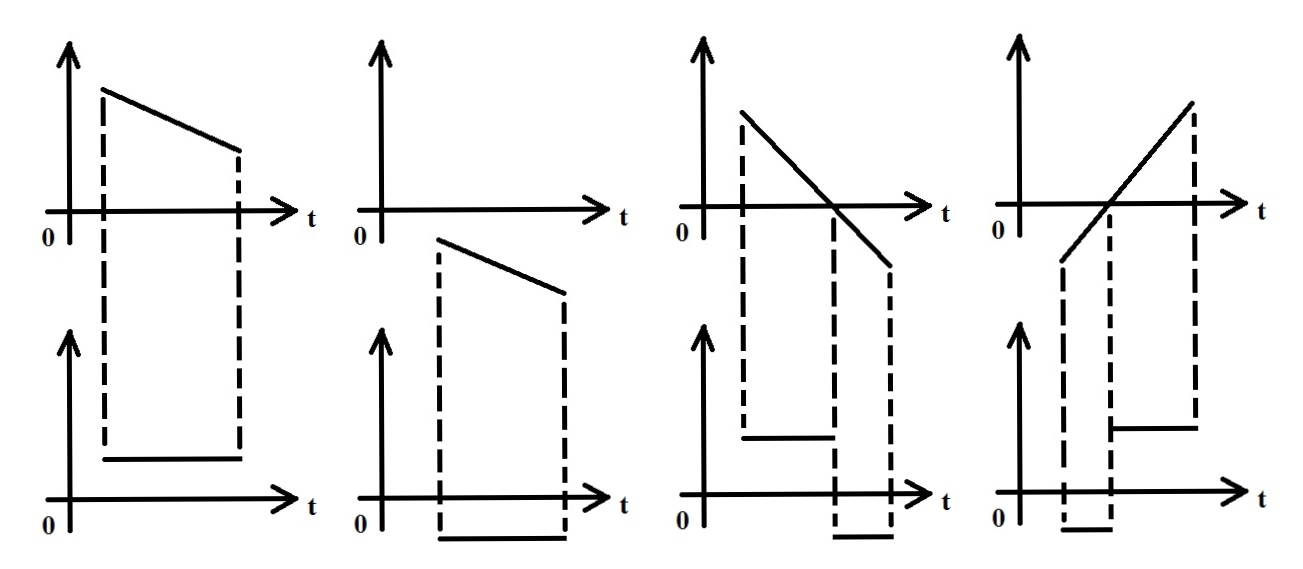
Рис.10
Для данной функции Гамильтона u принимает граничные значения
1,если
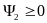
u(t)= (3)
1,если
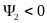 .
.
Такая функция имеет вид: u=sign .
Из
(3) следует, что каждое оптимальное
управление u(t),
t0≤t≤t1
является
кусочно-постоянной функцией принимающей
значения
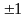 и имеющей не более двух интервалов
постоянства (потому что линейная функция
или
и имеющей не более двух интервалов
постоянства (потому что линейная функция
или
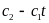 имеет не более одного раза смены знака
на интервале от t0
до t1)
(рис. 10).
имеет не более одного раза смены знака
на интервале от t0
до t1)
(рис. 10).
Далее, преступаем к решению системы дифференциальных уравнений для фазовых координат:
1)
Для отрезка времени на котором
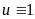 .
В этом случае имеем следующую систему
дифференциальных уравнений
.
В этом случае имеем следующую систему
дифференциальных уравнений
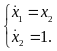
Получаем:
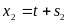
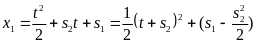 ,
где s1
и s2-
постоянные интегрирования.
,
где s1
и s2-
постоянные интегрирования.
Преобразуем и получим зависимость:
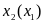
 ,
где
,
где
 .
.
Это уравнение параболы при заданном s (рис. 11).
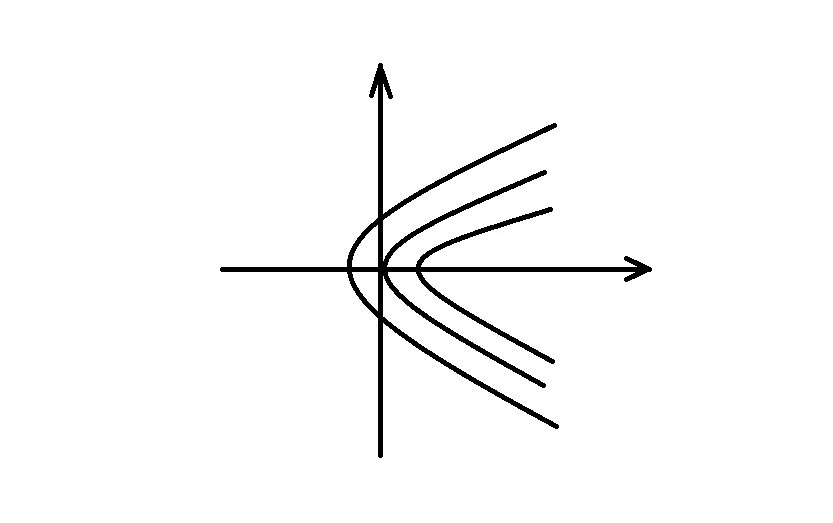
Рис.11
Определим направление движения фазовой точки по данным траекториям.
По
этим параболам (рис. 11) фазовая точка
движется снизу вверх, так как
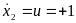 - производная больше нуля, то x2
возрастает для любого t.
- производная больше нуля, то x2
возрастает для любого t.
2)
Для отрезка времени на котором
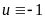 имеем:
имеем:
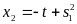
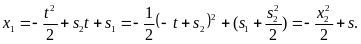
Это семейство парабол (рис. 12).
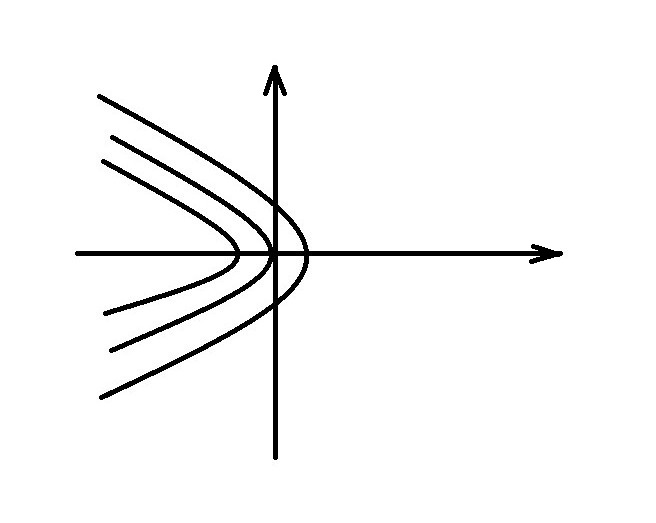
Рис.12
Движение
сверху вниз, так как
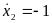 .
.
Каждое
оптимальное
управление u(t)
является кусочно-постоянной функцией,
принимающей значения
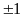 ,
и имеющий не более двух интервалов
постоянства (не более одной точки
пересечения с осью абсцисс).
,
и имеющий не более двух интервалов
постоянства (не более одной точки
пересечения с осью абсцисс).
Если управление u(t) сначала, в течение некоторого времени, равнялось +1, а затем стало равно -1, то фазовая траектория движения по двум "кускам" парабол, примыкающих друг к другу, причем второй из этих "кусков" лежит на первой параболе (рис. 13).
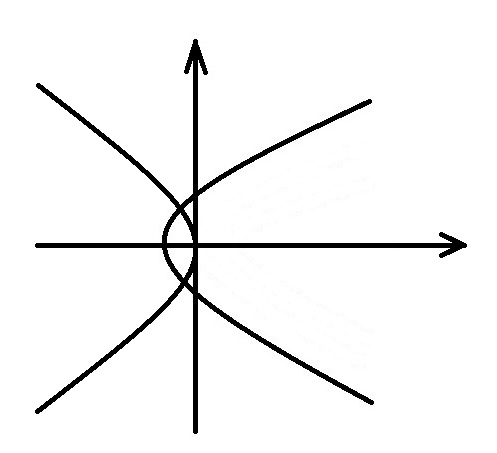
Рис.13
Наискорейший путь.
Причем второй из этих "кусков" лежит на параболе (u=-1), которая проходит через начало координат.
Если u равнялось -1, а затем +1, то траектория движения будет (рис. 14).
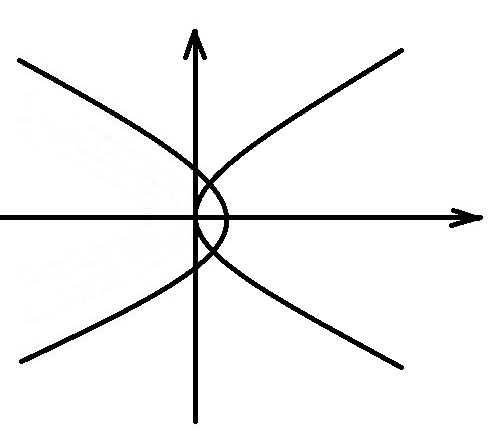
Все семейство парабол показано на следующем рисунке (рис. 15).
![]()
Рис.15
Все семейство точек выше AOB будет смотри (рис. 15).
Область I: Семейство траекторий, ведущее в начало координат, без переключения управления.
Область II: Семейство траекторий, ведущее в начало координат, с управлением u=-1.
Область III: Для всех точек, находящихся выше линии AOB траектории будут состоять из "куска" траектории с управлением u=-1, до тех пор, пока фазовая точка не попадёт на параболу AO (рис. 15).
Область IV: Для всех точек, находящихся ниже линии AOB траектории будут состоять из "куска" траектории с управлением u=1, до тех пор, пока фазовая точка не попадет на параболу BO.
Полученное в рассмотренном примере, решение оптимальной задачи можно истолковать следующим образом.
Обозначим v(x1,x2) или v(x), функцию заданную на плоскости, следующим образом.
+1, если ниже линии AOB или на дуге AO.
v(x)=
-1, если выше линии AOB или на дуге BO.
Тогда на каждой оптимальной траектории значение u(t), управляющего параметра, в произвольный момент времени t равно v(x(t)), то есть равно значению функции v в той точке, в которой в момент времени t находится фазовая точка, пробегающая оптимальную траекторию.
