Определение достоверности и ошибок диагностики
Ошибки диагностирования возможны по следующим причинам. Во-первых, измеряемые диагностические признаки практически всегда носят случайный характер и распределены по определенным законам распределения. Поэтому при принятии решения о состоянии объекта возможно принятие ложных решений. Во-вторых, при измерении какого-либо диагностического признака измерительная система диагностирования, которая может иметь собственные состояния, вносит в принимаемые решения дополнительную ошибку.
В общем случае вероятность ошибки диагностирования Pi,j, т.е. вероятность принятия решения о j-м состоянии объекта при его реальном i-м состоянии, вычисляют по формуле [2]:
,
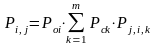где m – количество технических состояний средства диагностирования; Pоi – априорная безусловная вероятность нахождения объекта диагностирования в состоянии i; Pсk – априорная безусловная вероятность нахождения средства диагностирования в состоянии k; Pj,i,k – условная вероятность того, что средством диагностирования с состоянием k объект признан находящимся в состоянии j при реальном его состоянии i.
По статистическим данным оценку вероятности ошибки диагностирования определяют по формуле:
,
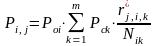где Nik – общее число испытаний системы диагностирования объекта, находящегося в состоянии i, средством диагностирования, находящимся в состоянии k; r*j,i,k – число ошибочных случаев, при которых система диагностирования при k-м своем состоянии зафиксировала j-е состояние объекта из общего количества Nik проверенных состояний i.
Вероятности Pоi и Pсk могут быть найдены либо из теоретических исследований модели объекта, либо путем его испытаний:
,
,
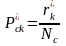где s*i – число зафиксированных случаев i-го состояния объекта вне зависимости от состояния системы диагностирования; N – общее число объектов, из которых определялись его состояния; r*k – число зафиксированных случаев k-го состояния системы диагностирования вне зависимости от состояния объекта; Nс – число испытаний системы диагностирования.
Система диагностирования, представленная в предлагаемой задаче, различает только два состояния объекта – работоспособное и неработоспособное (m = 2). Здесь возможны ошибки диагностирования только первого рода (i = 1, j = 2) и второго рода (i = 2, j = 1). Предполагается также, что сама система диагностирования тоже имеет два состояния: исправное (k = 1) и неисправное (k = 2).
Считаются также известными результаты испытаний s*1, s*2, r*1, r*2, r*121, r*122, r*211, r*212. Так, например, индекс «121» означает, что принято решение о работоспособном состоянии объекта при его реально неработоспособном состоянии работоспособной системой диагностирования. Известны также количества испытаний Nik.
Все исходные данные для расчета приведены в табл.1.7.
В задаче требуется определить достоверность и ошибку диагностики.
Таблица 1.7
Исходные данные
Первая цифра номера задания |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
s*1 |
80 |
65 |
87 |
70 |
75 |
72 |
68 |
90 |
85 |
78 |
s*2 |
16 |
22 |
6 |
5 |
8 |
7 |
9 |
9 |
10 |
11 |
Вторая цифра номера задания |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
r*1 |
66 |
55 |
81 |
88 |
92 |
68 |
84 |
85 |
90 |
58 |
r*2 |
5 |
6 |
4 |
7 |
8 |
11 |
9 |
10 |
12 |
4 |
Третья цифра номера задания |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
r*121 |
5 |
4 |
6 |
7 |
3 |
2 |
6 |
3 |
4 |
6 |
r*122 |
6 |
2 |
3 |
3 |
5 |
4 |
4 |
7 |
5 |
6 |
N2,1 = N2,2 |
40 |
35 |
45 |
42 |
52 |
48 |
45 |
55 |
46 |
38 |
Четвертая цифра номера задания |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
r*211 |
2 |
3 |
4 |
5 |
6 |
5 |
4 |
3 |
2 |
3 |
r*212 |
8 |
9 |
10 |
11 |
12 |
5 |
8 |
7 |
9 |
6 |
N1,1 = N1,2 |
60 |
65 |
48 |
55 |
60 |
58 |
49 |
62 |
56 |
47 |
Определяем общее количество испытаний для определения безусловных вероятностей:
N = s*1 + s*2; Nс = r*1 + r*2.
В общем случае, учитывая все четыре возможных варианта ошибок, получим суммарную ошибку в виде:
.
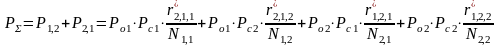Определяем безусловные вероятности:
,
,
,
.
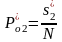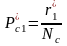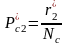Рассчитываем численные значения и определяем суммарную ошибку диагностики P.
Достоверность диагностики:
D = 1 - P.