7 Пример решения расчетно-графической работы

Задание

1. Определить передаточные функции разомкнутой системы, замкнутой системы по управлению и возмущению.

2. Проверить устойчивость замкнутой системы по критериям устойчивости Гурвица и Михайлова.

3. Определить запас устойчивости разомкнутой системы по фазе с помощью критерия устойчивости Найквиста.

Схема 7

Таблица 2 – Данные для расчета: вариант 3 (таблица 1)

k1	T1	τ 1	k01	k2	T2	τ 2	k02	k3	τ 3	k 4	T4	τ 4
10	1	0,6	0	0,9	0,5	0,3	1	1	0	0,5	0	0

Решение

1. Определим передаточные функции разомкнутой системы, замкнутой системы по управлению и возмущению.

Сначала преобразуем исходную схему:

W₅=W₃•W₂ , (1)

, (2)

Передаточная функция разомкнутой системы:

, (3)

Подставим значения (таблица 1) в формулы (4), (5) ,(6) ,(7).

, (4)

, (5)

, (6)

. (7)

Для определения передаточной функции разомкнутой системы подставим значения, полученные из формул (4), (5), (6), (7) в формулу (3):

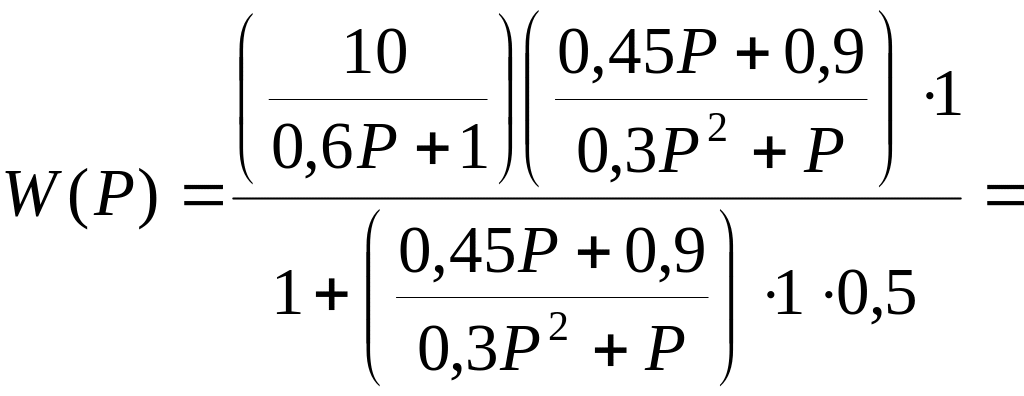
( 8)

Определим передаточную функцию замкнутой системы по управлению:

. (9)

Определим передаточную функцию замкнутой системы по возмущению:

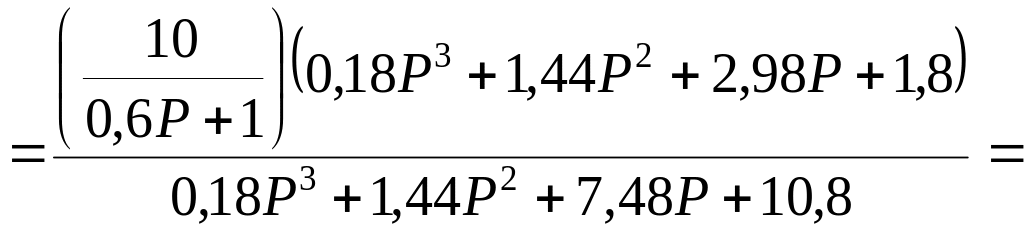
. (10)

2. Определим устойчивость САУ по критерию Гурвица. Запишем характеристическое уравнение замкнутой системы по управлению. Для этого приравняем к нулю знаменатель передаточной функции по управлению.

а₀Р³+а₁Р²+а₂Р+а₃=0, (11)

0,18Р³+1,44Р²+7,48Р+10,8=0.

При положительных коэффициентах критерий Гурвица сводится к проверке следующего неравенства:

∆3 = а₃ · ∆2 = а₃· , (12)

10,8· .

Определим критический коэффициент усиления замкнутой системы по формуле:

.

Проверим устойчивость системы автоматического управления по критерию Михайлова.

Для построения годографа Михайлова в характеристическом полиноме замкнутой системы автоматического управления заменим оператор Р на j. Полученное комплексное число представим в алгебраической форме:

, (13)

, (14)

, (15)

(16)

Заменяя  числом от 0 до ∞, определим значение функции для построения графика на комплексной плоскости. На первом этапе найдем точки пересечения графика с действительной и мнимой осью.

Точки пересечения с осью jV() можно определить, опираясь на условие, что U()=0, то есть 10,8-1,44²=0 → .

.

Аналогичным образом находим точки пересечения с осью U().

V()= 0, т.е. 7,48 - 0,18³ = 0,

₁=0 7,48 - 0,18²=0,

₂= ±6,44,

U₁=10,8-1,44•0²=10,8,

U₂=10,8-1,44•6,44²=-49,04

Таблица 3 – Данные расчетов для построения годографа Михайлова

	0	0, 05	0, 1	0,15	0, 2	0, 25	0, 3
U()	4,999	4, 972	4, 906	4, 806	4,67	4, 514	4, 332
V()	0	-0, 28	-0, 57	-0, 84	-1,09	-1, 33	-1, 547

Рисунок 1 – Годограф Михайлова

По расположению характеристической кривой (рисунок 1) можно сделать вывод: годограф Михайлова для замкнутой системы, представленной уравнением третьего порядка, при изменении частоты  от 0 до ∞ начинается на положительной вещественной полуоси и, вращаясь против часовой стрелки, проходит последовательно 3 квадранта, поэтому данная система является устойчивой.

По годографу графически определяем критический коэффициент передачи.

,

где S-коэффициент передачи,

S₀- коэффициент запаса.

Если значения максимального коэффициента передачи, найденные по критериям Гурвица и Михайлова, совпадают, то исследование системы на устойчивость проведено верно.

3. Определим запас устойчивости разомкнутой системы по фазе. Для этого воспользуемся критерием Найквиста.

Передаточная функция разомкнутой системы имеет вид:

. (17)

Заменим оператор Р на j и выделим действительную и мнимую части.

;

.

Минимальный угол γ (рисунок 2), образуемый радиусом, проходящим через точку пересечения годографа W(j) c окружностью радиусом (0-1) с центром в начале координат, и действительной отрицательной полуосью, называют запасом устойчивости по фазе.

Рисунок 2 – Годограф Найквиста

Из годографа видно, что γ=68º.