12. Сложное сопротивление

12.1. Понятие о сложном сопротивлении

На практике во многих случаях элементы конструкций подвергаются действию сил, вызывающих одновременно несколько деформаций. В таких случаях имеет место сложное сопротивление.

Все задачи на сложное сопротивление решаются методом сложения действующих сил, напряжений и деформаций. В процессе расчета определяют напряжения и деформации, соответствующие простым нагружениям, а затем их суммируют.

12.2. Косой изгиб

Косой изгиб представляет собой деформацию такого изгиба, при котором плоскость действия нагрузок не совпадает ни с одной из главных плоскостей инерции (рис.12.1).

Условие прочности при косом изгибе:

, (12.1)

где и – соответственно изгибающие моменты в данном сечении относительно осей Y и Z (рис.12.1)

и - моменты сопротивления данного сечения относительно осей Y и Z. Положение нейтральной линии характеризуется угловым коэффициентом

, (12.2)

где и - моменты инерции сечения относительно осей Y и Z.

Рис. 12.1

Поскольку угол наклона силовой линии определяется выражением

, то .

Условие жесткости

, (12.3)

где - полный прогиб стержня,

и - прогиб стержня соответственно в плоскостях,

- допускаемое значение полного прогиба.

12.3. Внецентренное растяжение (сжатие)

Внецентренное растяжение (сжатие) представляет собой случай сложного нагружения, при котором стержень растягивается (сжимается) силами, параллельными оси стержня так, что их равнодействующая не совпадает с осью бруса (рис.12.2).

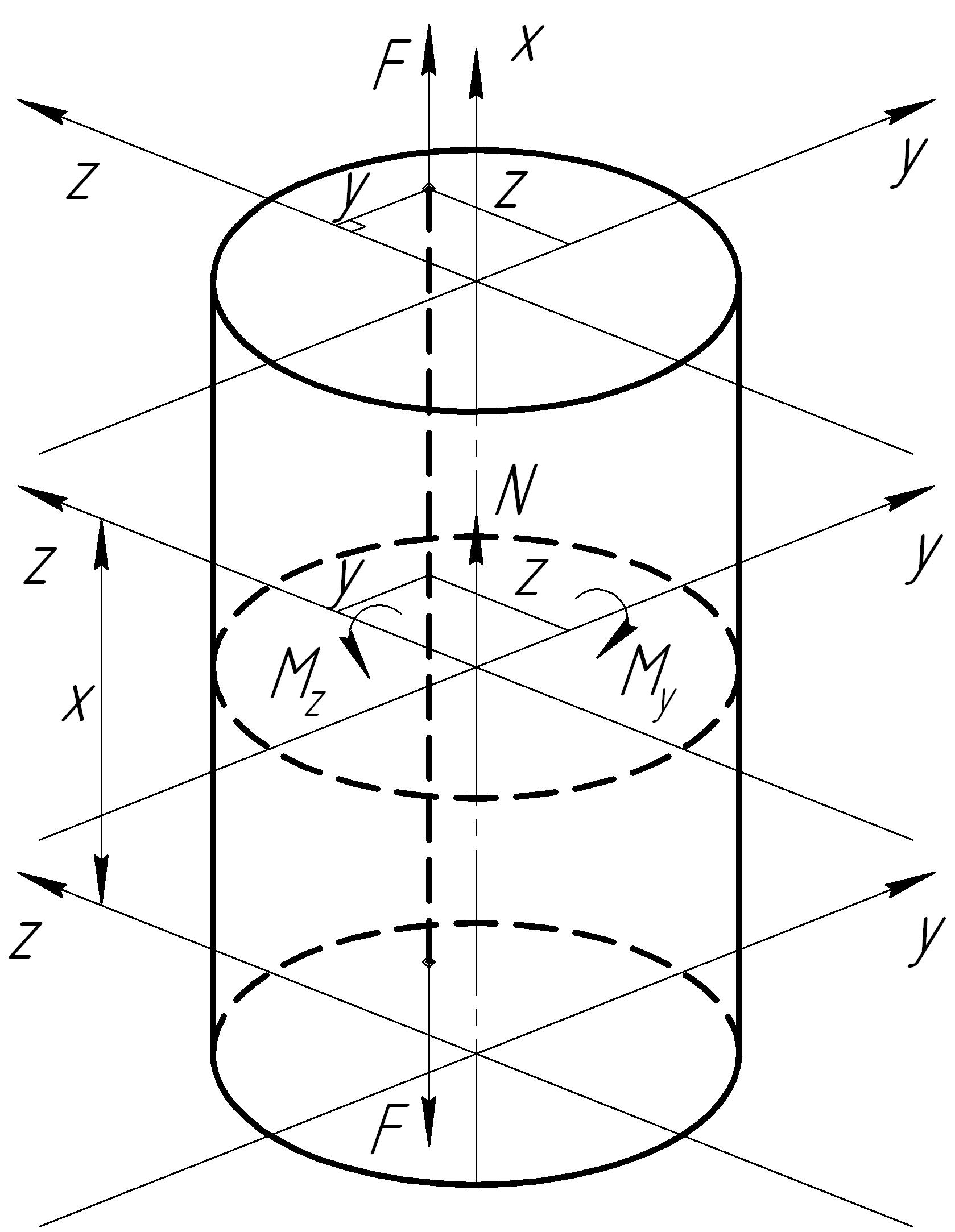
Рис. 12.2

Максимальное напряжение при внецентренном растяжении (рис.12.2)

, (12.4)

где – нормальная сила, Н

– площадь поперечного сечения стержня, мм².

При действии на стержень одной силы , параллельной оси стержня и пересекающей поперечное сечение в точке D с координатами и , будет иметь

, (12.5)

Условие прочности

,

где - допускаемое напряжение.

12.4. Изгиб с кручением Условие прочности при изгибе с кручением круглоёго стержня

, (12.6)

где - эквивалентное напряжение, МПа

- момент сопротивления сечения, мм³

– расчетный момент, Нмм.

, (12.7)

где и – соответственно изгибающий и крутящий моменты.

При применении IV-ой теории прочности

, (12.8)

Диаметр круглого вала, подверженного изгибу и кручению, равен

, (12.9)

где - допускаемое напряжение, МПа.

- осевой момент сопротивления сечения стрежня.

12.5. Методика решения задач

Задача 12.5.1.Кирпичный столб высотой м, весом кН, квадратного поперечного сечения ( м, м) нагружен своим собственным весом и поперечным равномерно распределённым давлением, равным Н/м (рис. 12.3). Определить величину наибольшего и наименьшего сжимающих напряжений в основании столба.

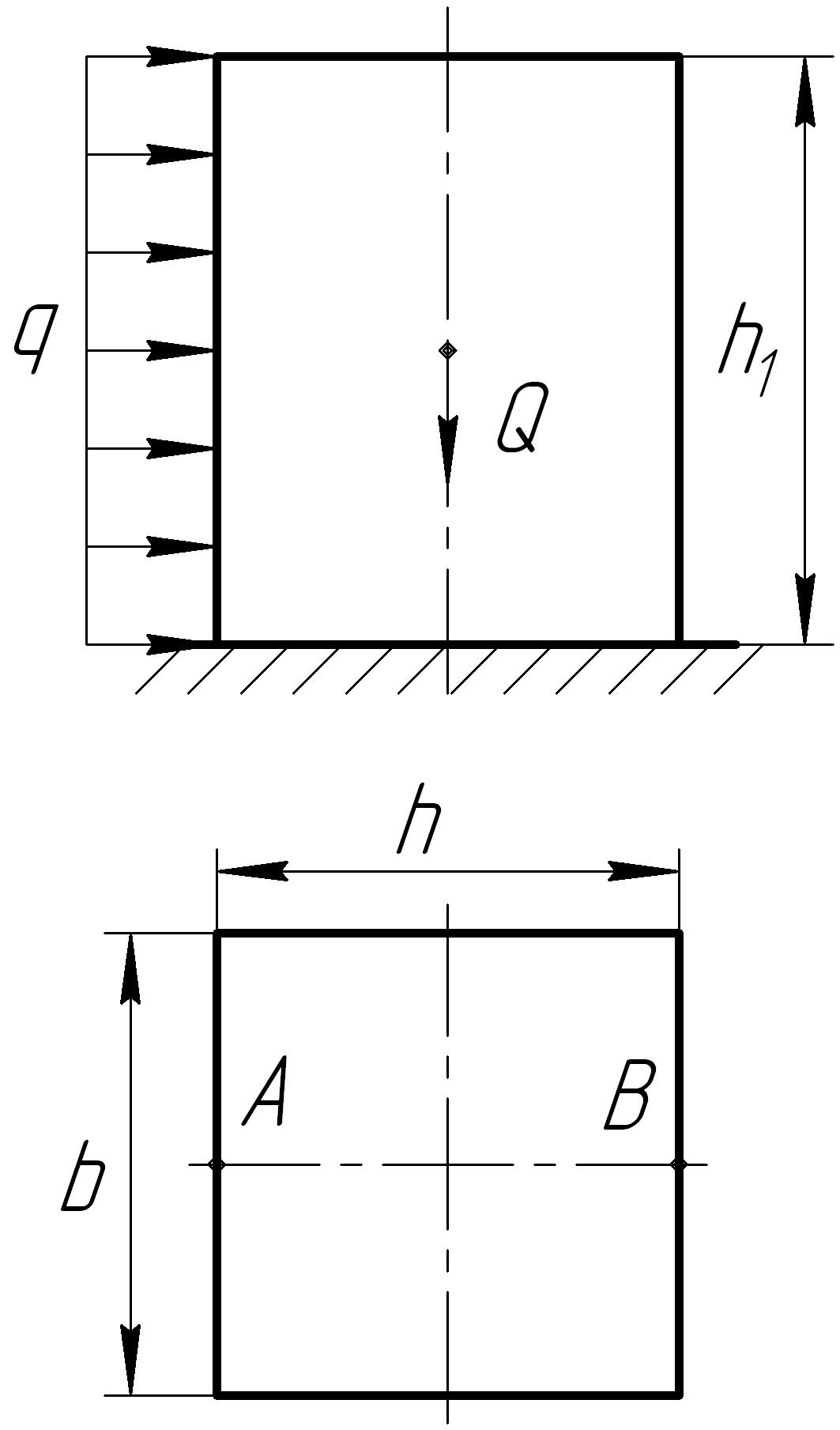
Рис. 12.3

Решение:

I. Определить напряжения в точке А

;

,

Н/мм²

2. Определение напряжения в т. B.

Н/мм²

Задача 12.5.2. Деревянная балка прямоугольного поперечного сечения шириной мм, высотой мм шарнирно оперта по концам и нагружена посередине пролета м сосредоточенной силой кН. Плоскость действия нагрузки составляет угол с вертикальной плоскостью, проходящей через ось балки.

Определить положение нейтральной линии и наибольшее сжимающее напряжение в поперечном сечении балки. Определить полный прогиб по величине и направлению (рис. 12.4 а)

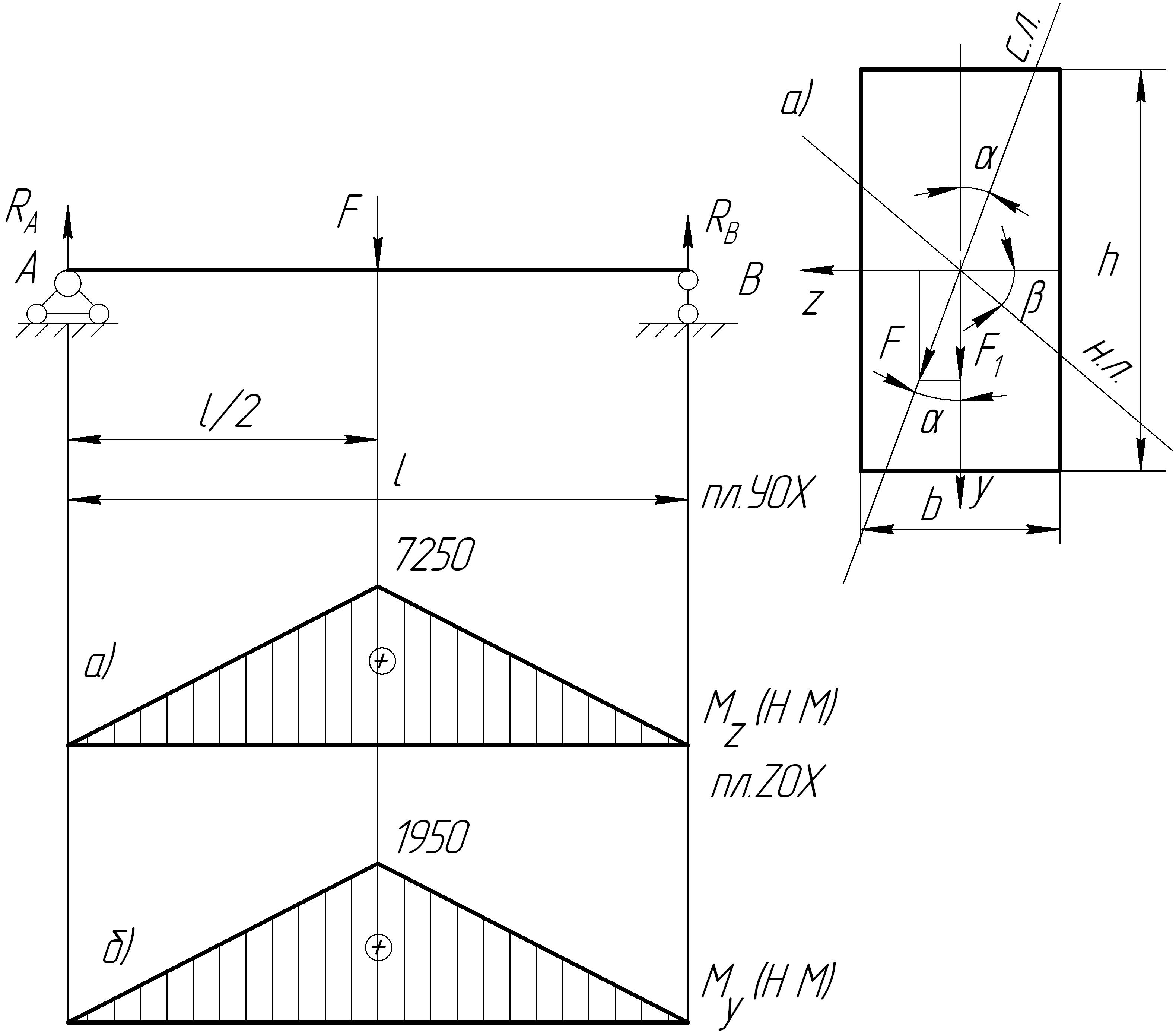
Рис. 12.4

Решение:

1. Определение угла наклона нейтральной линии к оси Z

;

.

2. Наибольшее сжимающее напряжение будет в точке С

,

где – изгибающий момент в вертикальной плоскости

– изгибающий момент в горизонтальной плоскости

Расчетная схема в вертикальной плоскости УСХ – на рис. 12.4, а

Сила F₁, действующая в вертикальной плоскости:

Н.

Максимальный изгибающий момент в вертикальной плоскости

Нм.

Расчетная схема в горизонтальной плоскости на рис. 12.4.б

Сила F₂, действующая в горизонтальной плоскости

Н.

Максимальный изгибающий момент в горизонтальной плоскости

Нм.

Момент сопротивления относительно осей Z и Y:

мм³

мм³

Максимально сжимающее напряжение прогиба в точке A:

Н/мм²

3. Определение наибольшего прогиба посередине пролета

мм; мм

для дерева Н/мм².

мм.

Направление прогиба составляет с осью Y угол

.

Задача 3. Определить диаметр вала косозубой зубчатой передачи при Н, м, Н/мм² (рис.12.5)

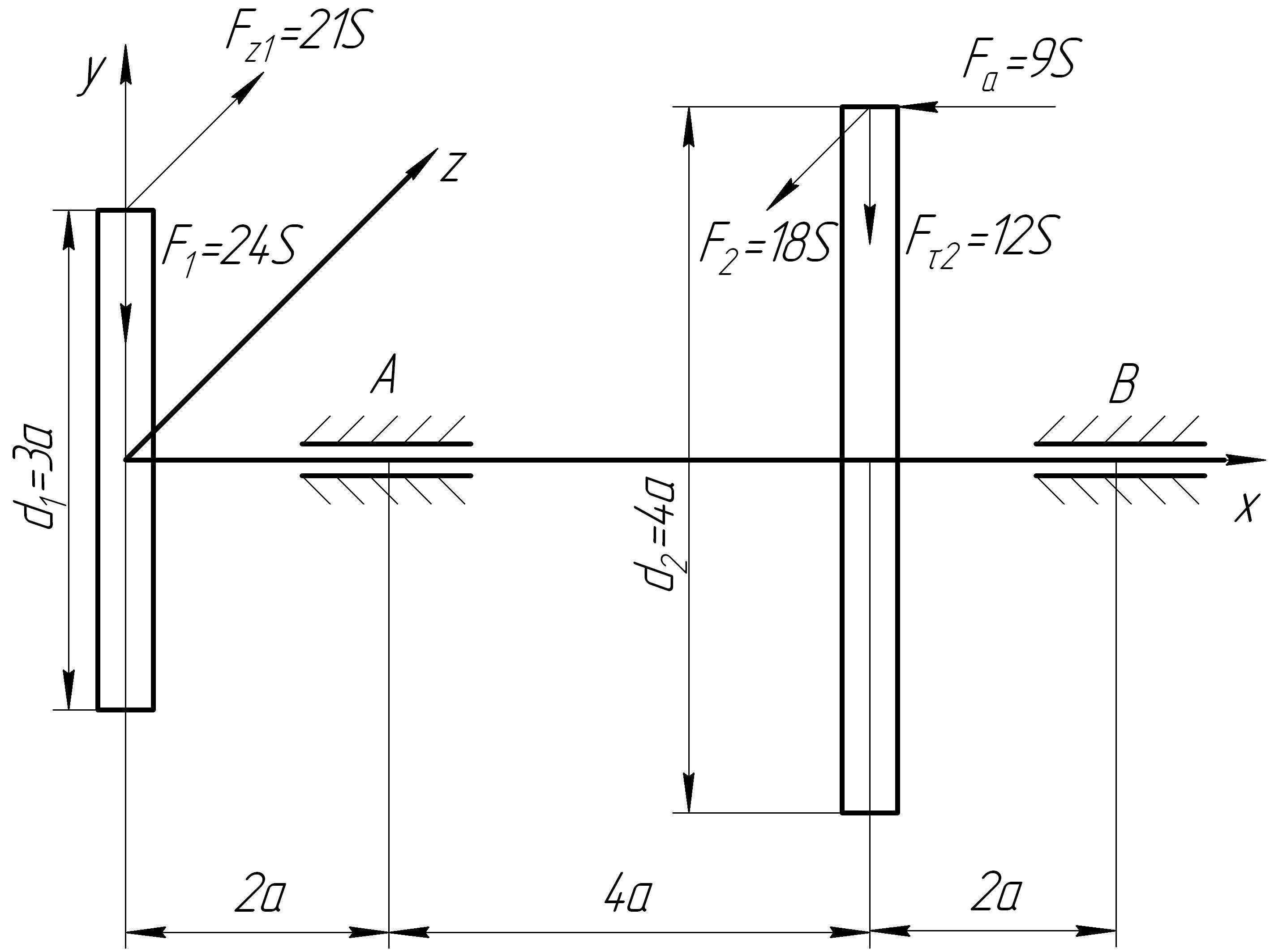
Рис. 12.5

I. Составление расчетной схемы вала в двух плоскостях: вертикальной и горизонтальной (рис. 12.6, а, б.)

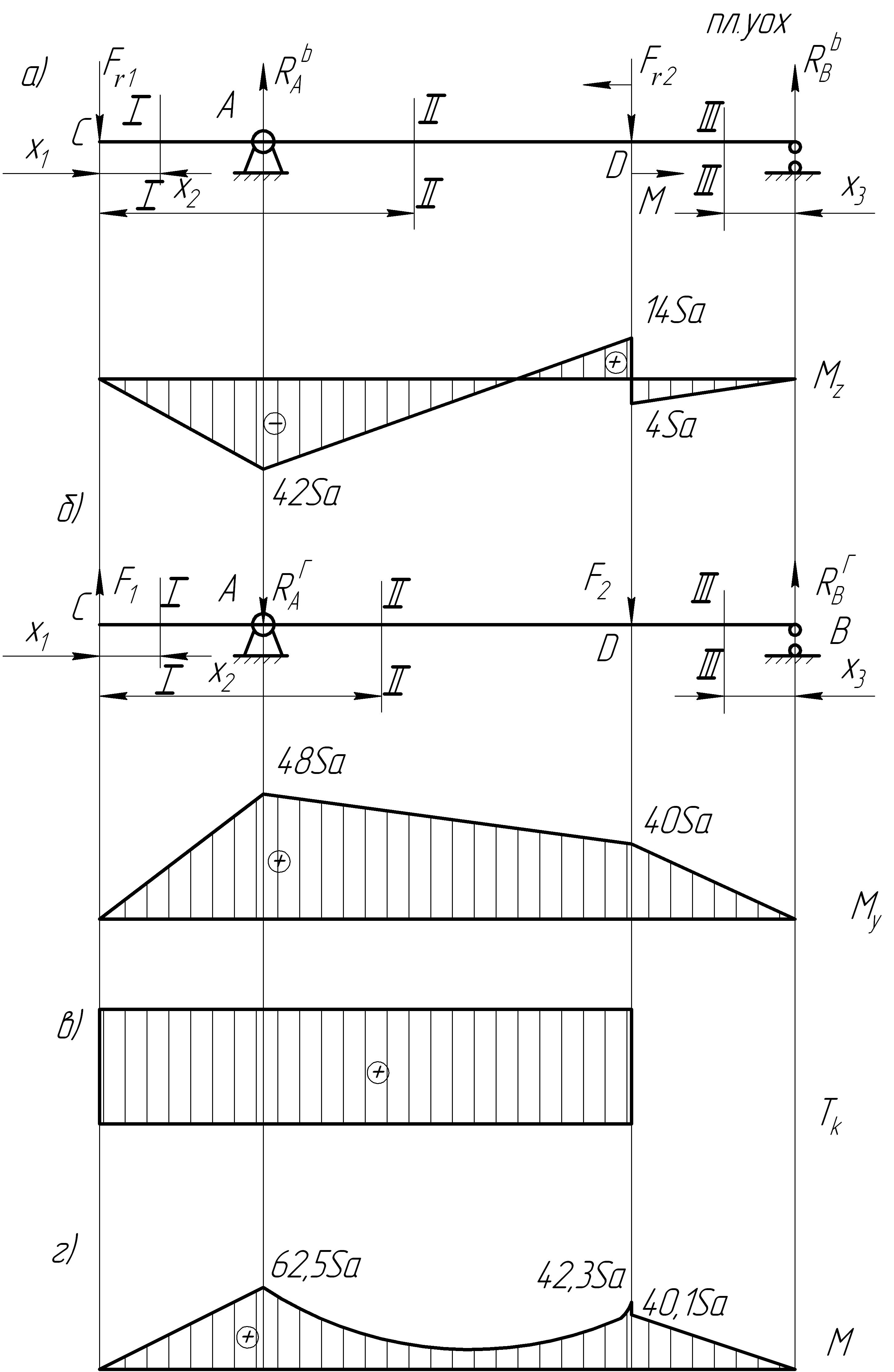
Рис. 12.6

2. Крутящие моменты.

;

3. Сосредоточенный момент

.

4. Определение изгибающих моментов и построение эпюры в вертикальной плоскости:

а) Реакции в опорах A и B определяем из условий: ;

;

Проверка: , .

Реакции определены правильно.

б) Построение эпюры изгибающих моментов

Участок 1 – 2:

;

Участок 2 – 3:

Участок 3 – 4:

;

5. Определение изгибающих моментов и построение эпюры в горизонтальной плоскости

а) Реакции в опорах A и B определены из условий ;

;

откуда

;

.

Проверка:

Реакции определены правильно.

б) Построение эпюры изгибающих моментов.

Участок 1 – 2:

При ; при

Участок 2 – 3:

При

При

Участок 3 – 4:

При ; при

6. Определение суммарных изгибающих моментов и построение их эпюры (рис. 12.6, г).

Суммарный момент

В сечении 1:

В сечении 2:

В сечении 3:

В сечении 4:

Следовательно, наибольший суммарный момент действует в сечении 2 и равен

7. Определение крутящих моментов. Вал скручивается на участке I – 3 двумя противоположно направленными моментами и (рис. 12.6, в)

Крутящий момент

8. Определение расчетного (или эквивалентного) момента для опасных сечений по III и IV теории прочности.

По III теории прочности:

Нм

По IV теории прочности:

Нм

9. Определение диаметра вала:

Условие прочности при изгибе с кручением

Для круглого сечения

Тогда

Допускаемое напряжение

Н/мм²

Примем: Н/мм²

Диаметр вала при расчете по III теории прочности:

мм.

Округляем по ГОСТ 6639-69 мм.

Задача 12.5.4

Рассчитать на статистическую прочность тихоходный вал (рис. 12.7) цилиндрического зубчатого редуктора с прямозубыми колесами, если мощность на этом валу кВт, частота вращения вала в минуту об/мин, диаметр делительной окружности зубчатого колеса мм. Длина пролета мм, ширина колеса мм. Материал вала – сталь 45.

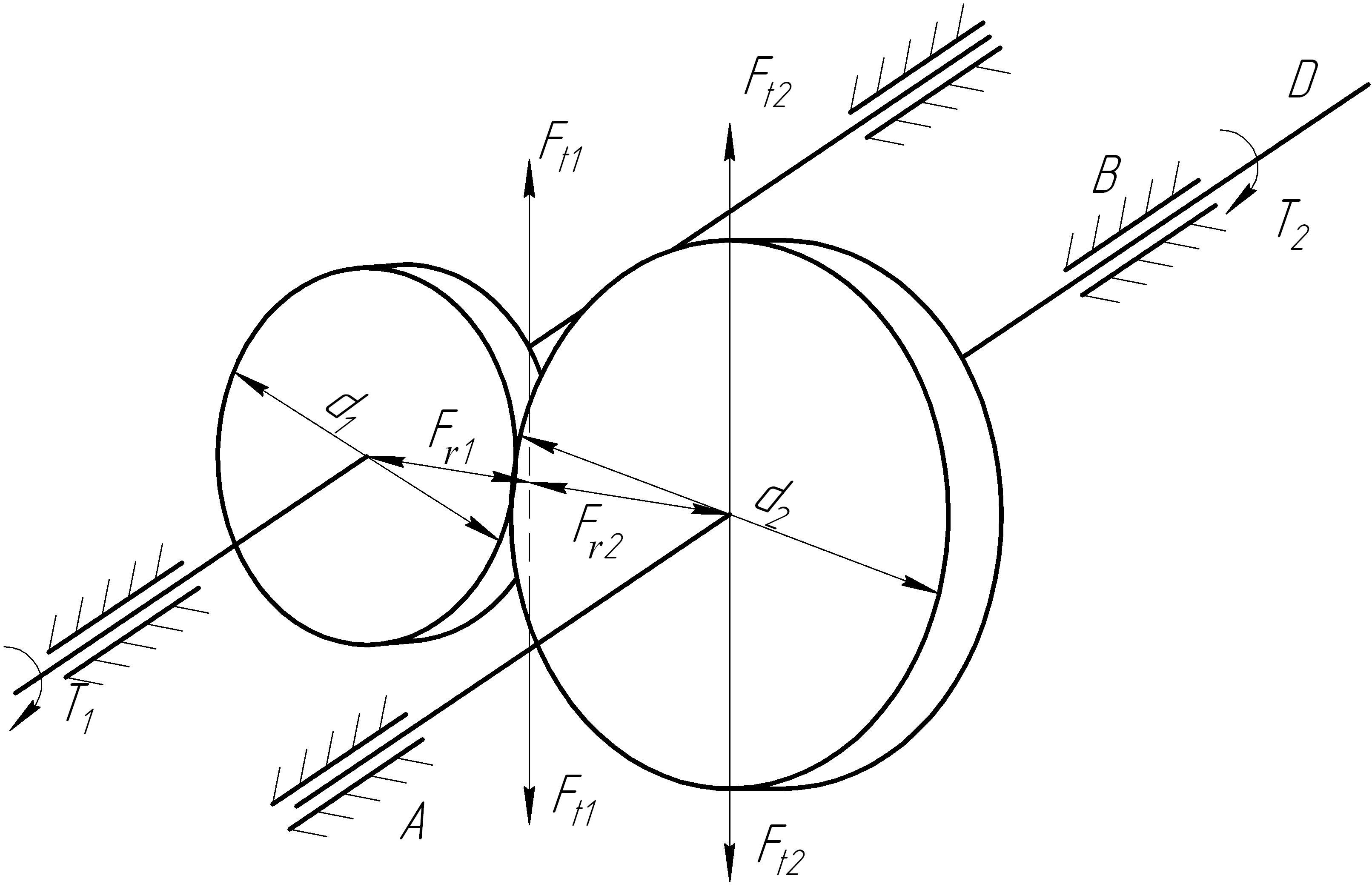
Рис. 12.7

Решение:

I. Расчет выходного конца вала на кручение.

где - крутящий момент на валу колеса, Нмм

- допускаемое напряжение при расчете на кручение, Н/мм²

Для валов из сталей ст.5, ст.6., ст.45 принимают при определении диаметра выходного конца Н/мм²

Примем Н/мм²

Крутящий момент в сечении вала на участке СD определим из условия . Отсюда .

,

где - угловая скорость тихоходного вала, рад/с

рад/с

Тогда

Нм Нмм

Диаметр выходного конца вала

мм.

Полученный результат округляем до ближайшего значения из стандартного ряда. В данном случае принимаем мм.

2. Определение сил, действующих в зацеплении зубчатых колес

Окружная сила

Н

Радиальная сила

,

где - угол зацепления.

Тогда Н.

3. Составление расчетной схемы тихоходного вала.

Расчетная схема тихоходного вала имеет вид (рис. 12.8).

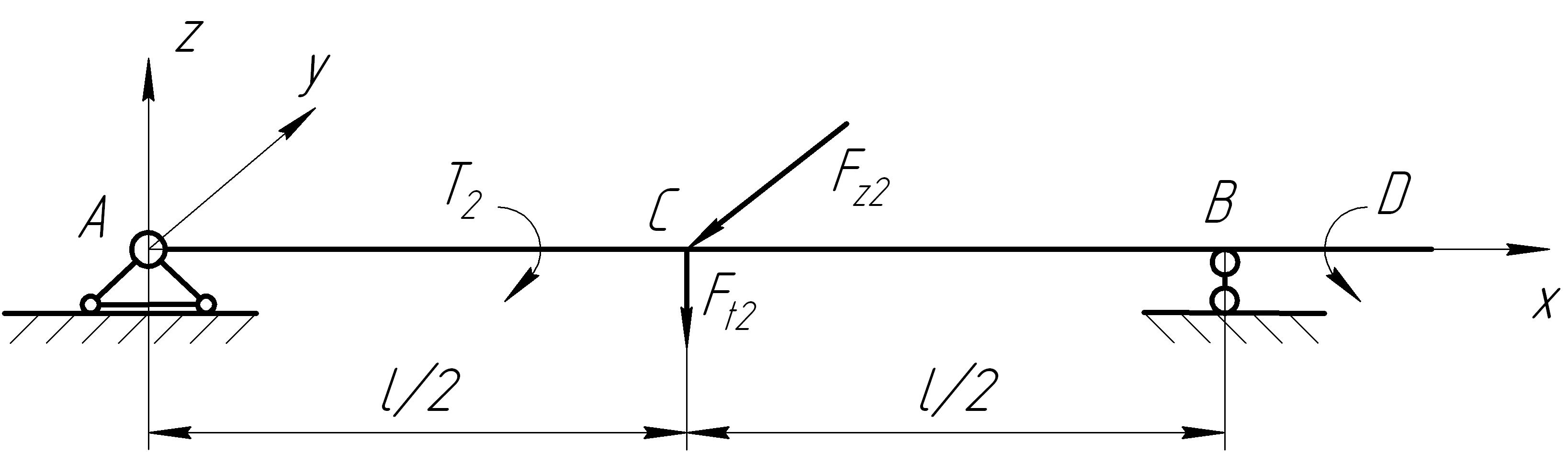
Рис. 12.8

4. Построение эпюры изгибающих моментов в вертикальной плоскости (в плоскостях ХОY) (рис. 12.9, а).

Реакции опор и определяются из условий ;

В данном случае

Н.

Изгибающий момент в сечении I – I (участок АС) равен

;

При

Нмм.

Изгибающий момент в сечении II – II (участок СВ)

;

При

Нмм.

По этим данным строится эпюра (рис. 12.9, а)

5. Построение эпюры изгибающих моментов в горизонтальной плоскости (в плоскости XOZ) и эпюры крутящих моментов.

Реакции опор и определяются из условий

;

В данном случае

Н.

Изгибающий момент в сечении I – I (участок АС)

;

При

Нмм

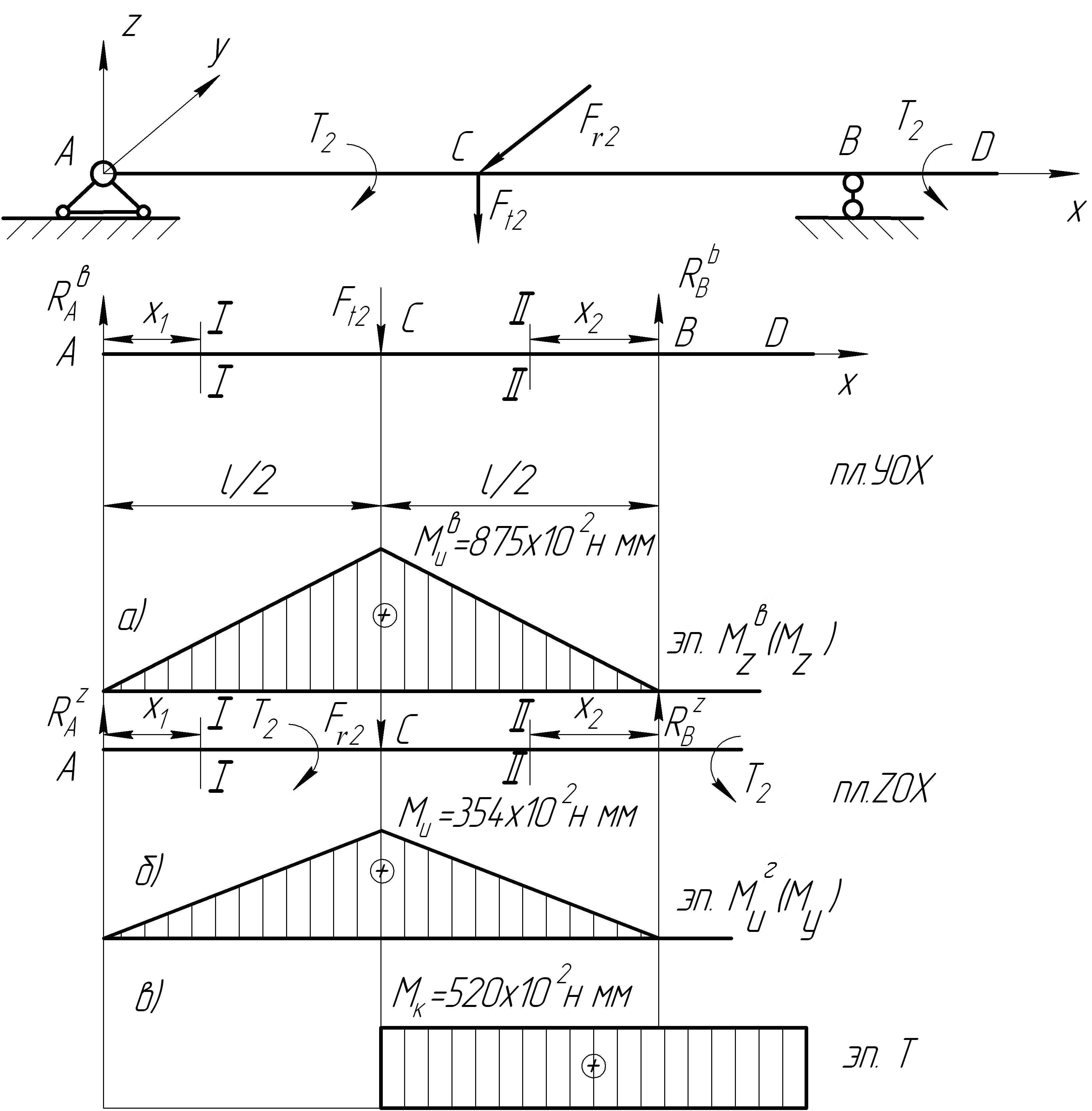
Рис. 12.9

Изгибающий момент в сечении II – II (участок СВ)

,

При

Нмм

Крутящий момент на участке вала СD:

Нмм

По полученным результатам производится построение эпюр и (рис. 12.9, б)

6. Определение суммарного изгибающего момента

Нмм

7. Определение расчетного момента по третьей теории прочности

Нмм

8. Определение диаметра вала в опасном сечении:

,

где - допускаемое напряжение на изгиб вала, Н/мм²

Для вала из стали 45 Н/мм².

Тогда

мм.

Примем по ГОСТ мм.

На основании результатов решении этой задачи и подбора подшипников качения (шариковые, радиальные однорядные № 110) производят конструирование вала и производят подбор шпонок.