
- •5. Порядок решения задач
- •5.1. Составление расчетной схемы
- •5.2. Статически определимая система и нахождение реакций опор
- •5.3. Определение количества участков
- •5.4. Составление аналитического выражения внутренних силовых
- •5.5. Построение эпюр внутренних силовых факторов по составленных аналитическим выражениям
- •5.6. Проверка правильности построения эпюр
- •5.7. Определение опасного сечения
- •6. Задачи для выполнения практических работ
- •7. Примеры решения задач
- •8. Напряженное и деформированное состояние при сложном нагружении. Гипотезы предельных состояний
- •9. Потенциальная энергия деформаций, определение перемещений. Расчет статически неопределимых систем
- •10. Устойчивость деформированного состояния
- •11. Местные и контактные напряжения. Прочность при переменных нагрузках
- •12. Сложное сопротивление
- •12.1. Понятие о сложном сопротивлении
- •12.2. Косой изгиб
- •12.3. Внецентренное растяжение (сжатие)
- •Максимальное напряжение при внецентренном растяжении (рис.12.2)
- •12.4. Изгиб с кручением Условие прочности при изгибе с кручением круглоёго стержня
- •12.5. Методика решения задач
- •13. Основы расчета на выносливость
- •Пульсационный (отнулевой) цикл (частный случай ассиметричного цикла)
- •13.1. Методика решения задач
- •14. Продольный изгиб
- •14.1. Методика решения задач
- •14.2. Задачи для самостоятельного решения
- •Наталья Александровна Лазуткина Ольга Григорьевна Кокорева
- •280101.65 «Безопасность жизнедеятельности в техносфере».
- •Муромский институт (филиал)
7. Примеры решения задач
Пример 1.
Абсолютно жесткий
брус АС, нагруженный силой
![]() кН, шарнирно закреплен в точке А и
подвешен на двух стальных стержнях с
сечениями
кН, шарнирно закреплен в точке А и
подвешен на двух стальных стержнях с
сечениями
![]() см2
и
см2
и
![]() см2 (рис. 7.1, а). Найти напряжения в
стержнях. Определить допускаемую
нагрузку
см2 (рис. 7.1, а). Найти напряжения в
стержнях. Определить допускаемую
нагрузку
![]() и предельно допускаемую нагрузку
и предельно допускаемую нагрузку
![]() при
при
![]() МПа,
МПа,
![]() МПа и
МПа и
![]() .
.
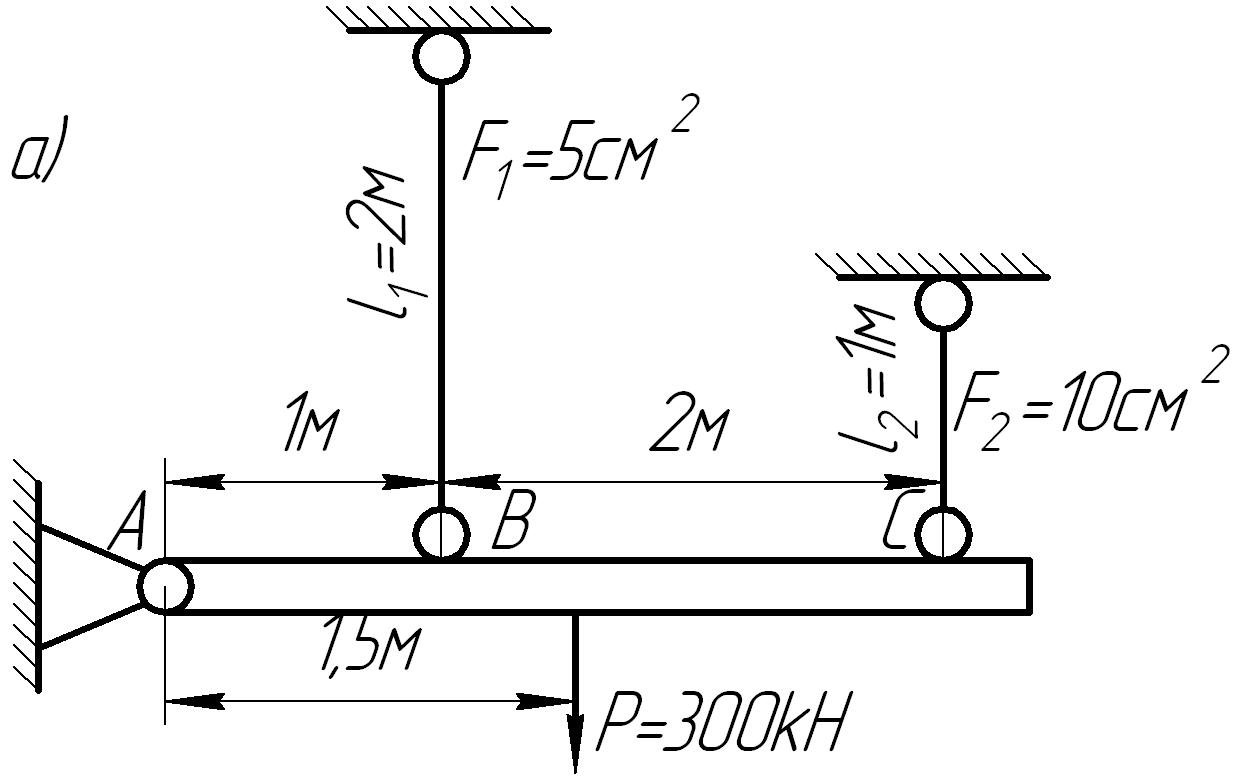

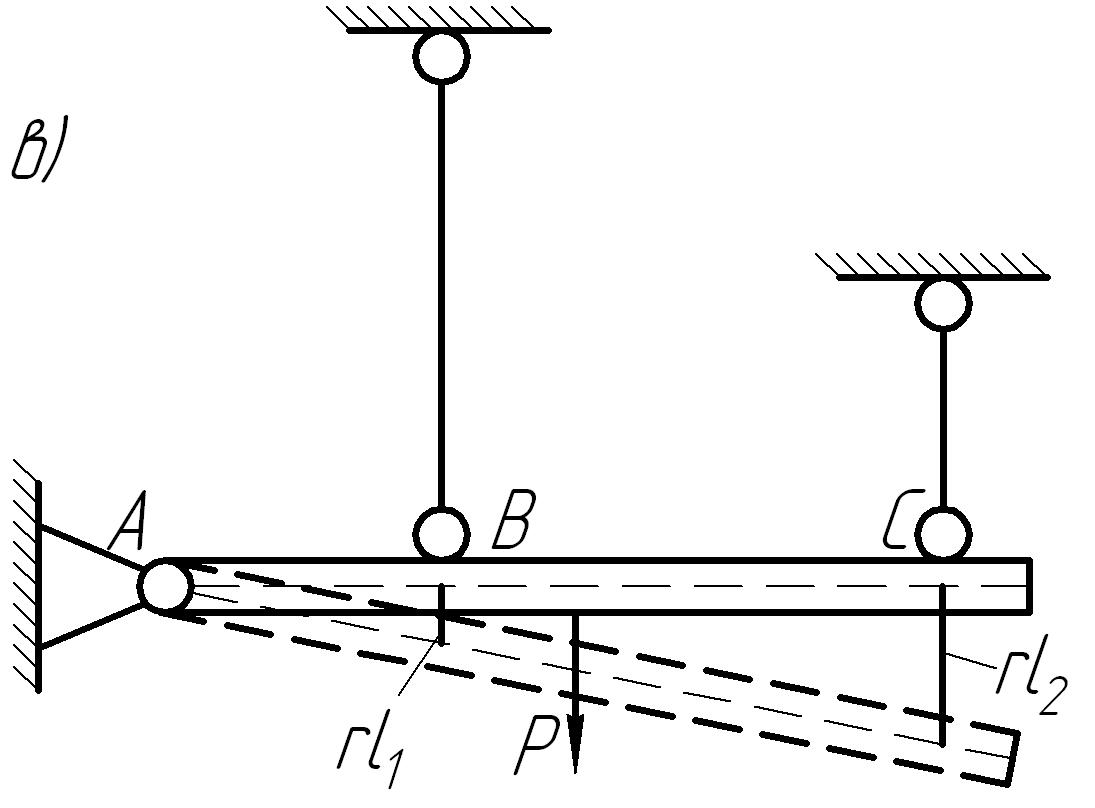
в)
Рис. 7.1
Решение.
Отбросив мысленно левый и оба верхних
опорных шарнира и заменив их влияние
на конструкцию опорными реакциями
![]() ,
,
![]() и усилиями в стержнях
и усилиями в стержнях
![]() ,
,
![]() (рис. 7.1, б). Составим уравнения равновесия
бруса:
(рис. 7.1, б). Составим уравнения равновесия
бруса:
![]() ;
;
![]() ;
;
![]() .
.
В три уравнения равновесия входят четыре неизвестные силы, и, следовательно, задача является один раз статически неопределимой. Для составления дополнительного уравнения рассмотрим деформацию конструкции.
В результате
удлинения стержней брус (который
предполагается абсолютно жестким)
повернется вокруг шарнира А, оставаясь
прямым (рис. 7.1, в). Перемещение шарнира
В равно удлинению
![]() первого (левого) стержня, а перемещение
шарнира С – удлинению
первого (левого) стержня, а перемещение
шарнира С – удлинению
![]() ,
второго (правого) стержня. Из подобия
треугольников (рис. 7.1, в) находим:
,
второго (правого) стержня. Из подобия
треугольников (рис. 7.1, в) находим:
![]() ,
,
откуда:
![]() .
.
Но на основании закона Гука:
![]() ,
а
,
а
![]()
и, следовательно:
![]() ,
,
откуда:
![]() .
.
Подставив найденное значение в последнее из уравнений равновесия:
![]() ,
,
откуда:
![]() кН,
кН,
![]() кН.
кН.
Напряжения в стержнях:
![]() МПа;
МПа;
![]() МПа.
МПа.
Найдем теперь
допускаемое значение
силы
.
При
![]() нормальные напряжения в более напряженном
втором стержне
нормальные напряжения в более напряженном
втором стержне
![]() МПа, а не 146 МПа, как при
кН.
МПа, а не 146 МПа, как при
кН.
Следовательно:
![]() кН.
кН.
При предельном
состоянии системы, соответствующем
исчерпанию ее грузоподъемности,
нормальные напряжения в поперечных
сечениях обоих стержней равны
![]() ,
а следовательно:
,
а следовательно:
![]() кН и
кН и
![]() кН.
кН.
Из условия равновесия
(![]() )
находим значение предельной нагрузки:
)
находим значение предельной нагрузки:
![]() кН.
кН.
По формуле находим предельно допускаемую нагрузку:
![]() кН.
кН.
Пример 2. Растяжение-сжатие прямолинейного стержня
Стальной стержень (рис. 7.2) ( МПа) находится под действием внешних сил Р1, Р2 и Р3.
Дано:
![]() м,
м,
![]() м,
м,
![]() см2,
см2,
![]() кН,
кН,
![]() кН,
кН,
![]() кН,
кН,
![]() МПа.
Требуется построить эпюры продольных
сил
,
нормальных напряжений
и перемещений
МПа.
Требуется построить эпюры продольных
сил
,
нормальных напряжений
и перемещений
![]() по длине стержня.
по длине стержня.
Решение. Выбираем положительное направление оси бруса с учетом правила знаков на растяжение и сжатие: если стержень растягивается принимаем знак «+», если сжимается – «-». Разделим брус на три участка I – III, границы которых определяются точками приложения сил и изменением поперечного сечения стержня.
Для построения эпюры продольных сил проводим сечения в пределах каждого участка и рассматриваем равновесие нижней части бруса; продольные силы предварительно направляем от сечения, считая, что участок бруса работает на растяжение (рис. 7.2, а).
Получим
для участка I:
![]() кН;
кН;
для участка II:![]() ,
откуда
,
откуда
![]() кН;
кН;
для участка III:
![]() ,
,
![]() кН.
кН.
Анализируя эпюру продольных сил, приходим к выводу, что на первом и втором участках брус работает на растяжение, на третьем участке – на сжатие.
С помощью полученных данных строим эпюру продольных сил , рис. 7.2, б.
Для построения эпюры нормальных напряжений определяем напряжение на каждом участке:
![]() Н/см2 = 21,4
МПа,
Н/см2 = 21,4
МПа,
![]() Н/см2 = 32,1
МПа,
Н/см2 = 32,1
МПа,
![]() Н/см2 = - 17,8
МПа.
Н/см2 = - 17,8
МПа.
С помощью полученных
данных строим эпюру нормальных напряжений
,
рис. 7.2, в. Значение
![]() составляет:
составляет:
![]() МПа.
МПа.
Проверяем условие
прочности:
![]() ,
,
![]() .
Условие выполняется.
.
Условие выполняется.
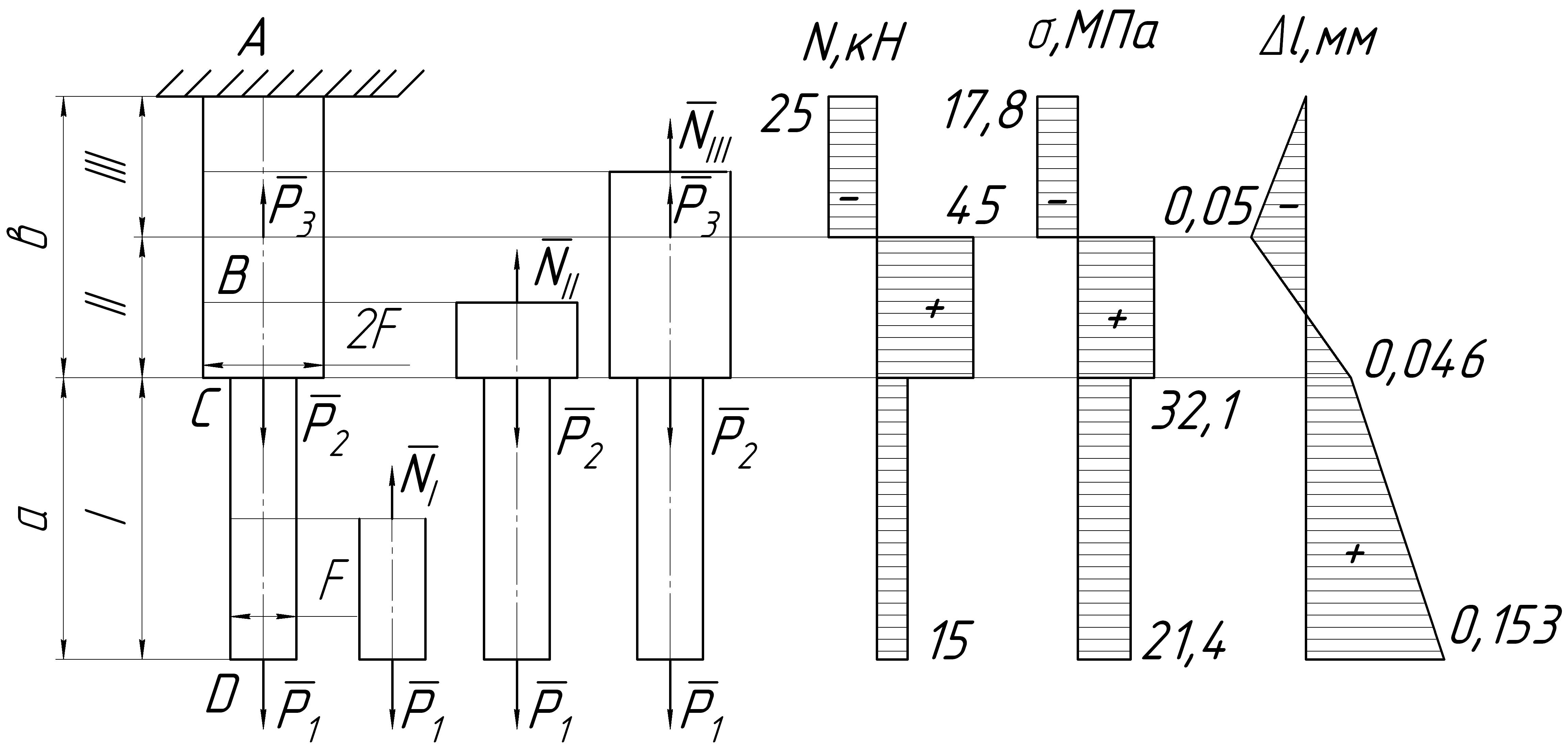
Рис. 7.2. Расчетная схема стержня (а), эпюры нормальных сил (б),
нормальных напряжений (в) и перемещений (г)
Построение эпюры перемещений начинаем от заделки стержня. Перемещение сечения А равно 0. Тогда перемещение сечения В на участке III равно
 мм;
мм;
перемещение сечения С на участке II
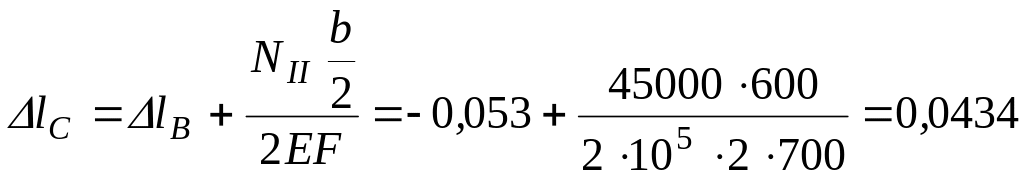 мм;
мм;
перемещение торца бруса D
 мм.
мм.
По полученным значениям строим эпюру , рис. 7.2, г.
Пример 3. Кручение стержня круглого поперечного сечения
Требуется: а) построить эпюру крутящих моментов; б) при заданном значении допускаемого касательного напряжения определить диаметр вала и округлить его до числа кратного 5 мм; в) построить эпюру углов закручивания; г) найти наибольший относительный угол закручивания на 1 м.
К стальному валу приложено три момента (рис. 7.3).
Дано:
![]() м,
м,
м,
м,
![]() м,
м,
![]() Нм,
Нм,
![]() Нм,
Нм,
![]() Нм,
Нм,
![]() МПа.
МПа.
Решение. Разбиваем вал на три участка, границами которых служат точки приложения крутящих моментов. Построение эпюры крутящих моментов начинаем от свободного конца вала, рис. 7.3.
Для построения эпюры крутящих моментов применяем метод сечений. При этом применяем следующее правило знаков: крутящий момент считается положительным, когда он направлен по часовой стрелке, если смотреть на оставленную часть бруса со стороны проведенного сечения.
Определяем крутящий момент для каждого участка:
участок I:
![]() Нм;
Нм;
участок II:
![]() Нм;
Нм;
участок III:
![]() Нм.
Нм.
С помощью полученных
данных строим эпюру крутящих моментов
![]() (см. рис. 4, б), на основании которой
получаем
(см. рис. 4, б), на основании которой
получаем
![]() Нм.
Нм.
С помощью полученного
значения
![]() и по заданному значению допускаемого
касательного напряжения, определяем
диаметр вала по следующим формулам.
и по заданному значению допускаемого
касательного напряжения, определяем
диаметр вала по следующим формулам.
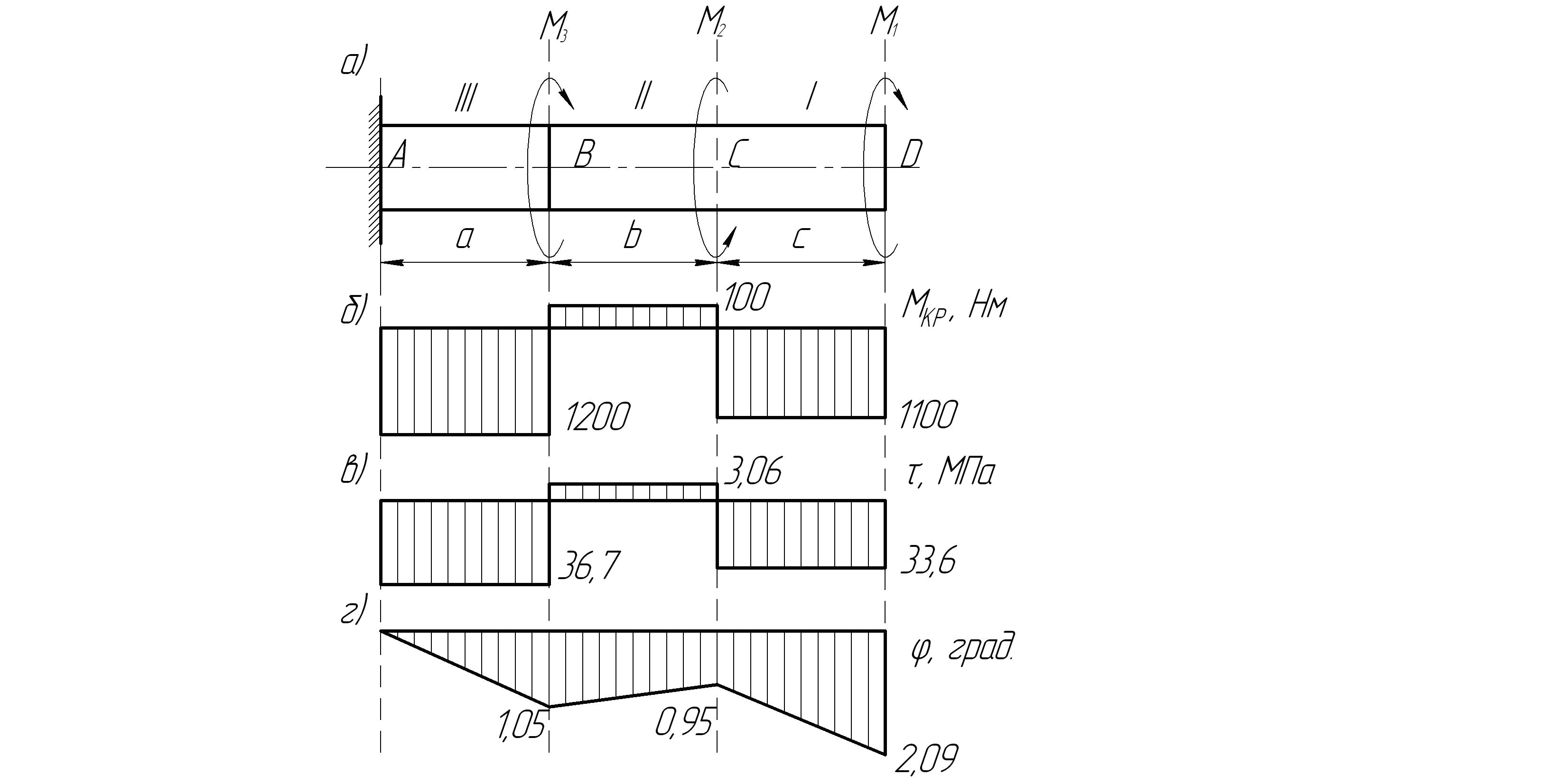
Рис. 7.3. Расчетная схема (а), эпюры крутящих моментов (б), касательных напряжений (в) и углов закручивания (г)
Определяем полярный момент сопротивления поперечного сечения вала:
![]() см3.
см3.
Определяем диаметр
вала на основе формулы
![]() :
:
![]() см.
см.
Принимаем
![]() мм.
мм.
Полярный момент
сопротивления
![]() см3.
см3.
Полярный момент инерции:
![]() см4.
см4.
Строим эпюру максимальных касательных напряжений по длине вала, вычислив напряжения на каждом из трех участков:
![]() Н/см2 = - 33,6
МПа;
Н/см2 = - 33,6
МПа;
![]() Н/см2 = - 3,06
МПа;
Н/см2 = - 3,06
МПа;
![]() Н/см2 = - 36,7
МПа.
Н/см2 = - 36,7
МПа.
Следовательно,
![]() МПа превышает допускаемое напряжение
МПа, но не более чем на 5%, что допустимо.
МПа превышает допускаемое напряжение
МПа, но не более чем на 5%, что допустимо.
Построение эпюры углов закручивания начинаем от заделки вала.
Для сечения А
![]() .
Тогда угол поворота сечения В на участке
III равен:
.
Тогда угол поворота сечения В на участке
III равен:
![]() ,
,
подставив
![]() Н/см2 – модуль сдвига,
- Нм и
- в см, получим:
Н/см2 – модуль сдвига,
- Нм и
- в см, получим:
![]() .
.
Угол поворота сечения С на участке II:
![]() .
.
Угол поворота торца D:
![]() .
.
По полученным значениям строим эпюру углов закручивания по длине вала (см. рис. 7.3, г).
Определяем максимальный относительный угол закручивания вала на III участке, так как на этом участке эпюра имеет наибольшую крутизну:
![]() град/м.
град/м.
Пример 4. Изгиб прямолинейной балки.
Для заданной схемы
нагружения балки (рис. 7.4) построить
эпюры поперечных сил Q,
изгибающих моментов Ми,
определить Ми max
и подобрать балку двутаврового поперечного
сечения при заданном допускаемом
напряжении
![]() МПа.
МПа.
Дано: длины участков
м;
![]() м; сосредоточенная сила
м; сосредоточенная сила
![]() МН; распределенная нагрузка
МН; распределенная нагрузка
![]() МН/м; момент пары сил
МН/м; момент пары сил
![]() МНм.
МНм.
Требуется построить
эпюры
![]() и
и подобрать номер двутавра при допускаемом
напряжении
и
и подобрать номер двутавра при допускаемом
напряжении
![]() МПа.
МПа.
Решение.
1. Определение опорных реакций
Мысленно освобождаем
балку от связей, а их действие заменяем
реакциями
![]() и
и
![]() ,
направленными вертикально вверх (рис.
7.4).
,
направленными вертикально вверх (рис.
7.4).
Составляем два уравнения моментов всех сил относительно точек А и В.

Рис. 7.4. Схема нагружения балки
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Из первого уравнения определяем :
 МН =
МН =
= 23,22 кН.
Из второго уравнения определяем:
 МН
= - 7,22 КН.
МН
= - 7,22 КН.
Проверяем правильность нахождения реакций, составив сумму проекций всех сил на вертикальную ось Y:
![]() ,
,
![]() ,
,
![]() .
.
Следовательно, реакции определены правильно.
2. Построение эпюр изгибающих моментов и поперечных сил
Изображаем схему
балки (рис. 7.5, а), направив реакцию
![]() вниз (так как она получилась отрицательной),
а реакцию
вверх.
вниз (так как она получилась отрицательной),
а реакцию
вверх.
Разбиваем балку на три участка I – III.
Выбираем начало координат в точке А.
а) Строим эпюры и на участке I.
Вводим сечение на
расстоянии Z в пределах
первого участка (![]() ).
).
Определим изгибающий момент в проведенном сечении как алгебраическую сумму моментов от всех внешних сил, приложенных к балке слева от сечения: момент силы берем со знаком плюс, если он направлен по часовой стрелке (стремится изогнуть участок балки вогнутостью вверх).
Вычисляем значения
![]() при:
при:
![]() ,
,
![]() ,
,
![]() м,
м,
![]() кНм,
кНм,
![]() м,
м,
![]() кНм,
кНм,
![]() м,
м,
![]() кНм.
кНм.
Составляем уравнение
для поперечной силы как
![]() :
:
![]() .
.
При построении эпюры достаточно значений , соответствующих границам участка:
,
![]() кН,
кН,
![]() м,
м,
![]() кН.
кН.
б) Строим эпюры и на участке II.
Проводим сечение
в пределах второго участка (![]() ).
).
Составляем уравнения
для
![]() и
и
![]() :
:
![]() ;
;
![]() .
.
Вычисляем значения и при:
м,
![]() кНм,
кНм,
![]() кН;
кН;
![]() м,
м,
![]() кНм;
кНм;
![]() м,
м,
![]() кНм;
кНм;
![]() м,
м,
![]() кНм,
кНм,
![]() кН.
кН.
в) Строим эпюры и на участке III.
Проводим сечение
на расстояние
![]() .
Определяем изгибающий момент в проведенном
сечении от силы Р, действующей на
правую часть балки, применяя при этом
обратное правило знаков:
.
Определяем изгибающий момент в проведенном
сечении от силы Р, действующей на
правую часть балки, применяя при этом
обратное правило знаков:
![]() (знак «-» взят
потому, что момент направлен по часовой
стрелке).
(знак «-» взят
потому, что момент направлен по часовой
стрелке).
Поперечная сила на этом участке:
![]() кН.
кН.
Для построения
эпюры
![]() достаточно двух значений:
достаточно двух значений:
м,
![]() кНм,
кНм,
![]() ,
,
![]() .
.
Построение эпюры и представлены на рис. 7.5.
3. Подбираем номер двутавровой балки.
Максимальный
изгибающий момент на эпюре
![]() (см. рис. 7.5) равен:
(см. рис. 7.5) равен:
![]() кНм.
кНм.
Определяем момент сопротивления поперечного сечения на изгиб:
![]() см3.
см3.
Принимаем двутавр
№12, для которого
![]() см3.
см3.
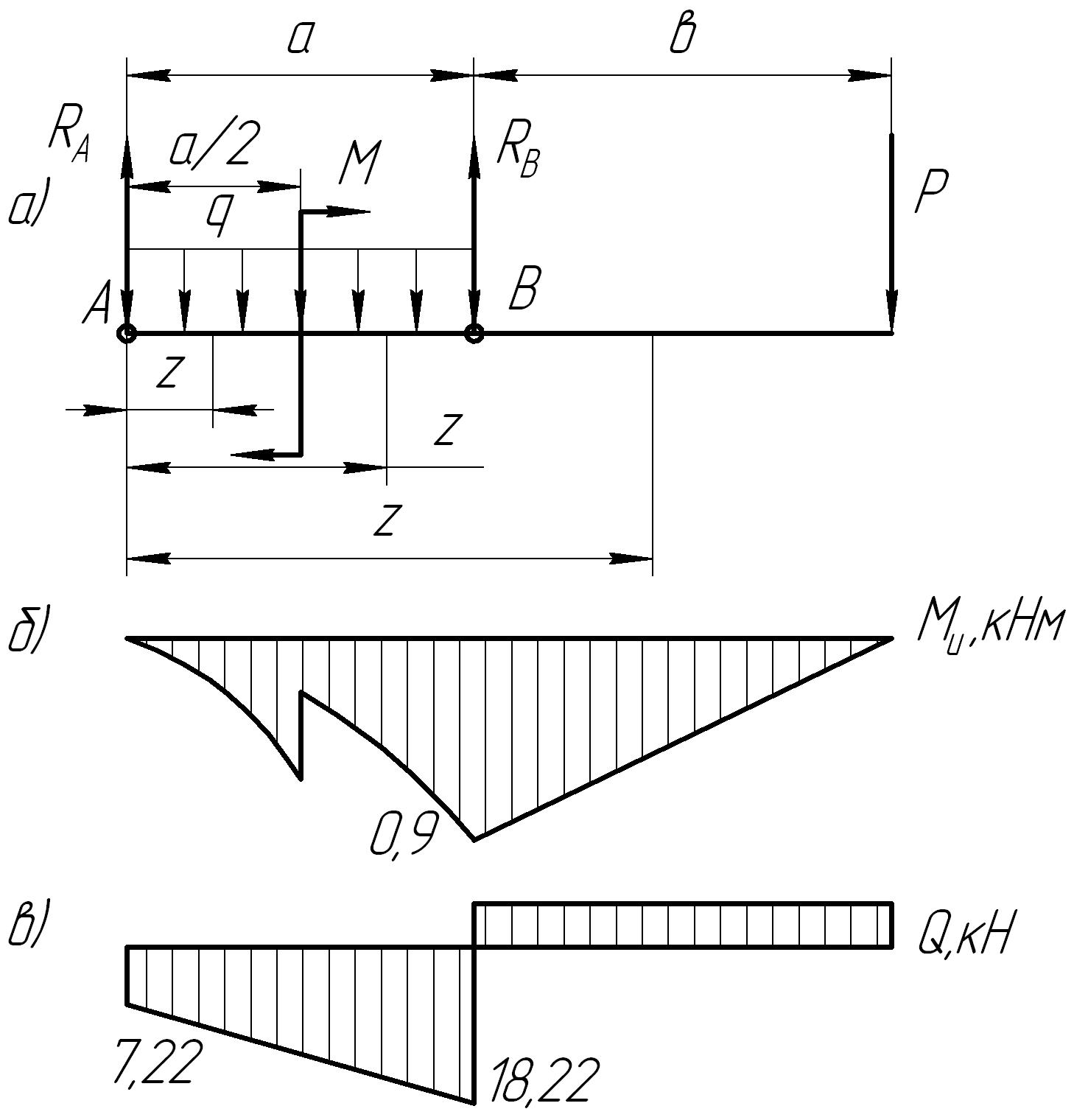
Рис. 7.5. Расчетная схема (а), эпюры изгибающих моментов (б)
и поперечных сил (в)
Пример 5.
Дано: Р = 2ql
1. Составляем расчетную схему. Расчетная схема приведена на рис. 7.8, б.
2. Система имеет
одну неизвестную внешнюю силу – реакцию
![]() .
.
Поскольку эту
реакцию можем определить из уравнения
![]() ,
то система статически определима.
,
то система статически определима.
3. Определяем реакцию опоры :
![]() ,
,
![]() .
.
![]() .
.
4. Перерисуем схему (рис. 7.8, в).
5. Определяем количество участков. Начала и концы распределенных сил совпадают с точками приложения сосредоточенных сил Р, 1,5Р, .
Система имеет два участка (рис. 7.8, в).
6. Составляем аналитические выражения внутренних силовых факторов и строим эпюры.
Участок 1:
![]() .
.
Проведем на
произвольном расстоянии от начала
участка (рис. 8, в), сечение I
– I. Система делится на
две части. С целью определения внутреннего
силового фактора в проведенном сечении
продольной силы
![]() - вправе рассматривать равновесие любой
из полученных частей. Для простоты
вычислений лучше рассмотреть равновесие
той части, где действующих сил меньше.
Рассмотрим равновесие такой части (рис.
7.8, д). В силу вышесказанного продольную
силу
в сечении условно считаем положительной.
- вправе рассматривать равновесие любой
из полученных частей. Для простоты
вычислений лучше рассмотреть равновесие
той части, где действующих сил меньше.
Рассмотрим равновесие такой части (рис.
7.8, д). В силу вышесказанного продольную
силу
в сечении условно считаем положительной.
Составив уравнение равновесия, получаем аналитическое выражение силового фактора
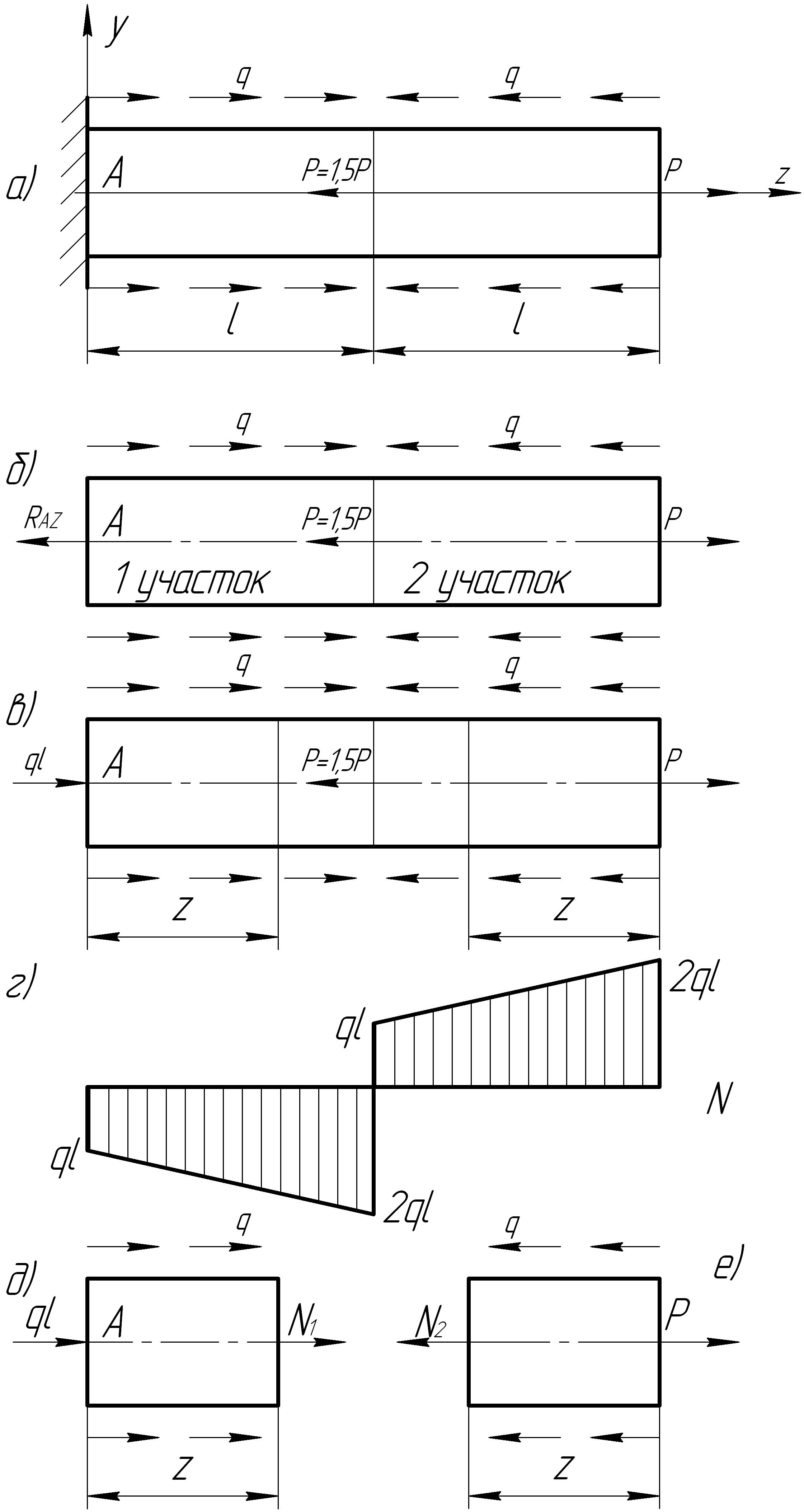
Рис. 7.8
,
![]() ,
,
![]() . (7.1)
. (7.1)
Как видно из формулы
(7.1) продольная сила на I
участке в зависимости от
![]() меняется по прямолинейному закону. Для
построения эпюры
на I участке достаточно
определить значение функции в начале
и конце участка.
меняется по прямолинейному закону. Для
построения эпюры
на I участке достаточно
определить значение функции в начале
и конце участка.
При
![]() ;
;
![]() .
.
При
![]() ;
;
![]() .
.
Отложим найденные значения вдоль ординат от базиса (рис. 8, г), найденные точки соединим прямой. Эпюра обозначается поперечной штриховкой. Знак эпюры указывается на площади эпюры. Поэтому на границах участков указываются абсолютные величины ординат эпюры.
Составим аналитическую зависимость продольной силы на II участке. Для этого опять применим метод сечения (рис. 7.8, в и рис. 7.8, е).
;
![]() ;
;
![]() .
.
![]() .
.
При
![]() ;
;
![]() .
.
При
![]() ;
;
![]() .
.
Строим эпюру продольных сил на II участке.
Решение было правильным если мы стали рассматривать равновесие левой части (рис. 7.9)
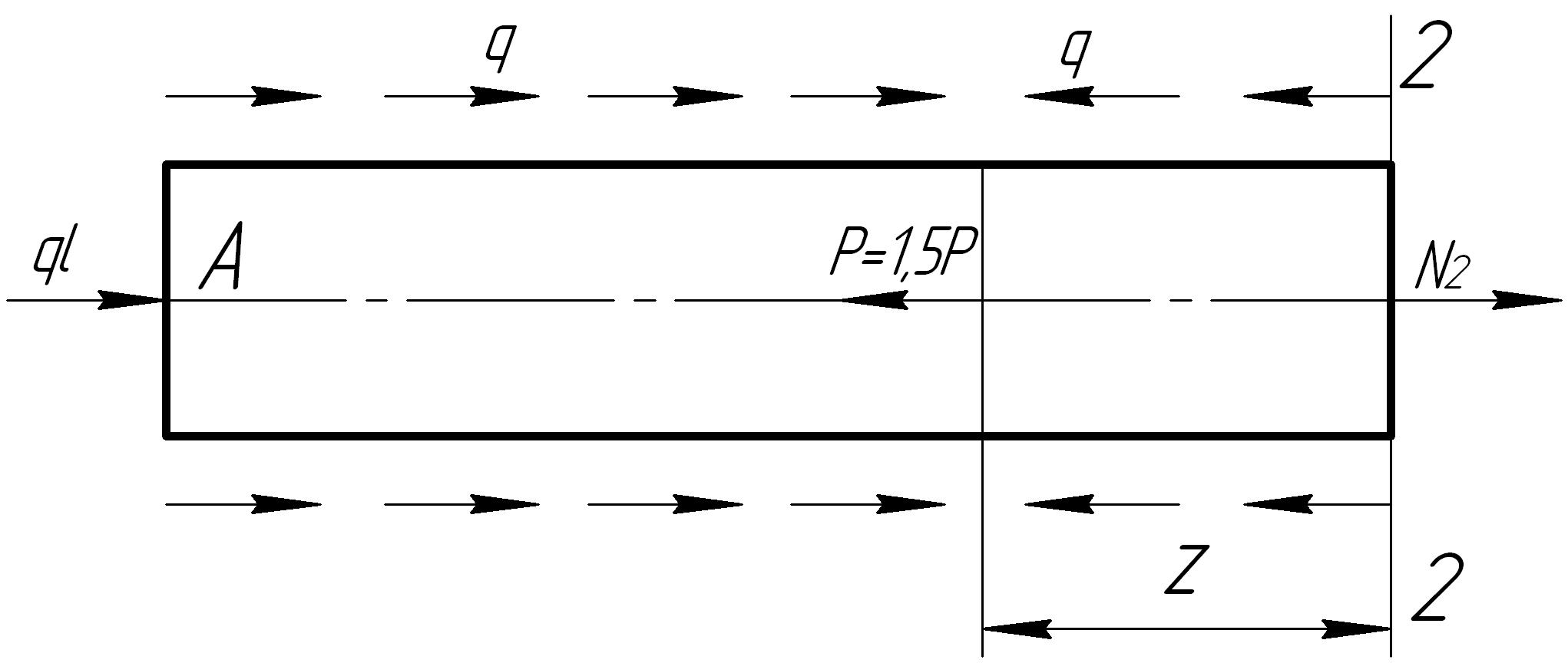
Рис. 7.9. Схема составления аналитического выражения из рассмотрения равновесия левой части бруса
Тогда
;
![]() ;
;
![]() .
.
.
.
При ; .
При ; .
Как видим, получили одни и те же результаты.
Эпюра продольных сил показывает, что брус на I участке сжимается, а на втором растягивается.
6. Проверка правильности построения эпюры (рис. 8, в)
а) на участке с распределенными силами продольные силы меняются по линейному закону;
б) наклон линий соответствует дифференциальной зависимости:
.
в) в местах приложения
сосредоточенных сил
;
![]() ;
имеются скачки, равные по величине
приложенным внешним силам.
;
имеются скачки, равные по величине
приложенным внешним силам.
7. Опасные сечения определяем по местам наибольших значений внутренних силовых фактором. Из эпюры (рис. 7.8, г) видно, что система имеет два равноопасных сечения в точках 1 и 2 (рис. 7.8, а):
В точке 1 максимальная
сжимающая сила
![]() ;
в точке 2 – максимальная растягивающая
сила
.
;
в точке 2 – максимальная растягивающая
сила
.
Однако составление уравнений статики на рассмотрения равновесия рассматриваемой части, как это делали выше (рис. 7.8, д, е) представляет большие неудобства. Поэтому в практике удобнее применять метод сечения с учетом принципа независимости действия сил и продольную силу определять как алгебраическую сумму проекций сил, действующих на рассматриваемую часть, на ось бруса со следующими знаками: если проекция направлена к сечению, то знак «-», если проекция направлена от сечения, то знак «+». Тогда довольно просто можно составить аналитические выражения продольных сил в частности для рассмотренного случая:
![]() ;
;
![]() или
или
![]() (если
определяется из левой части).
(если
определяется из левой части).
Как видим, отношения получились такими же.
ПРИМЕР 6.
Кручением называется
один из видов простого нагружения, когда
в поперечном сечении бруса имеется
только один внутренний силовой фактор
– крутящий момент
.
Сразу же отметим, что такое нагружение
наблюдается только в том случае, когда
внешние силы дают момент только
относительно оси бруса
![]() .
Брус, подвергаемый скручиванию, называется
валом. Построение эпюры
проанализируем на конкретном примере
(рис. 7.10), где
.
Брус, подвергаемый скручиванию, называется
валом. Построение эпюры
проанализируем на конкретном примере
(рис. 7.10), где
![]() .
.

Рис. 7.10. Схема построения эпюры крутящих моментов
1. Составляем
расчетную схему. Для этого заделку
заменяем ее реакцией
![]() (рис. 7.10, б).
(рис. 7.10, б).
2. Из рис. 7.10, б
видно, что система статически определима.
Неизвестный момент заделки (
)
определяем из уравнения равновесия
![]() .
.
![]() ;
;
![]() .
.
3. Определяем количество участков. Данная система имеет 4 участка.
4. Составляем аналитические выражения и строим эпюры внутреннего силового фактора по участкам. Заметим, что можно определить из рисунков схем равновесия частей бура. Однако это составляет определенные неудобства, проще составить аналитическое выражение , используя непосредственно принцип независимости действия сил с учетом равновесия рассматриваемой части. При этом только учитывать знаки от внешних следующим образом, если смотреть на сечение со стороны внешней нормали к нему, то внешние моменты, направленные против часовой стрелки, дают со знаком «-», а моменты, направленные по часовой стрелке, дают со знаком «+». Используя эту схему знаков, сразу же составляем:
![]() от
не зависит, следовательно, на этих
участках имеет постоянное значение.
от
не зависит, следовательно, на этих
участках имеет постоянное значение.
![]() ;
;
![]() ,
при
,
при
![]() ;
;
![]() ;
;
при
![]() ;
;
![]() .
.
![]() ;
;
![]() .
.
При
![]() ,
,
![]() ;
;
При
![]() ;
;
![]() .
.
Эпюра крутящих моментов представлена на рис. 7.10, б. Штриховка эпюры крутящего момента показана на рис. 7.10, б.
Эпюра получилась бы точно такая же, если мы задачу решили исходя из правого конца, или же часть задачи решили исходя из левого, а другую часть – из правого конца.
5. После решения задачи можно проверить правильность построения эпюры. Как видим, все правила проверки выполняются: там, где есть сосредоточенные моменты имеются на эпюре скачки, равные величине приложенного сосредоточенного момента: там, где имеются распределенные моменты (участки 3 и 4), там эпюра изменяется по линейному закону и выполняется условие дифференциальной зависимости:
![]()
![]() .
.
6. Определение
опасного сечения. Опасное расчетное
сечение определяется из эпюры по
максимальному действительному значению
.
На данной схеме имеются два равноопасных
сечения 1 и 2 и первый участка (где все
сечения равноопасны) с максимальным
значением крутящего момента
![]() .
.
ПРИМЕР 7.
Изгибом называется вид нагружения, когда в поперечном сечении возникает только изгибающий момент (случай чистого изгиба) или только изгибающий момент и поперечная сила (случай поперечного изгиба). Здесь не будут рассмотрены случаи так называемого продольно-поперечного изгиба, хотя при достаточно прочном овладении методом сечения, построение эпюр в этом и других видах нагружения не представляет особых трудностей.
Мы разберем
построение эпюр при чистом и поперечном
изгибе в случаях, когда плоскость
действия внешнего силового фактора
лежит в одной из главных плоскостей
бруса (главные плоскости
![]() и
и
![]() ).
Такой вид изгиба называется плоским
(прямым). При плоском изгибе изогнутая
ось бруса все время лежит в той же главной
плоскости, в которой находится плоскость
действия внешнего силового фактора.
).
Такой вид изгиба называется плоским
(прямым). При плоском изгибе изогнутая
ось бруса все время лежит в той же главной
плоскости, в которой находится плоскость
действия внешнего силового фактора.
Брусья, испытывающие изгиб, называются балками. В зависимости от вида опор балки могут быть консольно-защемленными, двухопорными, многоопорными с консолями и без них (рис. 7.11) и т.д.
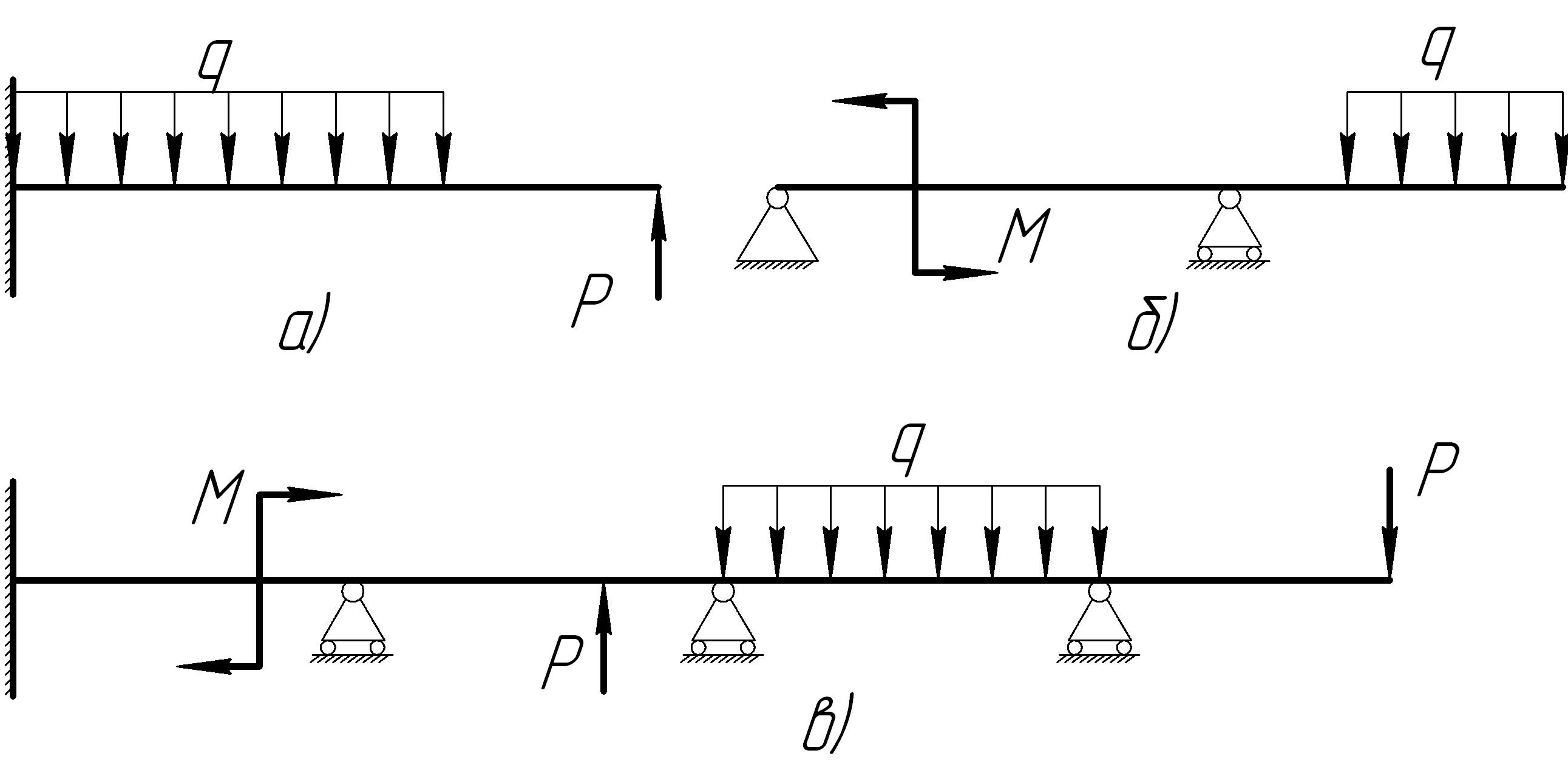
Рис. 7.11. Виды балок:
а) консольно-защемленная балка;
б) двухопорная балка с консолью;
в) многоопорная балка с консолью.
Построение эпюр изгибающих моментов (М) и поперечных сил рассмотрим на конкретном примере (рис. 7.12).
1. Выбираем расчетную схему. Для этого заменяем реакциями (рис. 7.12, б).
2. Из расчетной схемы видно, что система статически определима.
3. Определяем
реакции опор
![]() и
и
![]() :
:
![]() ;
;
![]() .
.
![]() .
.
![]() ;
;
![]() .
.
![]() .
.
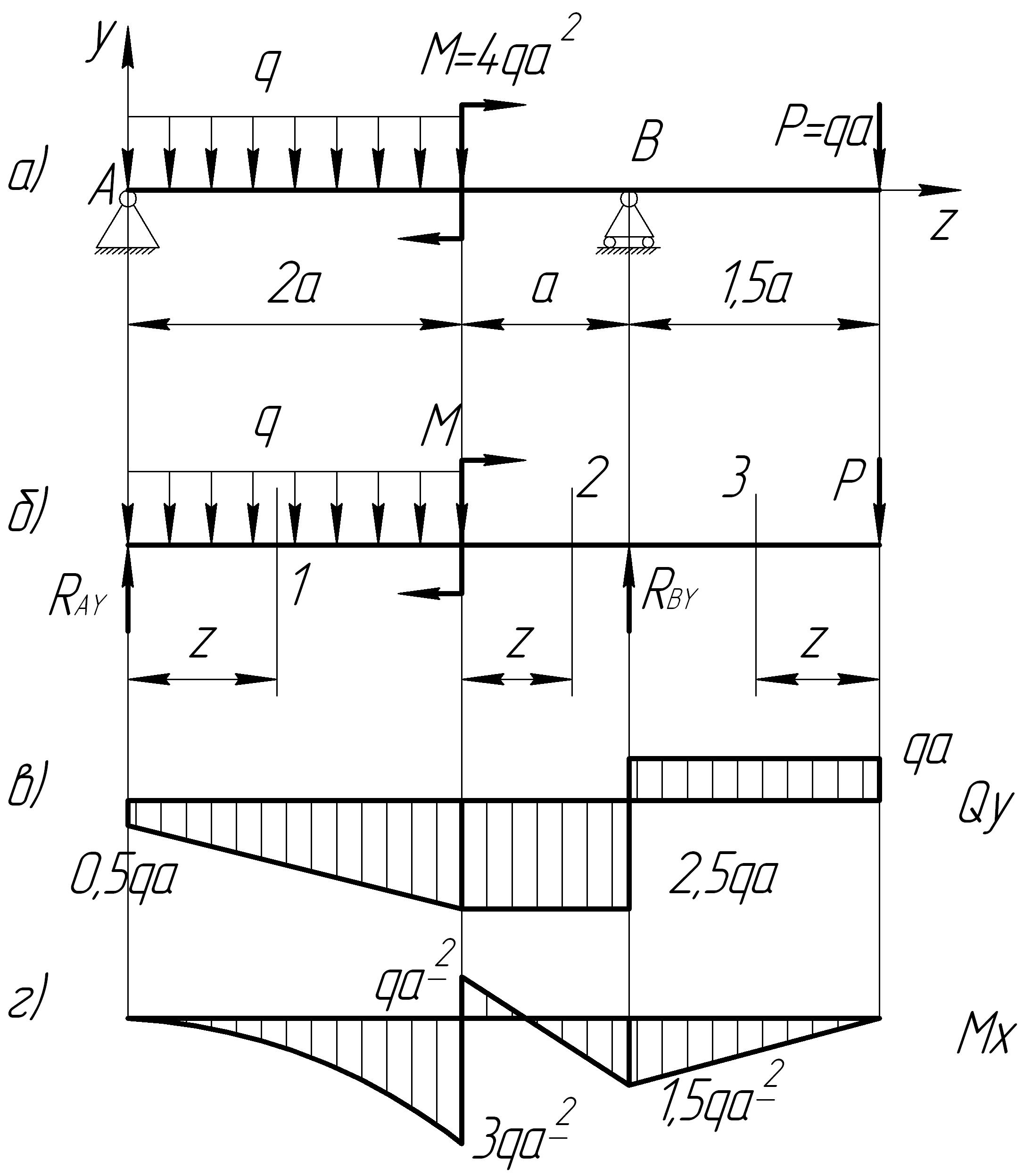
Рис. 7.12. Схема построения эпюр при изгибе
Проверка:
![]() ;
;
![]() ;
;
![]() .
.
Реакцию опоры
получили с отрицательным знаком. Это
говорит о том, что на самом деле реакция
опоры направлена вниз. Для решения
задачи можно оставить принятое направление
,
но при этом при вычислении внутренних
силовых факторов вместо
ставить
![]() ;
можно изменить на расчетной схеме
направление реакции
вниз в формулах для вычисления внутренних
силовых факторов вместо
ставить
;
можно изменить на расчетной схеме
направление реакции
вниз в формулах для вычисления внутренних
силовых факторов вместо
ставить
![]() .
Результат решения от этого не изменится.
.
Результат решения от этого не изменится.
4. Определяем количество участков. Наша система имеет три участка (рис. 7.11, б).
5. Составляем аналитические выражения и строим эпюру внутренних силовых факторов по участкам. При составлении аналитических выражений применяем метод сечения. При этом можно строить схемы равновесия рассматриваемой части и оттуда определять внутренние силовые факторы. Практически проще составлять аналитические выражения, применяя принцип независимости действия сил и следующие схемы (рис. 7.13). Эти схемы получаются из схем равновесия рассматриваемой части и показанные направления внешних сил дают ранее принятые знаки внутренних силовых факторов.
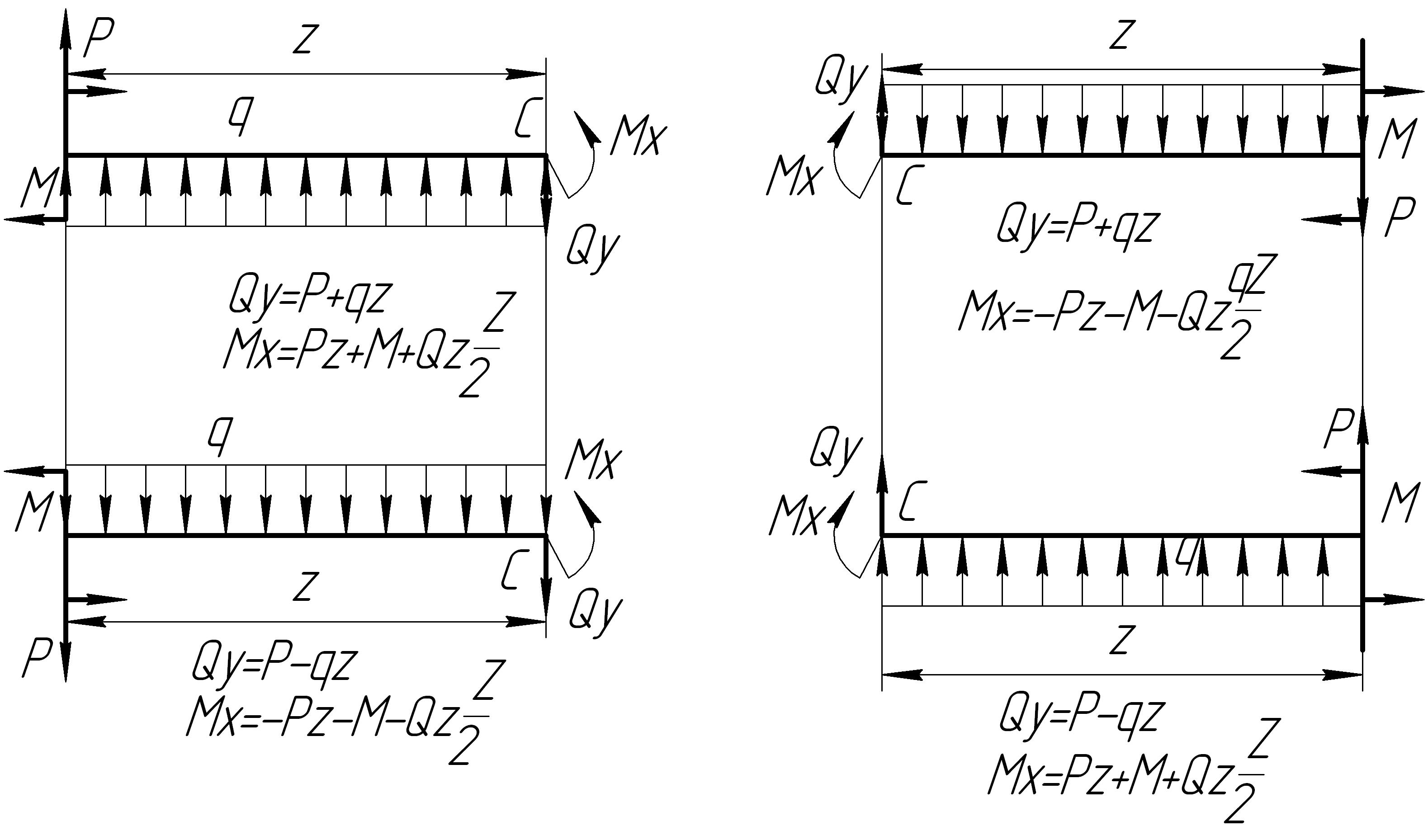
Рис. 7.13. Схема знаков внутренних силовых факторов в зависимости от направления действия внешних сил (С - сечение)
а) при рассмотрении равновесия левой от сечения части бруса;
б) при рассмотрении равновесия правой от сечения части бруса
Участок 1:
![]() .
.
Проведем на
расстояние
![]() от начала участка сечение 1 – 1 (рис.
7.12, б). Используя схему знаков (на рис.
7.13), составляем аналитическое выражение
от начала участка сечение 1 – 1 (рис.
7.12, б). Используя схему знаков (на рис.
7.13), составляем аналитическое выражение
![]() и
и
![]() :
:
![]() ;
при
;
при
![]() ,
,
![]() ;
;
при
![]() ,
,
![]() .
.
![]() ;
при
,
;
при
,
![]() ;
;
при
,
![]() .
.
Поскольку изменяется в зависимости от по прямолинейному закону, то для построения эпюры достаточны значения поперечной силы в двух точках (на границах участка). А изменяется в зависимости от по кривой второго порядка (квадратичная парабола). Поэтому для построения эпюры требуются значения его на границах участка и по крайней мере в одной из точек на участке. Если эпюра изгибающего момента на участке не изменяется по кривой с максимумом или минимумом, то для построения кривой за третью точку берут любую точку участка (обычно середину участка). В данном случае эпюра поперечных сил на участке не пересекает базисную линию. Если эпюра поперечных сил пересекает базисную линию, то в точке пересечения эпюра изгибающих моментов имеет максимум или минимум (см. правила проверки правильности построения эпюр). В этих случаях за третью точку берется координата точки пересечения, которую можно определить из условия равенства нулю аналитического выражения поперечной силы на участке. В этом смысле построение эпюры поперечной силы должно предшествовать построению эпюр изгибающих моментов.
В нашем случае
эпюра поперечных сил на этом участке
не пересекает базисную линию (рис. 7.12,
в). Поэтому для построения эпюры на этом
участке определим его значение при
![]() .
.
При
,
![]() .
.
По полученным
значениям 0;
![]() ;
;
![]() построим параболу (эпюру изгибающего
момента) (рис. 7.12, г).
построим параболу (эпюру изгибающего
момента) (рис. 7.12, г).
Участок 2:
![]() .
.
Проведем сечение
![]() на расстояние
на расстояние
![]() от начала участка (рис. 7.12, б).
от начала участка (рис. 7.12, б).
![]() .
.
На этом участке имеет постоянное значение и от координаты не зависит.
![]() .
.
При
![]() ,
,
![]() .
.
При
![]() ,
,
![]() .
.
Эпюры на втором участке представлена на рис. 7.12, в и на рис. 7.12, г.
Участок 3:
![]() .
.
Для облегчения
решения рассмотрим правую часть. Для
этого участка проведем сечение на
расстоянии
![]() от начала участка, помещенного в конце
консоли (рис. 7.12, б).
от начала участка, помещенного в конце
консоли (рис. 7.12, б).
Используя правило
знаков (рис. 7.12, б), составим аналитические
выражения
![]() и
и
![]() .
.
![]() .
имеет постоянное значение и от координаты
не зависит.
.
имеет постоянное значение и от координаты
не зависит.
![]() ;
;
при
![]() ;
;
![]() ;
;
при
![]() ;
;
![]() .
.
Эпюры и представлены на рис. 7.12, в и рис. 7.12, г.
ПРИМЕР 8.
Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рис. 7.14.
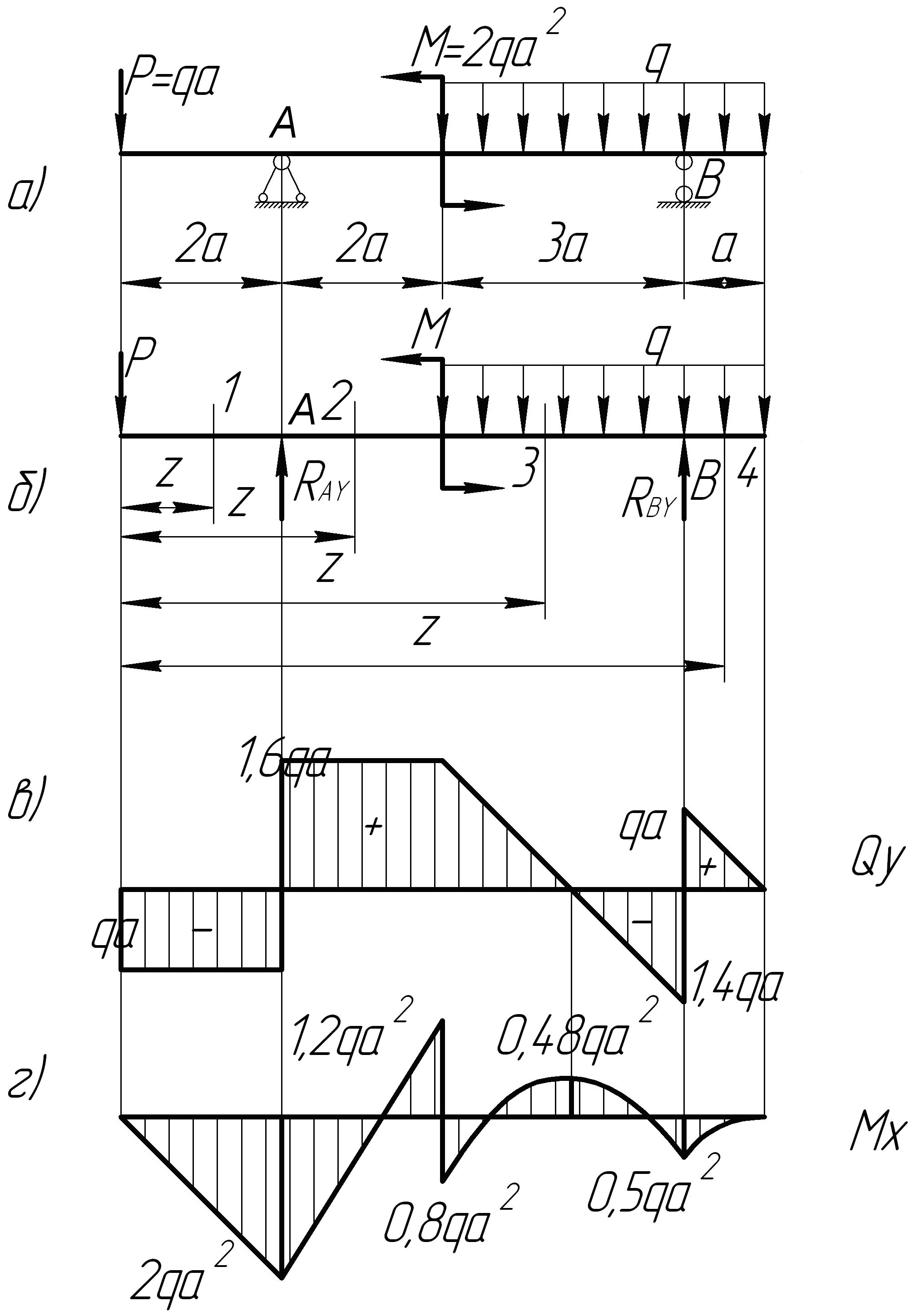
Рис. 7.14. Схема построения эпюр поперечной силы и
изгибающего момента
1. Расчетная схема (рис. 7.14, б) показывает, что на балку кроме заданных (известных) сил, действуют две реакции (неизвестных сил).
2. Определяем реакции опор, составляя уравнения моментов относительно точек опора А и В.
,
![]() .
.
Отсюда
![]() .
.
,
![]() .
.
Отсюда
![]() .
.
Производим проверку ;
![]() .
.
Опорные реакции
и
![]() определены правильно.
определены правильно.
3. Заданная балка имеет четыре участка (рис. 7.14, б).
4. Составляем аналитические выражения и строим эпюры внутренних силовых факторов по участкам.
Если рассмотреть поперечные сечения, то в них будут в наличии только и . Остальные внутренние силовые факторы равны нулю.
Участок 1:
![]() .
.
![]() ;
;
![]() .
.
![]() ;
при
;
;
при
;
![]() ;
при
;
при
![]() ;
;
![]() .
.
Участок 2:
![]() .
.
![]() ;
;
![]() .
.
![]() ,
при
,
при
![]() ;
;
![]() ;
;
при
![]() ;
;
![]() .
.
Участок 3:
![]() .
.
![]() ,
меняется по линейному закону.
,
меняется по линейному закону.
При
,
![]() ;
;
при
![]() ,
,
![]() .
.
![]() .
.
меняется в зависимости от по кривой второго порядка (квадратичная парабола). Находим сначала на границах участка.
При
,
![]() ;
;
при
,
![]() .
.
Для построения
параболы необходимо определить значение
хотя бы еще в одной точке. Для выбора
третьей точки используем эпюру
.
Из эпюры видно, что при
![]() (рис. 7.14, в)
(рис. 7.14, в)
![]() .
.
Отсюда определим
![]() :
:
![]() ;
;
![]() .
.
Определим теперь
значение
:
при
![]() .
.
![]() .
.
Согласно правил проверки правильности построения эпюр при на третьем участке должен иметь максимум.
При
![]() ,
,
![]() .
.
По полученным значениям строим эпюру изгибающего момента на третьем участке.
Участок 4:
![]()
![]() ;
;
![]() меняется по линейному закону:
меняется по линейному закону:
При
,
![]() ;
;
при
![]() ,
,
![]() .
.
![]()
На четвертом
участке график
![]() меняется по параболическому закону.
Сперва находим значение
на концах участка.
меняется по параболическому закону.
Сперва находим значение
на концах участка.
При
,
![]() ;
;
При
,
![]() .
.
Определяем значение
в любой третьей точке. График эпюры
не пересекает базисную линию, поэтому
третье значение
определяем, допустим, при
![]() .
.
При ,
![]() .
.
Необходимо отметить, что здесь решение задачи приведено рассмотрением участков последовательно, начиная с левого конца балки. Результат не изменился бы, если решение задачи полностью производили, начиная с правого конца, или же часть задачи решили с левого, а часть – с правого конца.
5. Применяя правило
правильности построения эпюр внутренних
силовых факторов, убеждаемся в правильности
построения эпюр. В частности, на эпюре
поперечных сил в местах приложения
сосредоточенных сил имеются скачки,
равные приложенным силам:
![]() ;
;
.
;
;
.
На участках с
распределенной силой поперечная сила
меняется по линейному закону. На эпюре
изгибающих моментов в месте приложения
сосредоточенного момента имеется скачок
равный
![]() .
Применив дифференциальные зависимости,
также можно убедиться в согласованности
величин и законов поперечных сил с ходом
графика изгибающего момента. Например,
на третьем участке поперечная сила
меняется по прямолинейному закону, при
этом при движении
слева направо (т.е. положительное
направление оси
)
знак поперечной силы меняется с плюс
на минус. При этом на эпюре изгибающих
моментов график должен иметь максимум
при
.
Действительно, там, где поперечная сила
равна нулю, на эпюре изгибающих моментов
достигается максимум.
.
Применив дифференциальные зависимости,
также можно убедиться в согласованности
величин и законов поперечных сил с ходом
графика изгибающего момента. Например,
на третьем участке поперечная сила
меняется по прямолинейному закону, при
этом при движении
слева направо (т.е. положительное
направление оси
)
знак поперечной силы меняется с плюс
на минус. При этом на эпюре изгибающих
моментов график должен иметь максимум
при
.
Действительно, там, где поперечная сила
равна нулю, на эпюре изгибающих моментов
достигается максимум.
6. Выбор опасного
сечения. При изгибе опасное сечение
выбирается по эпюре изгибающих моментов.
В нашем примере опасным сечением является
сечение на опоре А, где
![]() .
.
ПРИМЕР 9.
Рамами называются стержневые конструкции, где стержни жестко связаны между собой. Если все оси стержней рамы и внешние силы, действующие на раму, лежат в одной плоскости, то рама называется плоской. Как уже было отмечено выше, для плоских систем, в частности и для плоских рам, используя уравнения статики можно определить только три реакции опор. Если реакций опор больше чем три, то рамы получаются статически неопределимыми, такие рамы мы здесь не будем рассматривать. Принципиально, построение эпюр внутренних силовых факторов в рамах не отличаются от построения эпюр в вышеприведенных системах. Применяется метод сечения. Однако имеются некоторые особенности. Так, например, в углах (узлах) рамы сходятся стержни с разными направлениями, поэтому в рамах узлы также являются границами участков. Для определения поперечных и продольных сил применяются правила статики в несколько обобщенном виде: для определения поперечной силы все внешние силы, действующие на рассматриваемую часть, проектируются на плоскость сечения, а для определения продольной силы – проектируются на ось (направления) стержня. Знаки остаются такими же, но эпюры относительно базиса не всегда удается расположить согласно знакам, по этой причине эпюре располагаются несколько произвольно, но с обязательным указанием знаков на эпюрах.
При определении изгибающих моментов знак изгибающего момента может применяться не так строго, как при изгибе, но обязательно учитываются сжимаемые слои. Эпюра изгибающих моментов строится на сжатых волокнах.
Конкретно особенности построения эпюр в плоских рамах разберем на примере (рис. 7.15).

Рис. 7.15. Расчетная схема рамы
Рама статически
определимая, т.е. реакции опор
![]() ,
,
можно определить из условий равновесия.
,
,
можно определить из условий равновесия.
,
![]() ;
;
 ;
;
![]() .
.
,
![]() ;
;
![]() ;
;
![]() .
.
![]() ,
,
![]() ;
;
![]() ;
;
![]() .
.
Проверка:
,
![]() ;
;
![]() ;
;
![]() .
.
Реакции опор
,
и
![]() определены правильно.
определены правильно.
Рама имеет пять участков (рис. 7.15). По участкам строим эпюры внутренних силовых факторов. Для построения эпюр внутренних силовых факторов (продольной силы N, поперечной силы Q и изгибающего момента Мизг) вынесем ось рамы (рис. 7.16).

Рис. 7.16. Эпюры внутренних силовых факторов
Участок 1:
![]() .
.
![]() (сжатие).
(сжатие).
![]() .
.
![]() ;
при
,
;
при
,
![]() ;
при
;
при
![]() ,
,
![]() .
.
Участок 2:
![]() .
.
![]() (сжатие).
(сжатие).
![]() .
.
![]() меняется по
линейному закону;
меняется по
линейному закону;
при
,
![]() ;
при
;
при
![]() ,
,
![]() .
.
Участок 3:
![]() .
.
![]() (продольной силы
нет).
(продольной силы
нет).
![]() .
.
![]() меняется по
линейному закону;
меняется по
линейному закону;
при
,
![]() ;
;
при
![]() ,
,
![]() .
.
4 и 5 участки проще рассматривать, начиная с опоры В.
Участок 4:
![]() .
.
![]() (растяжение).
(растяжение).
![]() .
.
![]() .
.
![]() от
от
![]() не зависит,
не зависит,
![]() .
.
Участок 5:
![]() .
.
![]() .
.
![]() ;
;
при
![]() ,
,
![]() ;
;
при
![]() ,
,
![]() .
.
![]() меняется по
параболическому закону. Найдем значения
меняется по
параболическому закону. Найдем значения
![]() на границах участка.
на границах участка.
При
,
![]() ;
при
,
;
при
,
![]() .
.
Находим третью точку. График эпюры поперечных сил пересекает базисную линию, причем при движении слева направо изменяет знак с плюса на минус. Поэтому там, где поперечная сила равна нулю, на эпюре Мизг должен достигаться максимум. Координату максимума находим из условия
![]() ;
;
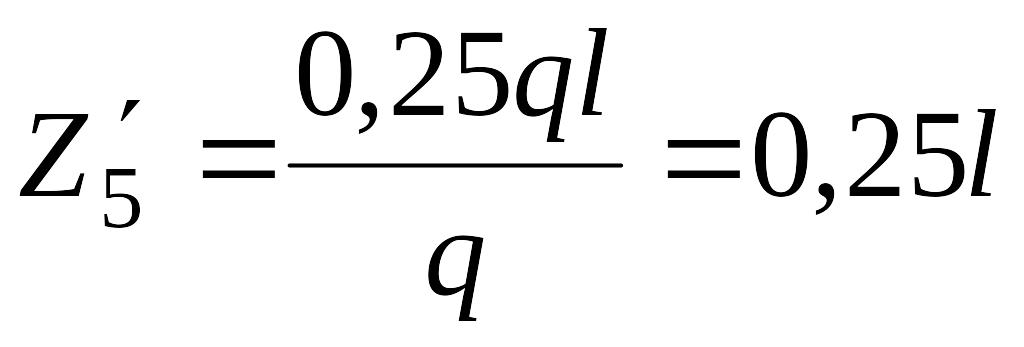 .
.
Найденное значение
![]() подставим в аналитическое выражение
.
подставим в аналитическое выражение
.
При
![]() ;
;

Для проверки правильности построения эпюр применяются те же правила, что и при изгибе балок. При проверке эпюр в рамах необходимо обратить внимание на величины моментов в узлах рамы: если нет приложенного сосредоточенного момента, то величины моментов на сходящихся стержнях равны и сжимают одинаковые волокна (узлы Д, Е, рис. 7.16, е), если в узле приложен сосредоточенный момент, то на сходящихся стержнях в эпюре моментов должен быть скачок, равный величине приложенного момента (узел С, рис. 7.16, в). Это наглядно видно, если мысленно расположить сходящиеся стержни на одной линии.
В рамах, также как и в балках, опасное сечение В определятся по эпюре изгибающих моментов.
ПРИМЕР 10.
Построение эпюр в кривых брусьях принципиально не отличается от построения эпюр в рамах и балках. Однако, вследствие особенностей кривого бурса имеются некоторые особенности в составлении аналитических выражений внутренних силовых факторов. Рассмотрим плоский кривой брус, т.е. такой брус у которого изогнутая ось и действующие силы лежат в одной плоскости, притом ось изогнута под определенным, постоянным радиусом (рис. 7.17).
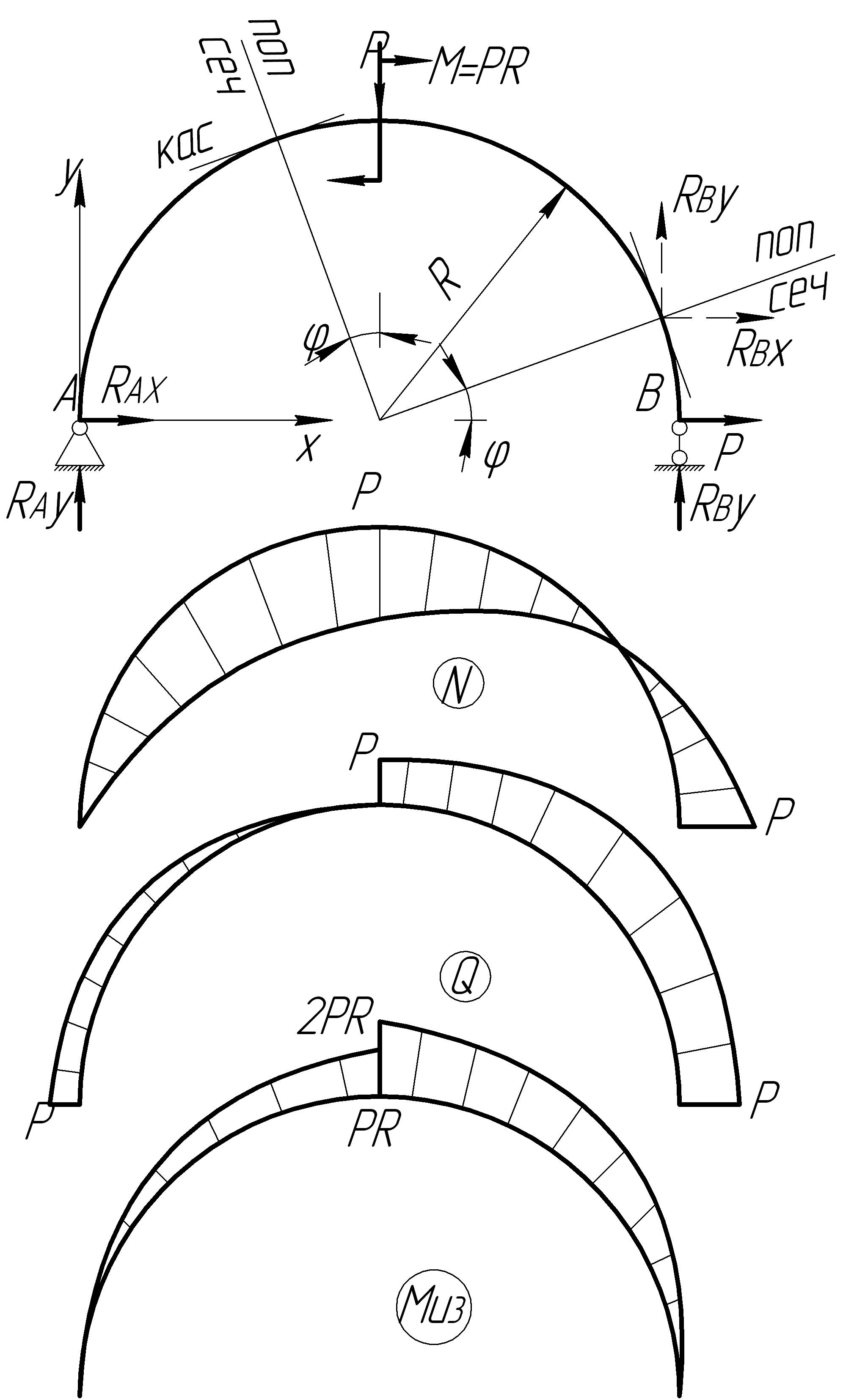
Рис. 7.17. Построение эпюр внутренних силовых факторов
и кривых брусьях:
б) эпюра N;
в) эпюра Q;
г) эпюра М
В кривом брусе аналитические выражения внутренних силовых факторов составляются в виде функции от угла поворота радиуса кривизны оси бруса, поскольку поперечное сечение является радиальным сечением.
Система статически определимая. Определяем реакции опор.
,
![]() ;
;
![]() .
.
;
,
![]() .
.
;
![]() ,
,
![]() .
.
Проверка:
,
![]() .
.
Система имеет два участка (рис. 7.17, а). Строим эпюры по участкам.
Первый участок:
![]() (рис. 7.17, а).
(рис. 7.17, а).
![]() .
.
При
![]() ,
,
![]() ;
при
;
при
![]() ,
,
![]() .
.
Находим третью точку.
При
![]() ,
,
![]() .
.
![]() .
.
При
,
![]() ;
;
при
,
![]() ;
;
при
![]() ,
,
![]() .
.
Составим аналитическое выражение изгибающего момента. Знак изгибающего момента принимается следующим образом: если внешняя сила увеличивает кривизну (уменьшает радиус) бруса, то изгибающий момент положительный; если внешняя сила уменьшает кривизну (увеличивает радиус), то изгибающий момент отрицательный. Эпюра изгибающего момента строится на сжатых волокнах
![]() ;
;
при
,
;
при
,
![]() ;
при
,
;
при
,
![]() .
.
Второй участок: (рис. 17, а).
Для удобства схема действующих сил показана в проведенном сечении.
![]()
При
,
![]() ;
при
,
;
при
,
![]() .
.
![]() .
.
При
,
![]() ;
при
,
;
при
,
![]() .
.
![]()
При
,
![]() ;
при
,
;
при
,
![]() .
.
Построенные эпюры внутренних силовых факторов N, Q и Мизг представлены на рис. 7.17 б, в, г.
Для проверки правильности построения эпюр применяются те же правила. На эпюрах поперечных и продольных сил имеются скачки там, где приложена соответствующая сосредоточенная сила, а на эпюре изгибающего момента имеется скачок в месте приложенного сосредоточенного момента. Величины скачков соответственно равны приложенным внешним силам.
В кривых стержня опасное сечение преимущественно определяется по эпюре изгибающих моментов. Кривые стержни могут входить в рамы как элемент, при этом на прямолинейных стержнях (участках) эпюры строится также, как в выше разобранной раме, а на криволинейных участках как в криволинейных брусьях.
ПРИМЕР 11.
Стержень с пространственно-ломаной осью – это по существу плоская, пространственная или плоско-пространственная рама, имеющая только одну опору – жесткую заделку (жесткое замещение). Притом плоский стержень с ломаной осью этой такой, у которого все оси стержней расположены в одной плоскости, и к тому же все действующие на стержень силы расположены в этой же плоскости. При этом максимальное количество внутренних силовых факторов три: продольная сила N, поперечная сила Q и изгибающий момент Мизг. Сразу отметим, что индексы при Q и М будут зависеть от конкретной схемы подвижной системы координат.
Стержень будет представлять плоско-пространственную раму, если у него оси всех стержней лежат в одной плоскости, а действующие на него силы будут лежать в плоскости, перпендикулярной к плоскости ломаного стержня. В этом случае в стержне могут быть в наличии все шесть внутренних силовых факторов.
А стержень с ломаной осью, у которого оси стержней не лежат в одной плоскости, представляет собой пространственную раму. В этом случае не только в системе, но и в одном сечении могут быть в наличии все шесть внутренних силовых факторов.
Если студент хорошо освоил построение эпюр внутренних силовых факторов в вышерассмотренных случаях, то построение эпюр внутренних силовых факторов в стержнях с ломаной осью не представляет особой трудности. Однако надо обратить внимание на некоторую специфику при построении эпюр. Обычно при построении эпюр рассмотрение участков начинают со свободного конца. Индексы при внутренних силовых факторах , , , определяют относительно подвижной системы координат. Систему координат предпочтительно выбирают правую. За положительное направление оси Z выбирают направление от сечения. При этом знаки поперечных сил и изгибающих моментов определяются рассмотрением действующей на рассматриваемую часть системы сил с положительного направления осей X и Y.
Рассмотрим конкретный пример (рис. 7.18).
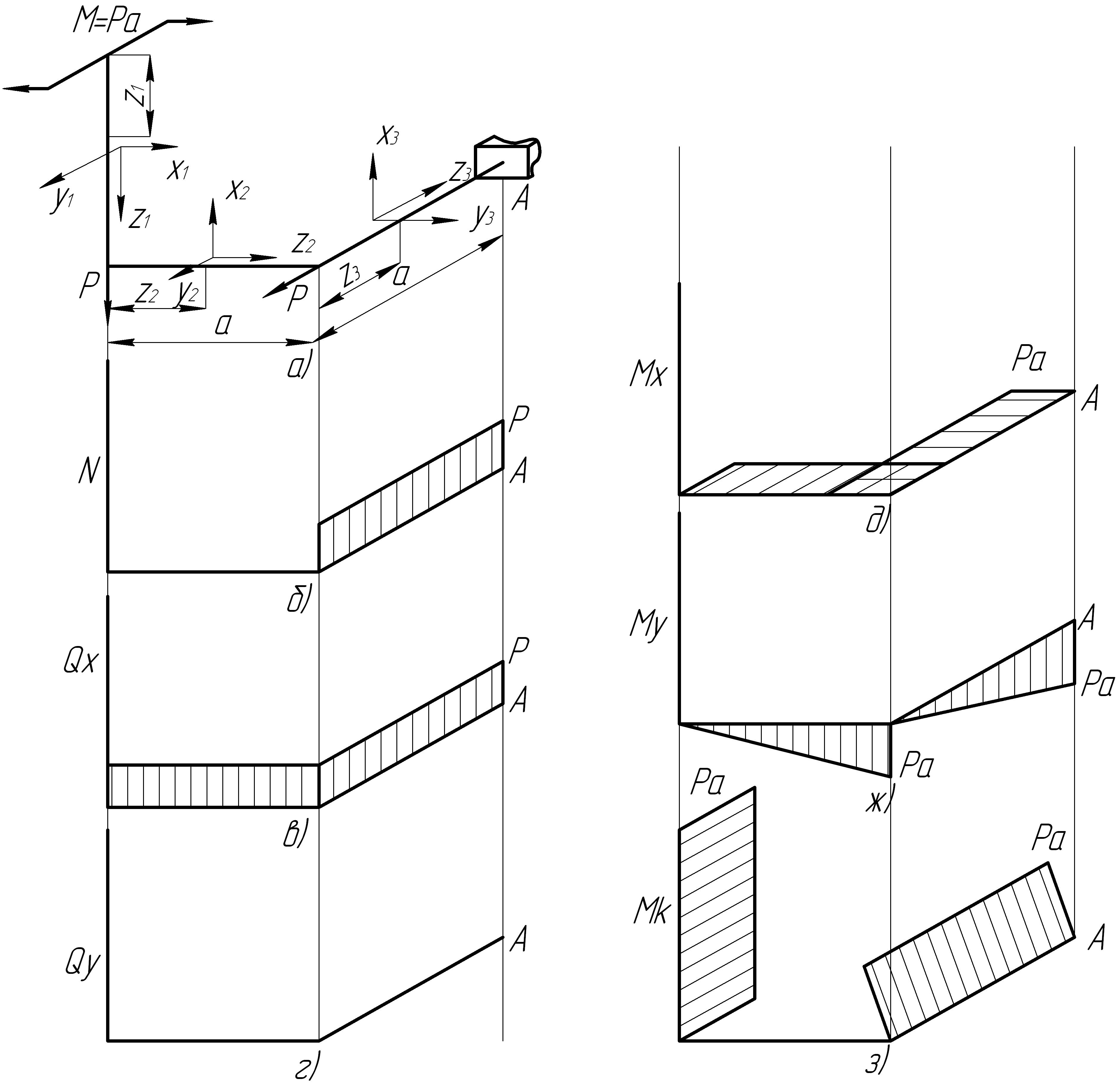
Рис. 7.18. Построение эпюр внутренних силовых факторов в
стержне с ломаной осью
Мысленно построим на данных стержнях, как на ребрах, геометрическую фигуру (мы рассматриваем только такие стержни, в которых оси участков, совпадают с направлениями прямоугольной системы координат, поэтому геометрической фигурой будет куб или параллелепипед). Такое построение облегчает построение эпюры внутренних силовых факторов.
Выбираем подвижную систему координат и сразу обозначим схему расположения осей на участках (рис. 7.18).
Система имеет три участка. Как видно из рисунка, система пространственная. Строим эпюры внутренних силовых факторов по участкам.
Участок 1:
![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Участок 2:
![]() .
.
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
при
,
![]() ;
при
,
;
при
,
![]() .
.
![]() .
.
Участок 3:
![]() .
.
![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
при
,
![]() ;
при
;
при
![]() ,
,
![]() ;
;
![]() .
.
Построенные эпюры внутренних силовых факторов приведены на рис. 7.18 б, в, г, д, ж, з.
Однако для удобства анализа предпочтительнее эпюры сил совместить на одном рисунке, а эпюры моментов на втором рисунке (рис. 7.19).
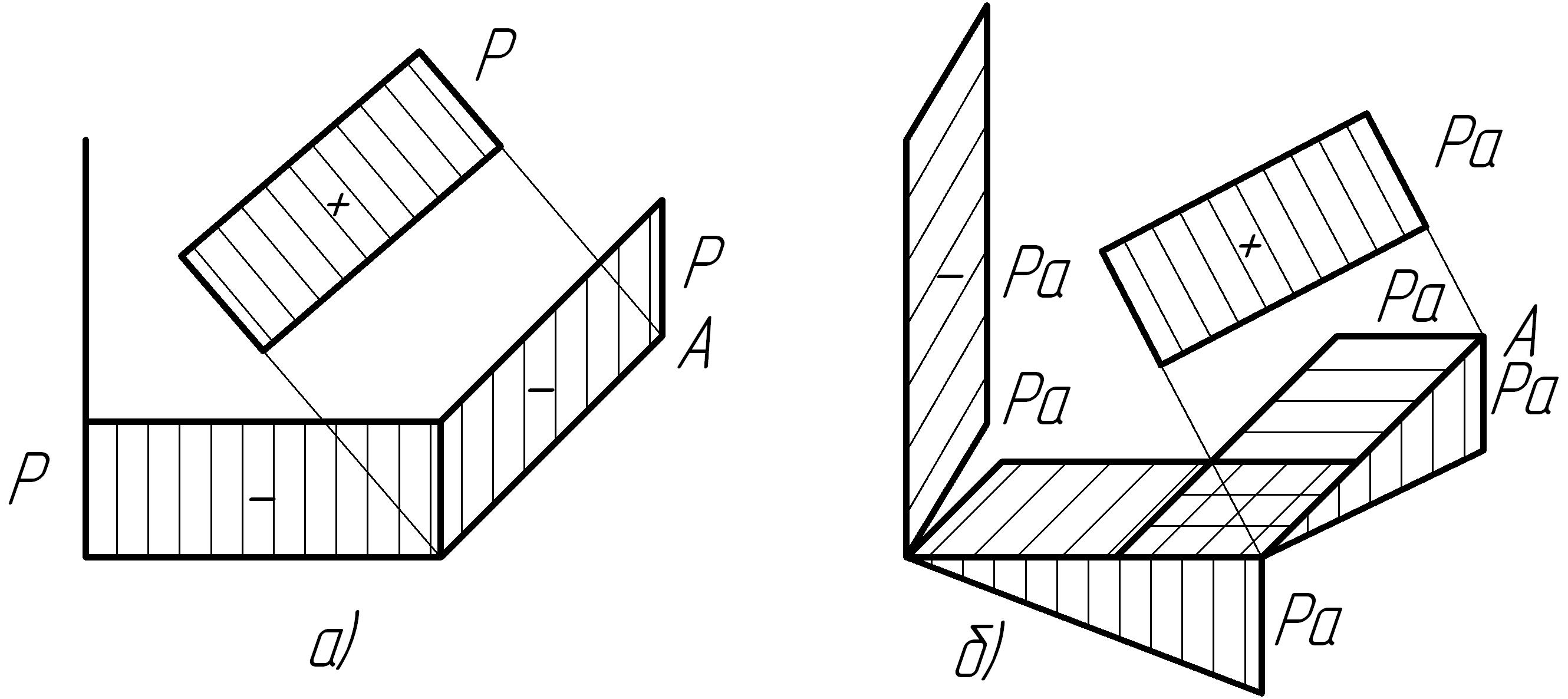
Рис. 7.19. Совмещенные эпюры внутренних силовых факторов:
а) эпюра сил
б) эпюра моментов
Для проверки правильности построения эпюр применяются те же правила, что и при изгибе балок и в рамах.
Опасное сечение
выбирается преимущественно по эпюре
моментов. В данном случае опасным
сечением является сечение в заделке,
где
![]() ;
;
![]() ,
,
![]() .
.
Для закрепления материала студенту рекомендуется самостоятельно построить эпюры внутренних силовых факторов для отдельных схем задачи 10.
