- •5. Порядок решения задач
- •5.1. Составление расчетной схемы
- •5.2. Статически определимая система и нахождение реакций опор
- •5.3. Определение количества участков
- •5.4. Составление аналитического выражения внутренних силовых
- •5.5. Построение эпюр внутренних силовых факторов по составленных аналитическим выражениям
- •5.6. Проверка правильности построения эпюр
- •5.7. Определение опасного сечения
- •6. Задачи для выполнения практических работ
- •7. Примеры решения задач
- •8. Напряженное и деформированное состояние при сложном нагружении. Гипотезы предельных состояний
- •9. Потенциальная энергия деформаций, определение перемещений. Расчет статически неопределимых систем
- •10. Устойчивость деформированного состояния
- •11. Местные и контактные напряжения. Прочность при переменных нагрузках
- •12. Сложное сопротивление
- •12.1. Понятие о сложном сопротивлении
- •12.2. Косой изгиб
- •12.3. Внецентренное растяжение (сжатие)
- •Максимальное напряжение при внецентренном растяжении (рис.12.2)
- •12.4. Изгиб с кручением Условие прочности при изгибе с кручением круглоёго стержня
- •12.5. Методика решения задач
- •13. Основы расчета на выносливость
- •Пульсационный (отнулевой) цикл (частный случай ассиметричного цикла)
- •13.1. Методика решения задач
- •14. Продольный изгиб
- •14.1. Методика решения задач
- •14.2. Задачи для самостоятельного решения
- •Наталья Александровна Лазуткина Ольга Григорьевна Кокорева
- •280101.65 «Безопасность жизнедеятельности в техносфере».
- •Муромский институт (филиал)
5.7. Определение опасного сечения
Как было указано выше, целью составления аналитических функций и построения эпюр внутренних силовых факторов является нахождение опасного сечения при расчете конструкции на прочность. Опасное сечение определяется по максимальному эквивалентному значению расчетного внутреннего силового фактора. Конкретные случаи такого определения будут обсуждены при расчетах на прочность.
6. Задачи для выполнения практических работ
Задача 1
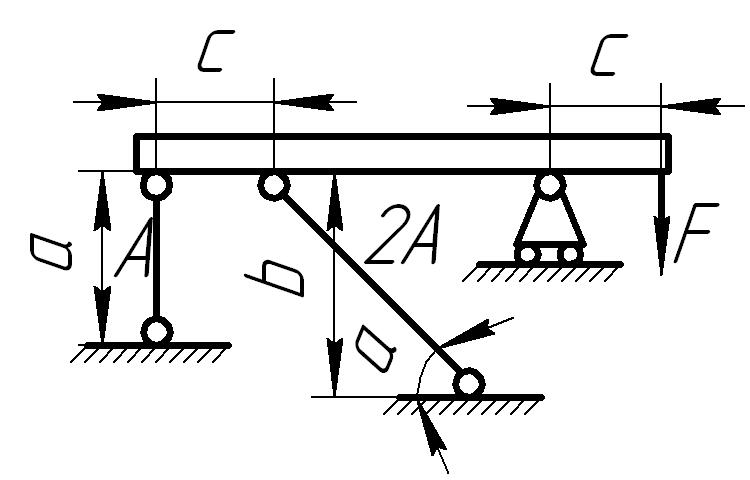
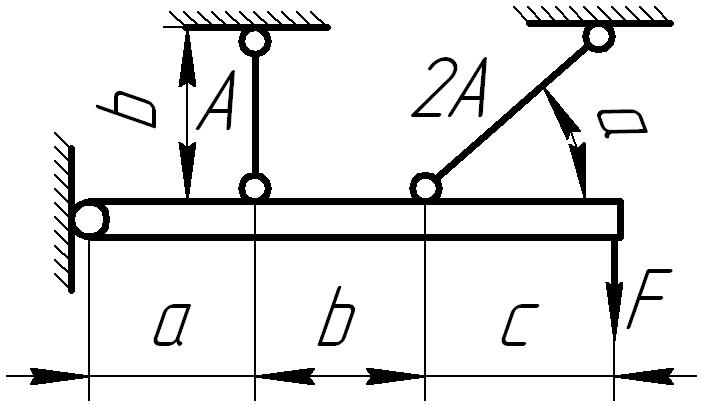
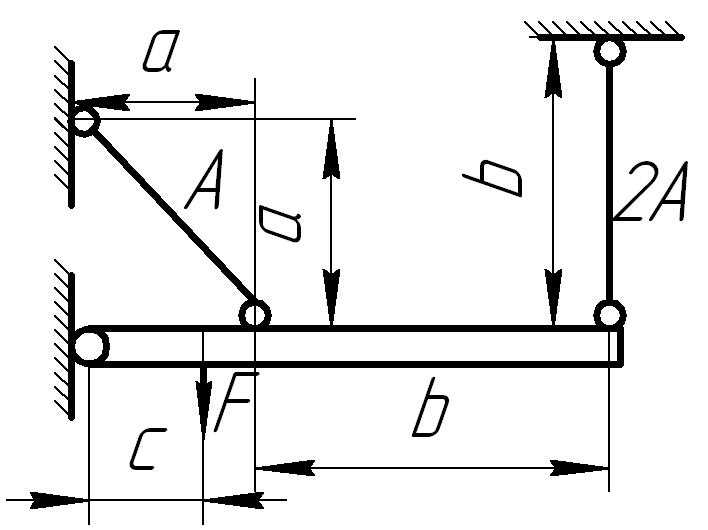
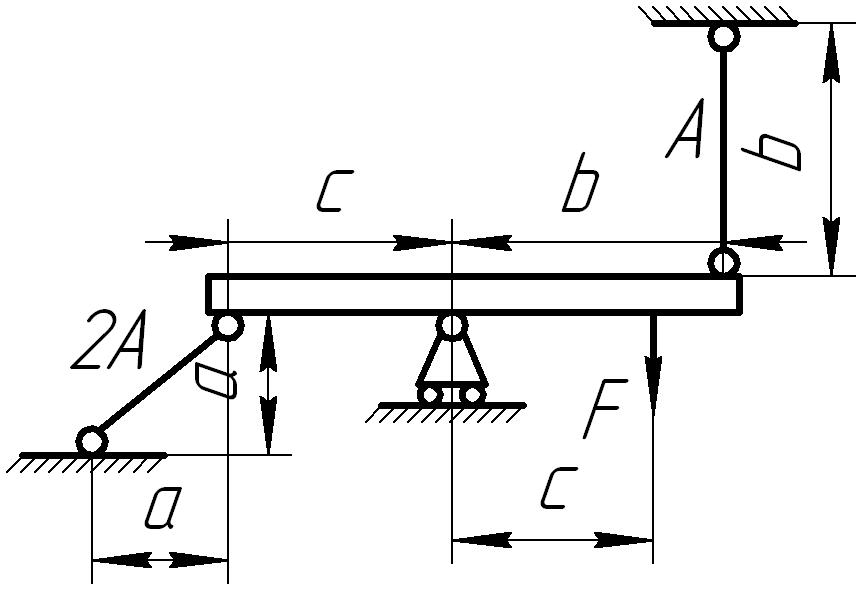
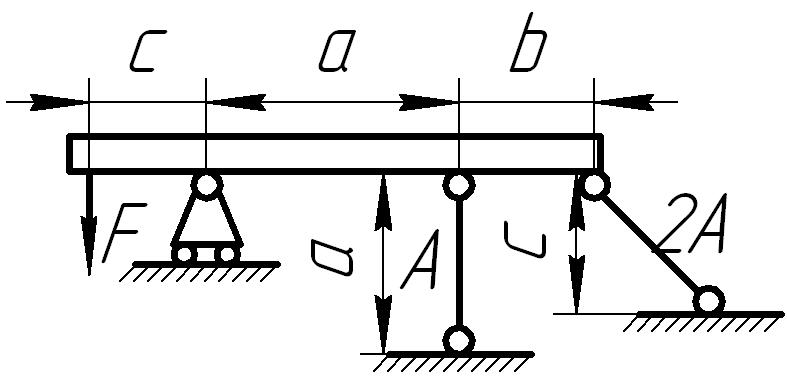
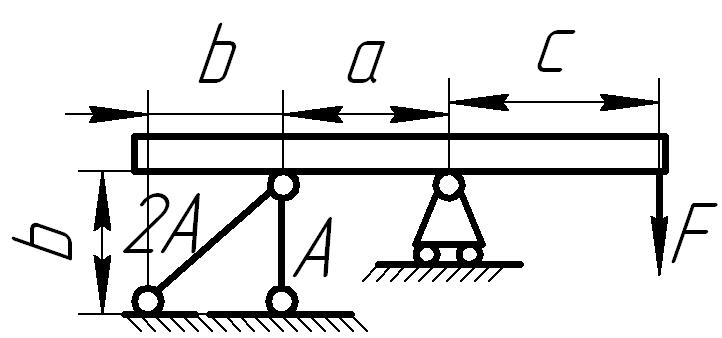
Абсолютно жесткий горизонтально расположенный брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис. 6.1). Один стержень имеет поперечное сечение А, другой — 2А. На брус действует вертикальная сила F, приложенная в указанной на рисунке точке. Требуется:
1) найти усилия и напряжения в стержнях, выразив их через силу F;
2) найти допускаемую нагрузку Fдоп , приравняв большее из напряжений в двух стержнях допускаемому напряжению [σ] = 160 МПа;
3) найти предельную грузоподъемность системы Fт и допускаемую нагрузку Fдоп, если предел текучести σт=240 МПа и запас прочности s= 1,5;
4) сравнить величины Fдоп, полученные при расчете по допускаемым напряжениям (п. 2) и допускаемым нагрузкам (п. 3). Данные взять из табл. 6.1.
Таблица 6.1
Варианты |
Данные величины |
Варианты |
Данные величины |
||||||||
А104, м² |
a, м |
b, м |
c, м |
угол α, рад |
А104, м² |
a, м |
b, м |
c, м |
угол α, рад |
||
1 |
10 |
2,1 |
3,1 |
1,0 |
π/4 |
6 |
12 |
2,6 |
3,6 |
1,2 |
π/4 |
2 |
10 |
2,2 |
3,2 |
1,0 |
π/4 |
7 |
13 |
2,7 |
3,7 |
1,3 |
π/4 |
3 |
11 |
2,3 |
3,3 |
1,1 |
π/4 |
8 |
13 |
2,8 |
3,8 |
1,3 |
π/4 |
4 |
11 |
2,4 |
3,4 |
1,1 |
π/4 |
9 |
14 |
2,9 |
3,9 |
1,4 |
π/4 |
5 |
12 |
2,5 |
3,5 |
1,2 |
π/4 |
10 |
14 |
3,0 |
4,0 |
1,4 |
π/4 |
1 |
|
6 |
|
2 |
|
7 |
|
3 |
|
8 |
|
4 |
|
9 |
|
5 |
|
10 |
|
Рис. 6.1
Указания. Для определения двух неизвестных усилий в стержнях следует составить одно уравнение статики и одно уравнение деформаций.
Для ответа на третий вопрос задачи следует иметь в виду, что в одном из стержней напряжение больше чем в другом; условно назовем этот стержень первым. При увеличении нагрузки напряжение в первом стержне достигнет предела текучести ранее, чем во втором. Когда это произойдет, напряжение в первом стержне не будет некоторое время расти даже при увеличении нагрузки, система станет как бы статически определимой, нагруженной силой F (пока еще неизвестной) и усилием в первом стержне:
![]() . (6.1)
. (6.1)
При дальнейшем увеличении нагрузки напряжение и во втором стержне достигнет предела текучести:
![]() . (6.2)
. (6.2)
Написав уравнение статики и подставив в него значения усилий (6.1) и (6.2) найдем из этого уравнения предельную грузоподъемность Fт.
Задача 2
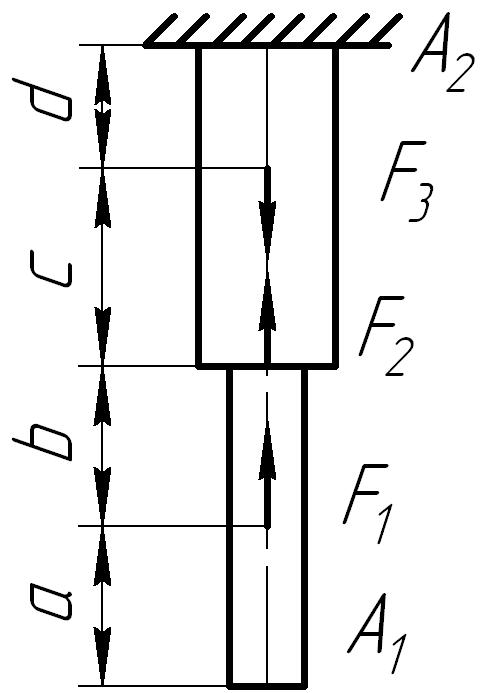
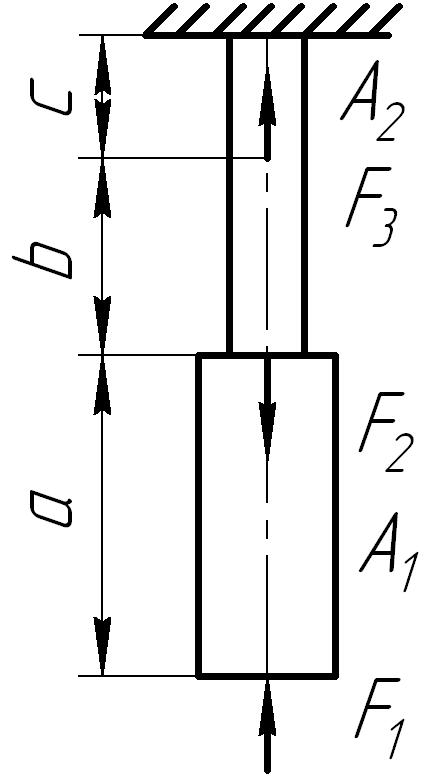
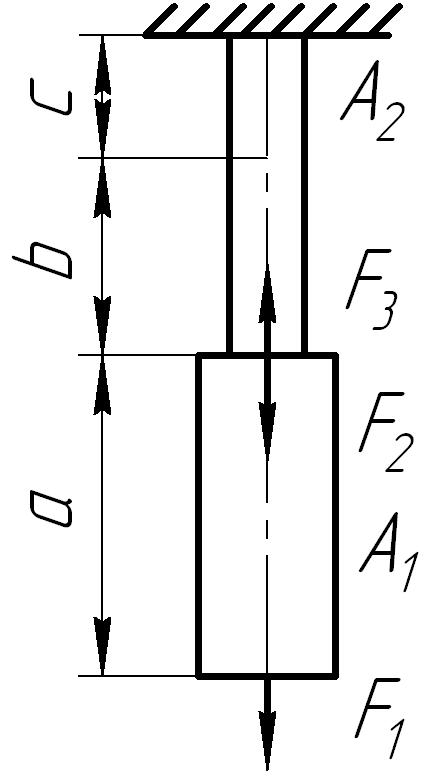
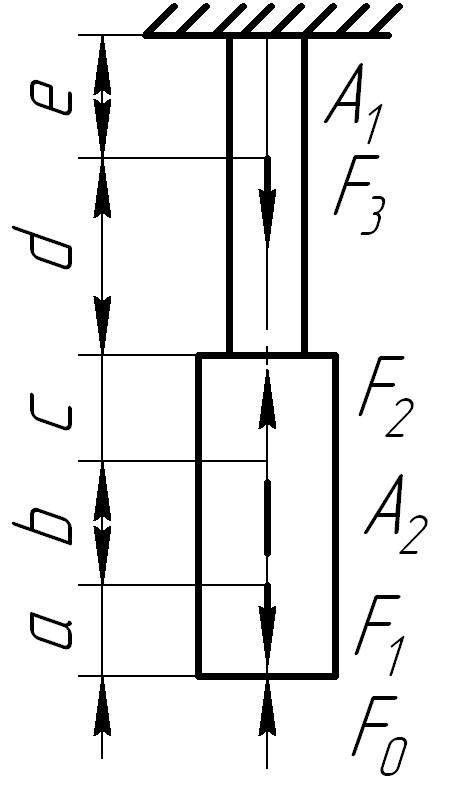
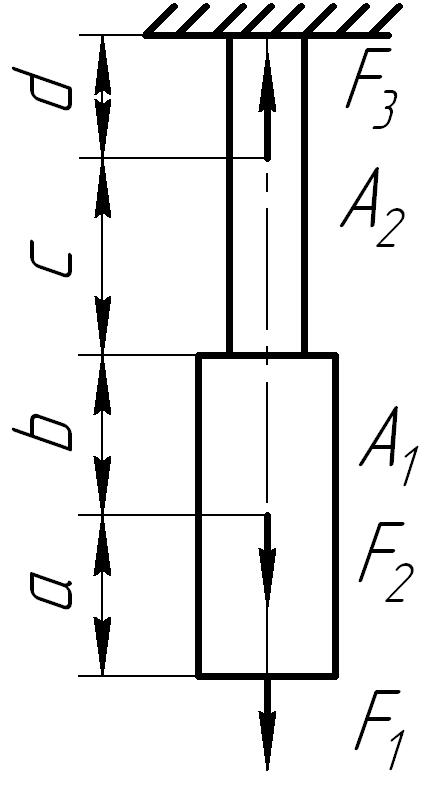
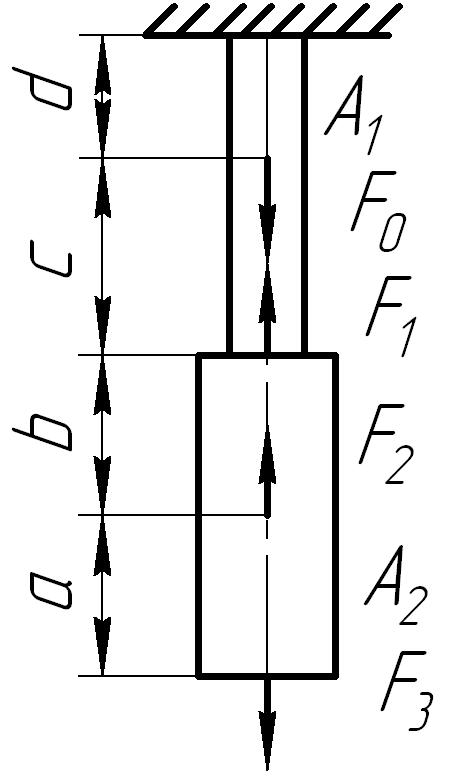
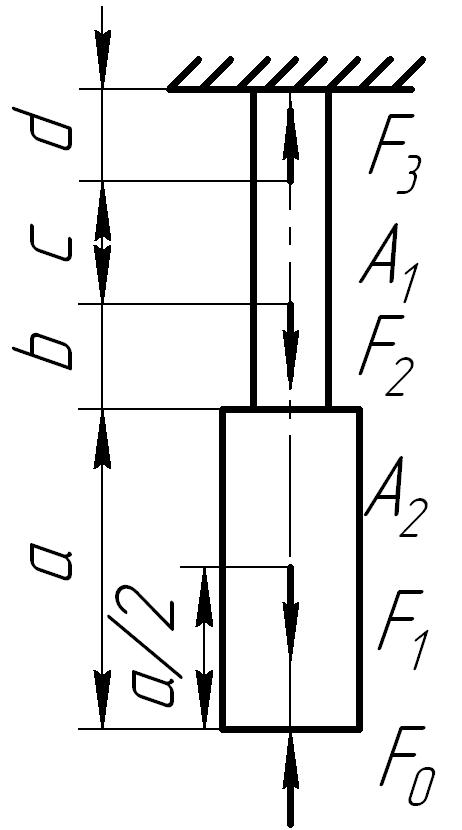
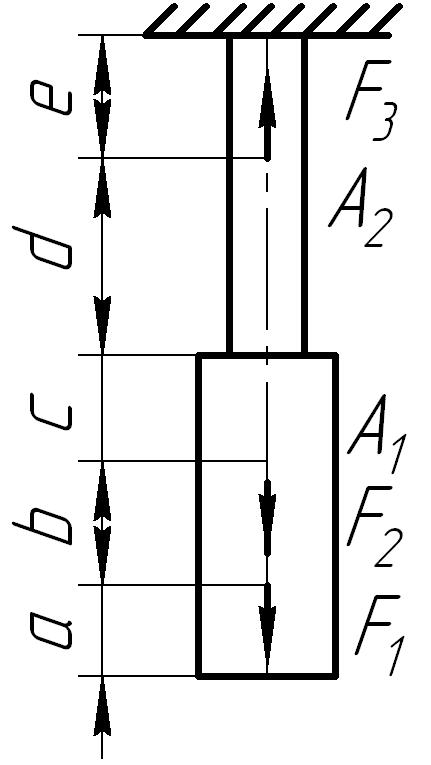
Для стального
бруса (рис. 6.2) построить эпюры продольных
сил, нормальных напряжений в поперечных
сечениях бруса и перемещений этих
сечений, а также определить потенциальную
энергию деформации. Принять
![]() МПа,
МПа,
![]() ,
,
![]() .
Данные взять из табл. 6.2.
.
Данные взять из табл. 6.2.
Таблица 6.2
Вариант |
F1, кН |
F2, кН |
F3, кН |
A1, см2 |
A2, см2 |
a, м |
b, м |
c, м |
1 |
32 |
16 |
9 |
1,8 |
2,5 |
0,2 |
0,6 |
0,4 |
2 |
30 |
10 |
5 |
1,7 |
2,8 |
0,25 |
0,55 |
0,45 |
3 |
20 |
8 |
14 |
1,2 |
1,8 |
0,7 |
0,25 |
0,4 |
4 |
18 |
10 |
15 |
1,3 |
1,7 |
0,6 |
0,2 |
0,5 |
5 |
11 |
26 |
30 |
1,5 |
3 |
0,3 |
0,7 |
0,3 |
6 |
17 |
16 |
20 |
1,2 |
1,9 |
0,25 |
0,6 |
0,25 |
7 |
29 |
12 |
10 |
2,2 |
1,9 |
0,15 |
0,10 |
0,15 |
8 |
31 |
14 |
12 |
2,4 |
2,0 |
0,2 |
0,15 |
0,20 |
9 |
12 |
15 |
9 |
1,9 |
1,7 |
0,5 |
0,3 |
0,5 |
10 |
23 |
21 |
15 |
2,1 |
1,8 |
0,6 |
0,2 |
0,6 |
11 |
31 |
24 |
15 |
2,7 |
2,4 |
0,1 |
0,6 |
0,1 |
12 |
21 |
15 |
8 |
2,1 |
1,9 |
0,2 |
0,4 |
0,2 |
13 |
17 |
13 |
6 |
1,1 |
1,5 |
0,4 |
0,4 |
0,6 |
14 |
20 |
17 |
10 |
1,3 |
1,9 |
0,5 |
0,5 |
0,7 |
15 |
10 |
12 |
13 |
0,9 |
0,7 |
0,8 |
0,4 |
0,3 |
16 |
17 |
19 |
20 |
1,6 |
1,4 |
0,6 |
0,35 |
0,25 |
17 |
40 |
55 |
24 |
2,8 |
3,4 |
0,4 |
0,4 |
0,5 |
18 |
31 |
46 |
20 |
1,9 |
2,5 |
0,35 |
0,35 |
0,6 |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
Рис. 6.2
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
Рис. 6.2
16 |
|
17 |
|
18 |
|
Рис. 6.2
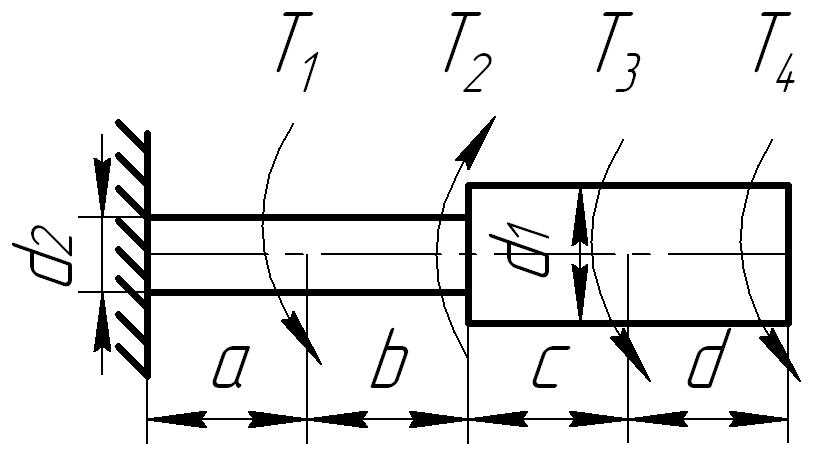
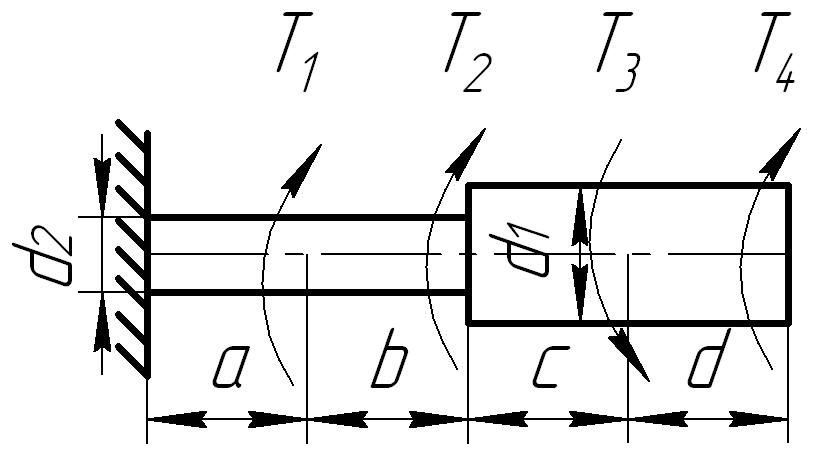
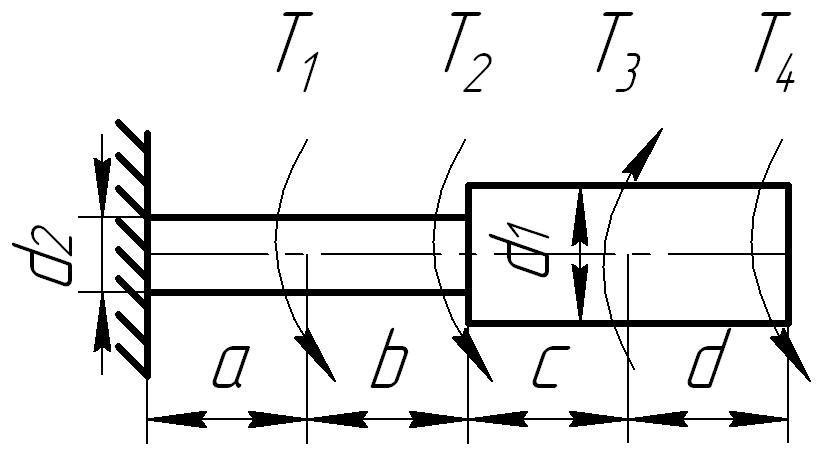
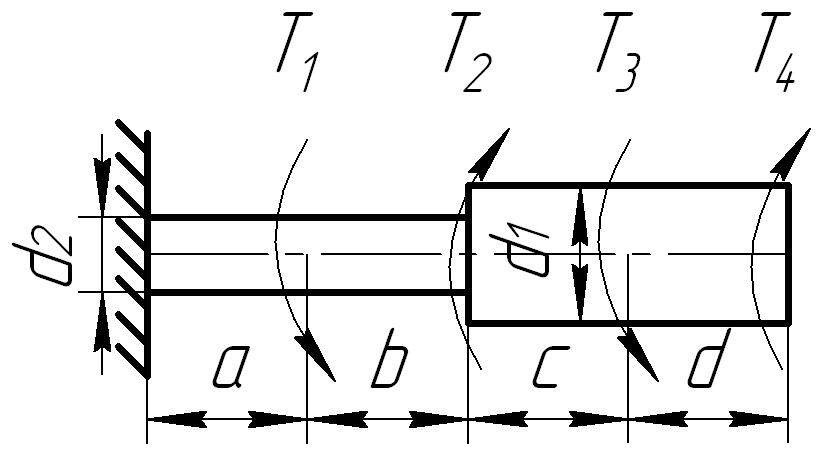
Задача 3
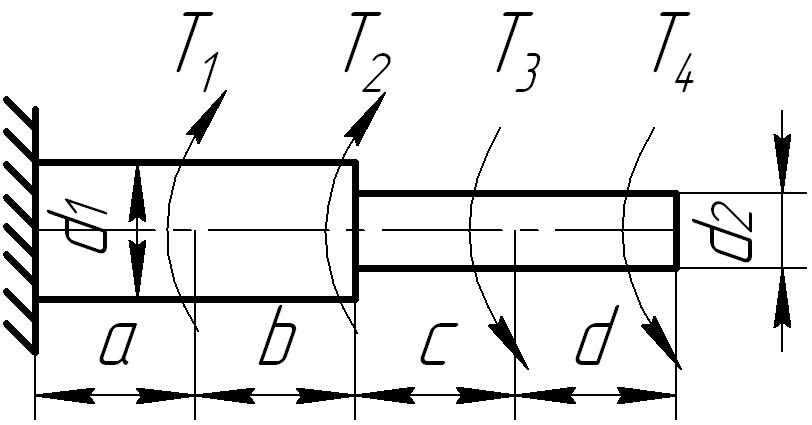
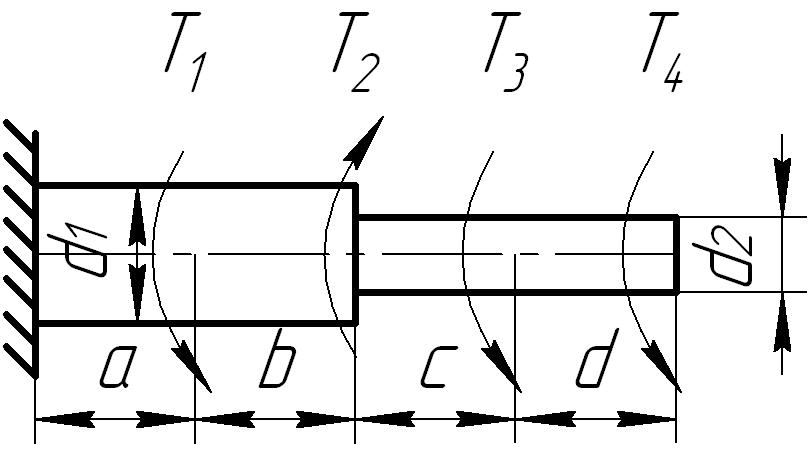
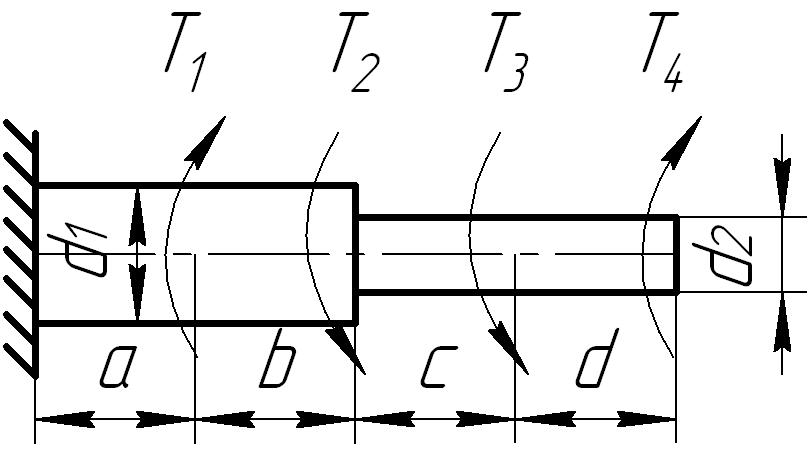
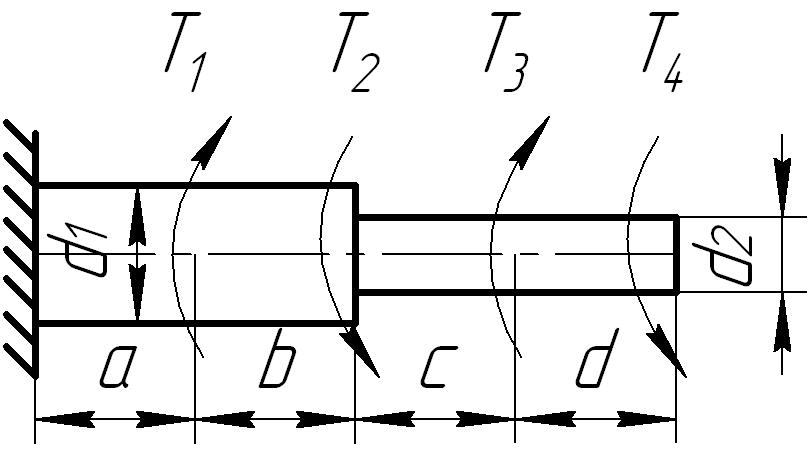
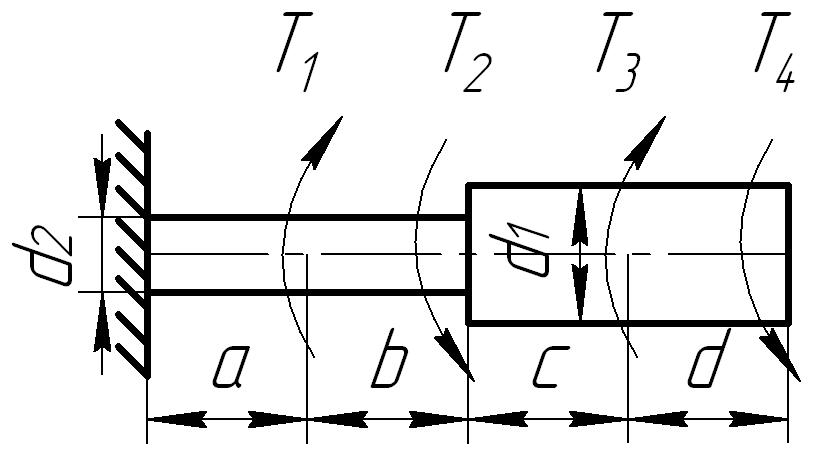
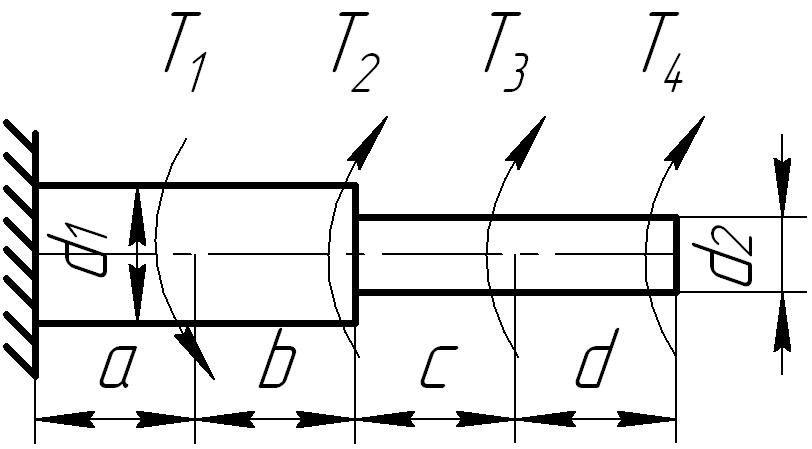
К стальному ступенчатому валу, имеющему сплошное поперечное сечение, приложены четыре момента (рис. 6.3) . Левый конец вала жестко закреплен в опоре, а правый конец — свободен и его торец имеет угловые перемещения относительно левого конца. Требуется:
1) построить эпюру крутящих моментов по длине вала;
2) при заданном значении допускаемого напряжения на кручение определить диаметры d1 и d2 вала из расчета на прочность, полученные значения округлить до числа, кратного 5 мм;
3) построить эпюру действительных напряжений кручения по длине вала;
4) построить эпюру углов закручивания, приняв G ≈ 0,4 Е.
Данные взять из
табл. 6.3 (![]() ).
).
1 |
|
2 |
|
Рис. 6.3
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
Рис. 6.3
Таблица 6.3
Вариант |
Расстояния, м |
Моменты, кН·м |
[τ] МПа |
|||||
а |
b |
с |
T1 |
T2 |
T3 |
T4 |
||
1 |
1,0 |
1,0 |
1,0 |
5,1 |
2,1 |
1,1 |
0,1 |
30 |
2 |
1,1 |
1,1 |
1,1 |
5,2 |
2,2 |
1,2 |
0,2 |
30 |
3 |
1,2 |
1,2 |
1,2 |
5,3 |
2,3 |
1,3 |
0,3 |
35 |
4 |
1,3 |
1,3 |
1,3 |
5,4 |
2,4 |
1,4 |
0,4 |
35 |
5 |
1,4 |
1,4 |
1,4 |
5,5 |
2,5 |
1,5 |
0,5 |
40 |
6 |
1,5 |
1,5 |
1,5 |
5,6 |
2,6 |
1,6 |
0,6 |
40 |
7 |
1,6 |
1,6 |
1,6 |
5,7 |
2,7 |
1,7 |
0,7 |
45 |
8 |
1,7 |
1,7 |
1,7 |
5,8 |
2,8 |
1,8 |
0,8 |
45 |
9 |
1,8 |
1,8 |
1,8 |
5,9 |
2,9 |
1,9 |
0,9 |
50 |
10 |
1,9 |
1,9 |
1,9 |
6,0 |
3,0 |
2,0 |
1,0 |
50 |
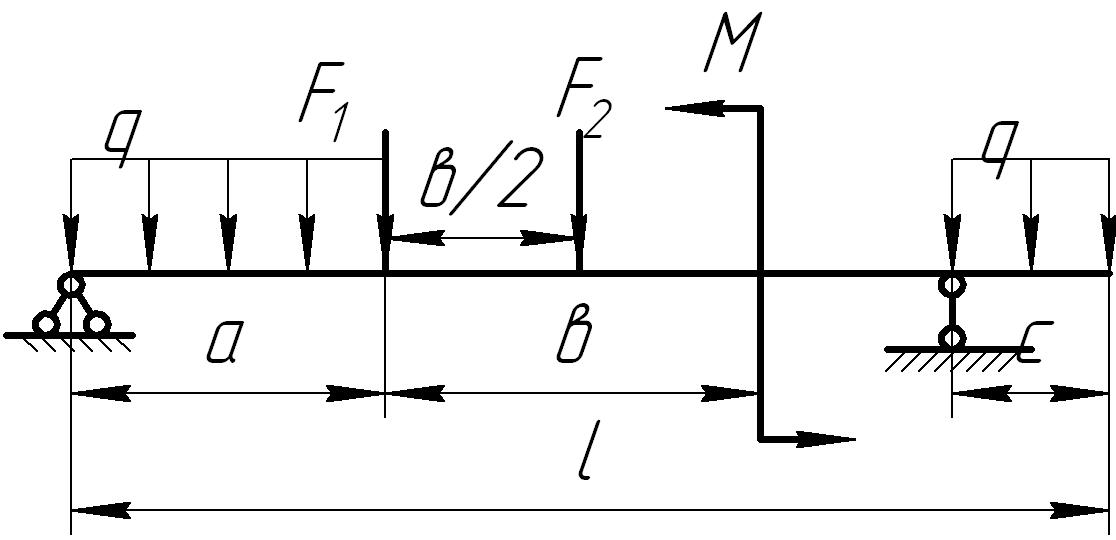
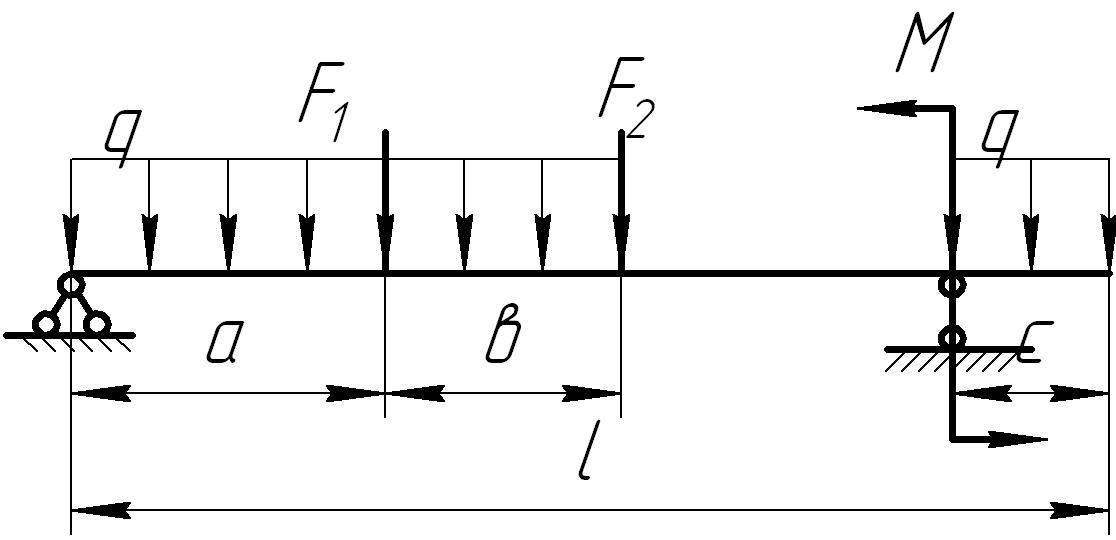
Задача 4
Для заданных схем
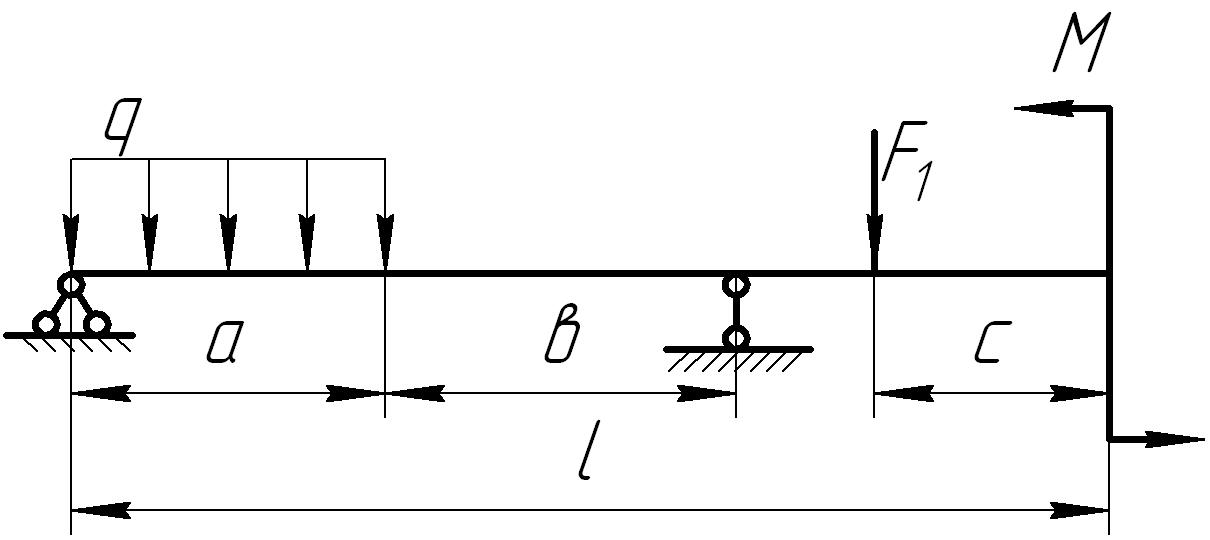
балок (рис. 6.4) требуется написать
выражения
![]() и
и
![]() для каждого участка и общем виде,
построить эпюры
и
,
найти
для каждого участка и общем виде,
построить эпюры
и
,
найти
![]() и подобрать:
и подобрать:
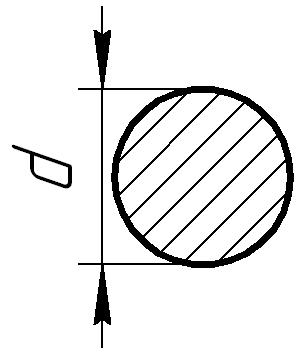
а) деревянную балку
круглого поперечного сечения при
![]() кГ/см2;
кГ/см2;
б) стальную балку
двутаврового поперечного сечения при
![]() кГ/см2.
кГ/см2.
Данные взять из табл. 6.4
1 |
|
2 |
|
3 |
|
4 |
|
Рис. 6.4
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
Рис. 6.4
Таблица 6.4
Номер строки |
а (в м) |
(в м) |
|
|
М (в Нм) |
Сосредоточенная
сила
|
(в Н/м) |
1 |
1,1 |
6 |
1 |
1 |
1,0 |
1,0 |
1,0 |
2 |
1,2 |
7 |
2 |
2 |
2,0 |
2,0 |
2,0 |
3 |
1,3 |
13 |
3 |
3 |
0,3 |
0,3 |
0,3 |
4 |
1,4 |
14 |
4 |
4 |
0,4 |
0,4 |
0,4 |
5 |
1,5 |
15 |
5 |
5 |
0,5 |
0,5 |
0,5 |
6 |
1,6 |
16 |
3,6 |
1 |
0,6 |
0,6 |
0,6 |
7 |
1,7 |
17 |
4,7 |
2 |
0,7 |
0,7 |
0,7 |
8 |
1,8 |
18 |
3,8 |
3 |
0,8 |
0,8 |
0,8 |
9 |
1,9 |
19 |
5,9 |
4 |
0,9 |
0,9 |
0,9 |
10 |
2,0 |
20 |
9 |
5 |
1,0 |
1,0 |
1,0 |
![]() ;
;
![]() .
.
Задача 5
Стальной стержень
длиной
сжимается силой
(рис. 6.5). Стержень имеет различные схемы
закрепления концов (два типа) и различные
формы поперечного сечения (пять видов).
Всего десять типов задач. Для схем I,
III, V, VII,
IX коэффициент приведения
длины
![]() ,
для схем II, IV,
VI, VIII и X
–
,
для схем II, IV,
VI, VIII и X
–
![]() .
.
Требуется: 1) найти
размеры поперечного сечения при
допускаемом напряжении
![]() МПа (расчет производить последовательными
приближениями, предварительно, приняв
величину коэффициента
МПа (расчет производить последовательными
приближениями, предварительно, приняв
величину коэффициента
![]() );
);
2) найти числовое значение критической силы и коэффициент запаса устойчивости. Данные взять из табл. 6.5.
Тип схемы |
Схема зацепления концов стержня |
Тип схемы |
Схема зацепления концов стержня |
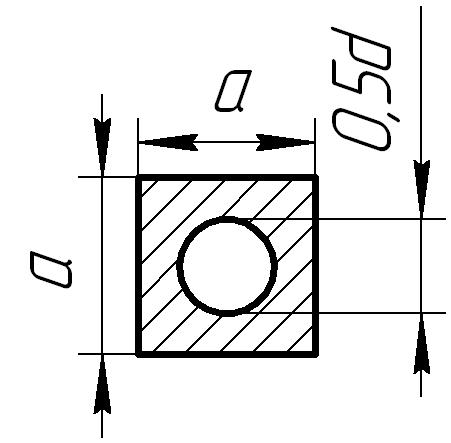
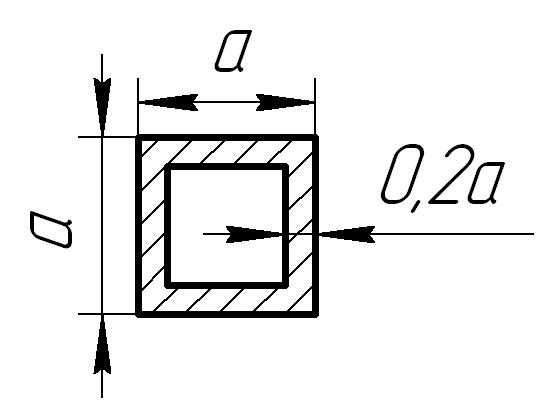
Форма сечения стержня |
I |
|
II |
|
|
III |
|
IV |
|
|
V |
|
VI |
|
|
VII |
|
VIII |
|
|
IX |
|
X |
|
|
Рис. 6.5
Таблица 6.5
Варианты |
Данные величины |
|
, кН |
, м |
|
1 |
80 |
2,0 |
2 |
160 |
2,1 |
3 |
240 |
2,2 |
4 |
320 |
2,3 |
5 |
400 |
2,4 |
6 |
480 |
2,3 |
7 |
560 |
2,2 |
8 |
640 |
2,1 |
9 |
720 |
2,0 |
10 |
800 |
1,9 |
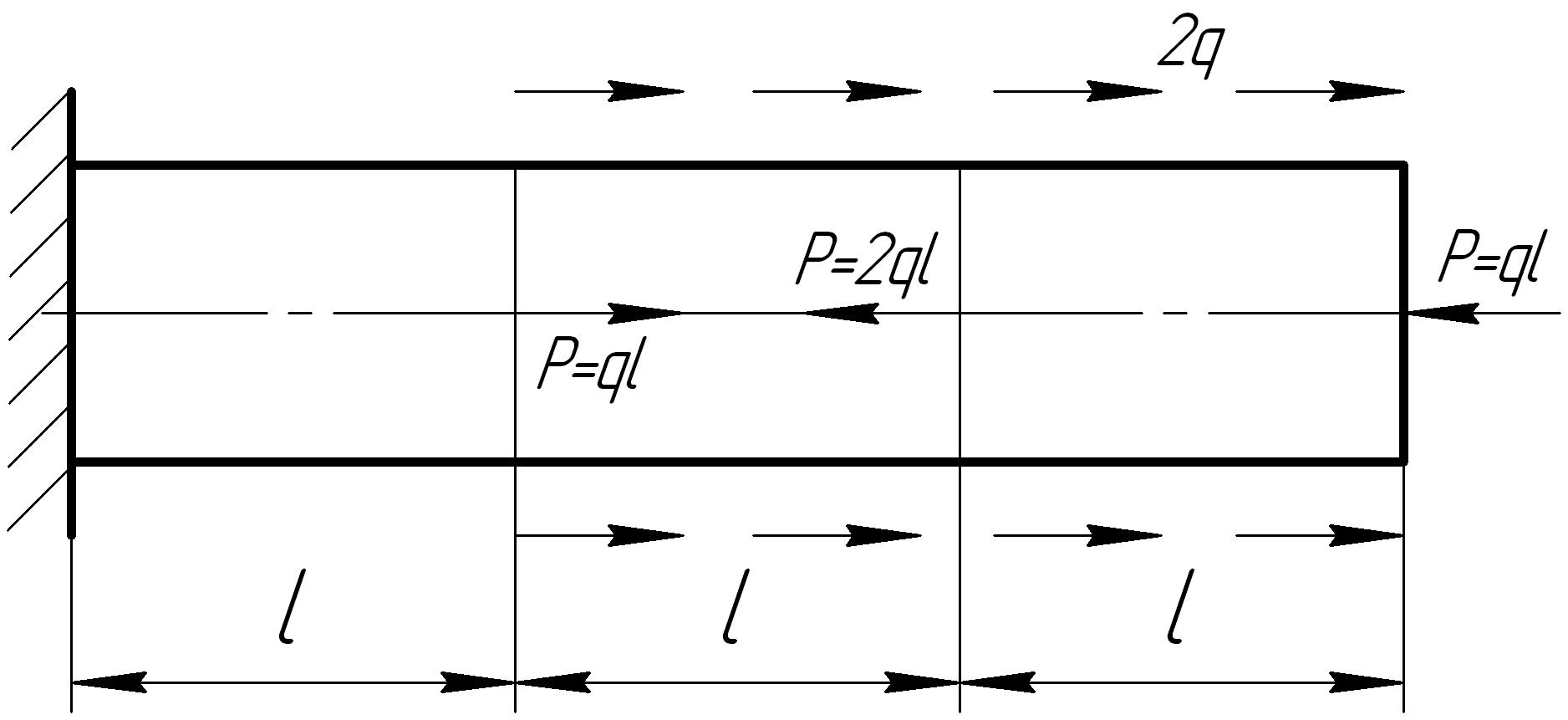
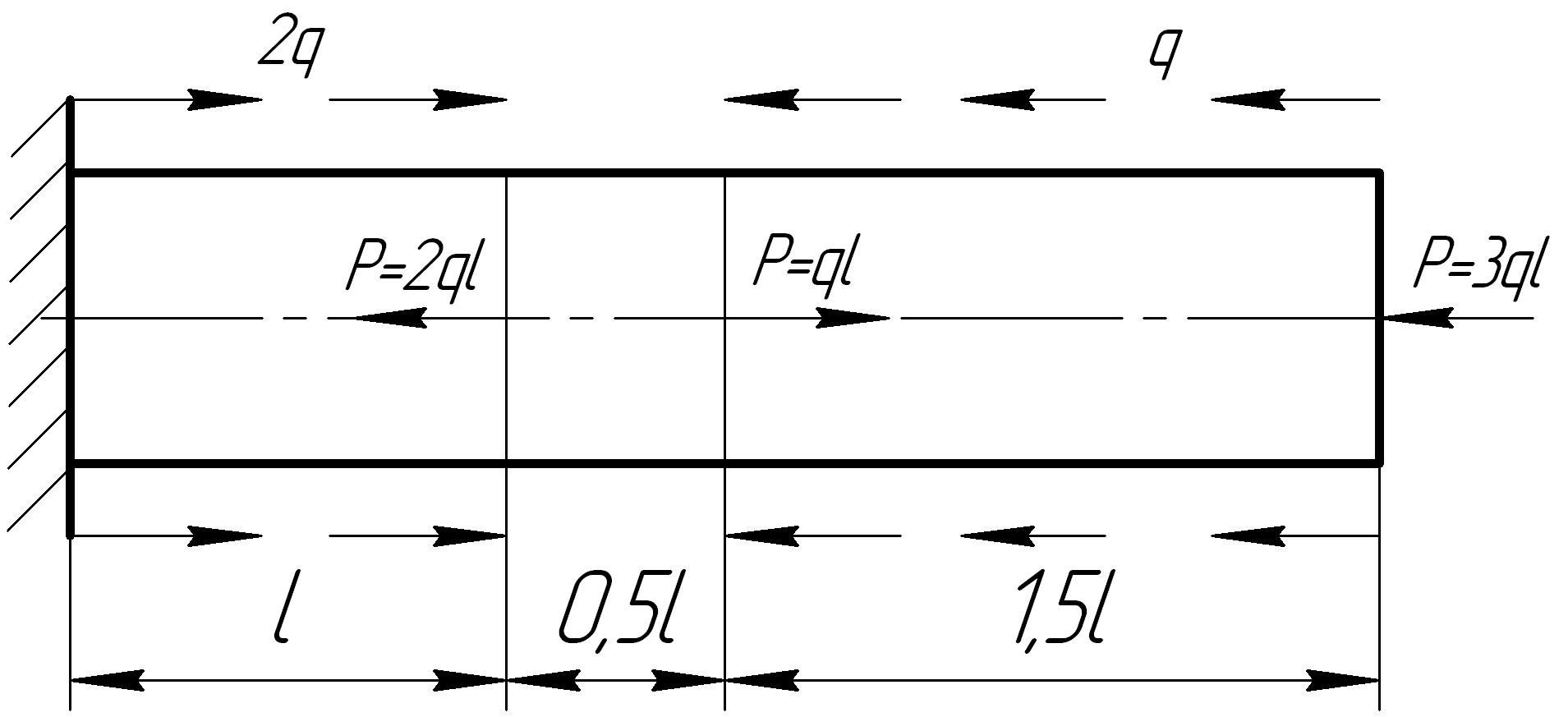
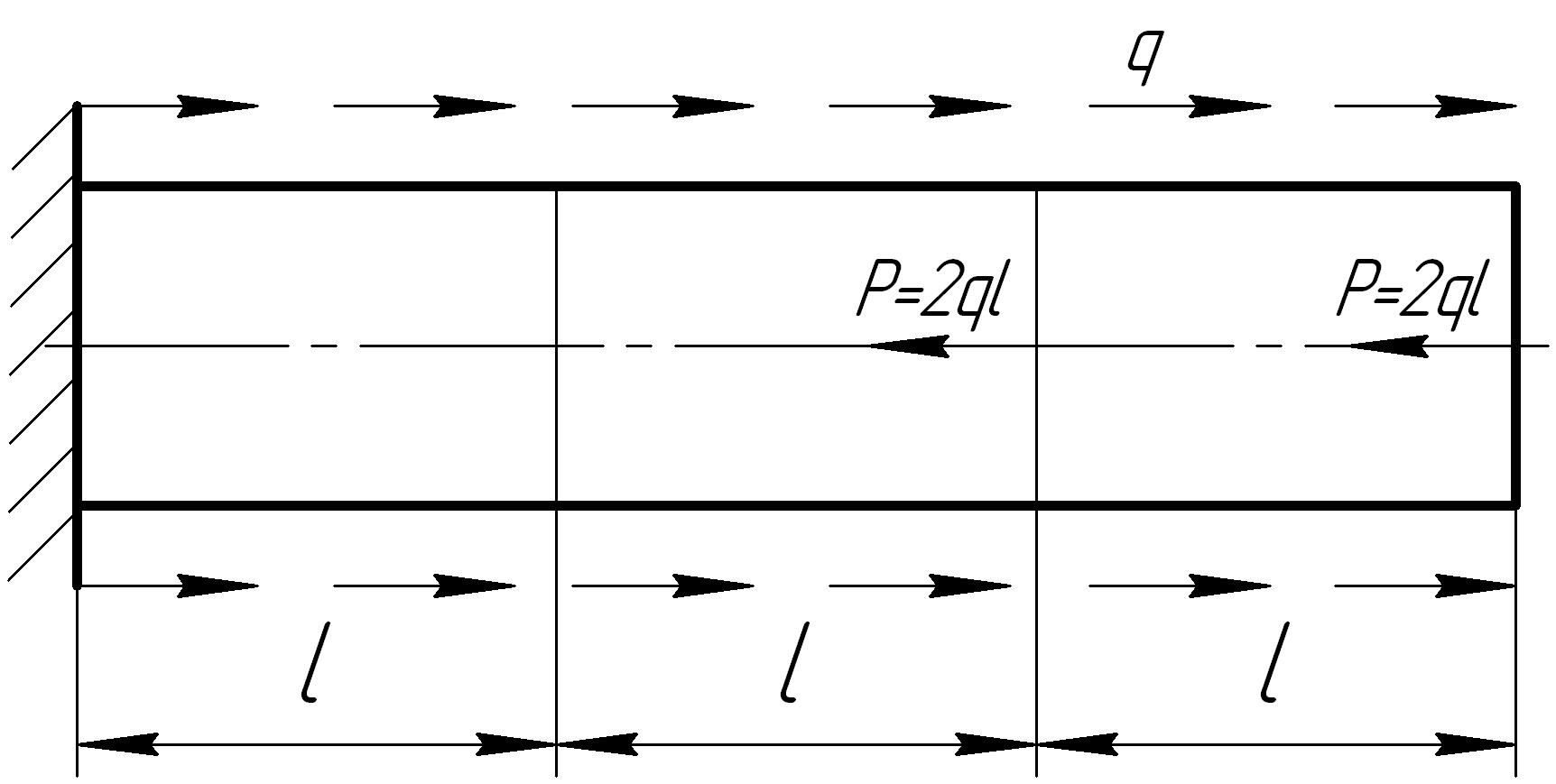
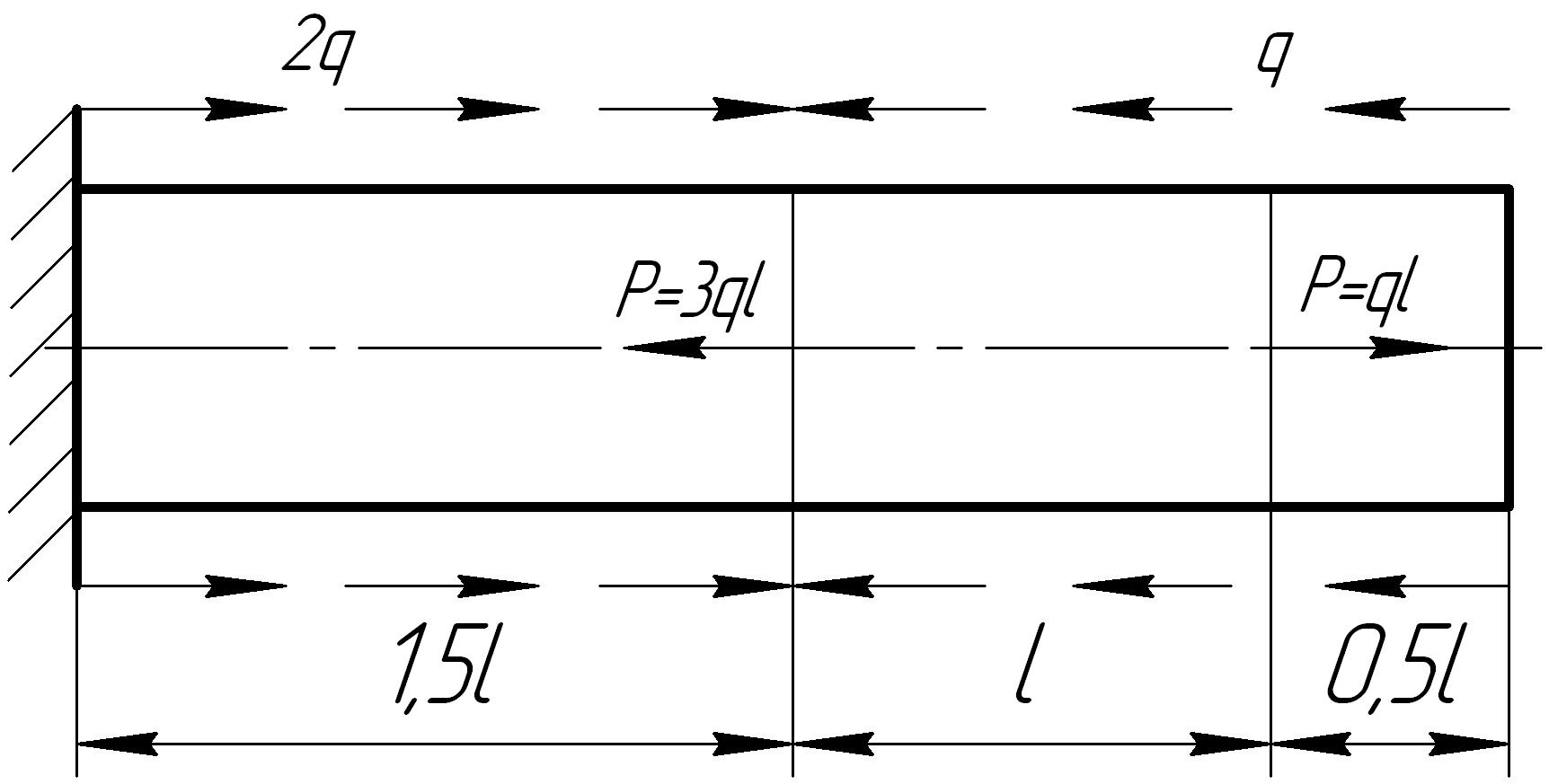
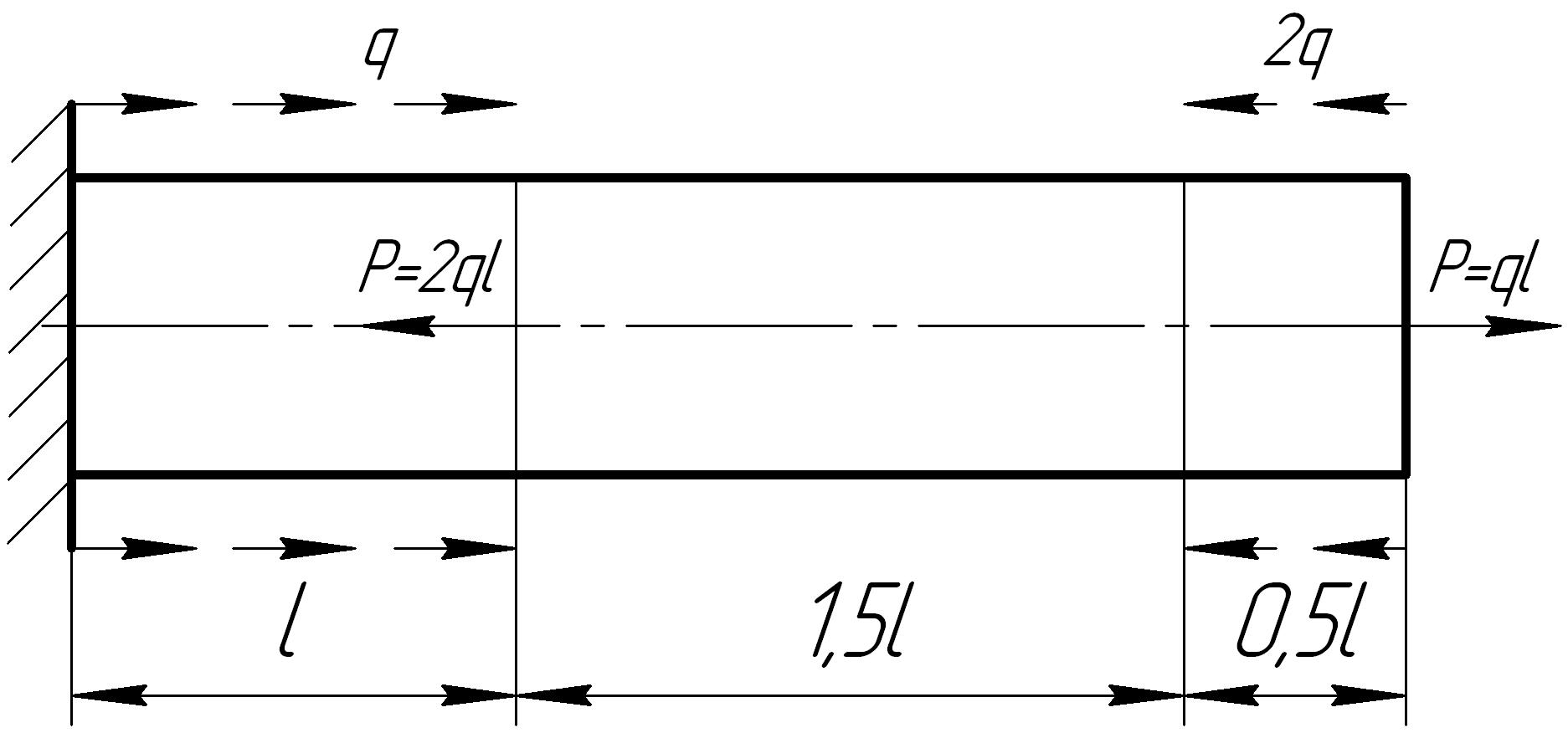
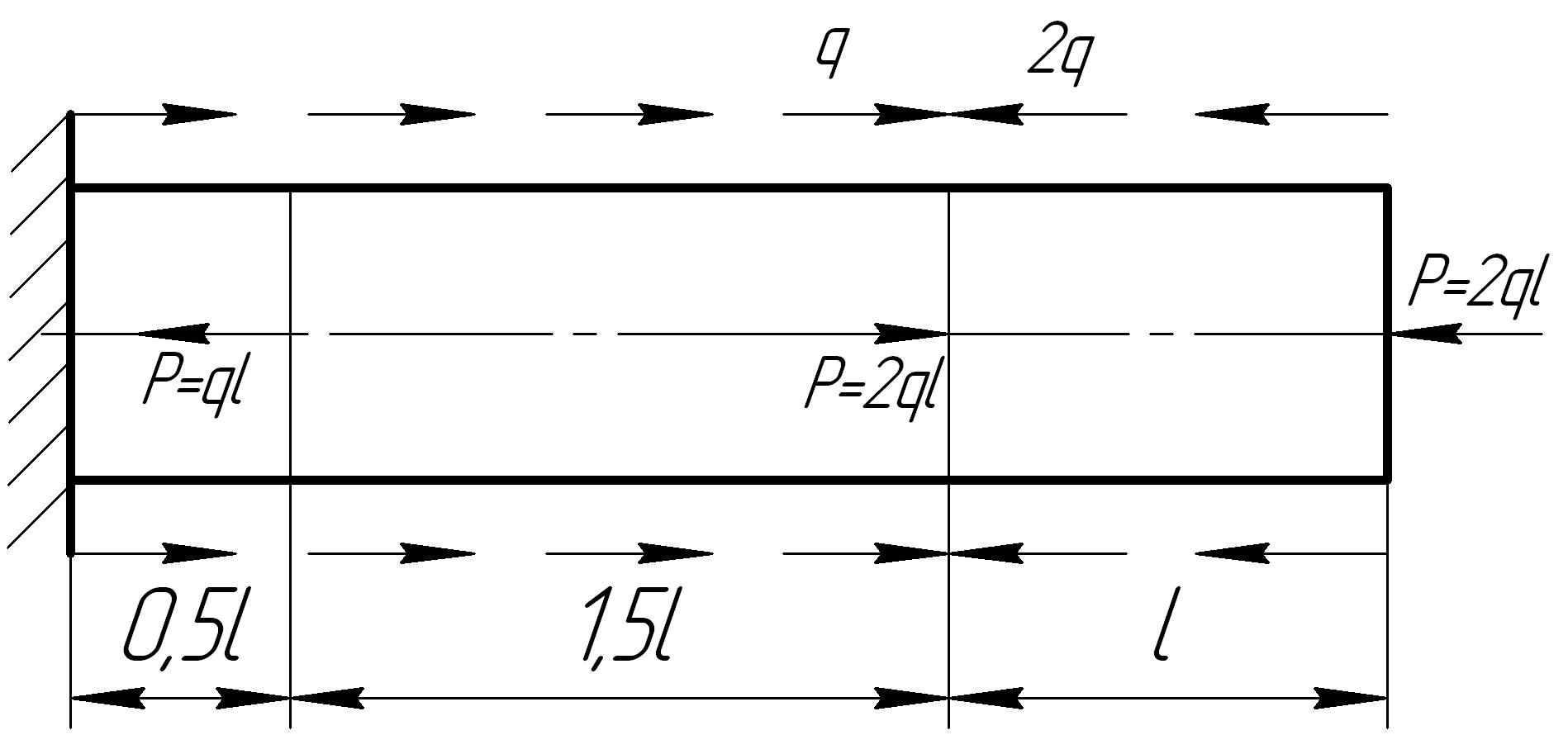
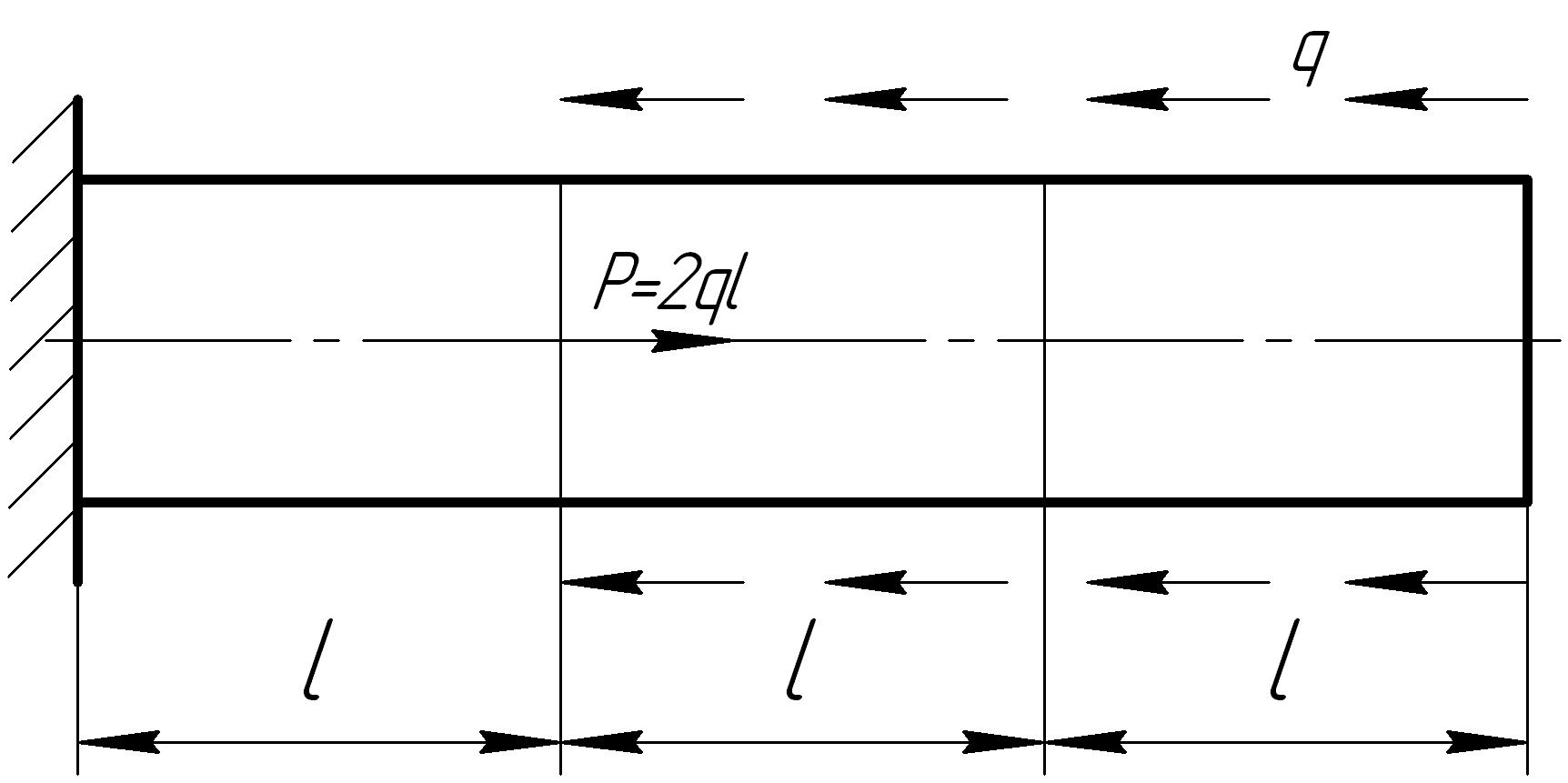
Задача 6
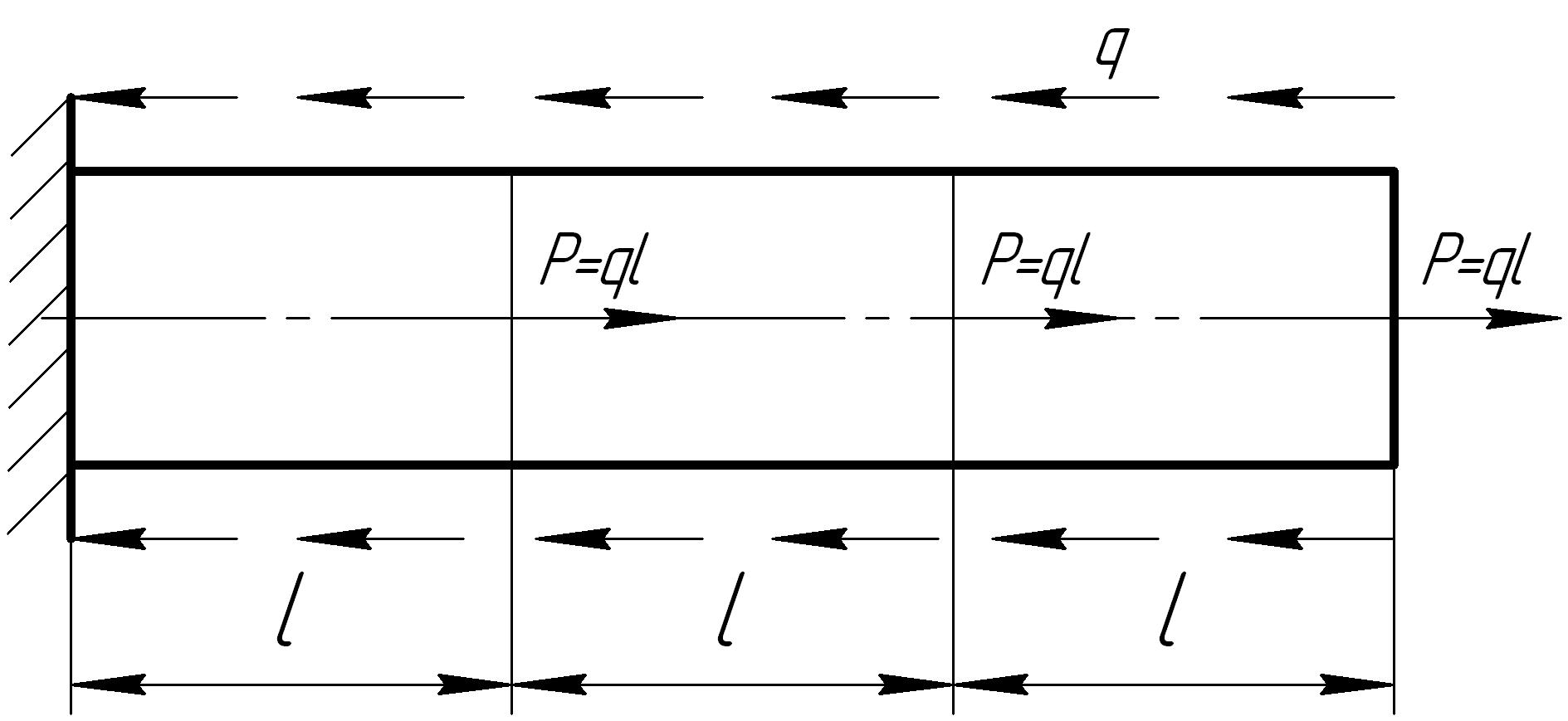
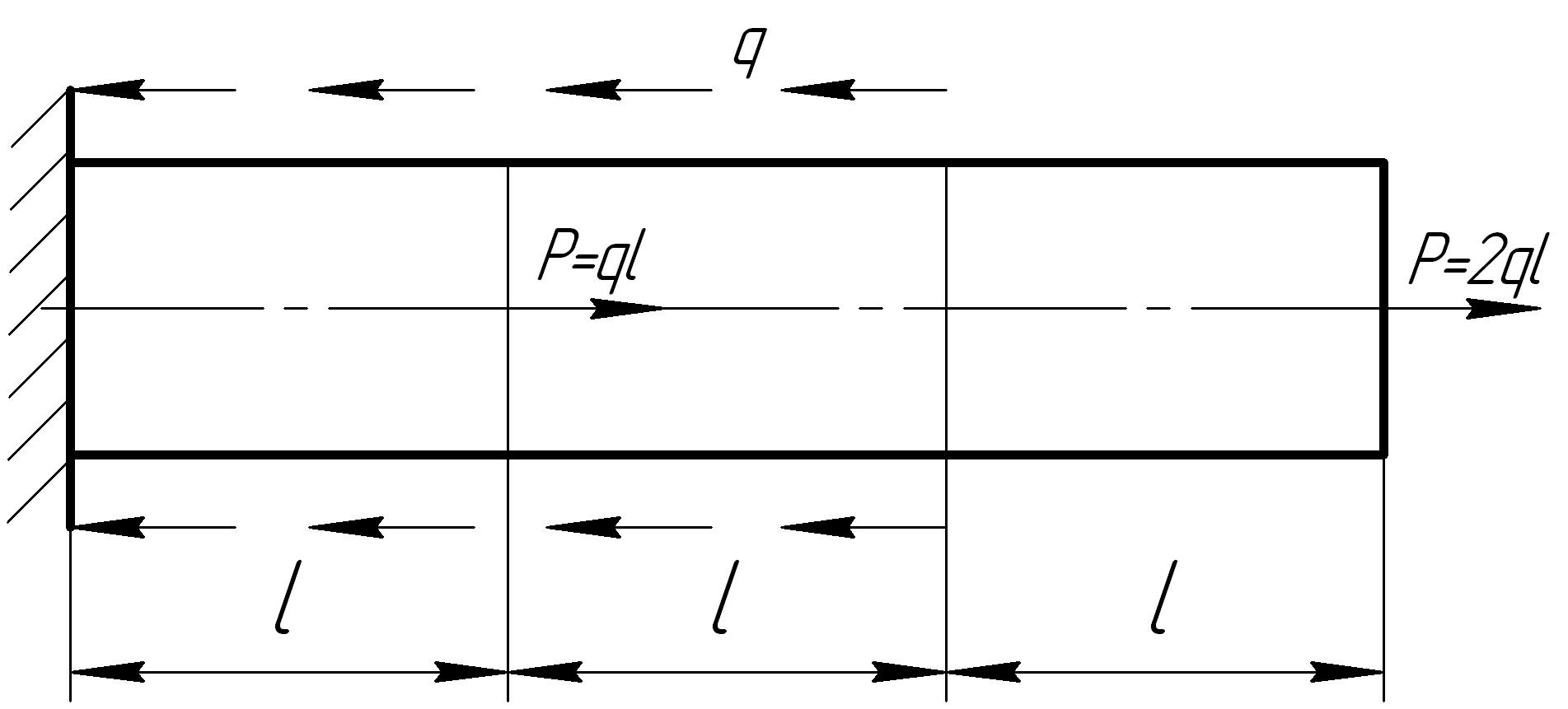
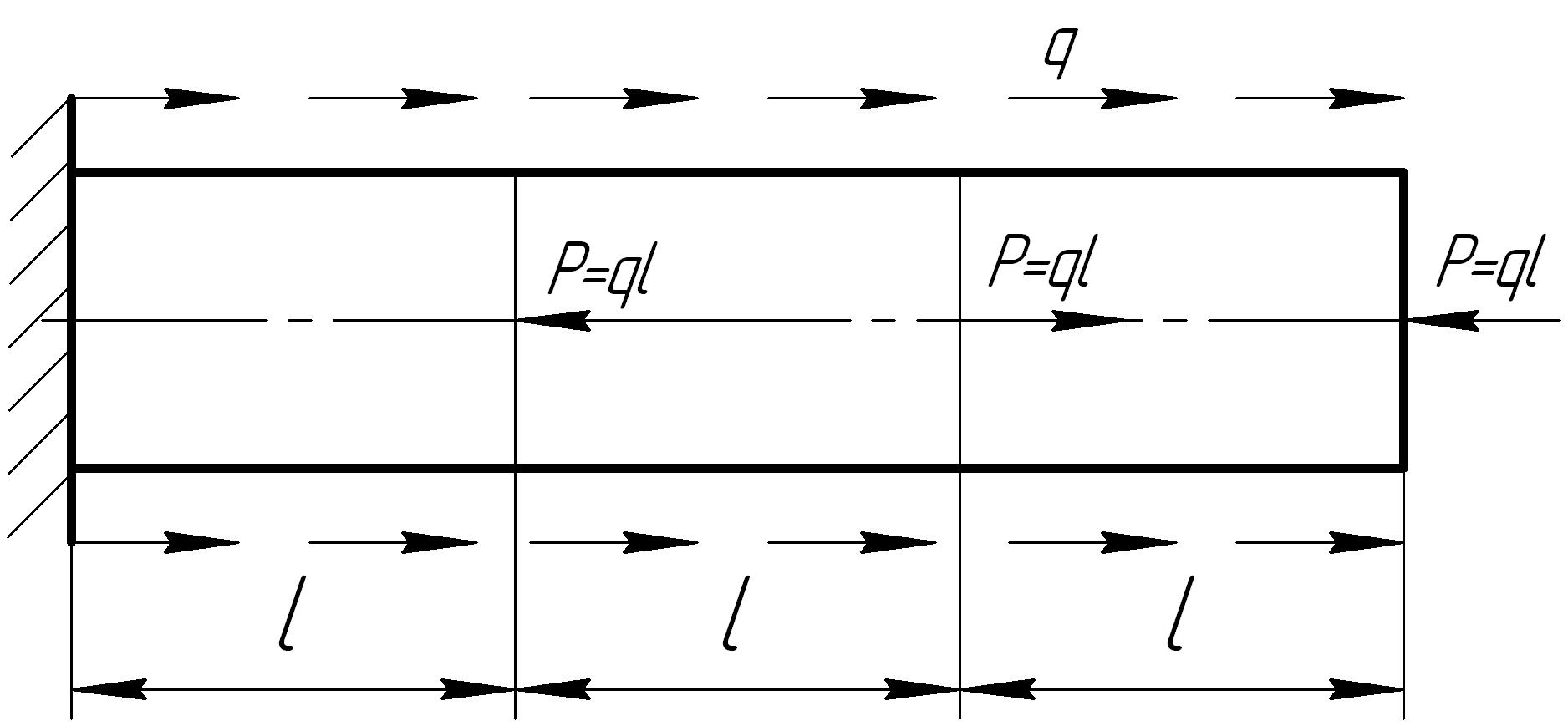
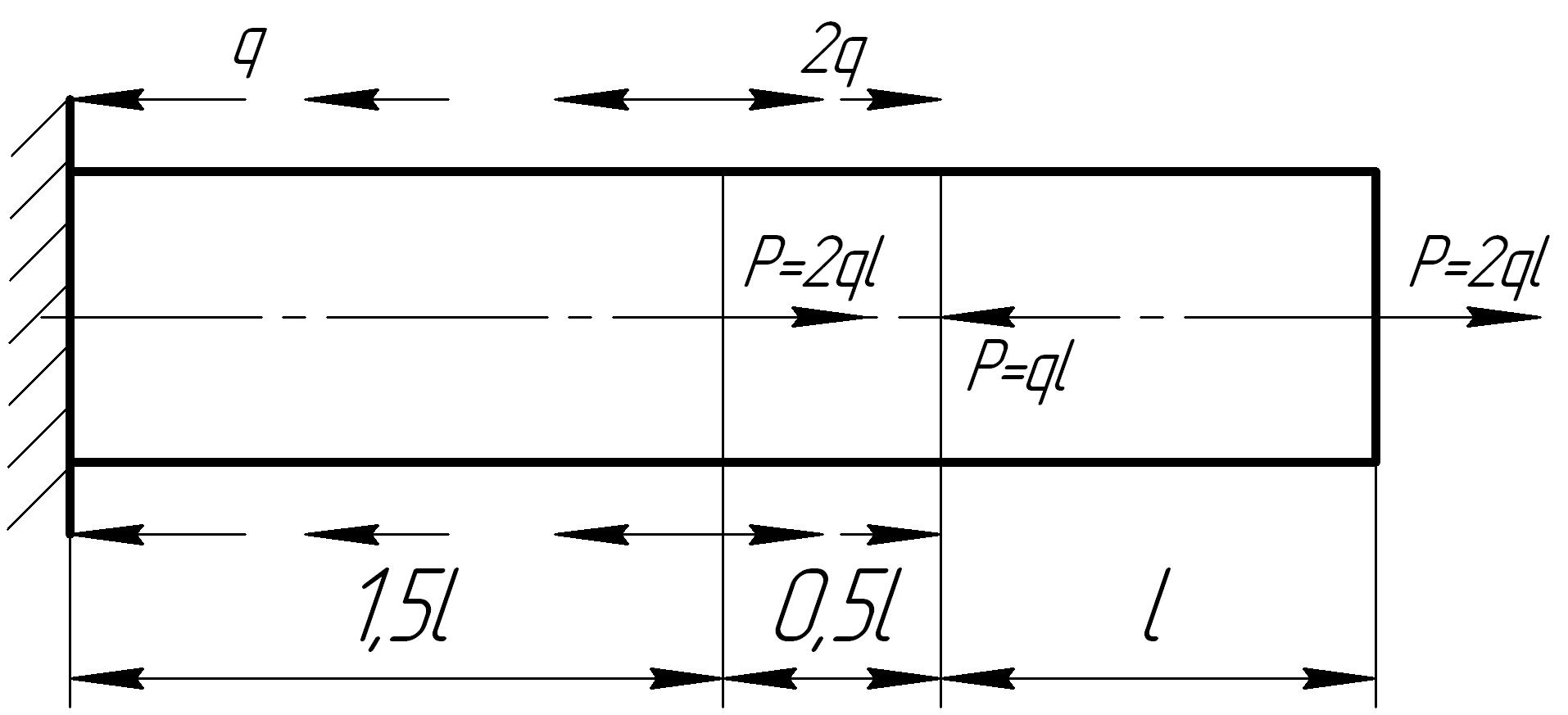
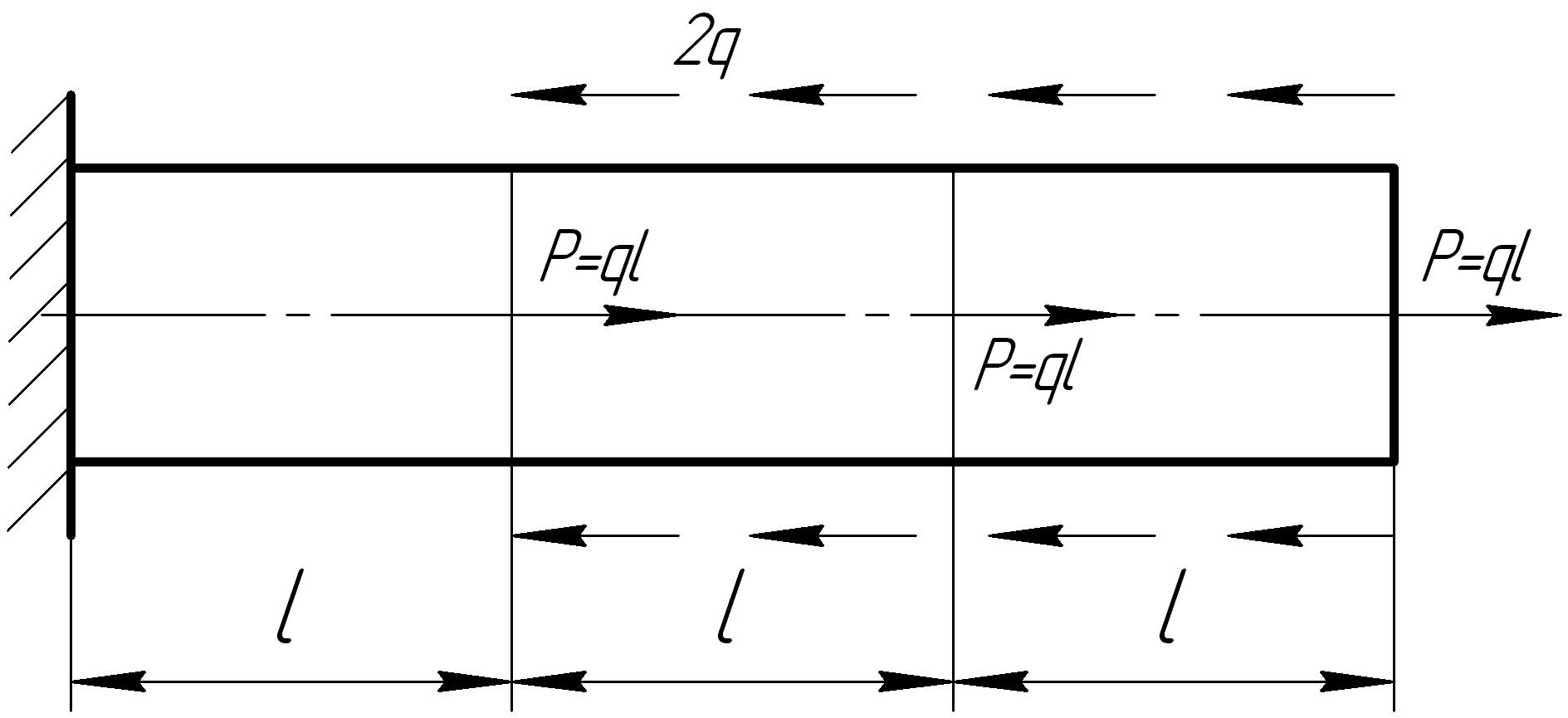
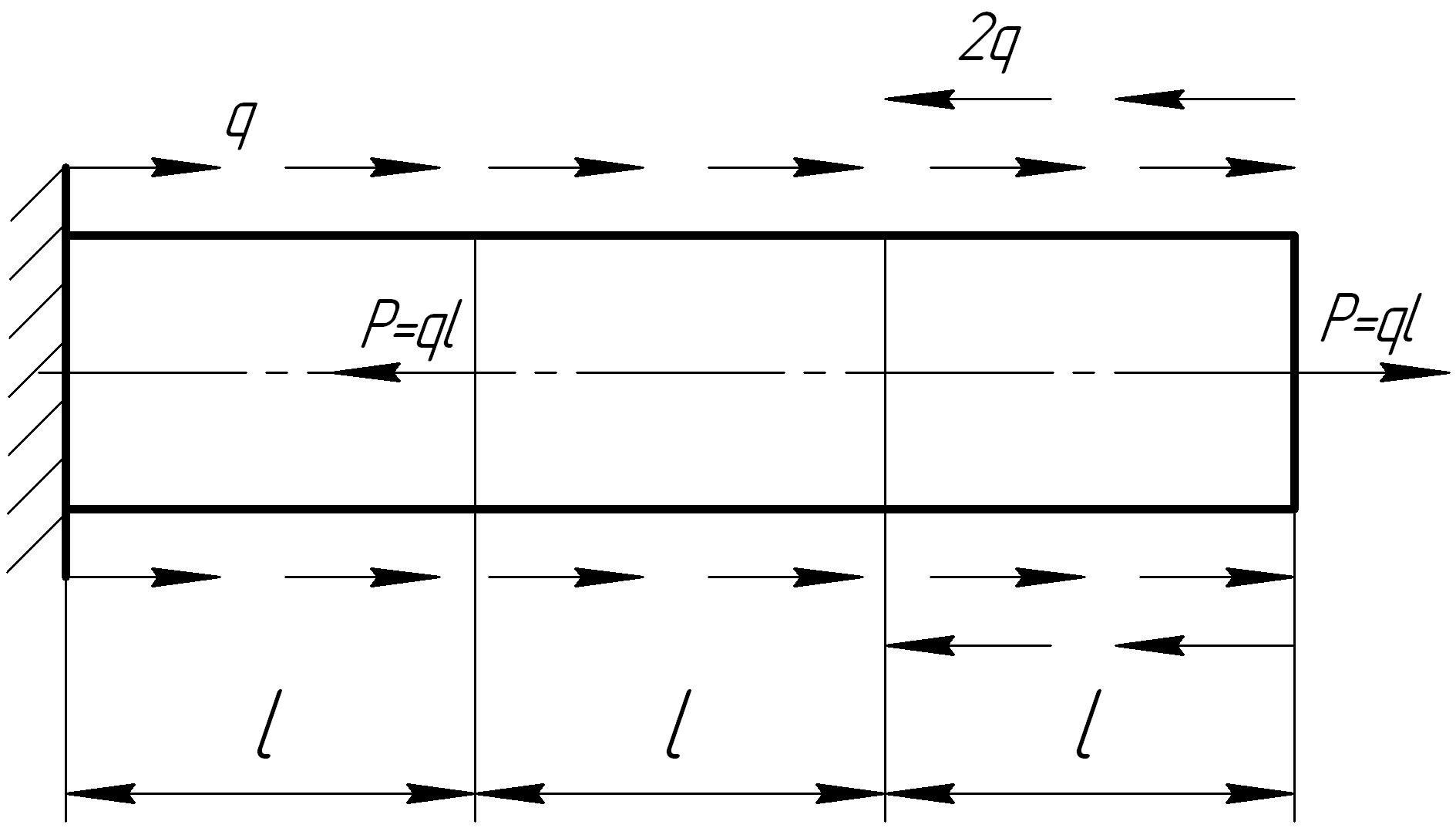
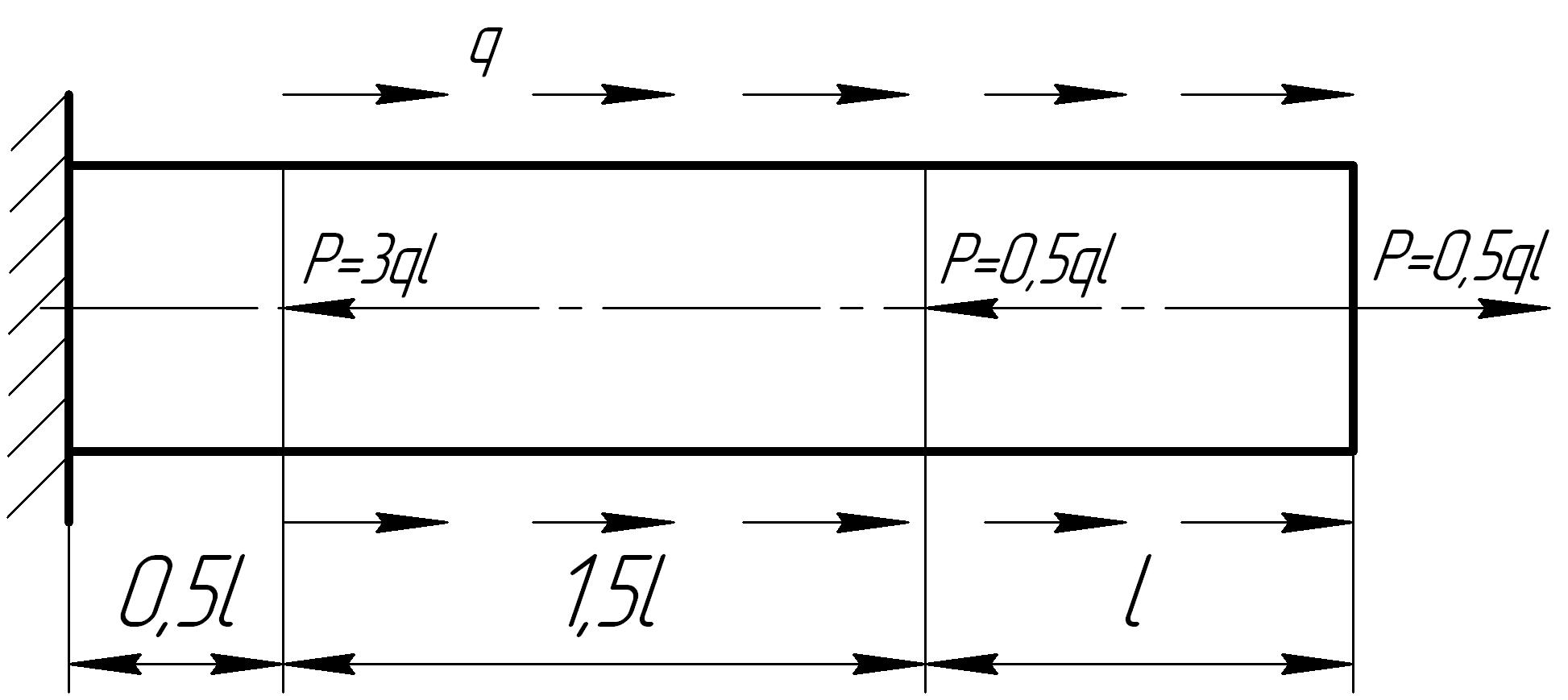
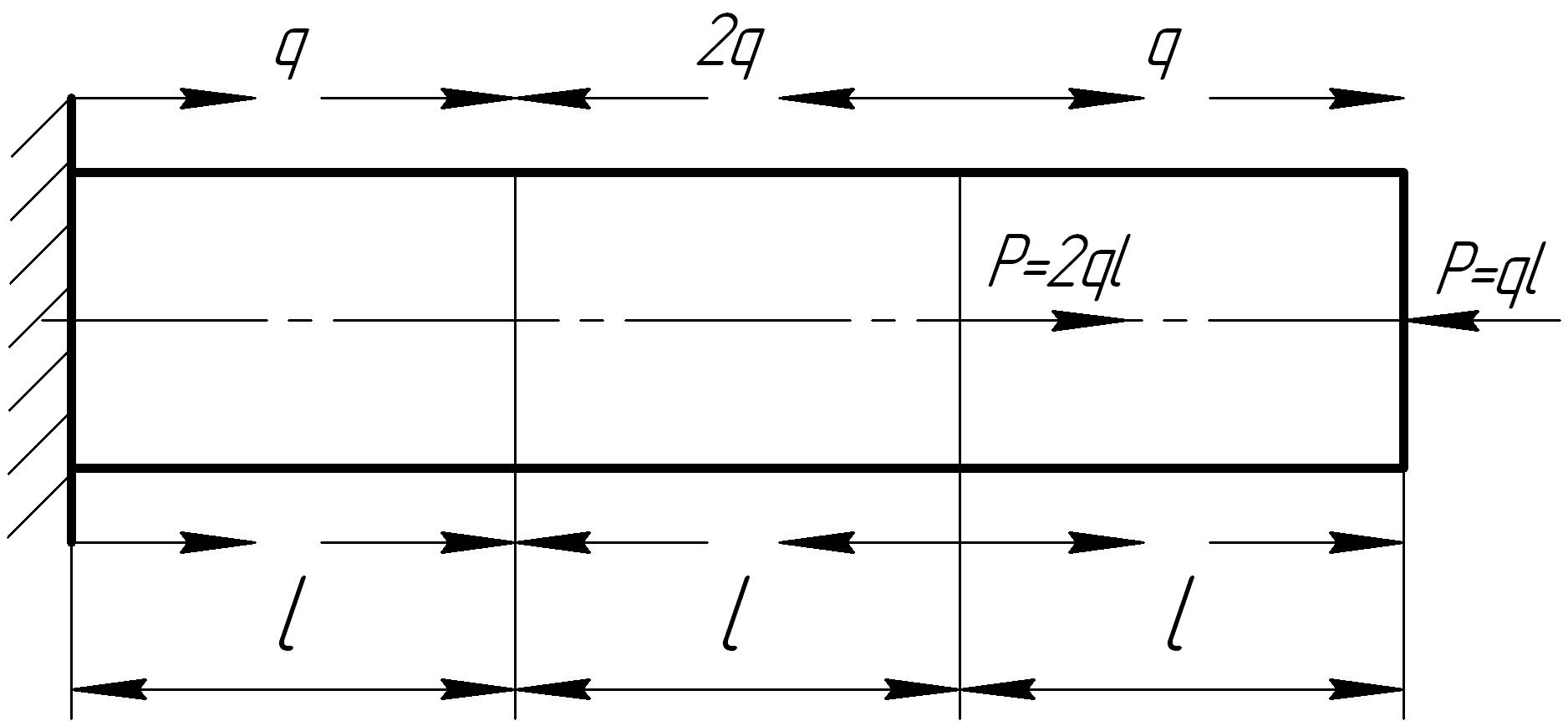
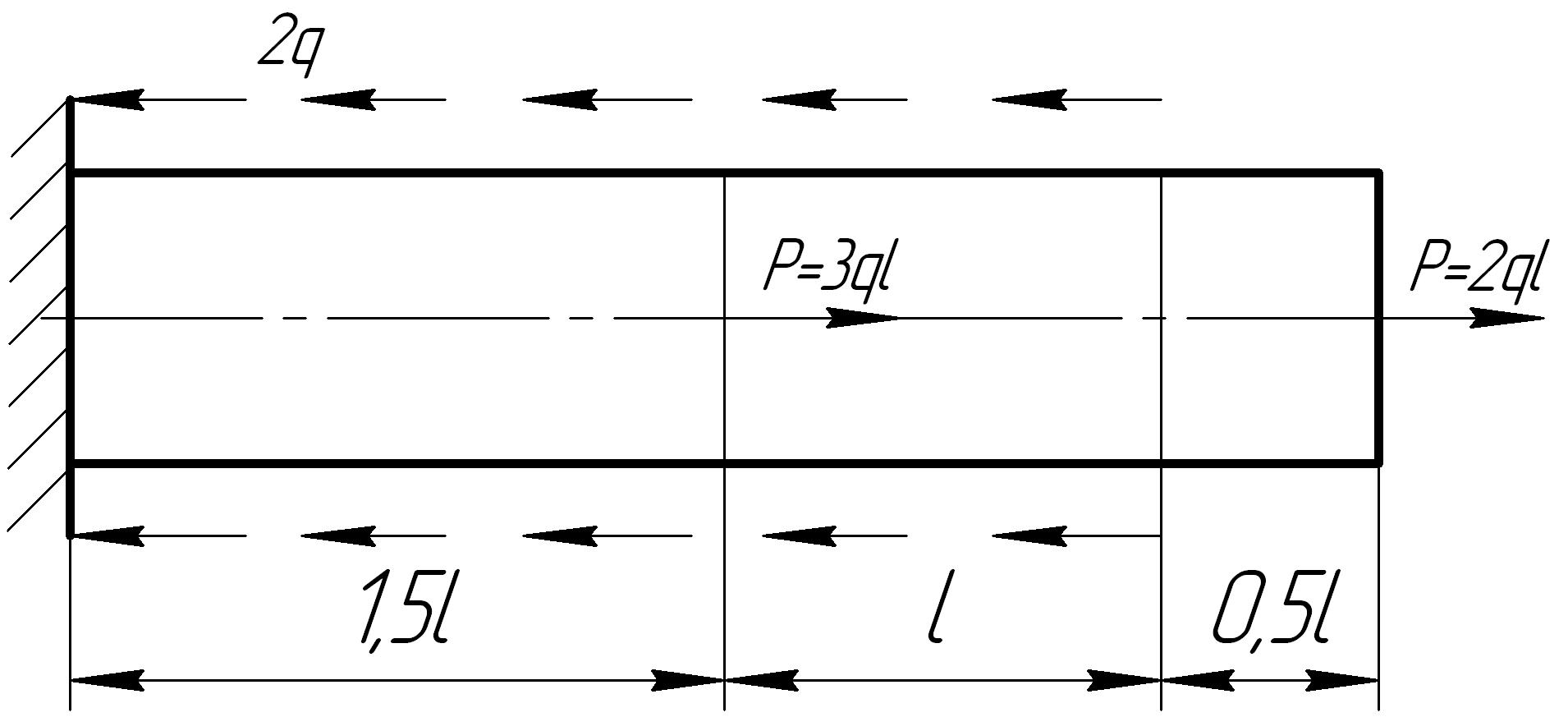
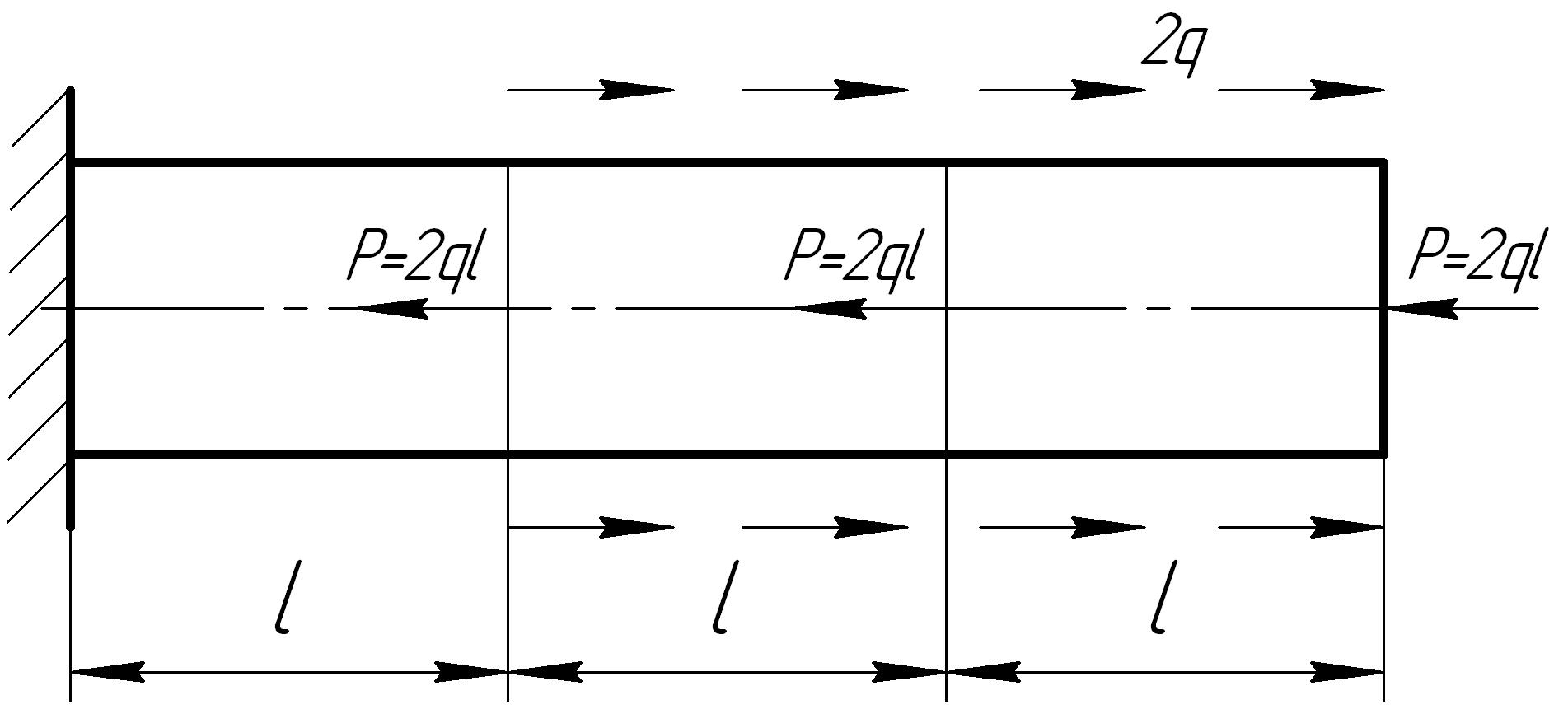
На основании исходных данных построить эпюру продольных сил
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
7. |
|
8. |
|
9. |
|
10. |
|
11. |
|
12. |
|
Рис. 6.6
13. |
|
14. |
|
15. |
|
16. |
|
17. |
|
18. |
|
19. |
|
20. |
|
21. |
|
22. |
|
23. |
|
24. |
|
Рис. 6.6
25. |
|
26. |
|
27. |
|
28. |
|
29. |
|
30. |
|
Рис. 6.6
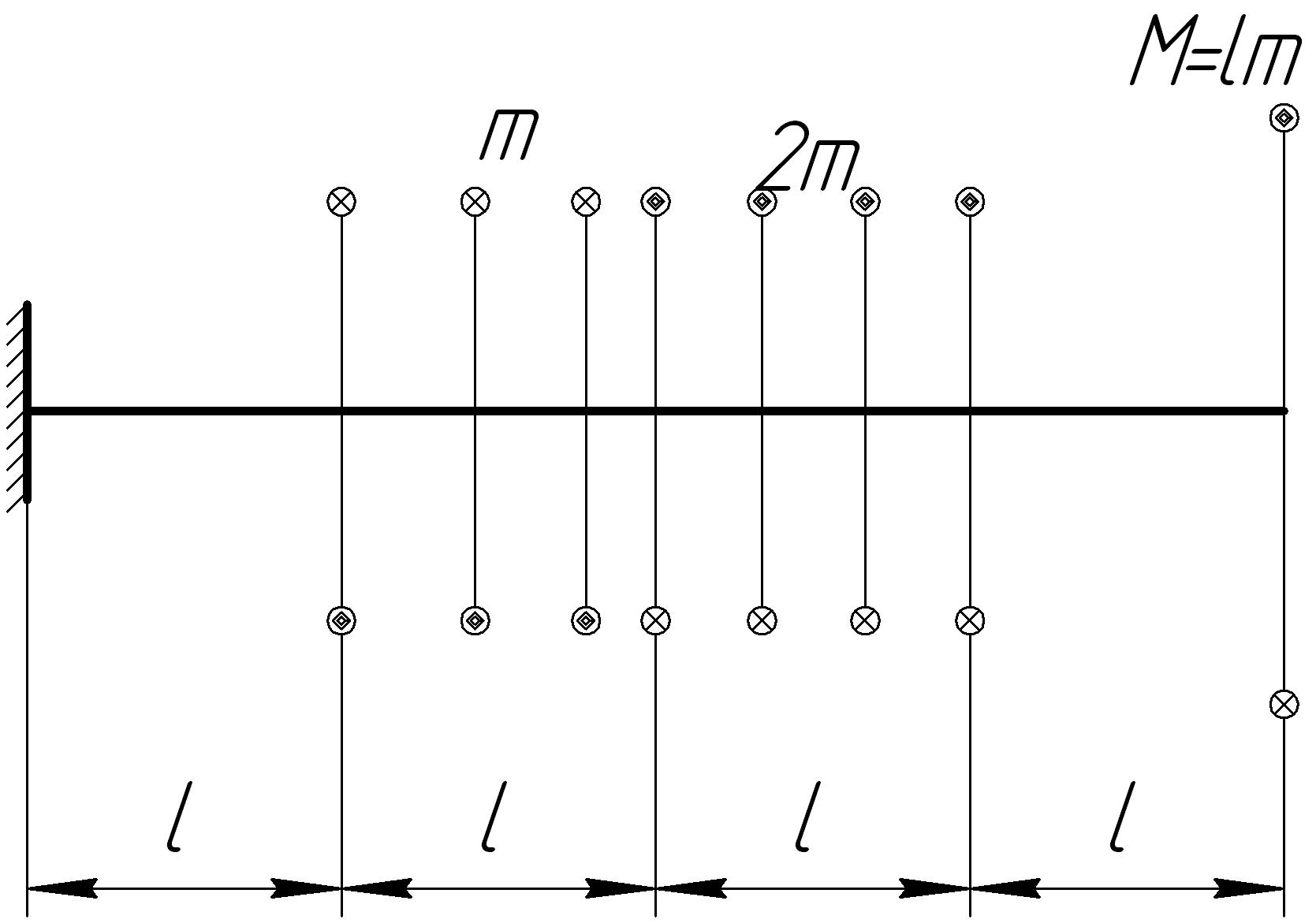
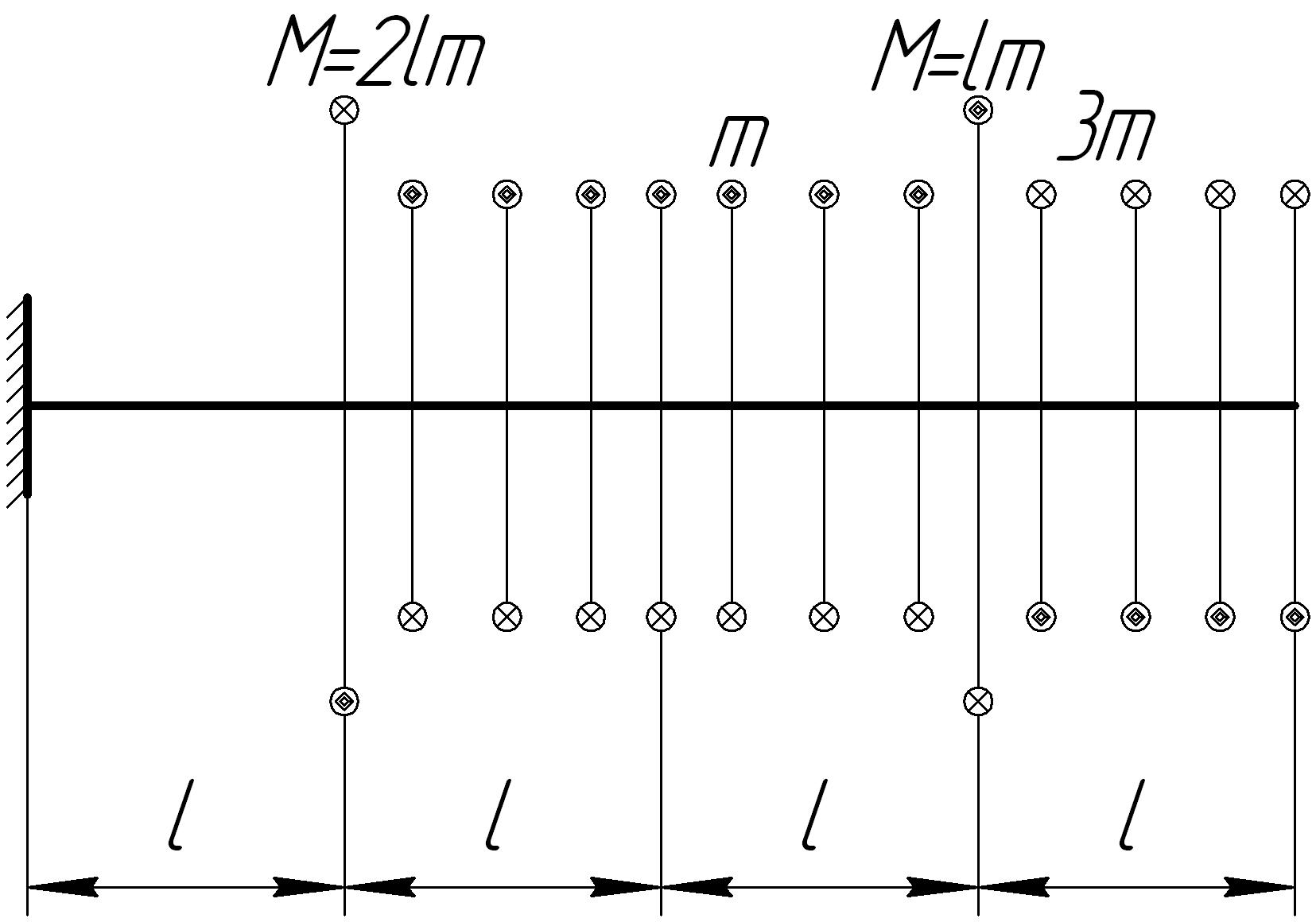
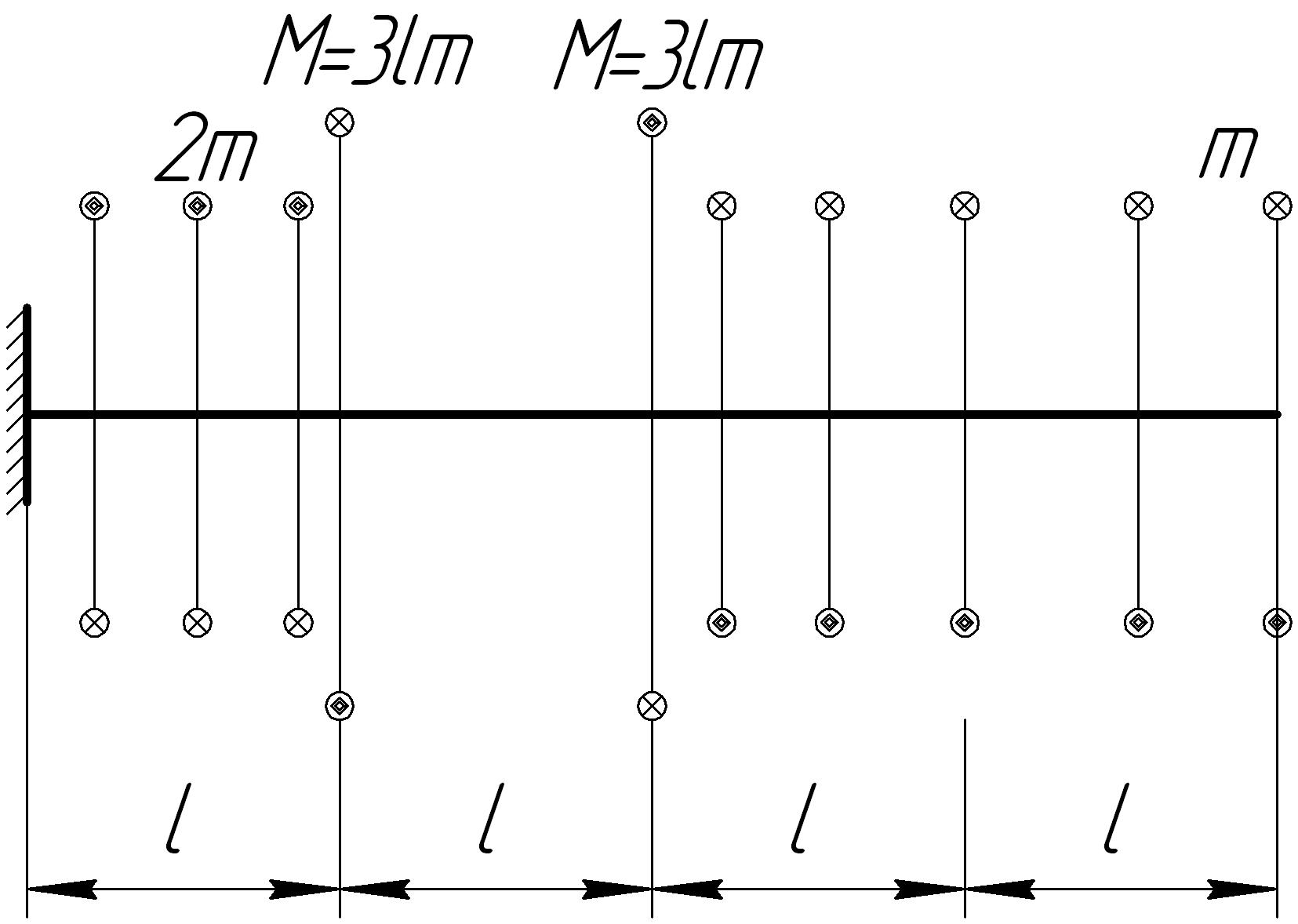
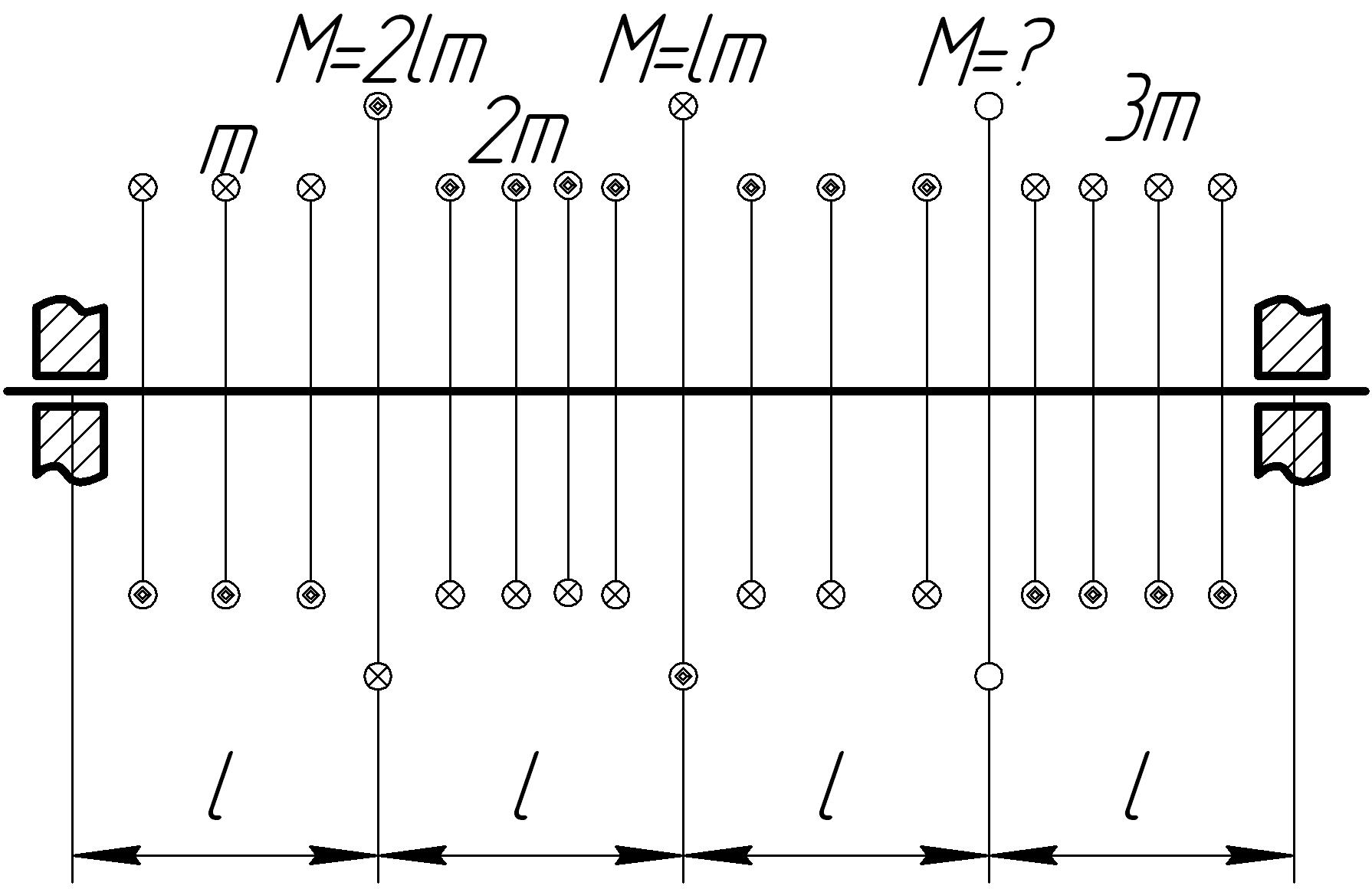
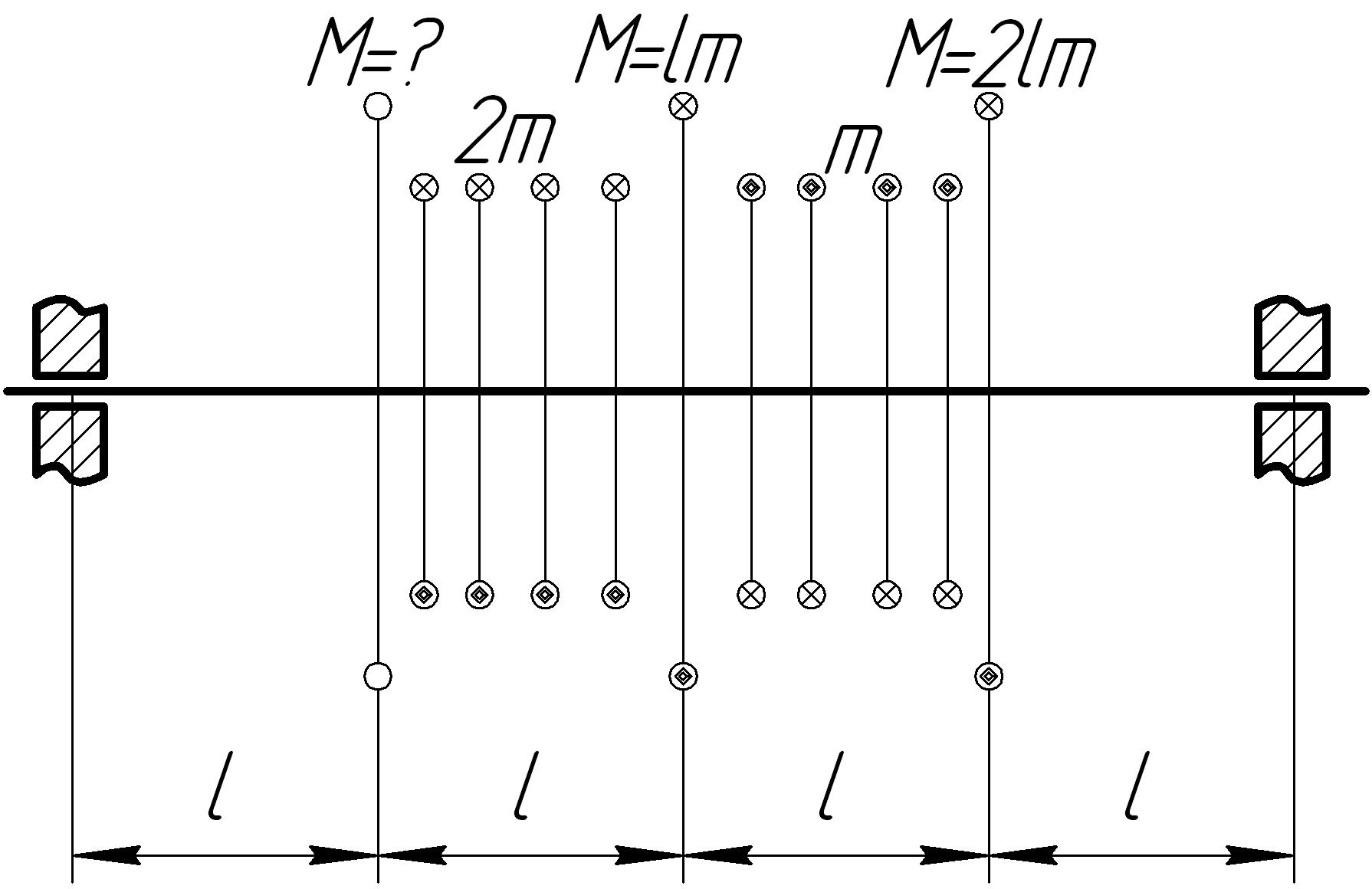
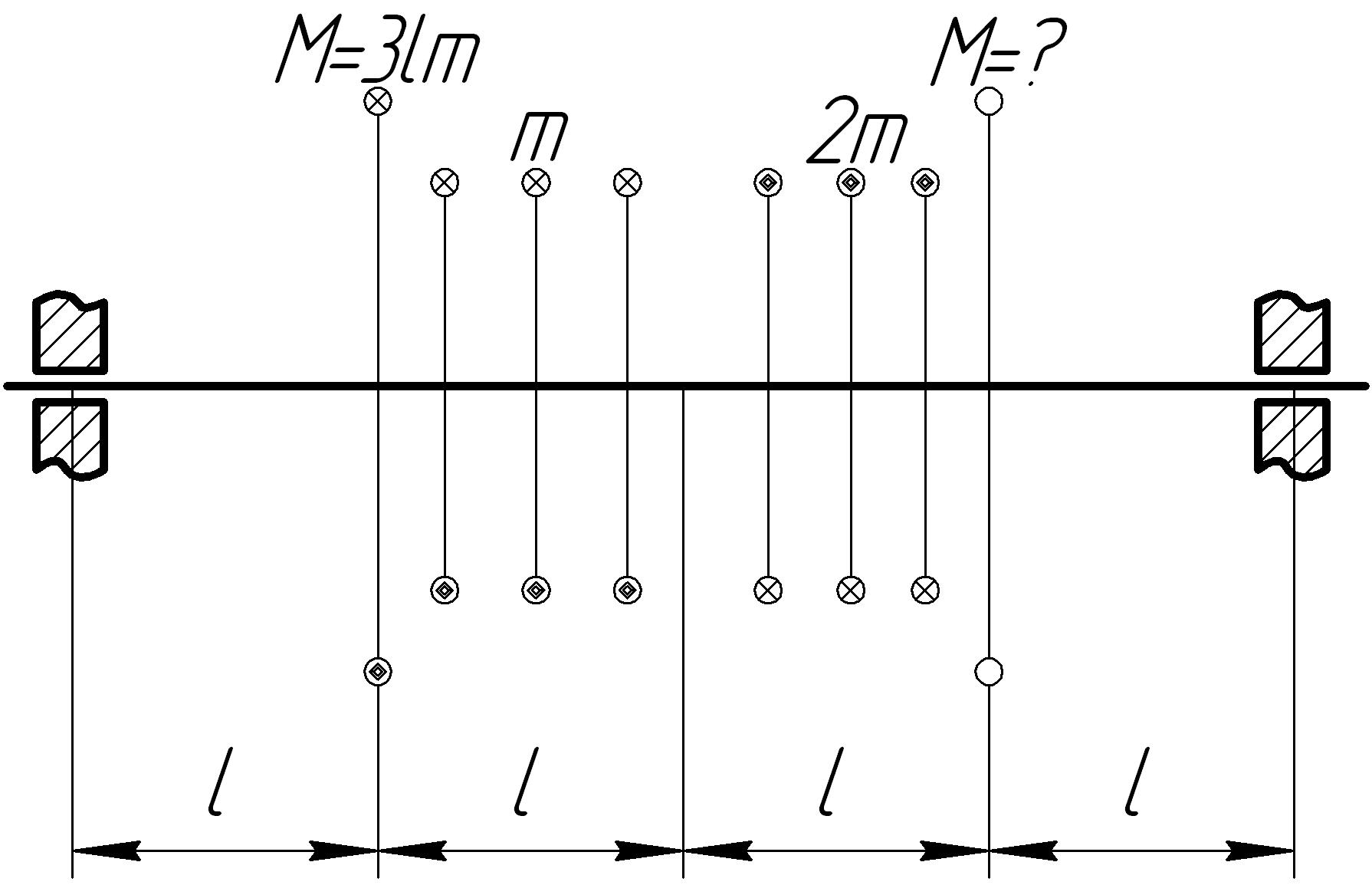
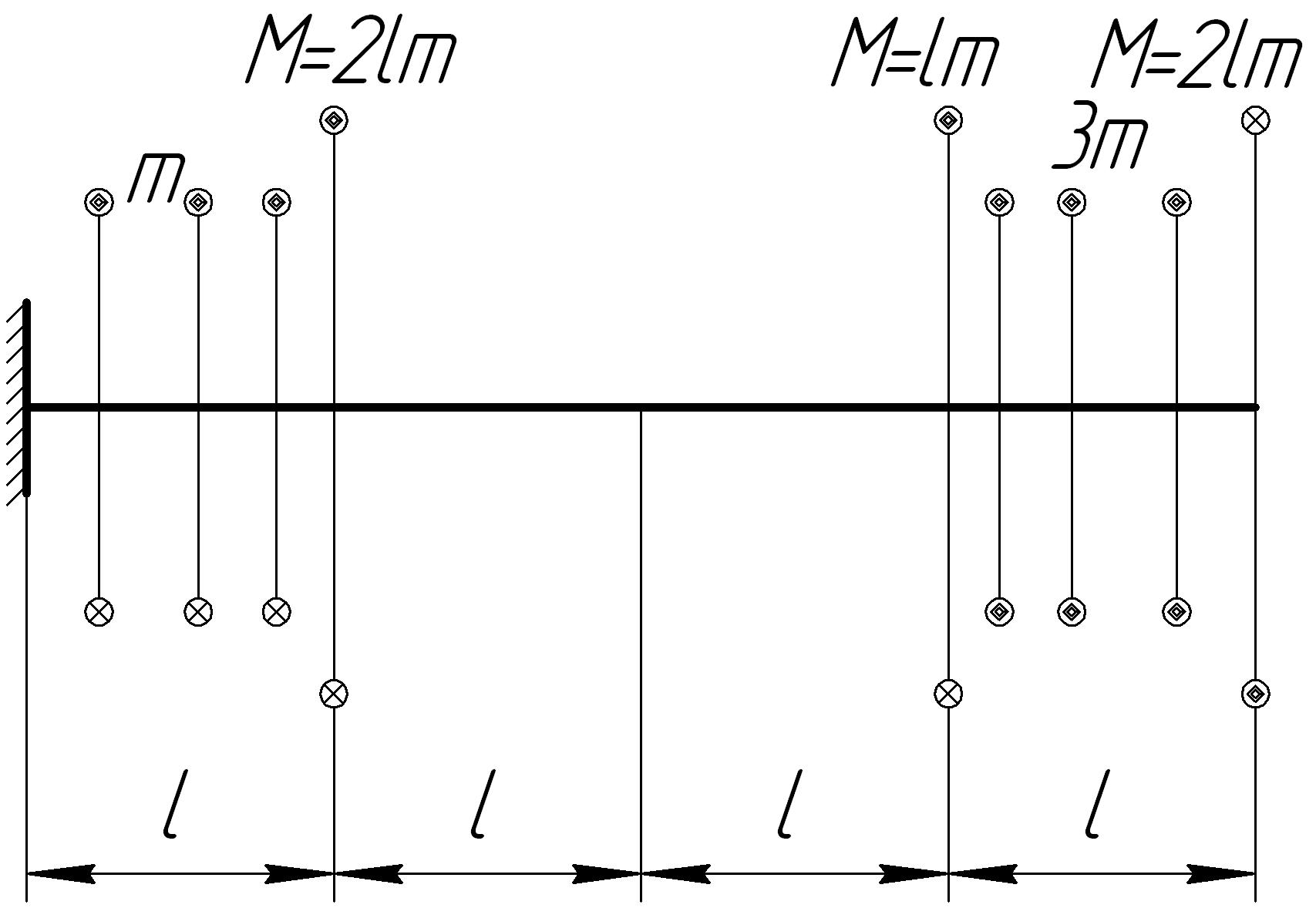
Задача 7
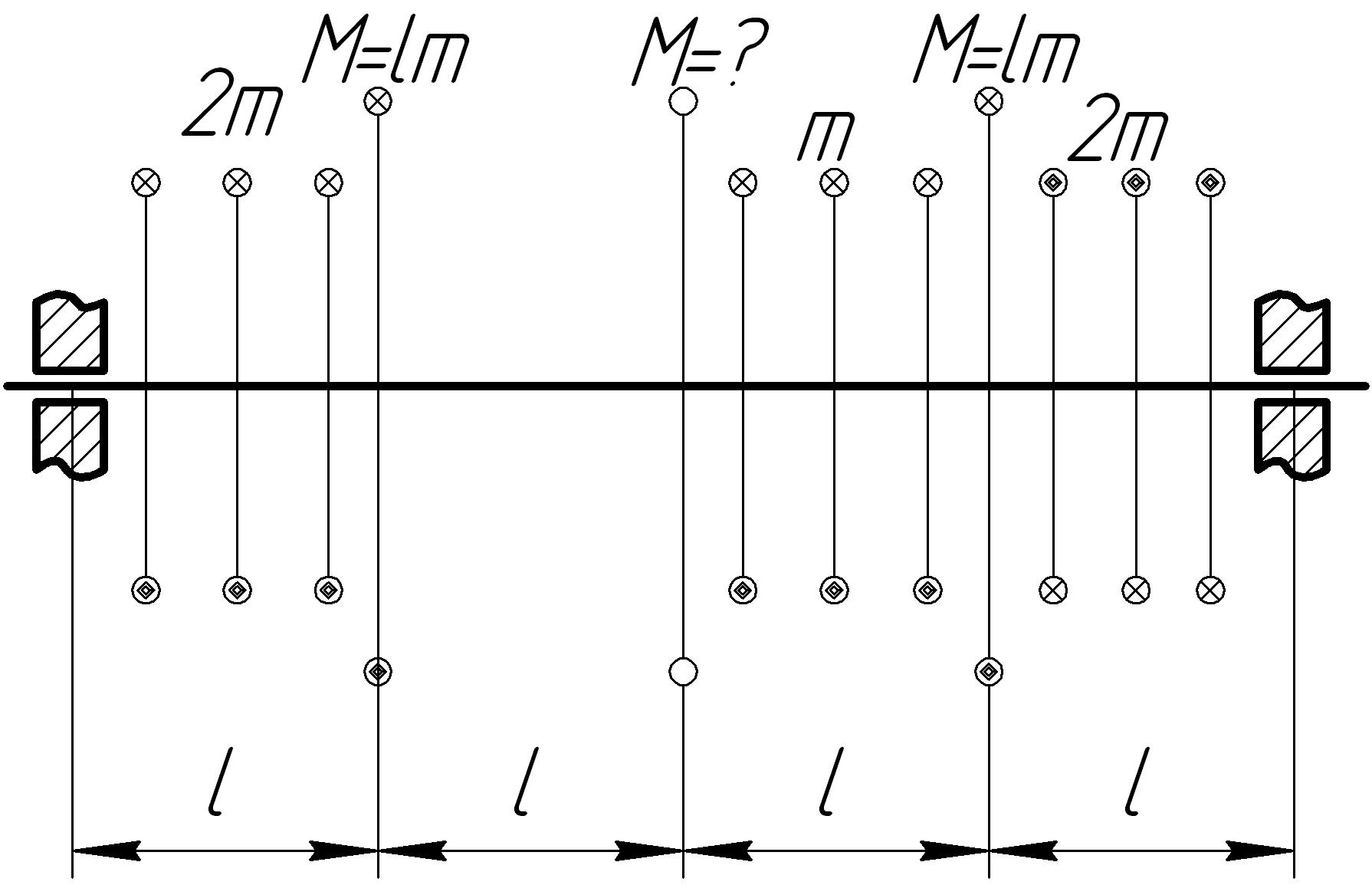
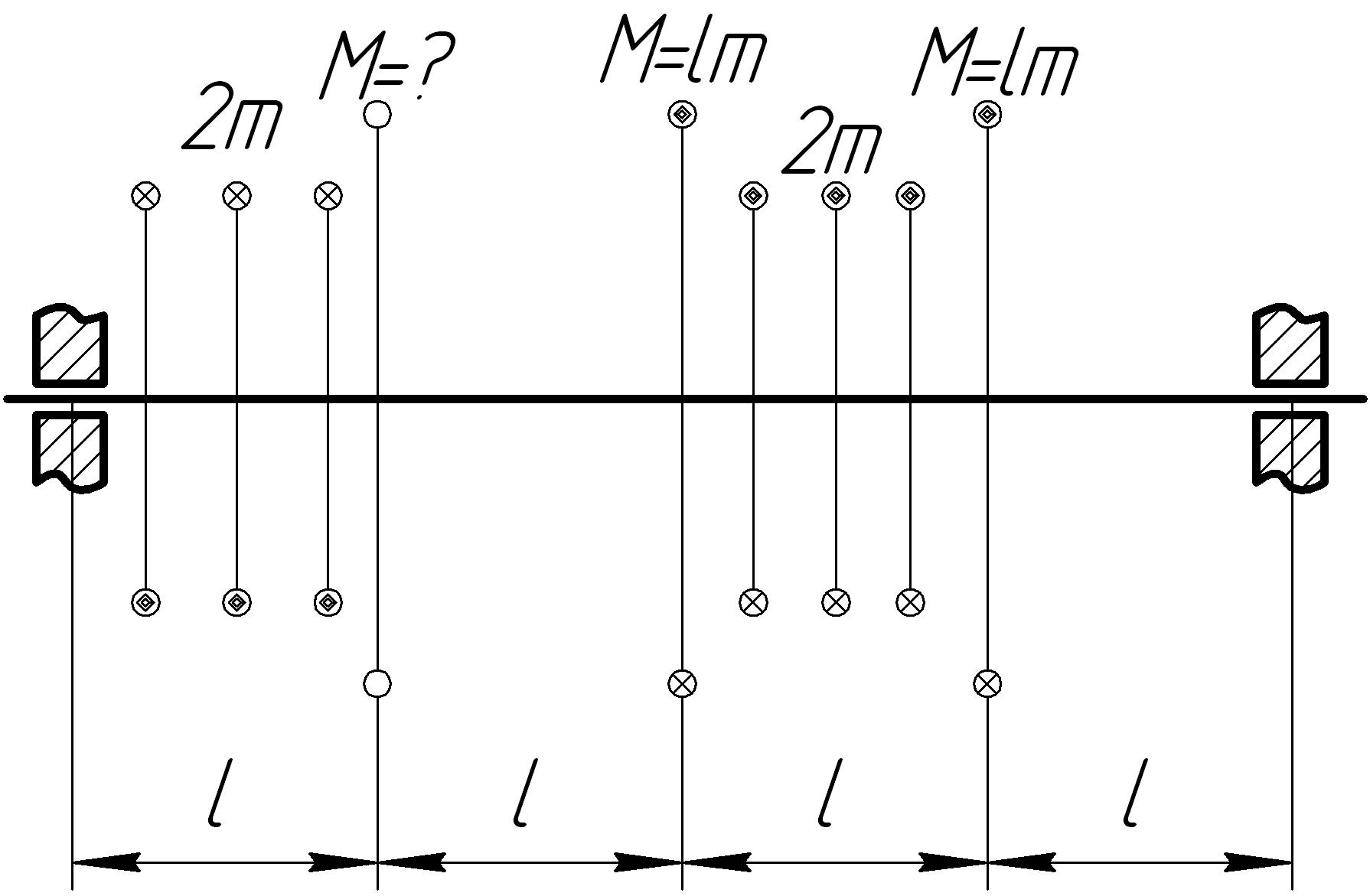
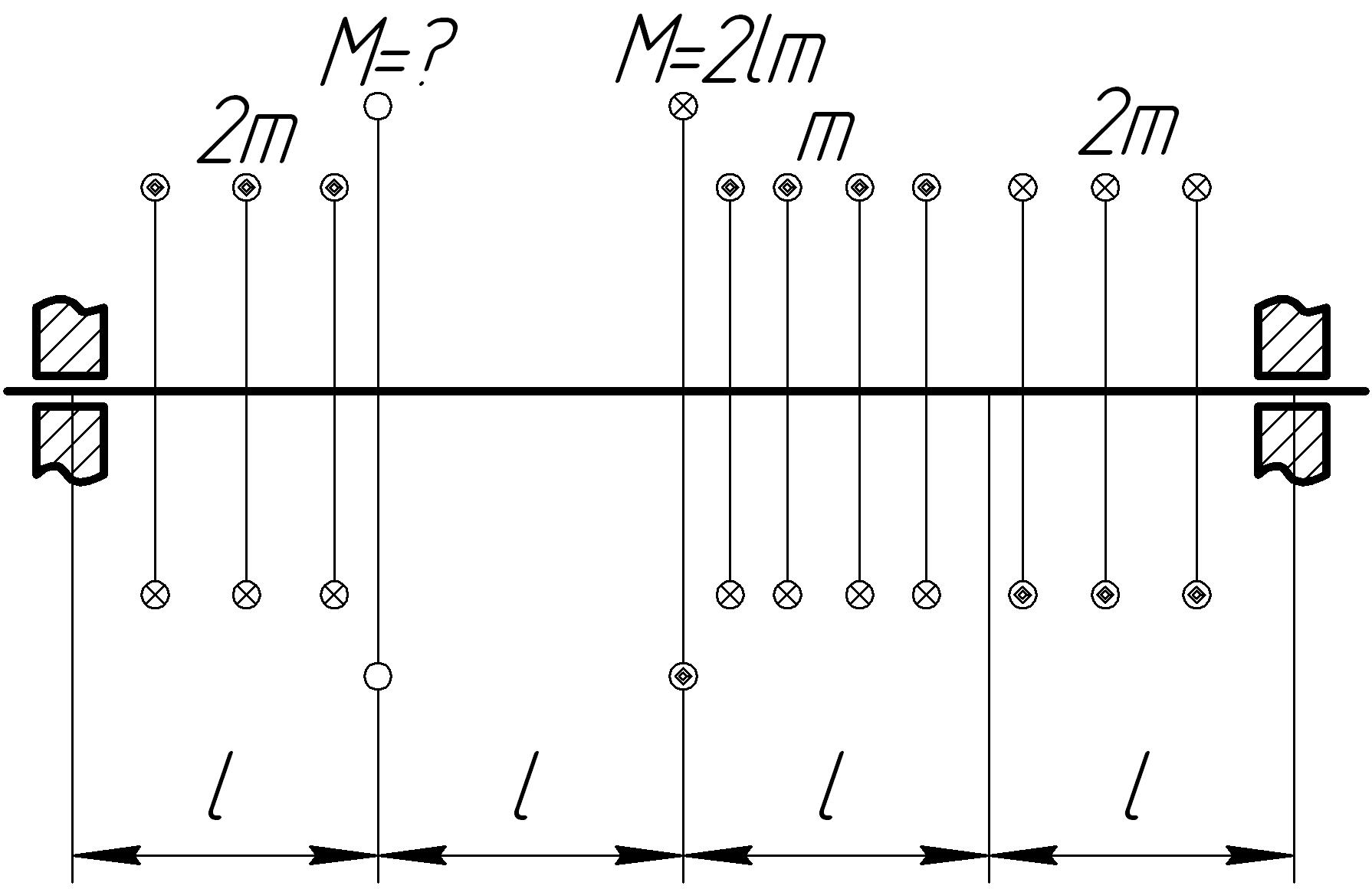
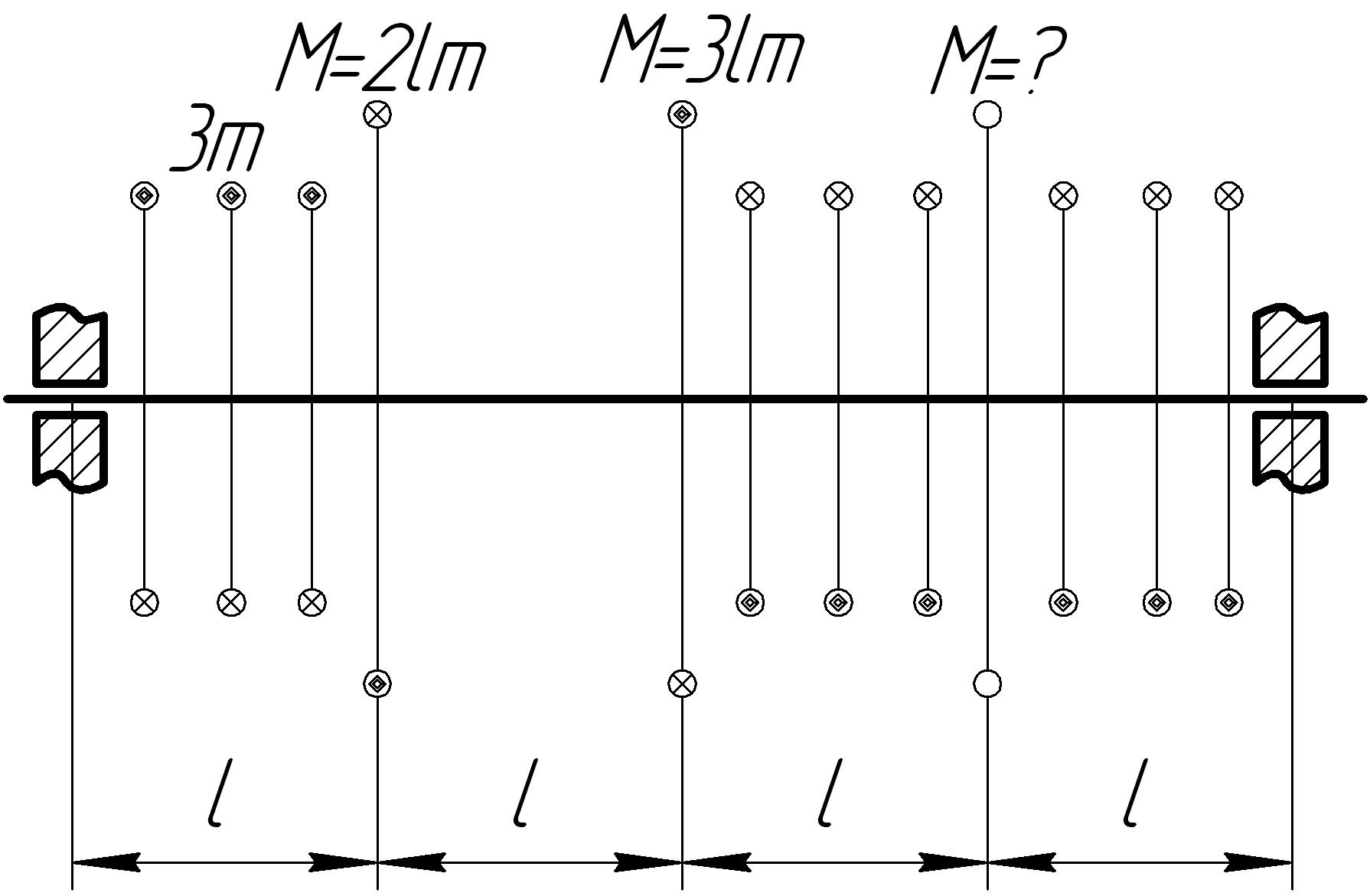
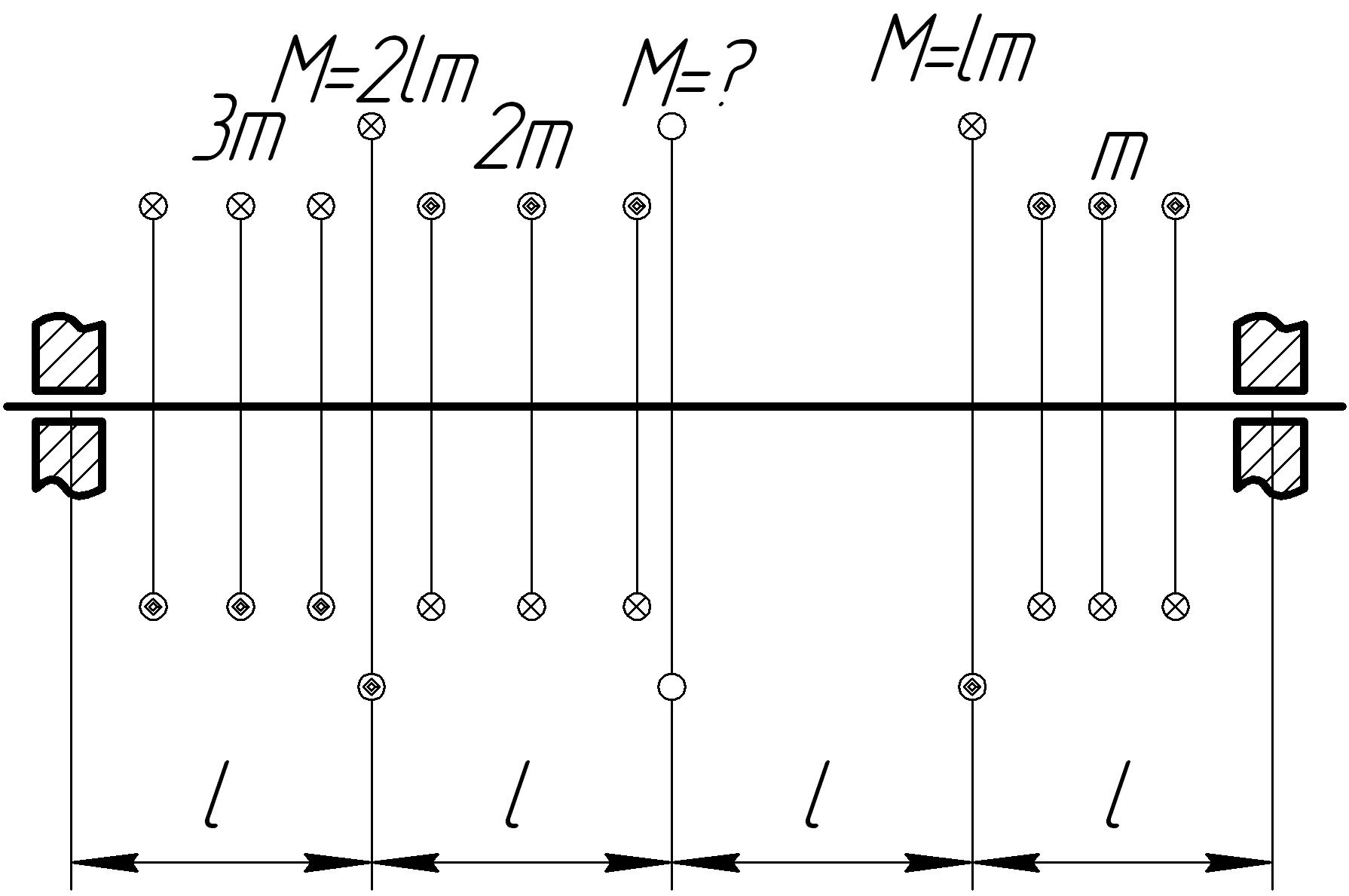
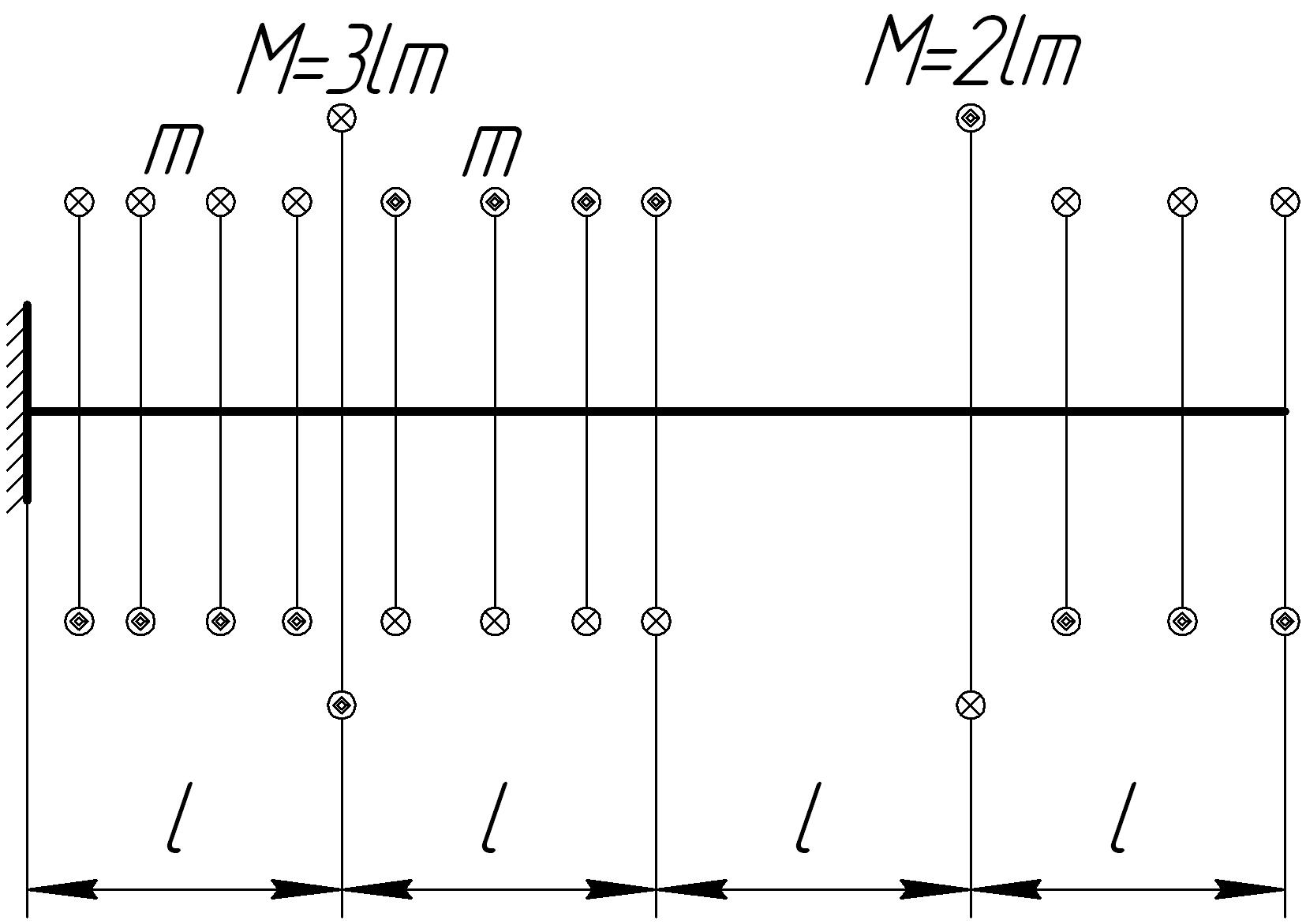
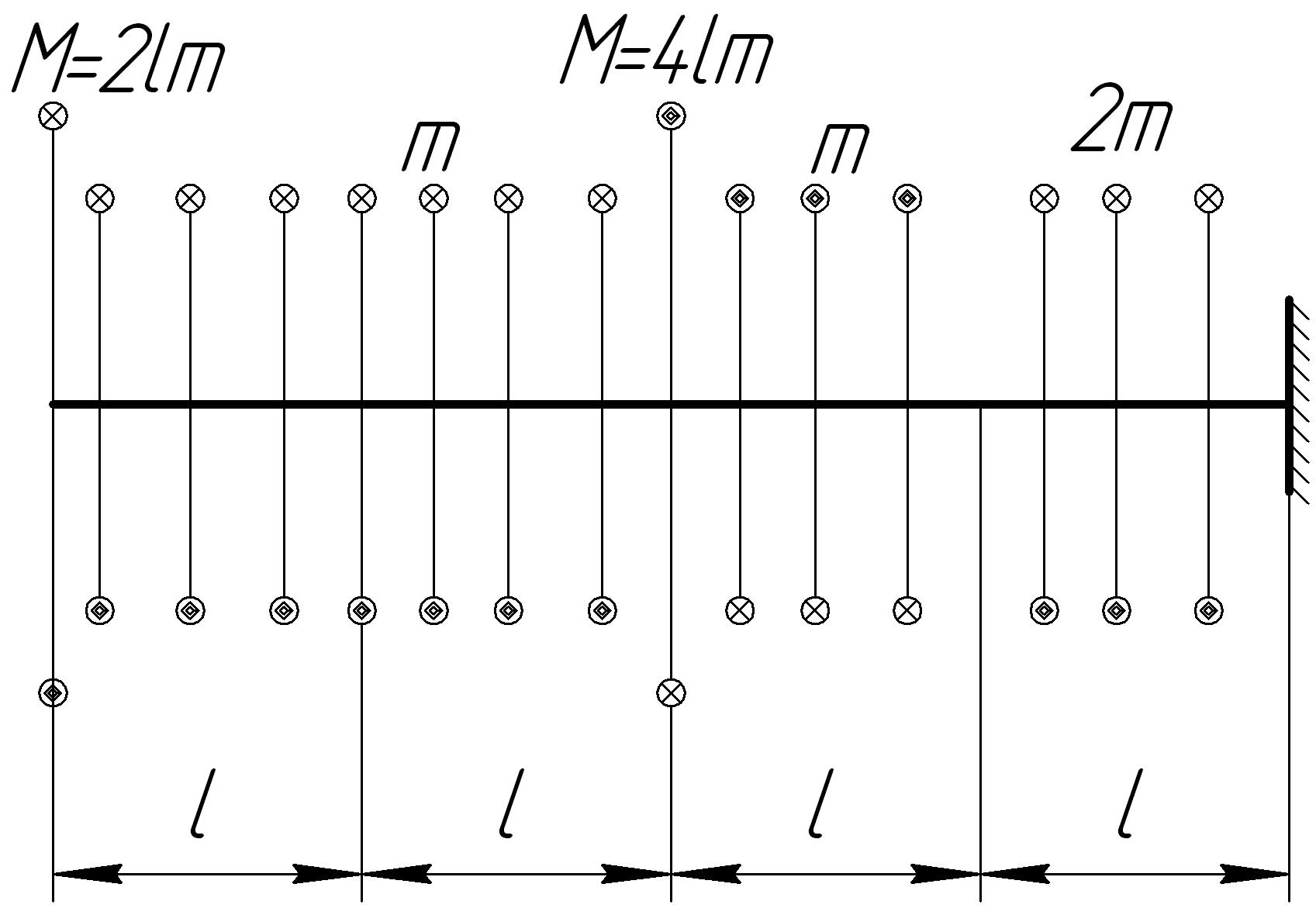
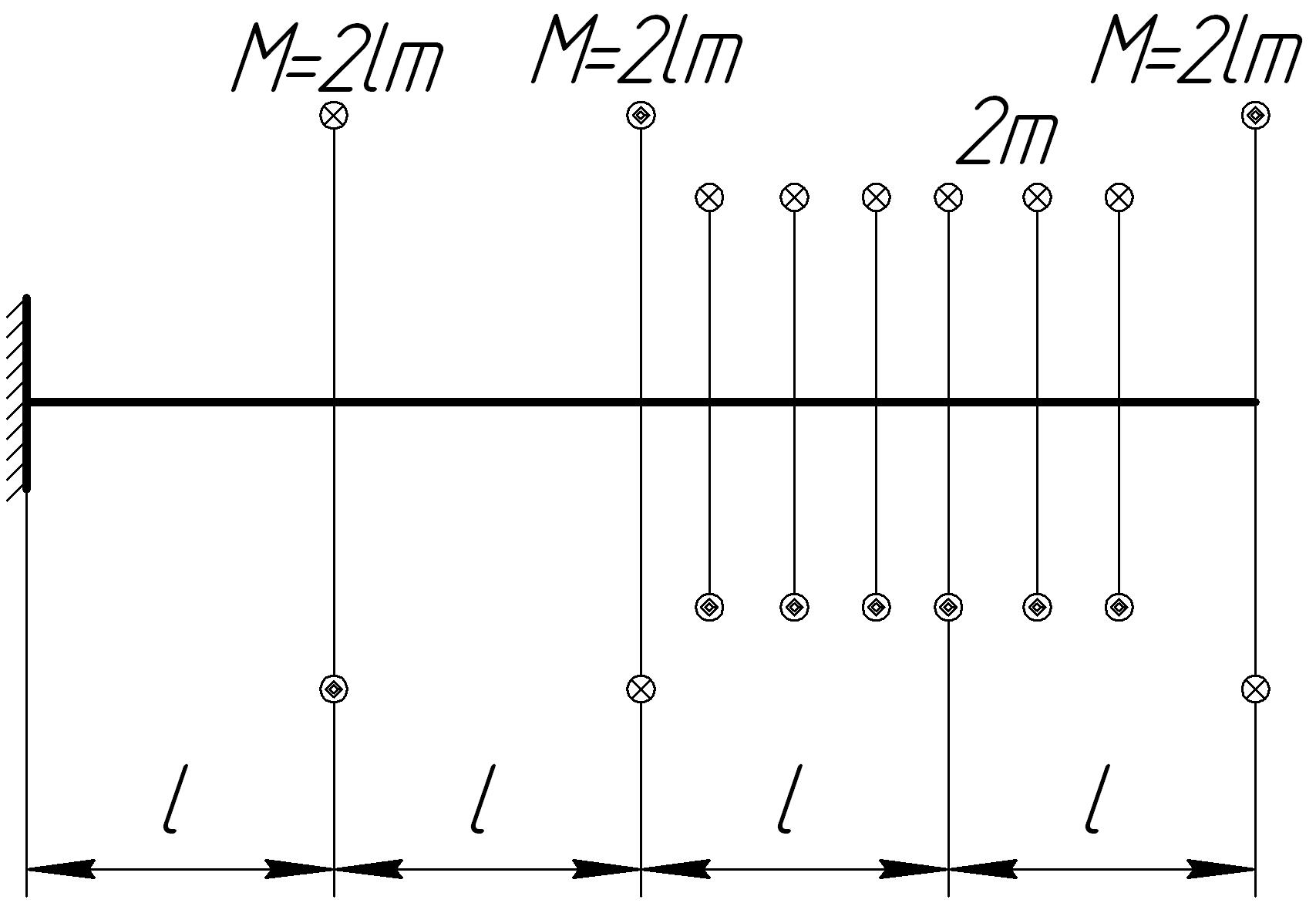
На основании исходных данных (рис. 6.7) построить эпюру внутренних силовых факторов при кручении.
1. |
|
2. |
|
Рис. 6.7
3. |
|
4. |
|
5. |
|
6. |
|
7. |
|
8. |
|
9. |
|
10. |
|
Рис. 6.7
11. |
|
12. |
|
13. |
|
14. |
|
15. |
|
16. |
|
17. |
|
18. |
|
Рис. 6.7
19. |
|
20. |
|
21. |
|
22. |
|
23. |
|
24. |
|
25. |
|
26. |
|
Рис. 6.7
27. |
|
28. |
|
29. |
|
30. |
|
Рис. 6.7
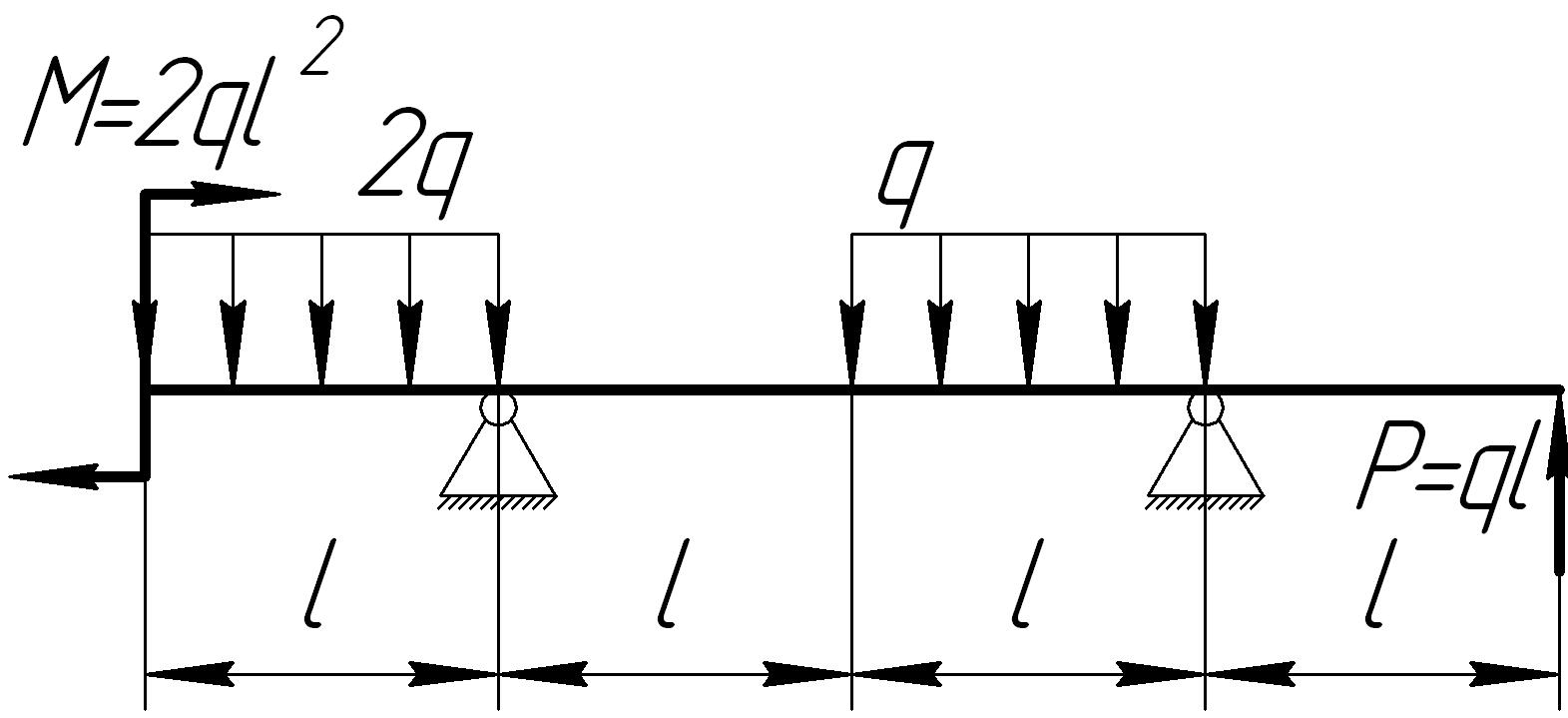
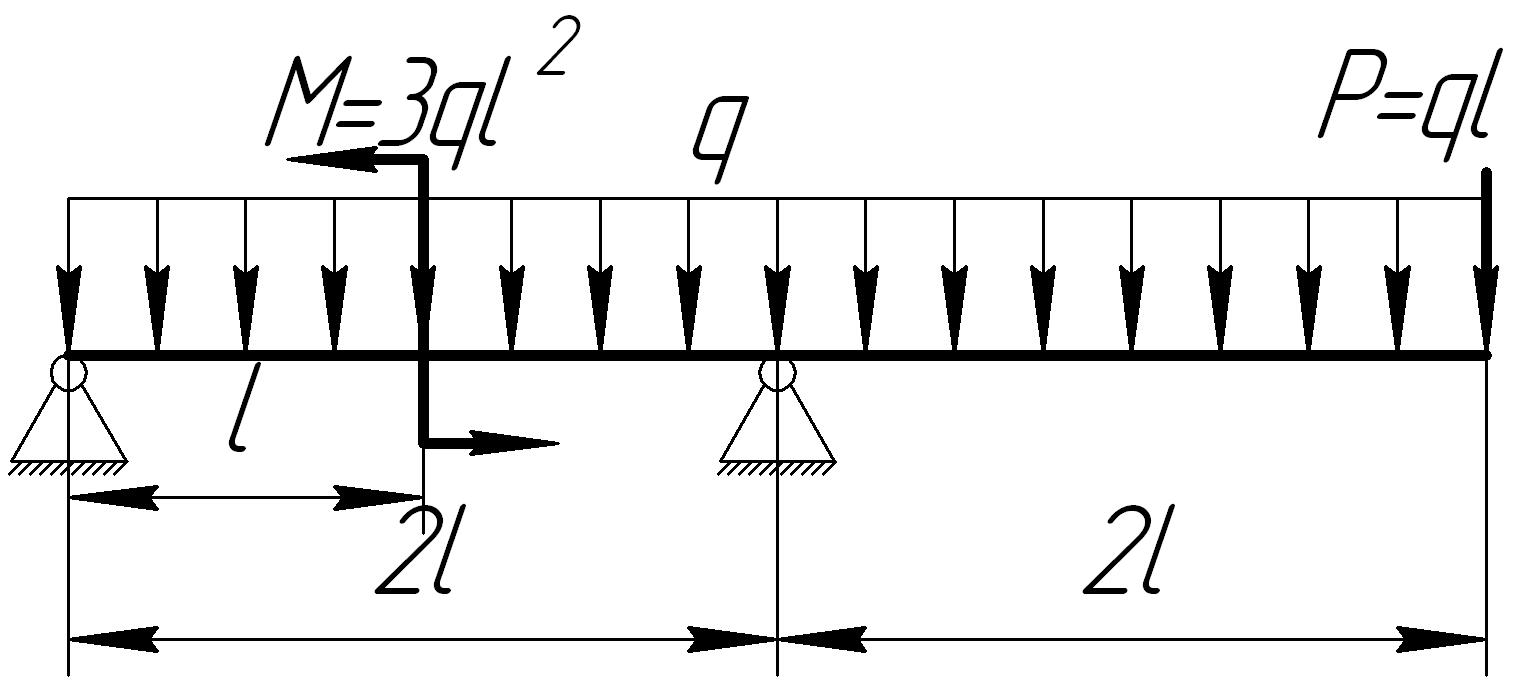
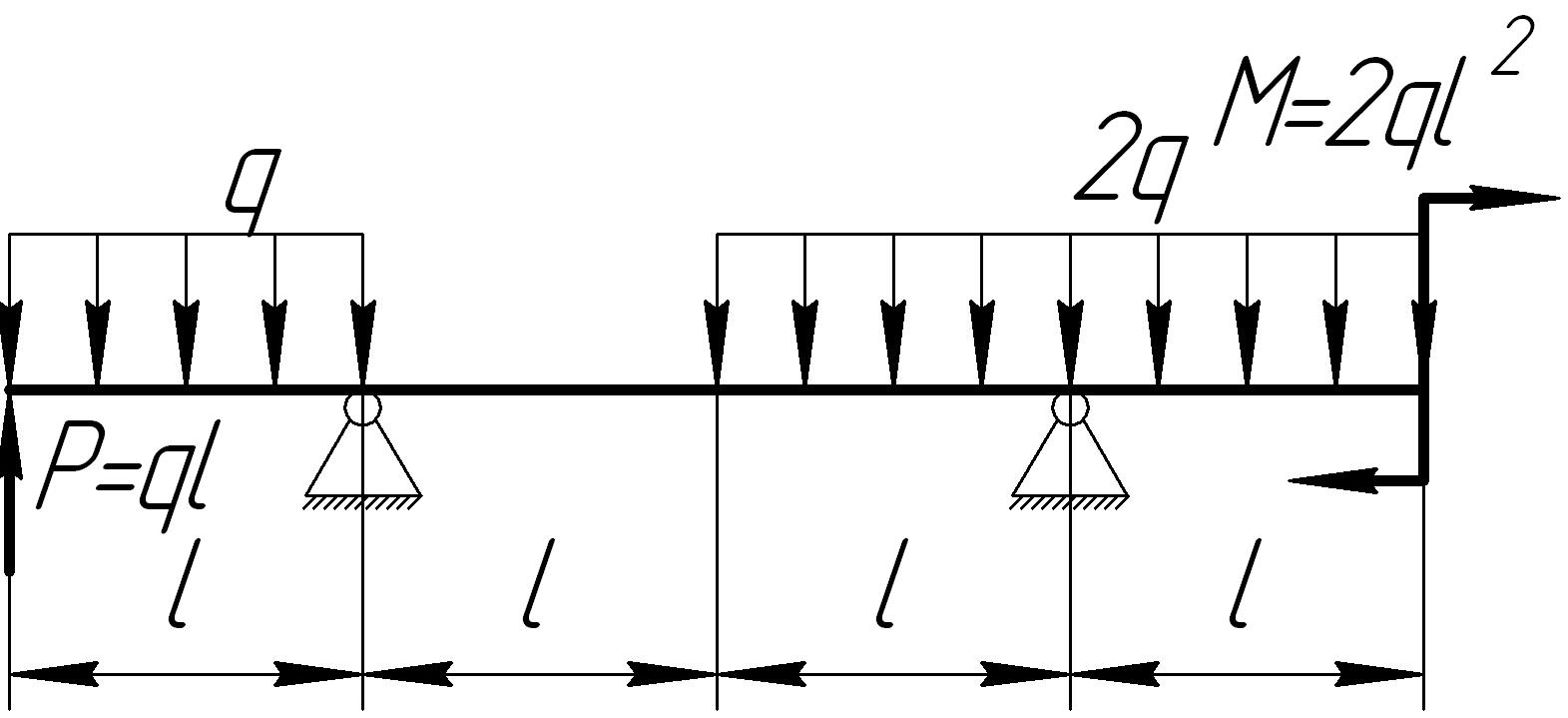
Задача 8
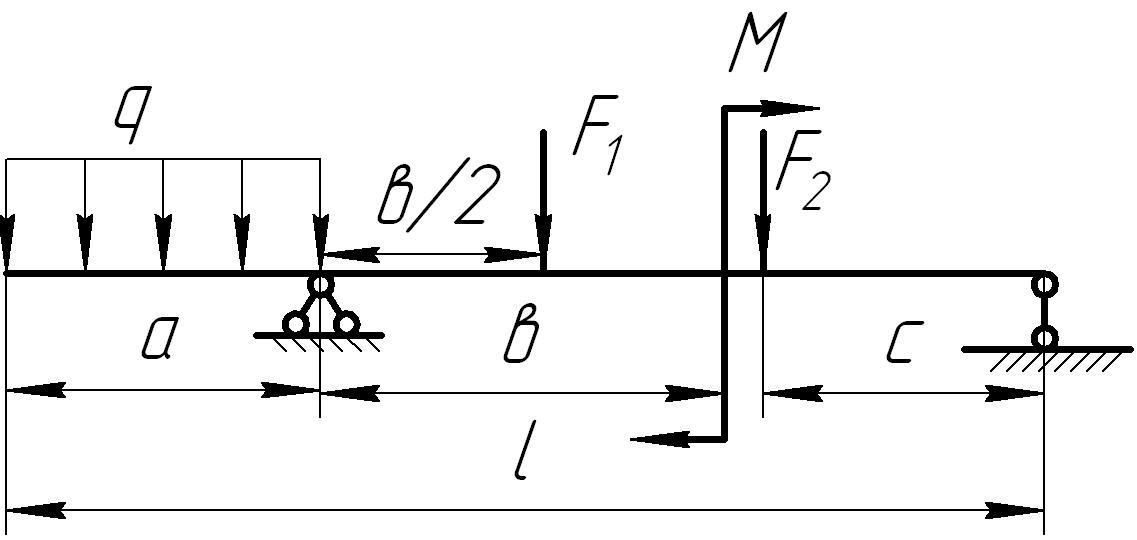
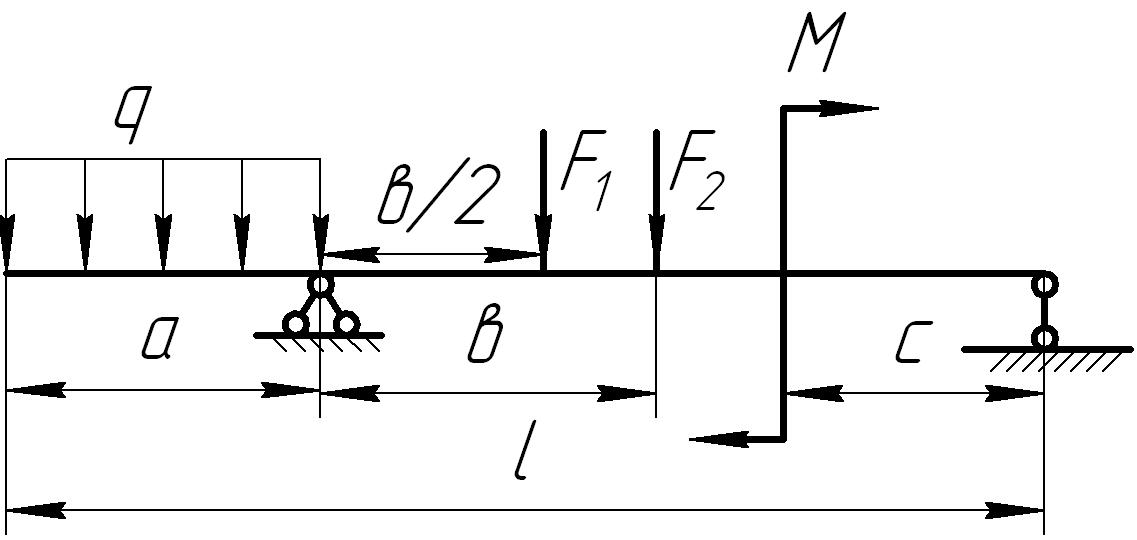
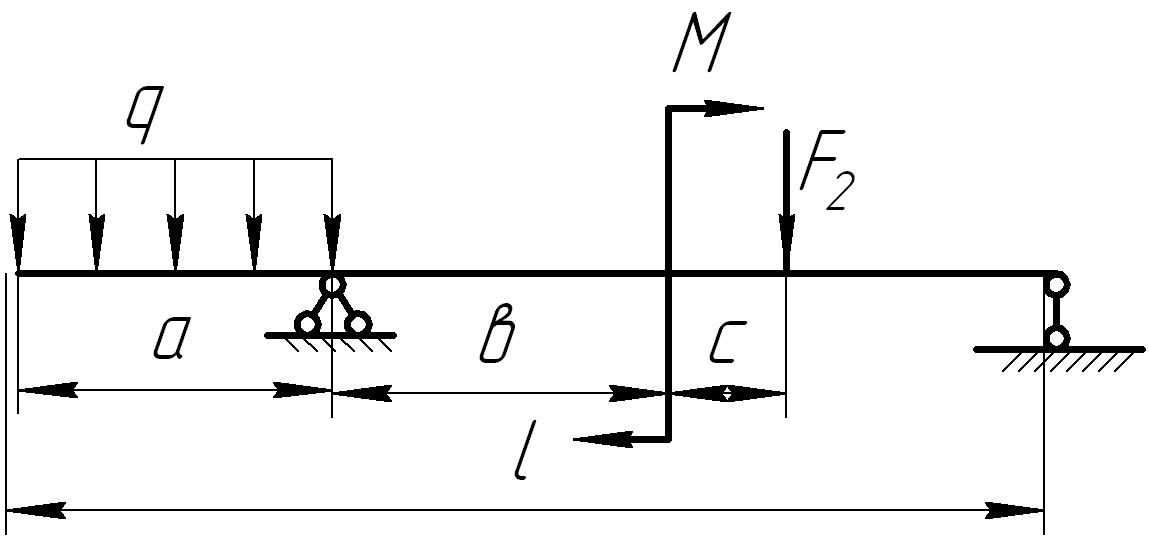
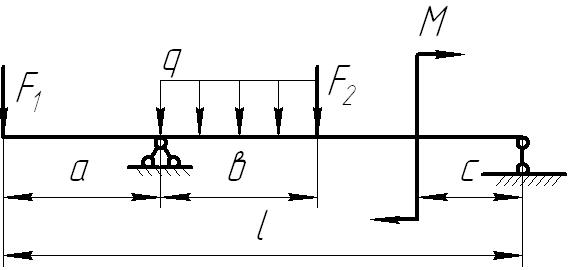
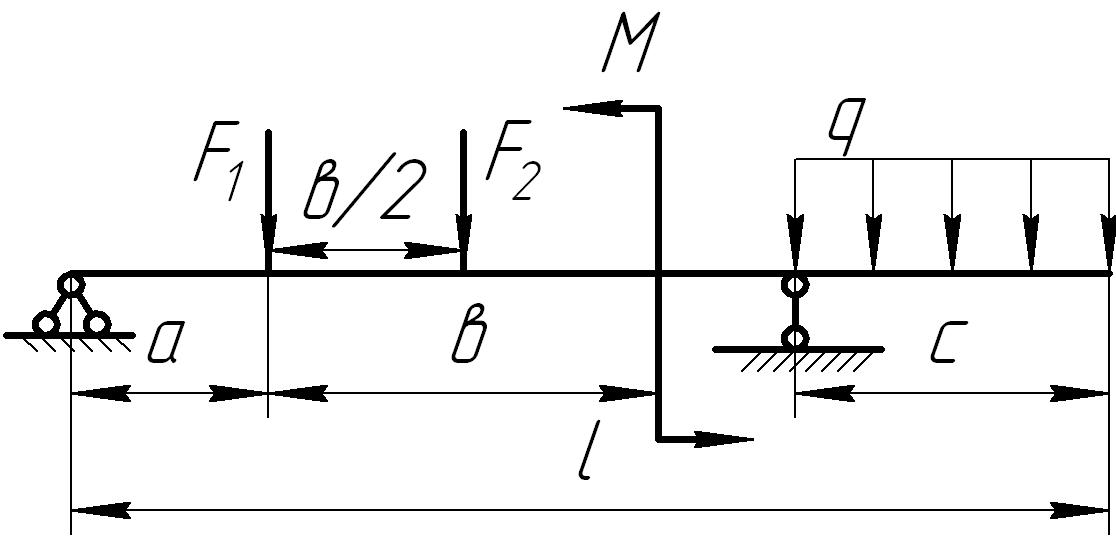
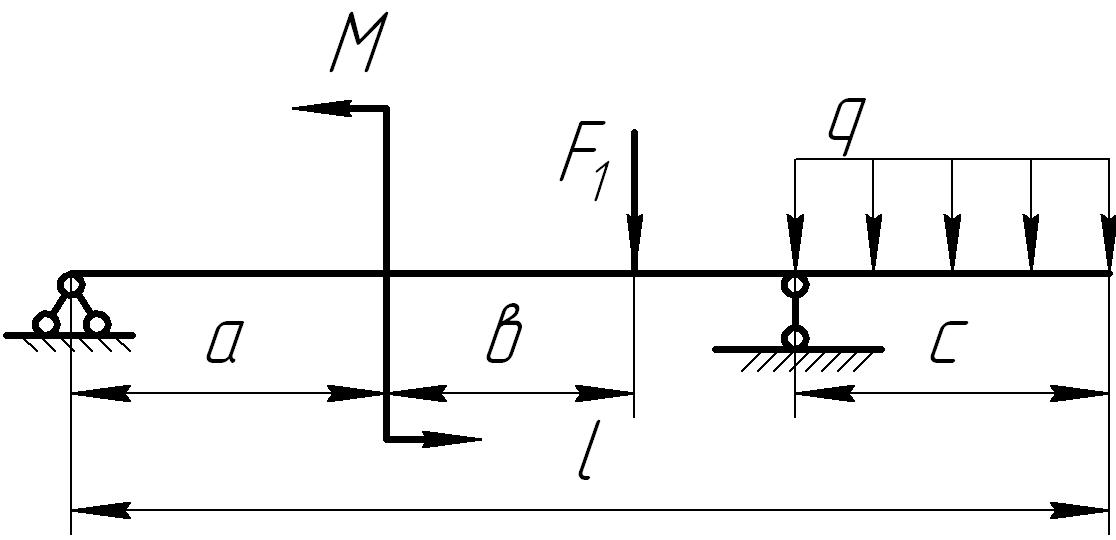
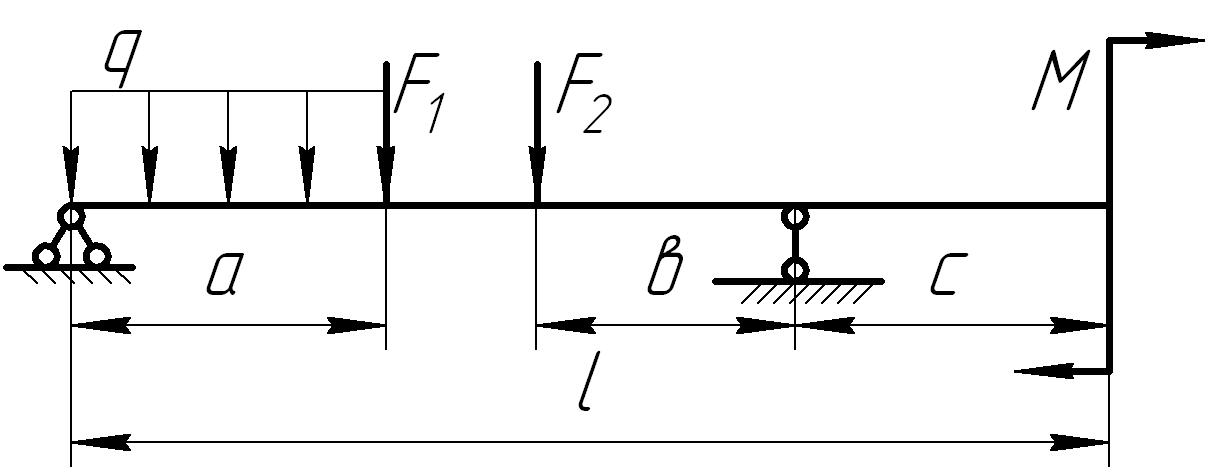
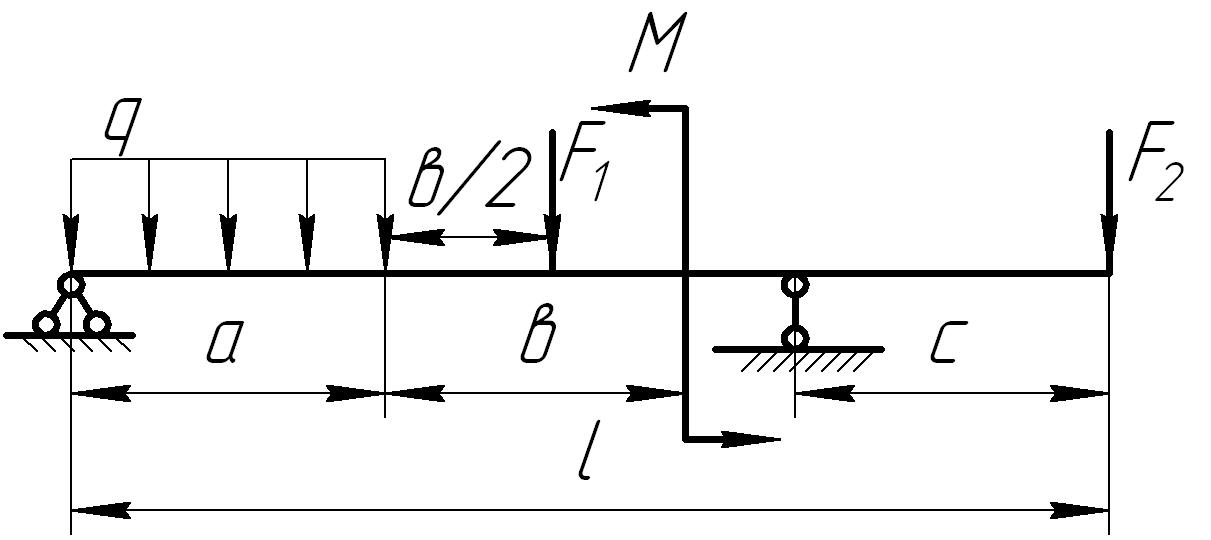
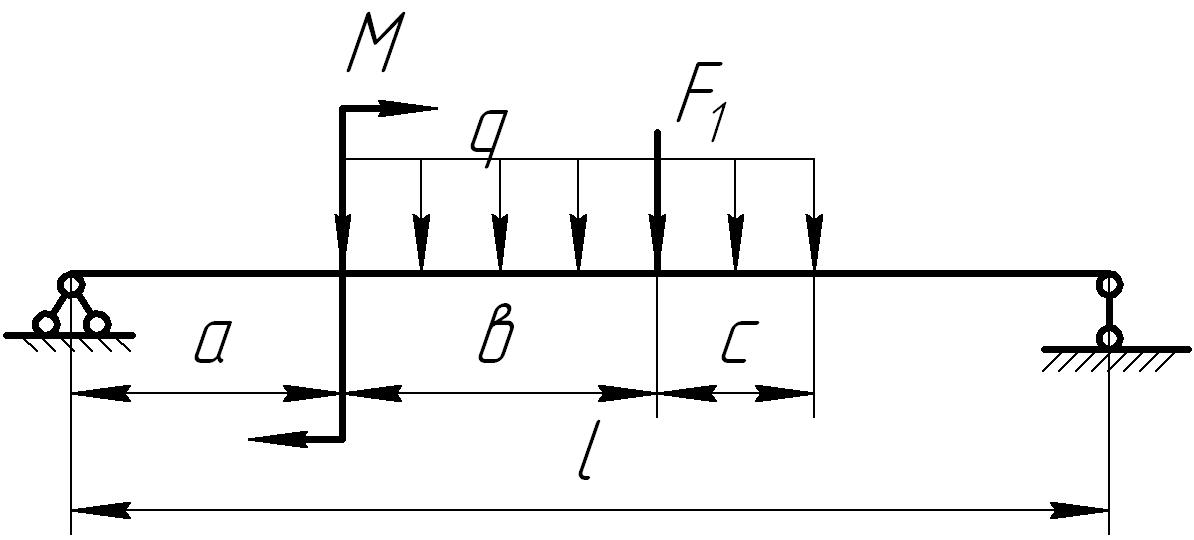
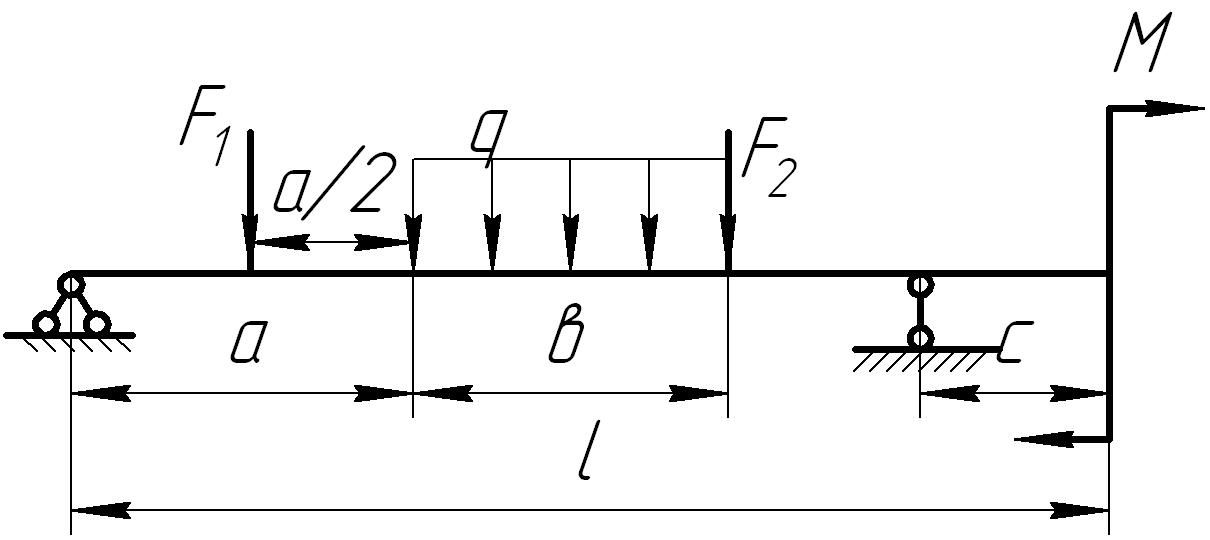
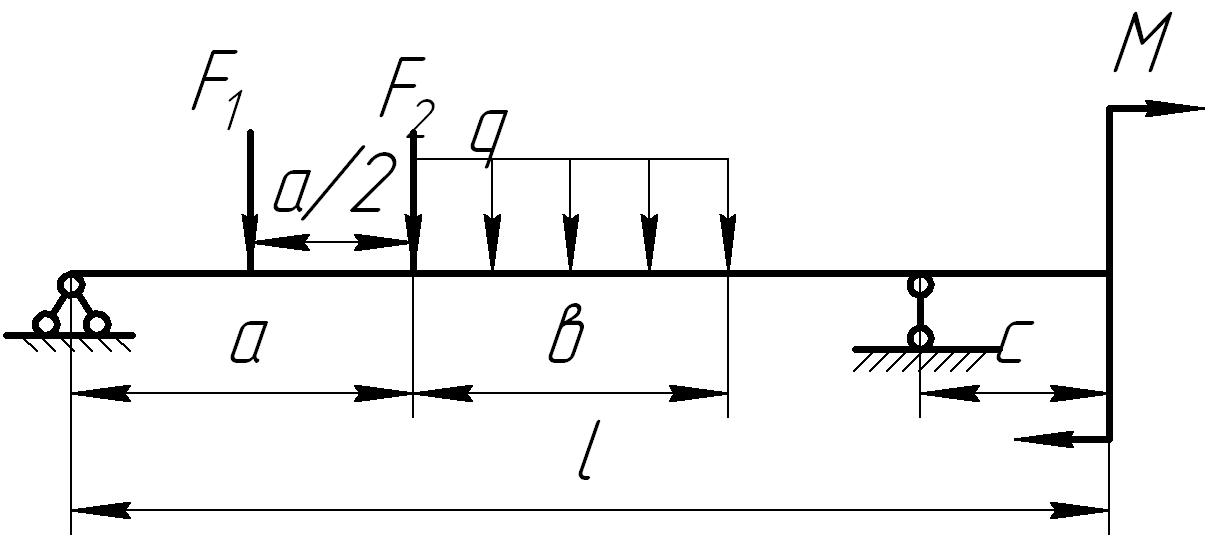
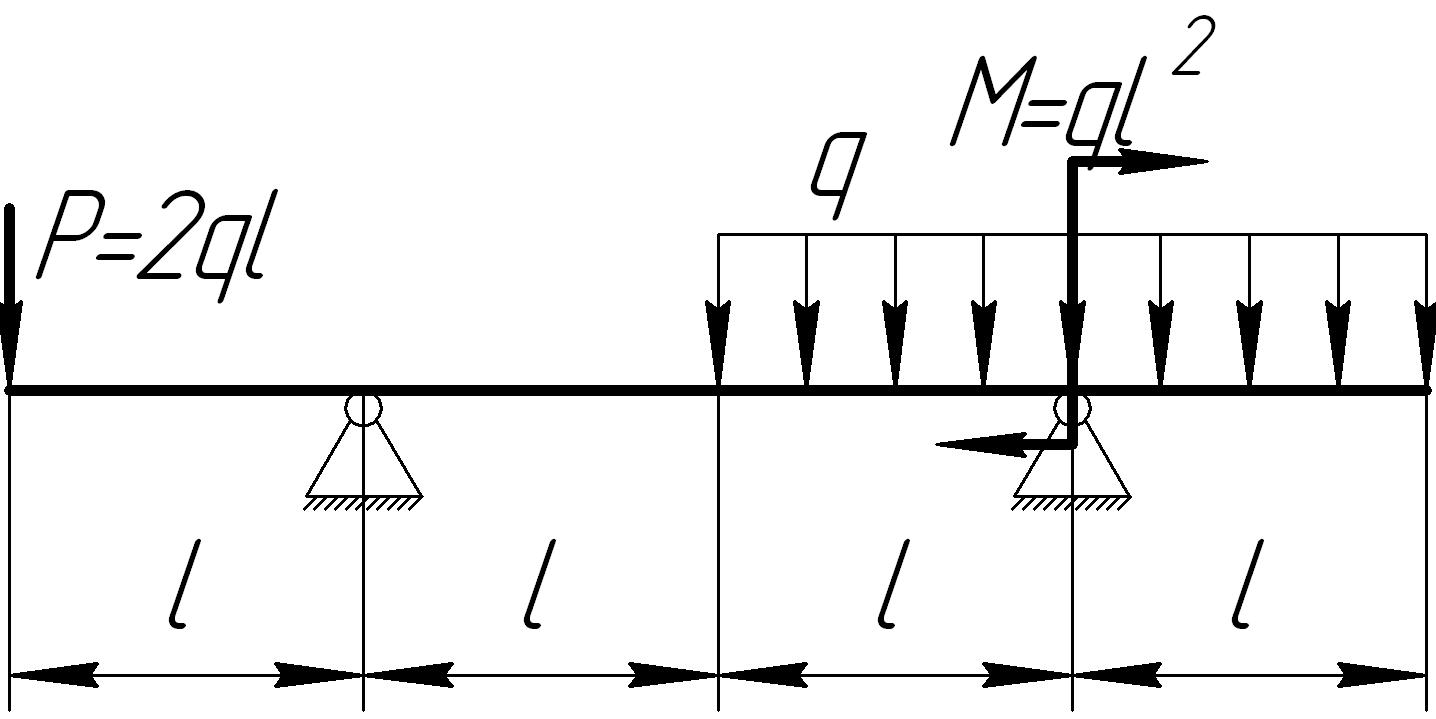
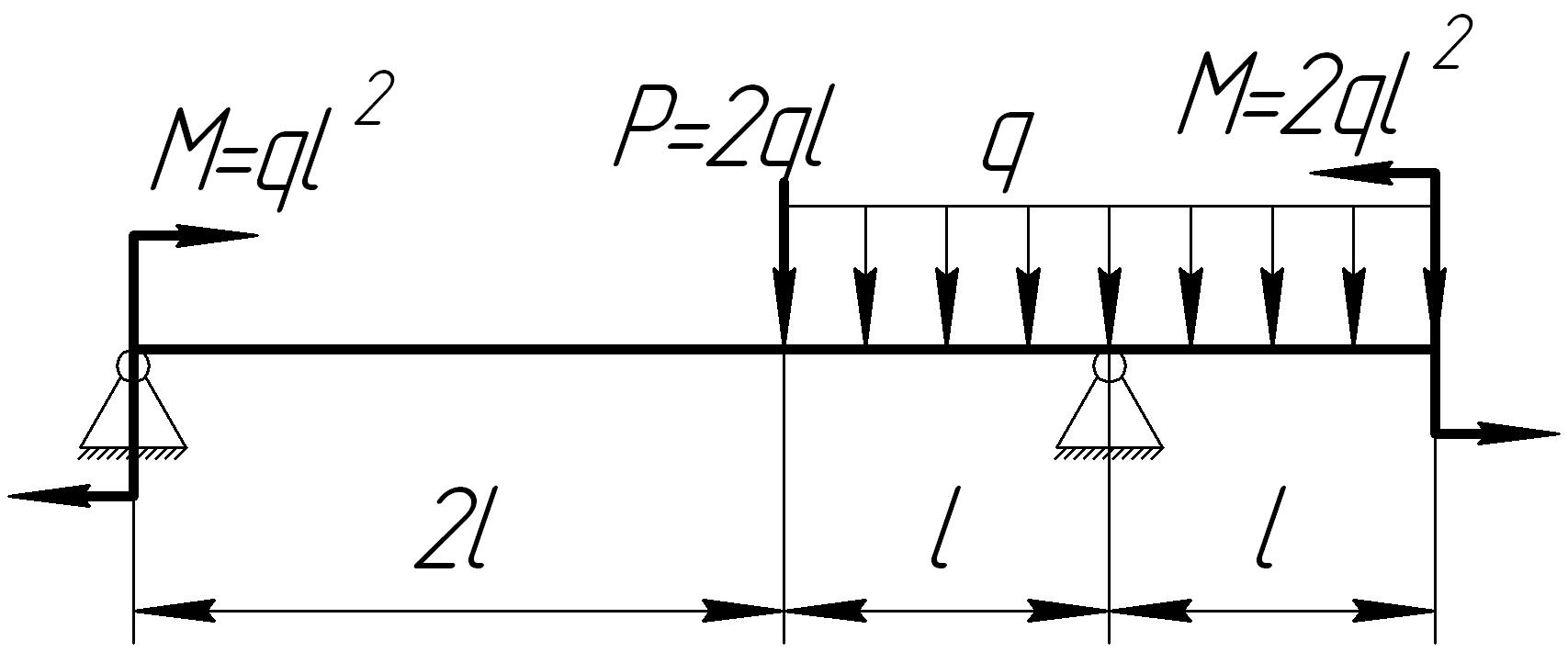
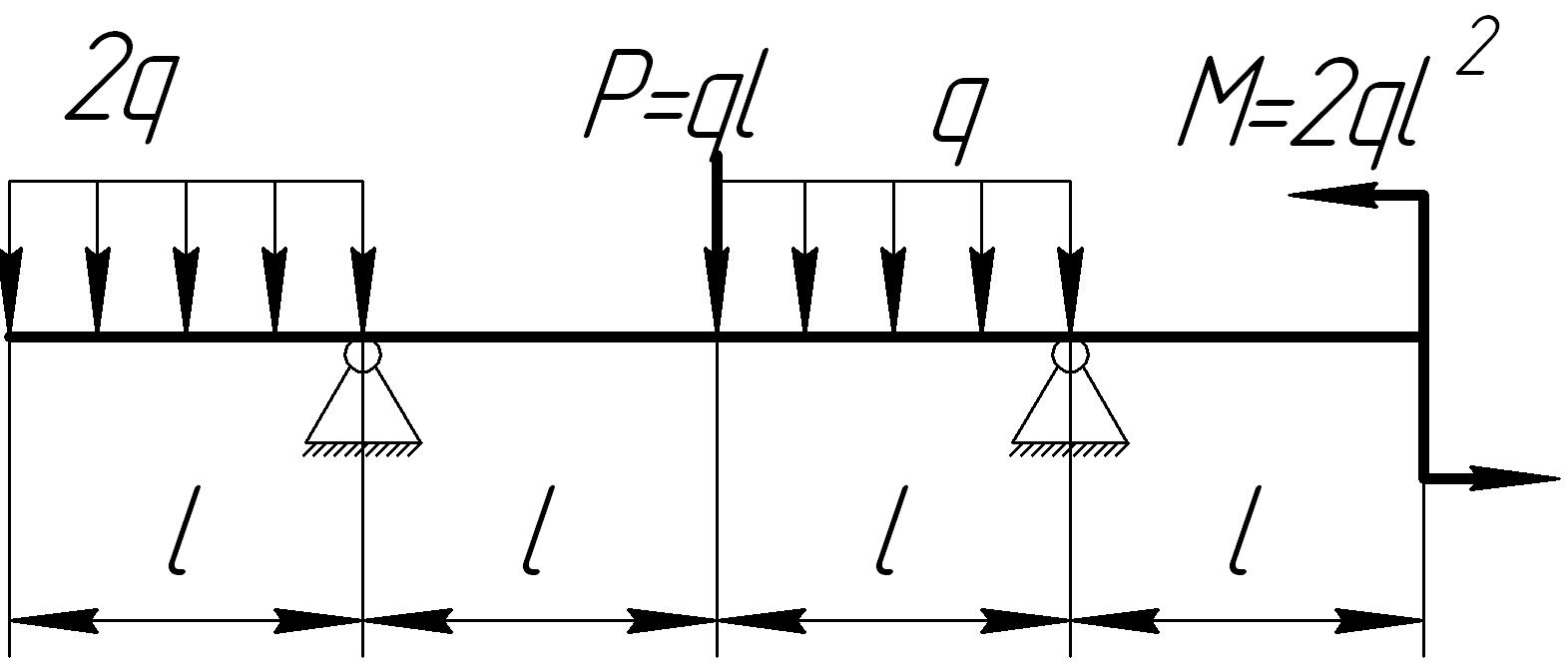
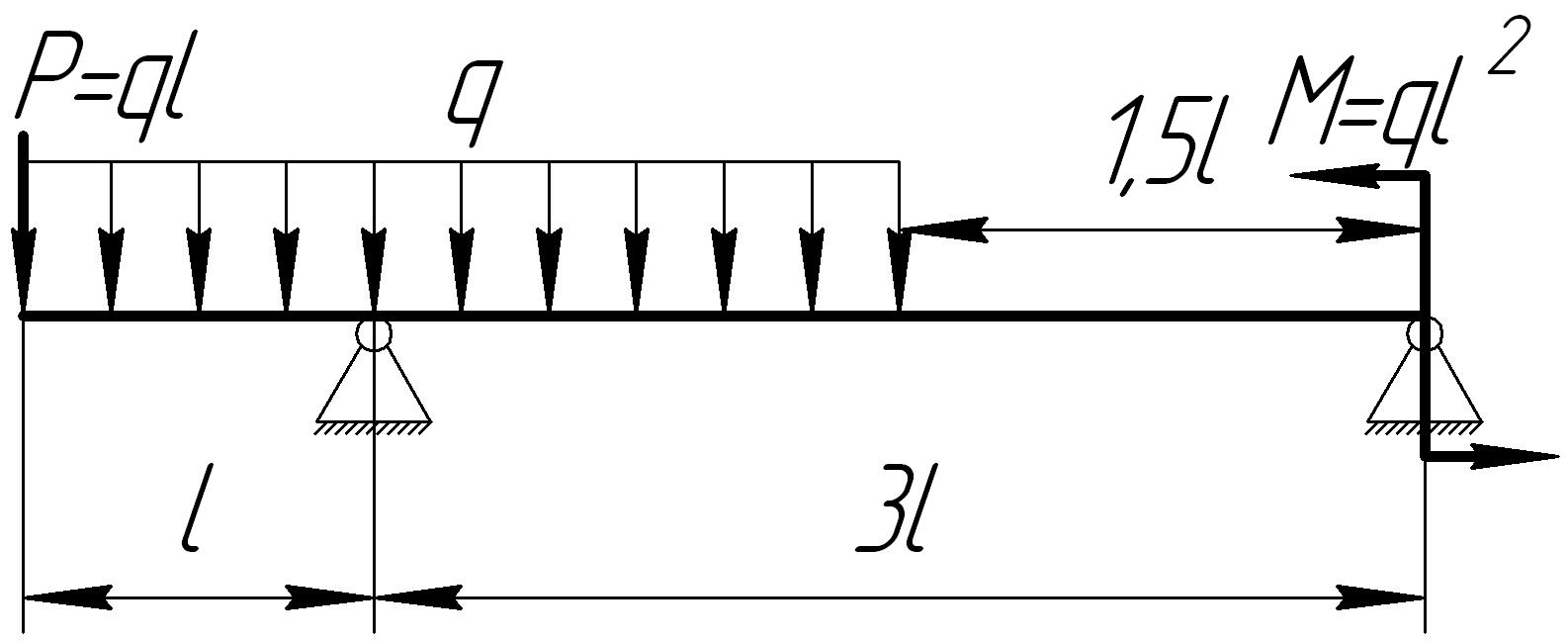
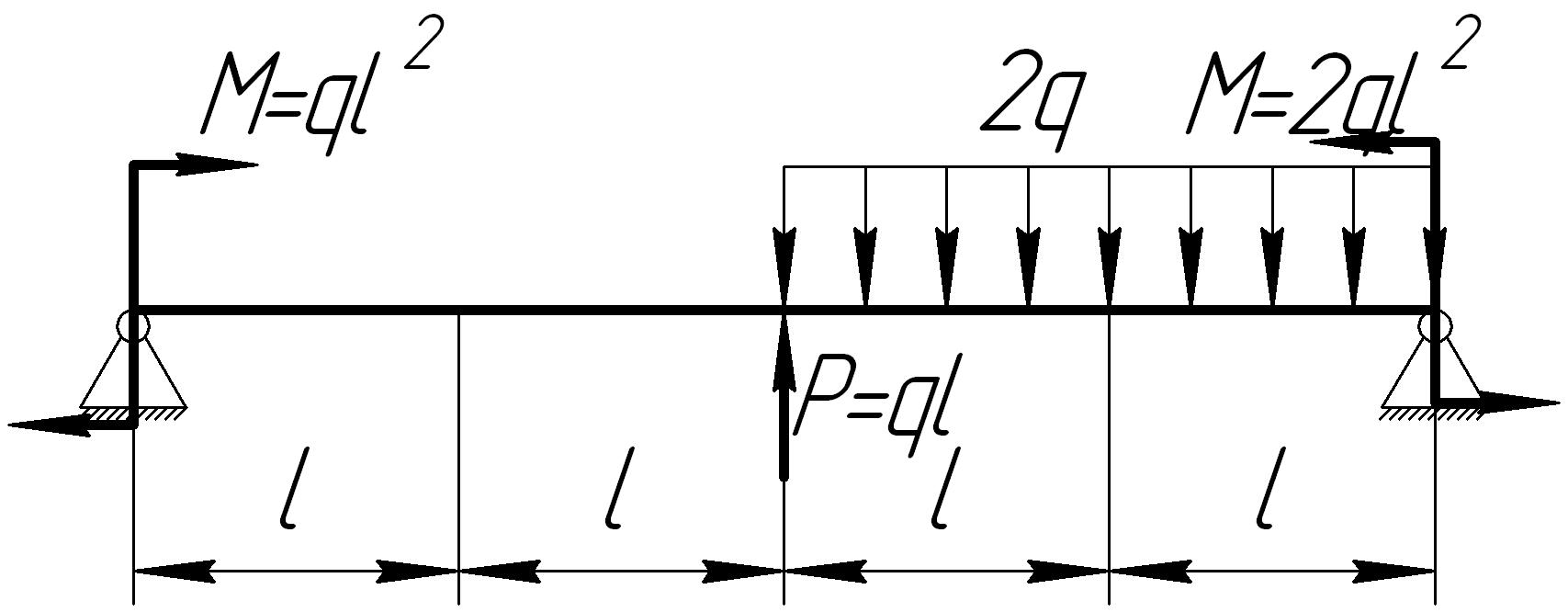
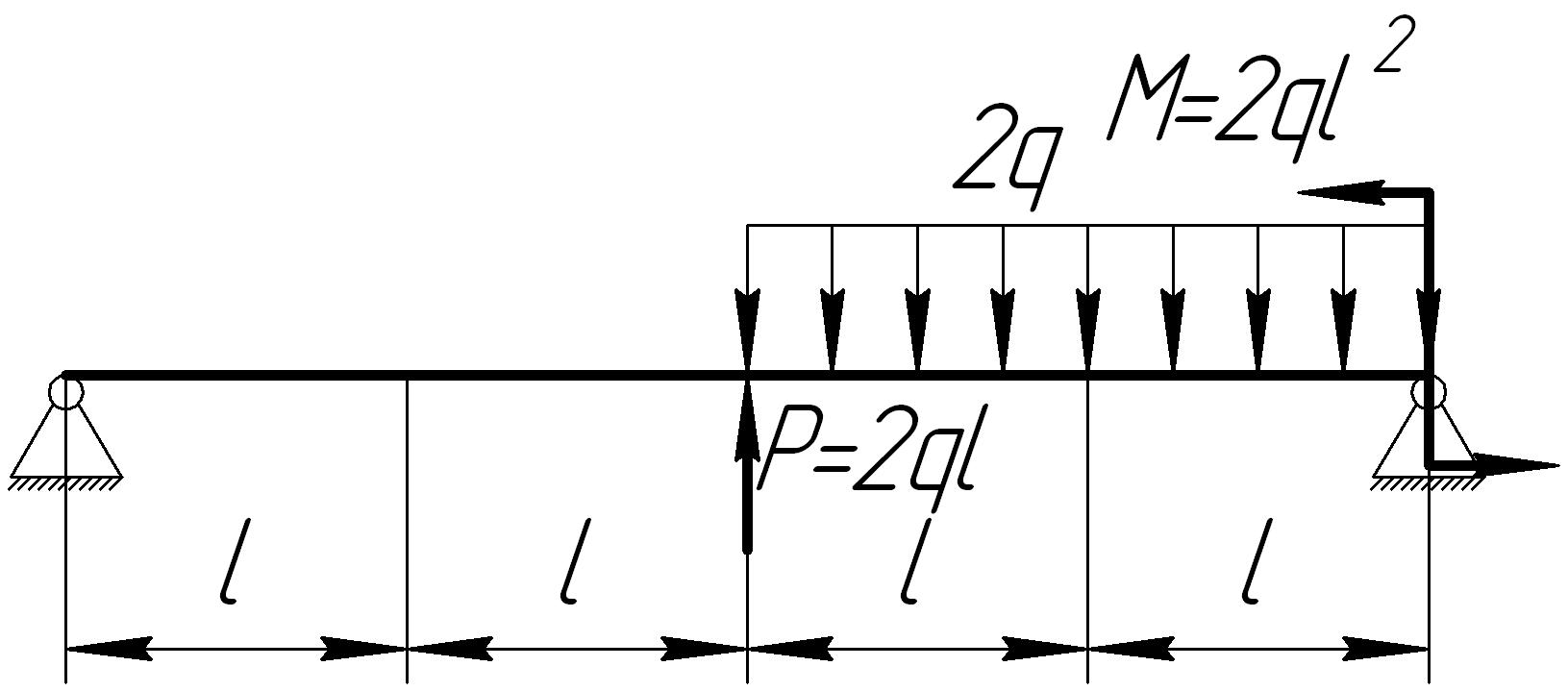
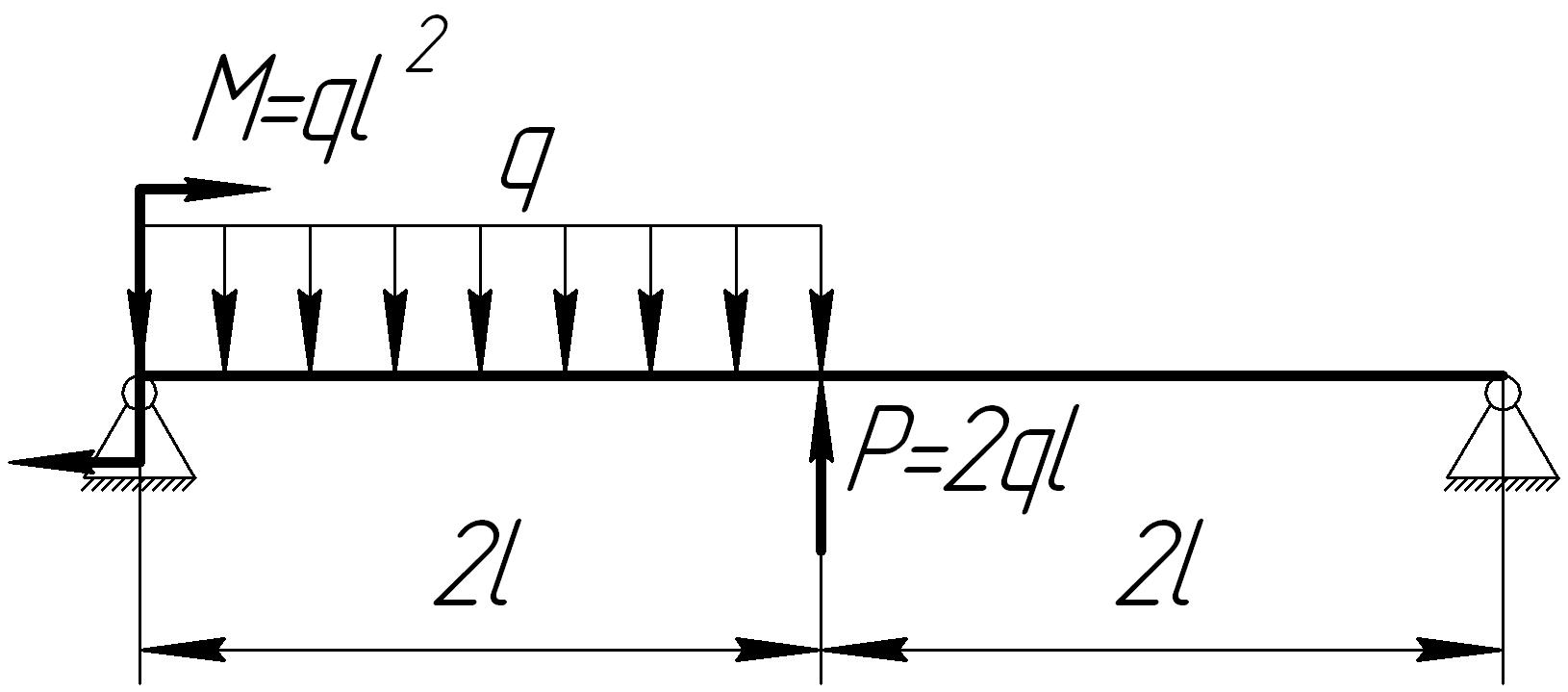
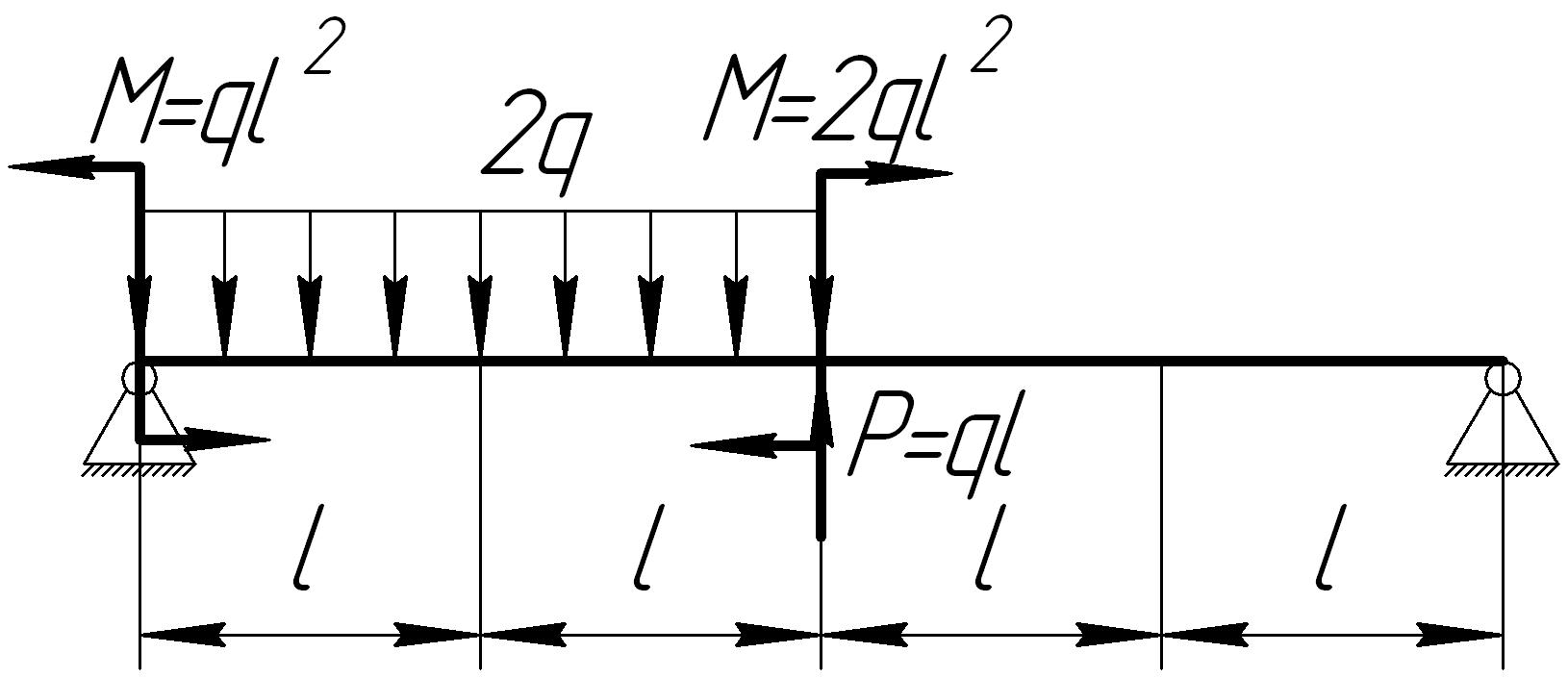
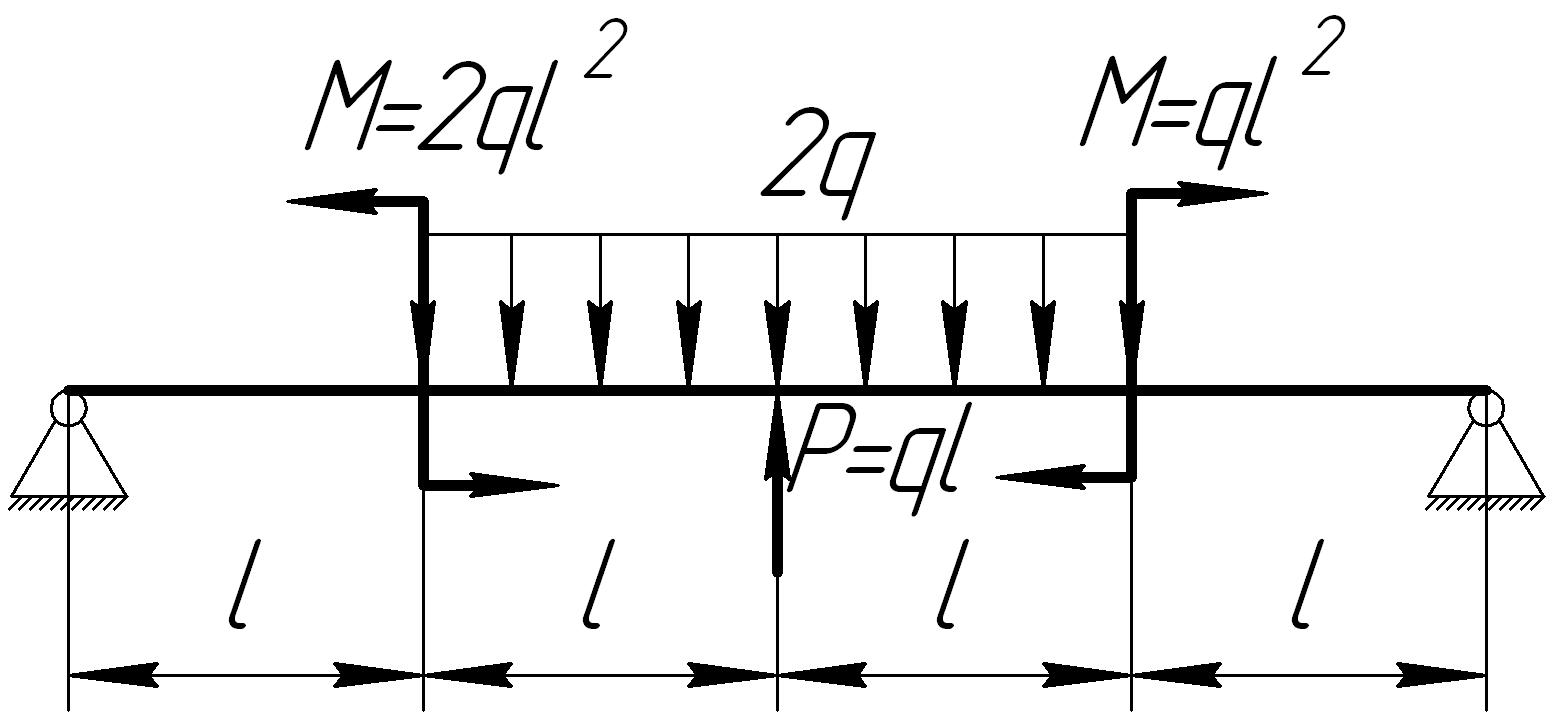
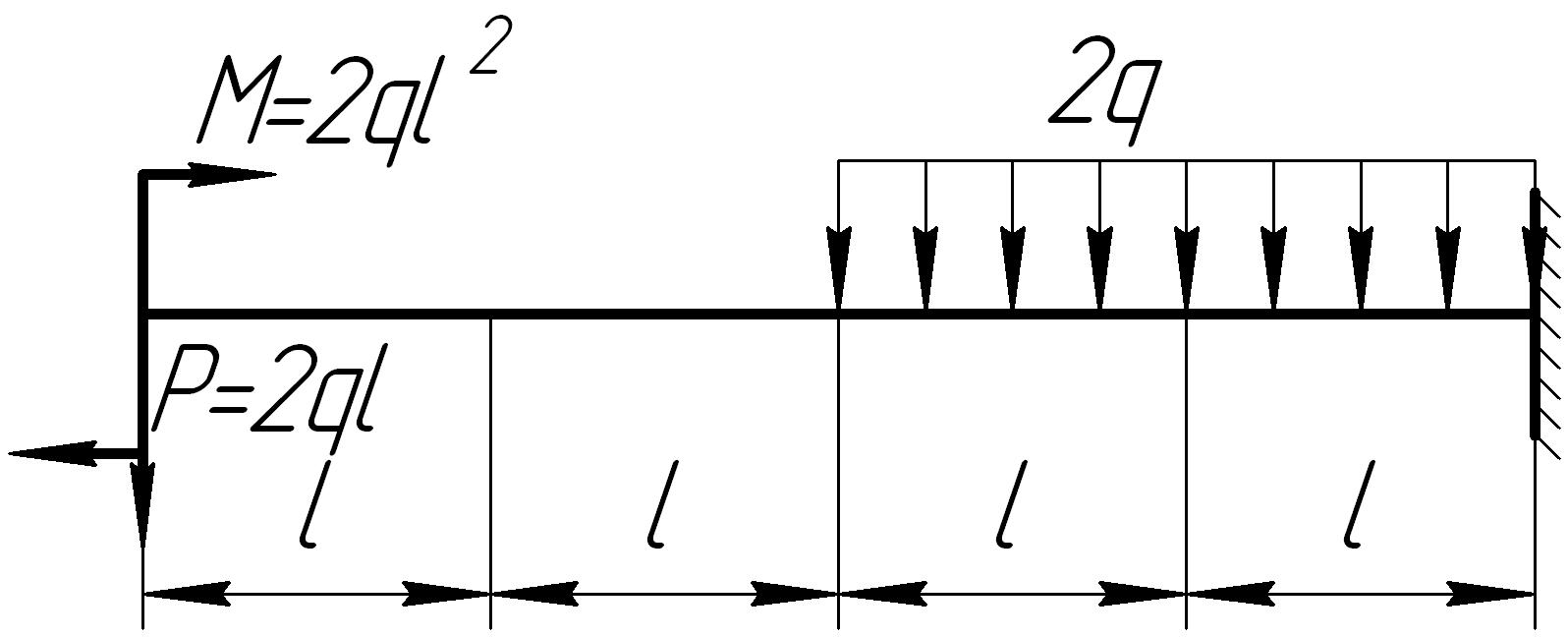
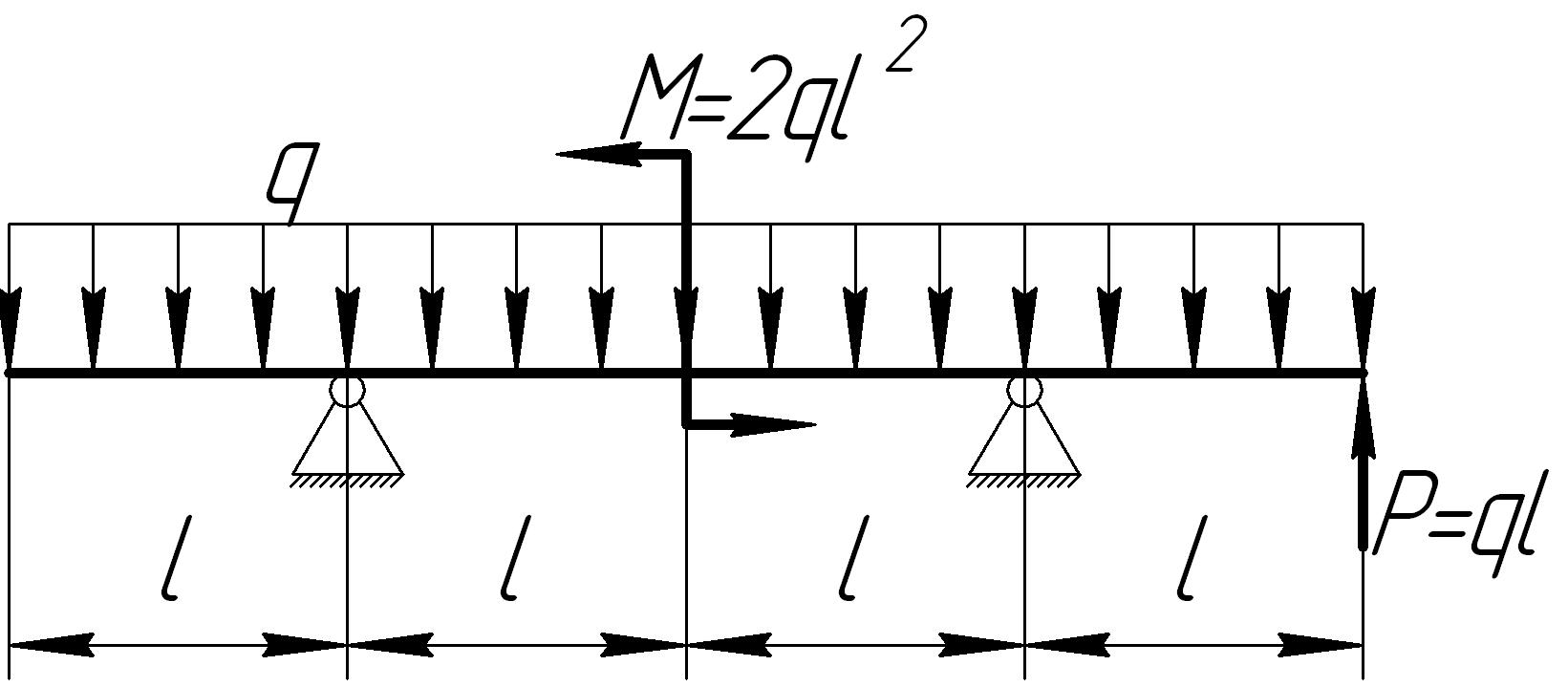
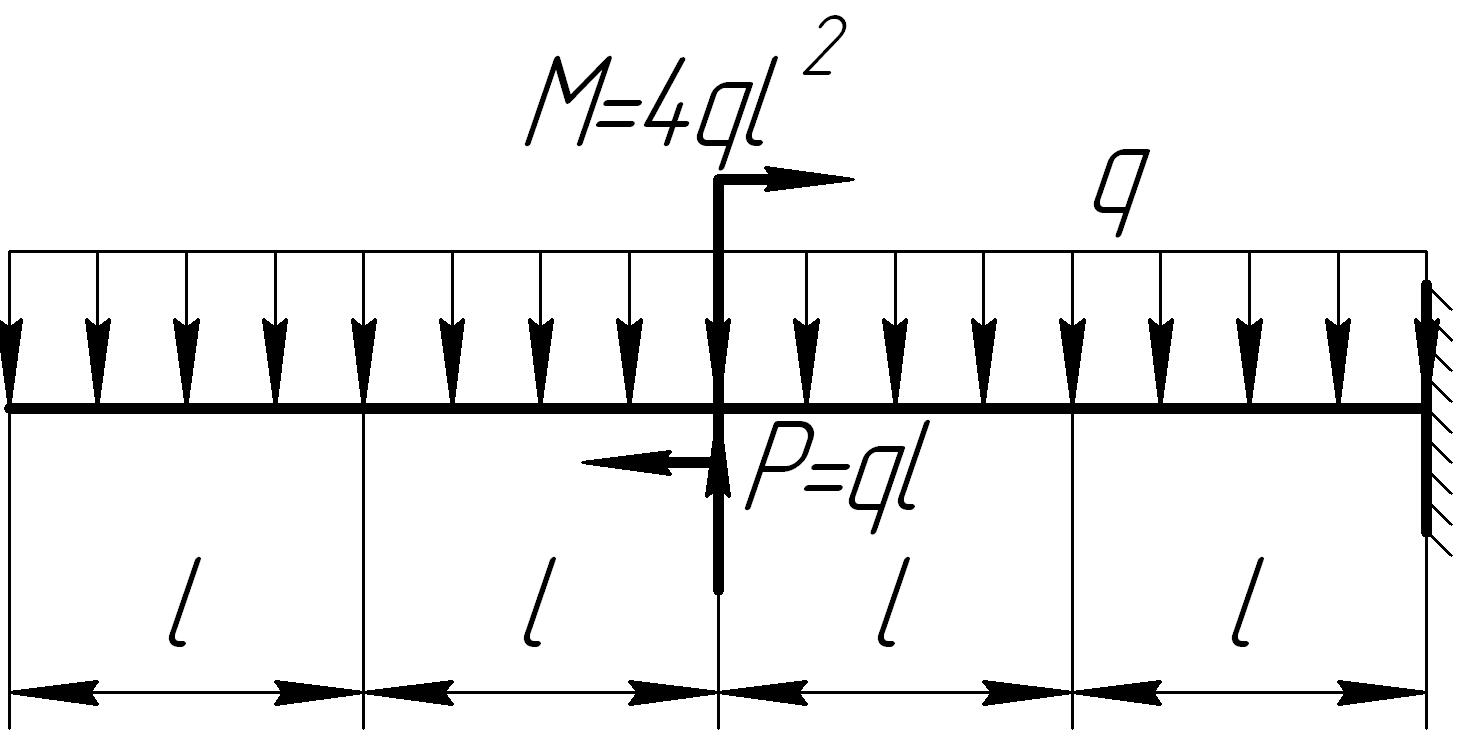
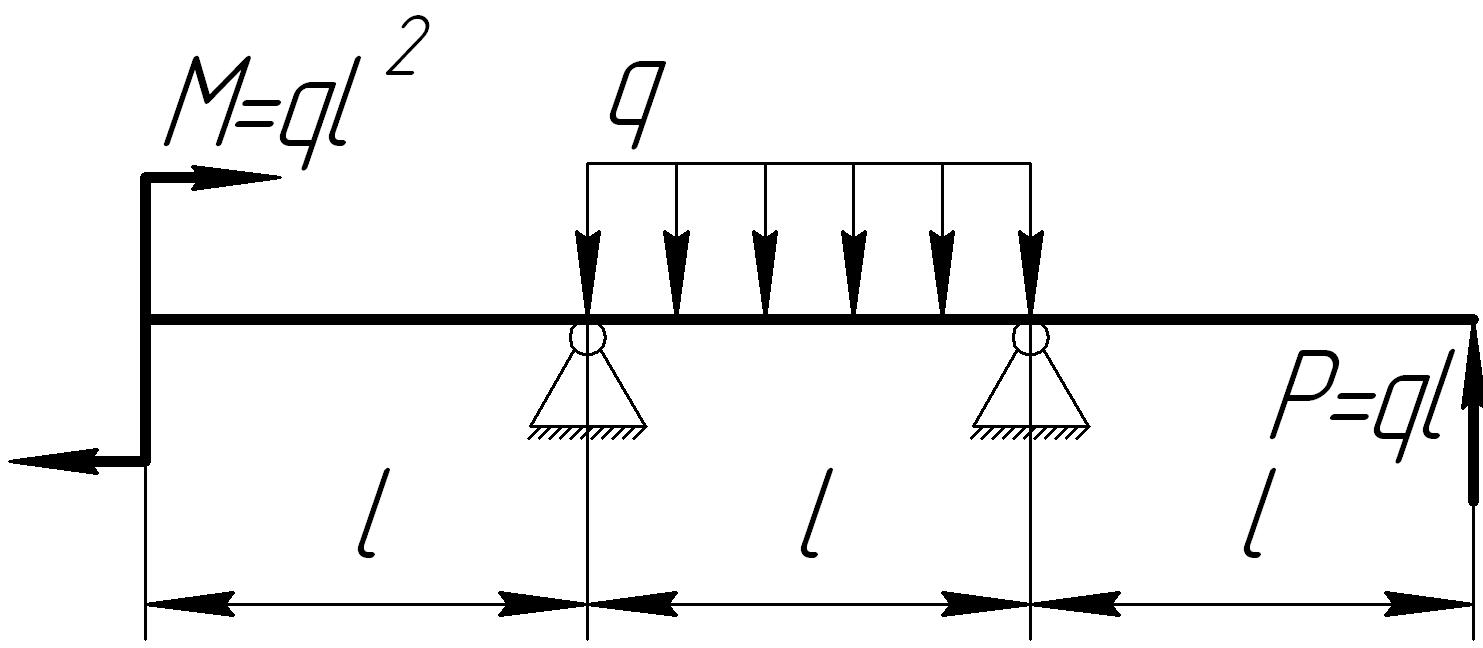
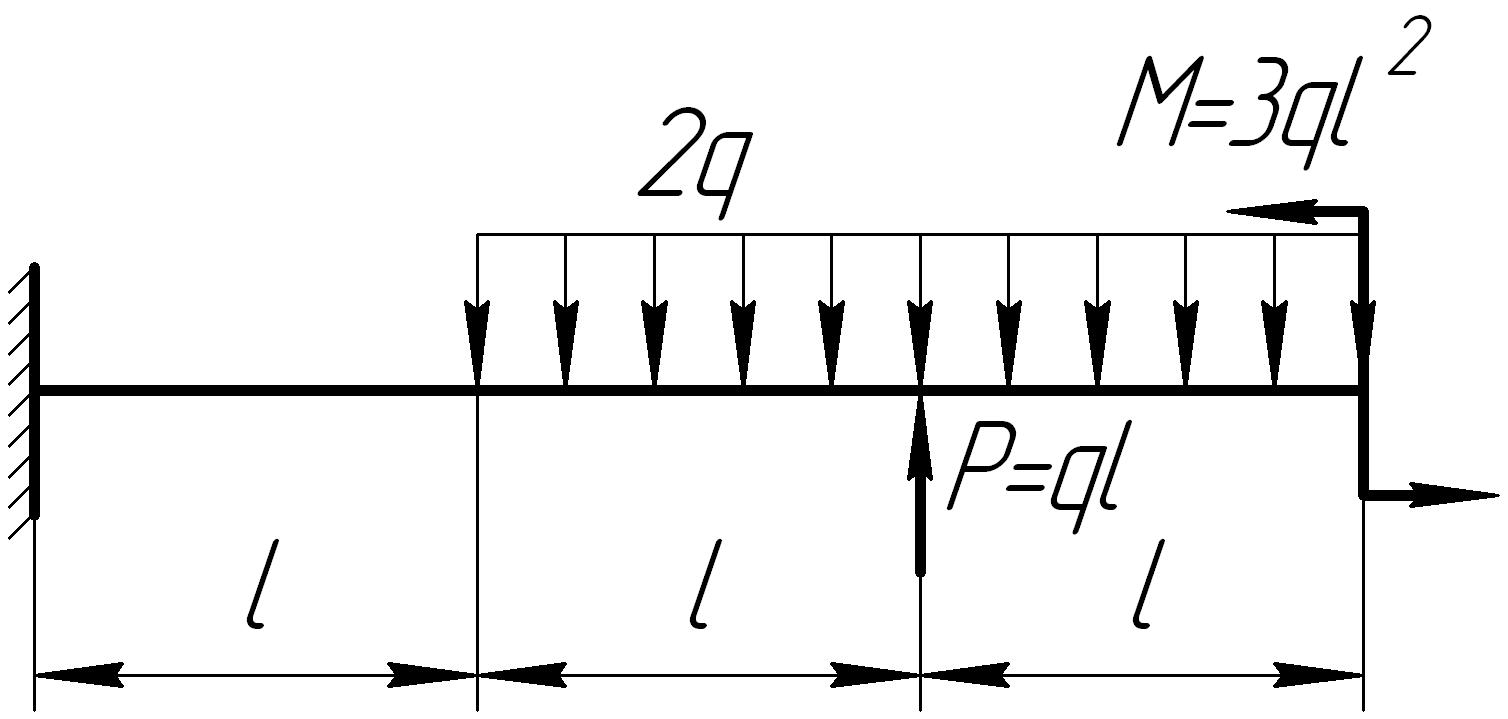
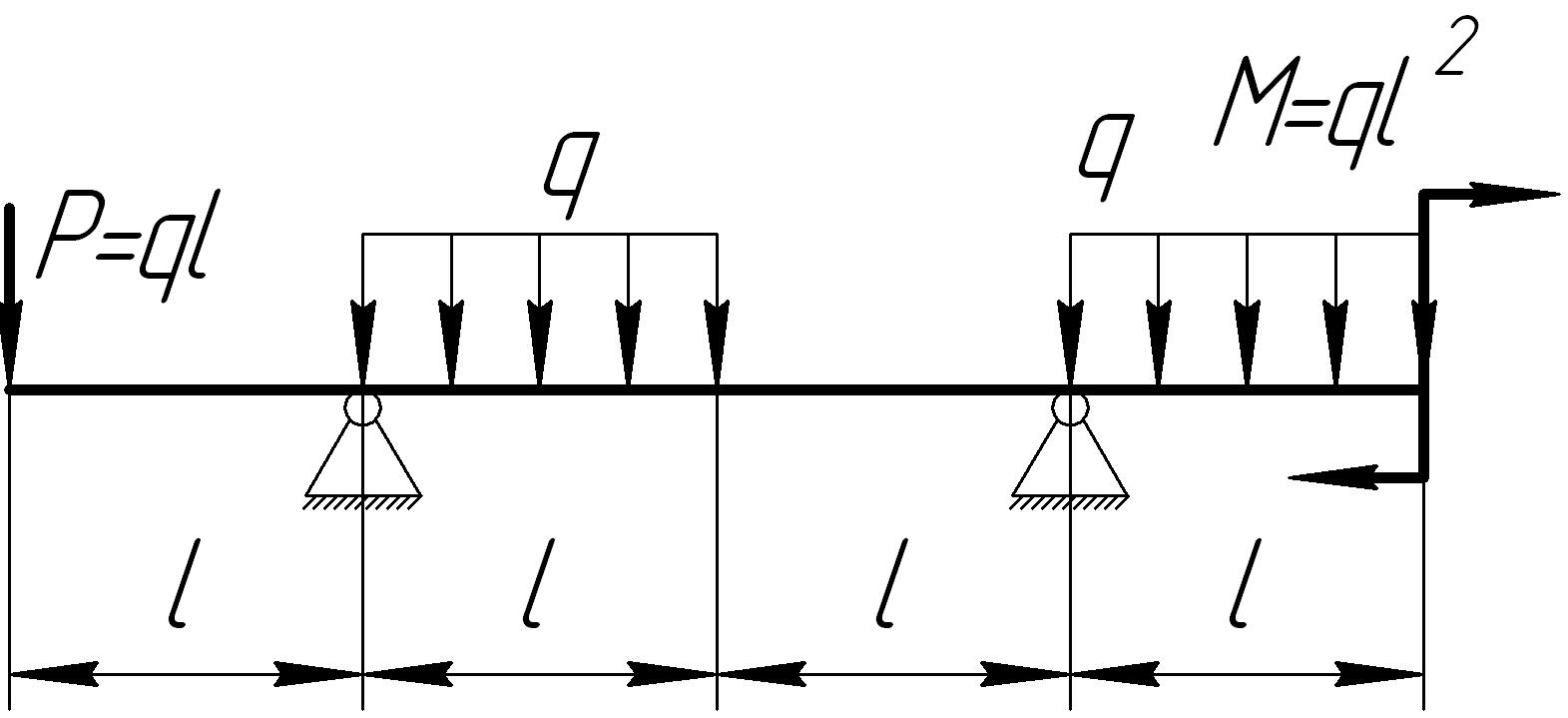
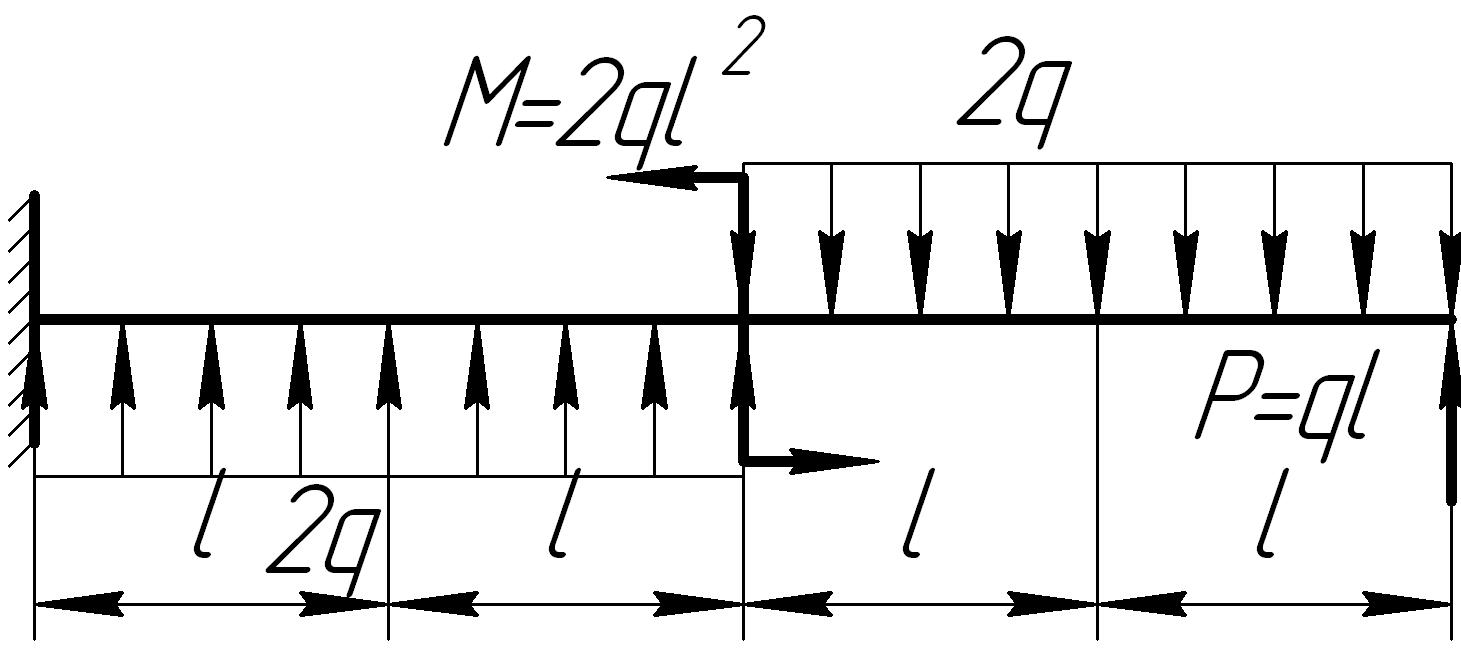
На основании исходных данных (рис. 6.8) построить эпюру внутренних силовых факторов при изгибе балок.
1. |
|
2. |
|
3. |
|
4. |
|
Рис. 6.8
5. |
|
6. |
|
7. |
|
8. |
|
9. |
|
10. |
|
11. |
|
12. |
|
13. |
|
14. |
|
15. |
|
16. |
|
Рис. 6.8
17. |
|
18. |
|
19. |
|
20. |
|
21. |
|
22. |
|
23. |
|
24. |
|
25. |
|
26. |
|
27. |
|
28. |
|
Рис. 6.8
29. |
|
30. |
|
Рис. 6.8
Задача 9
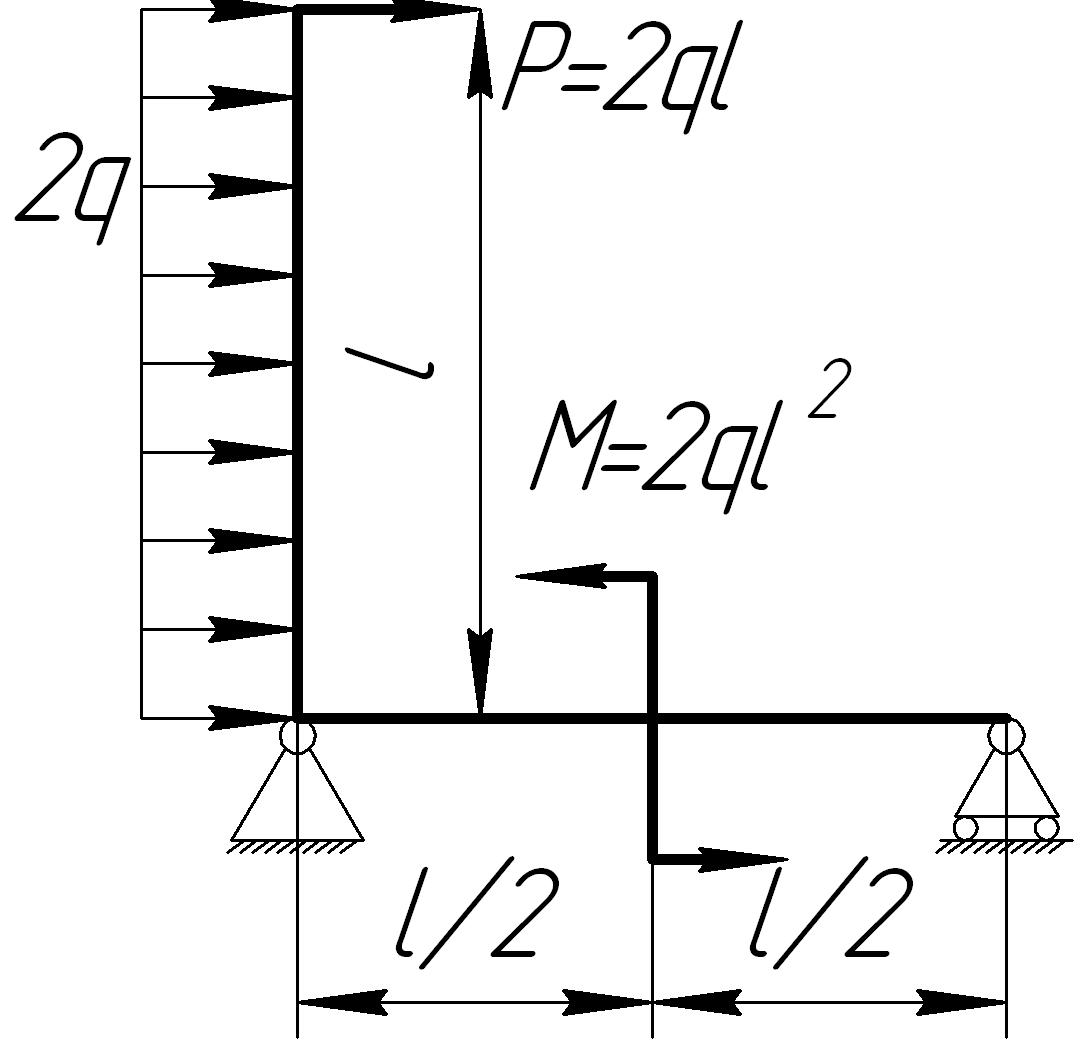
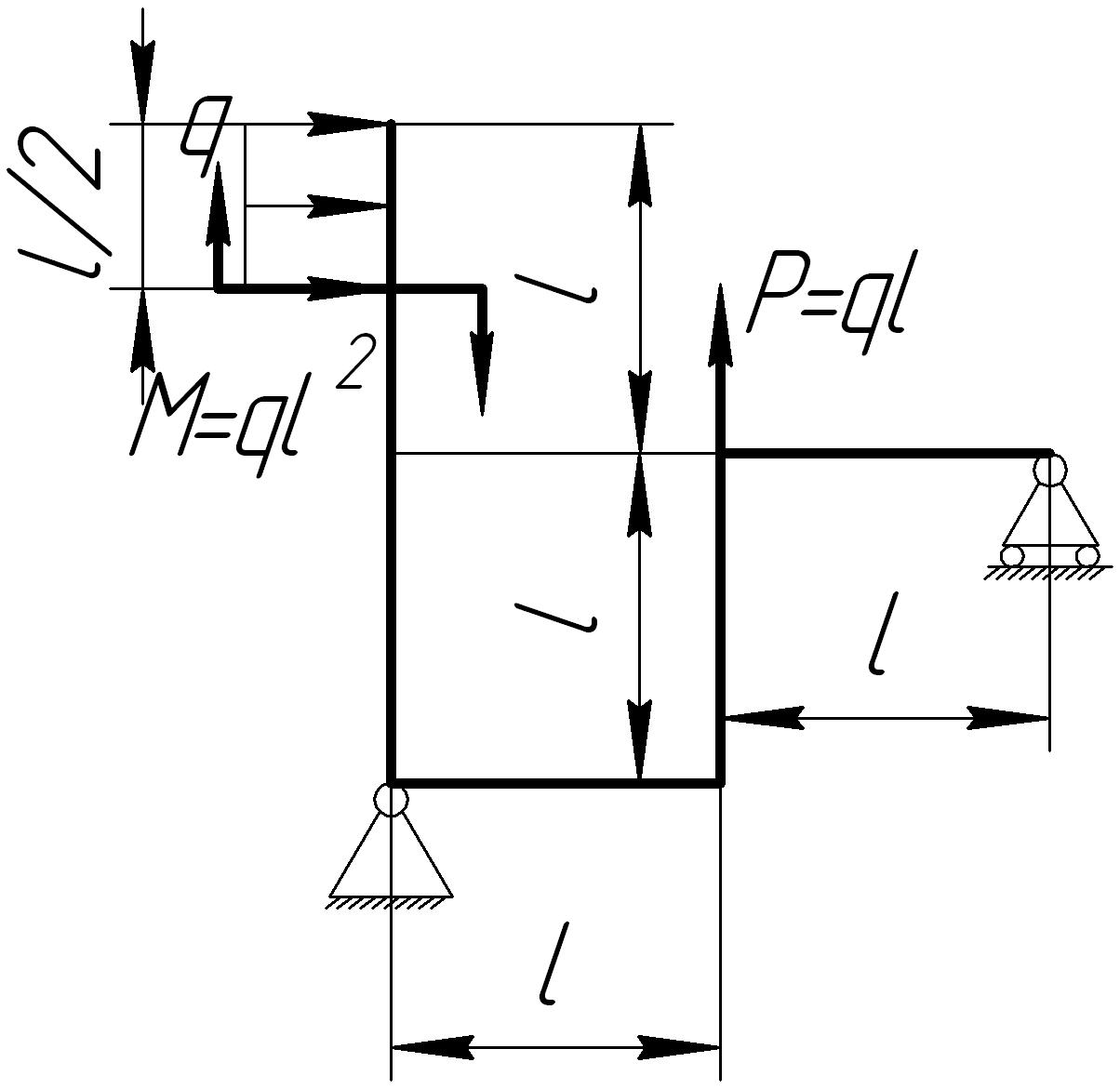
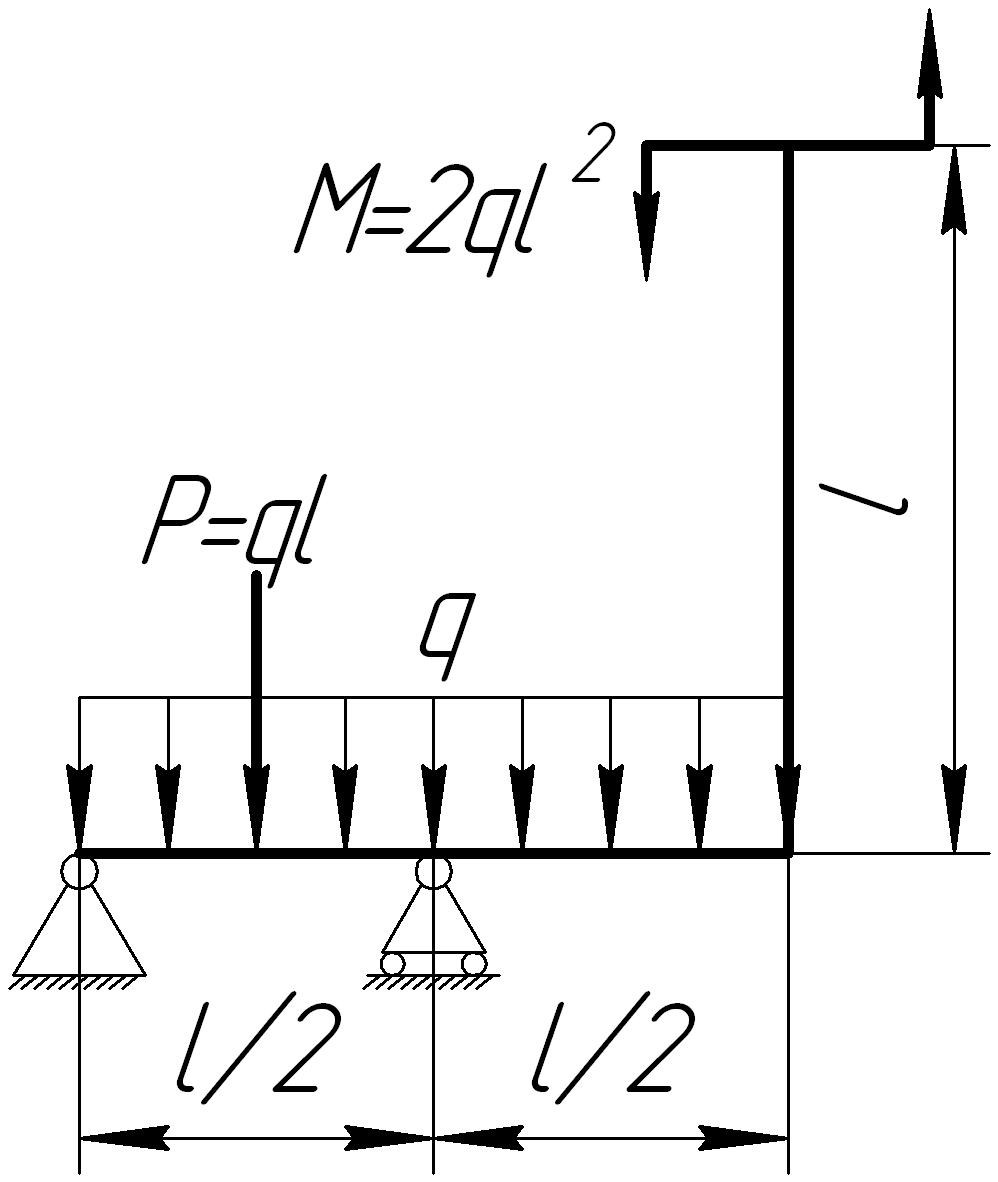
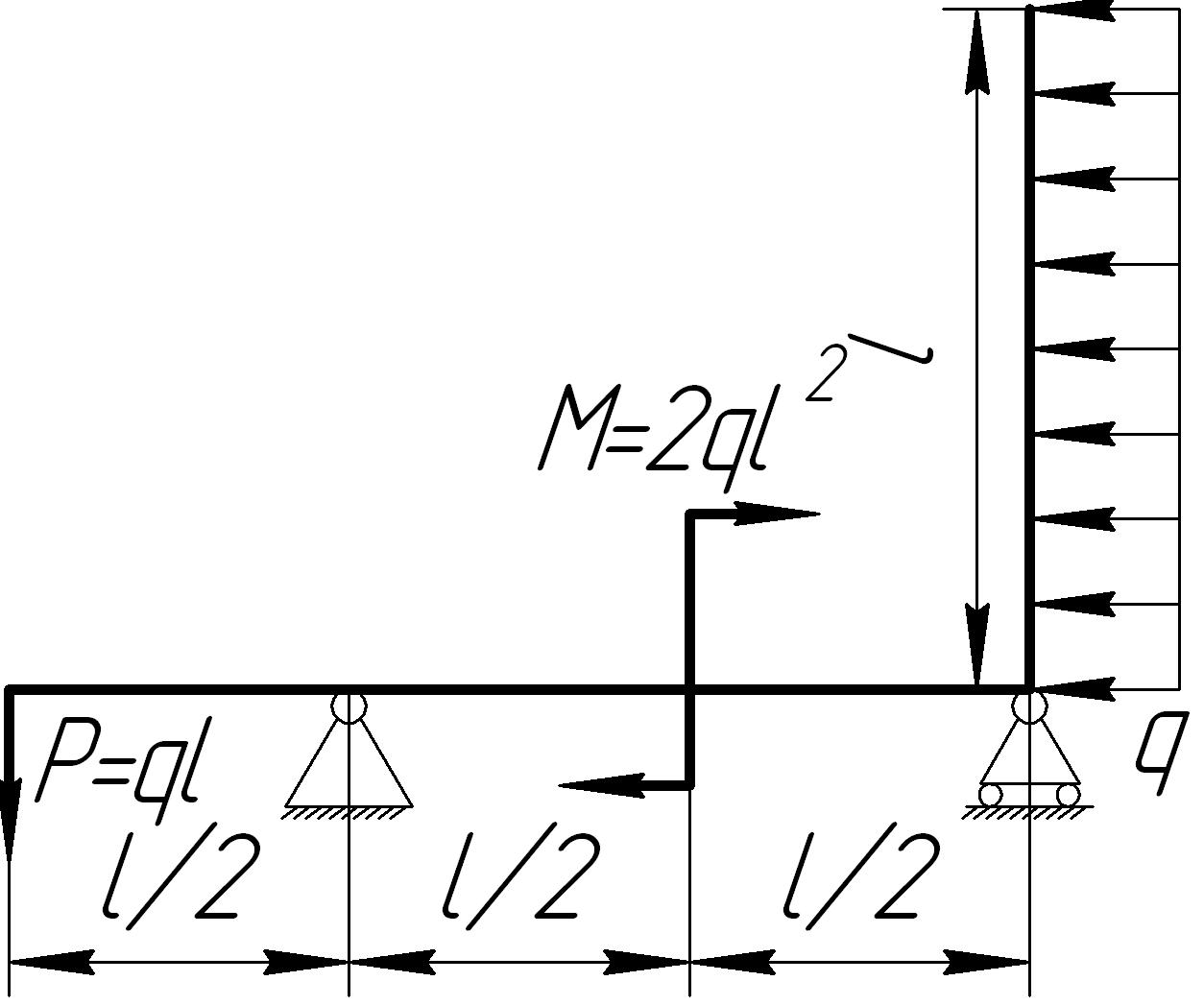
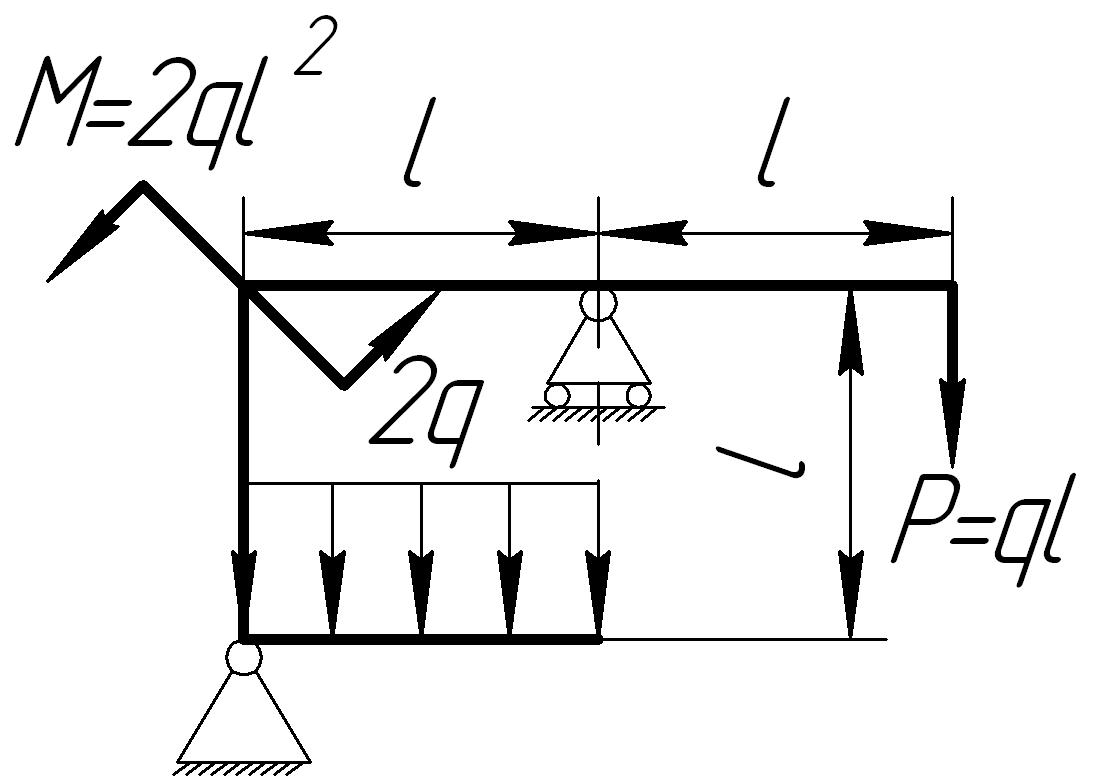
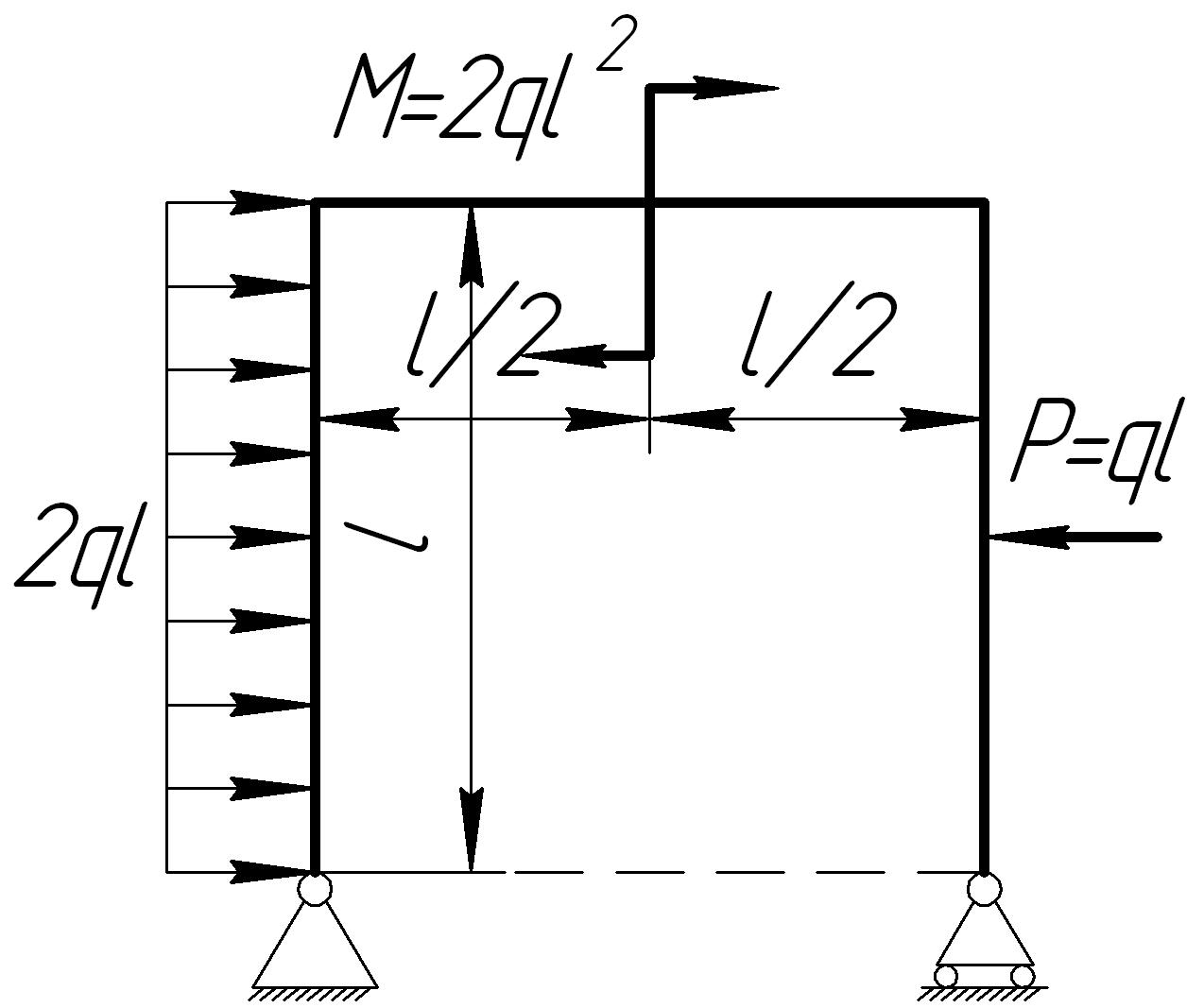
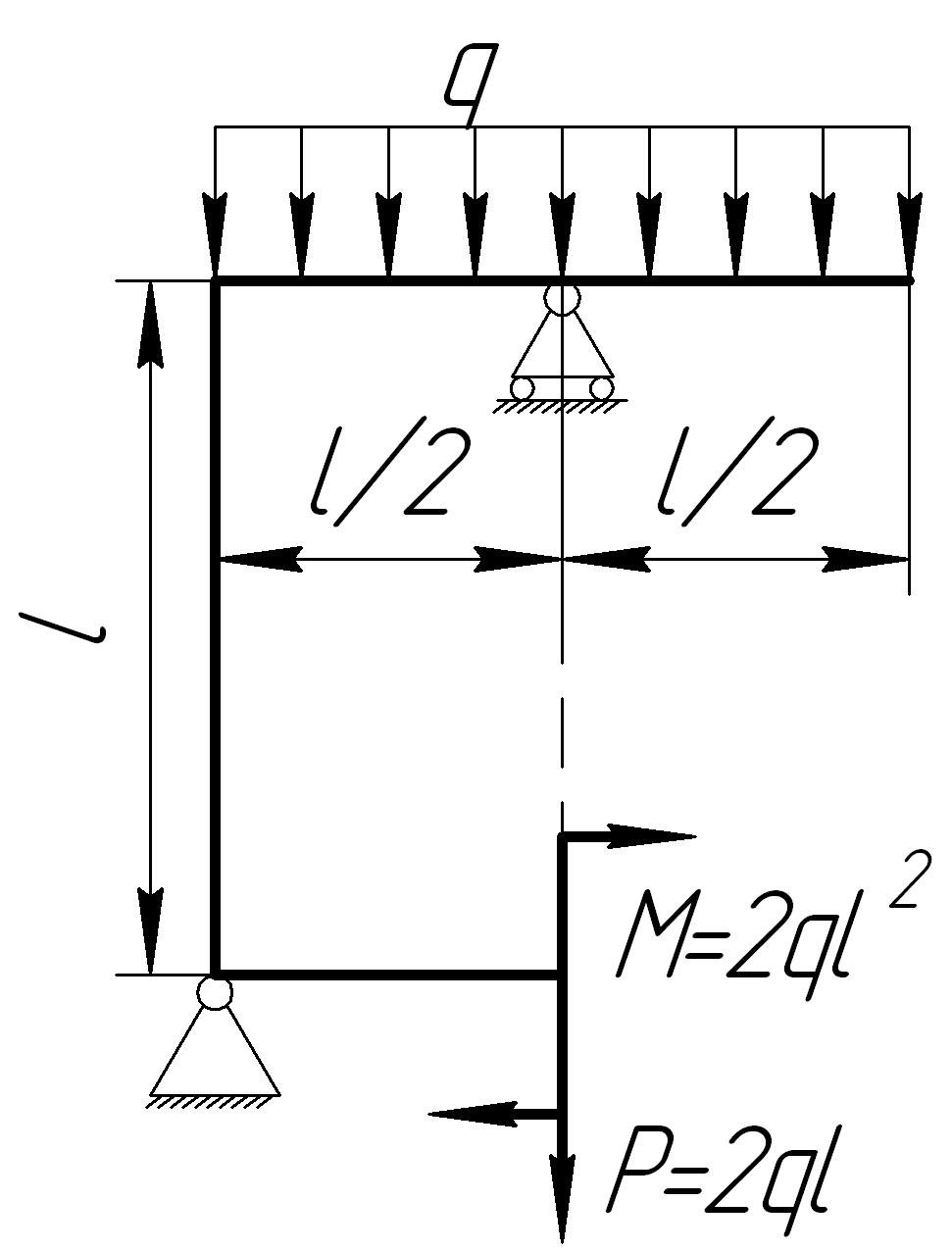
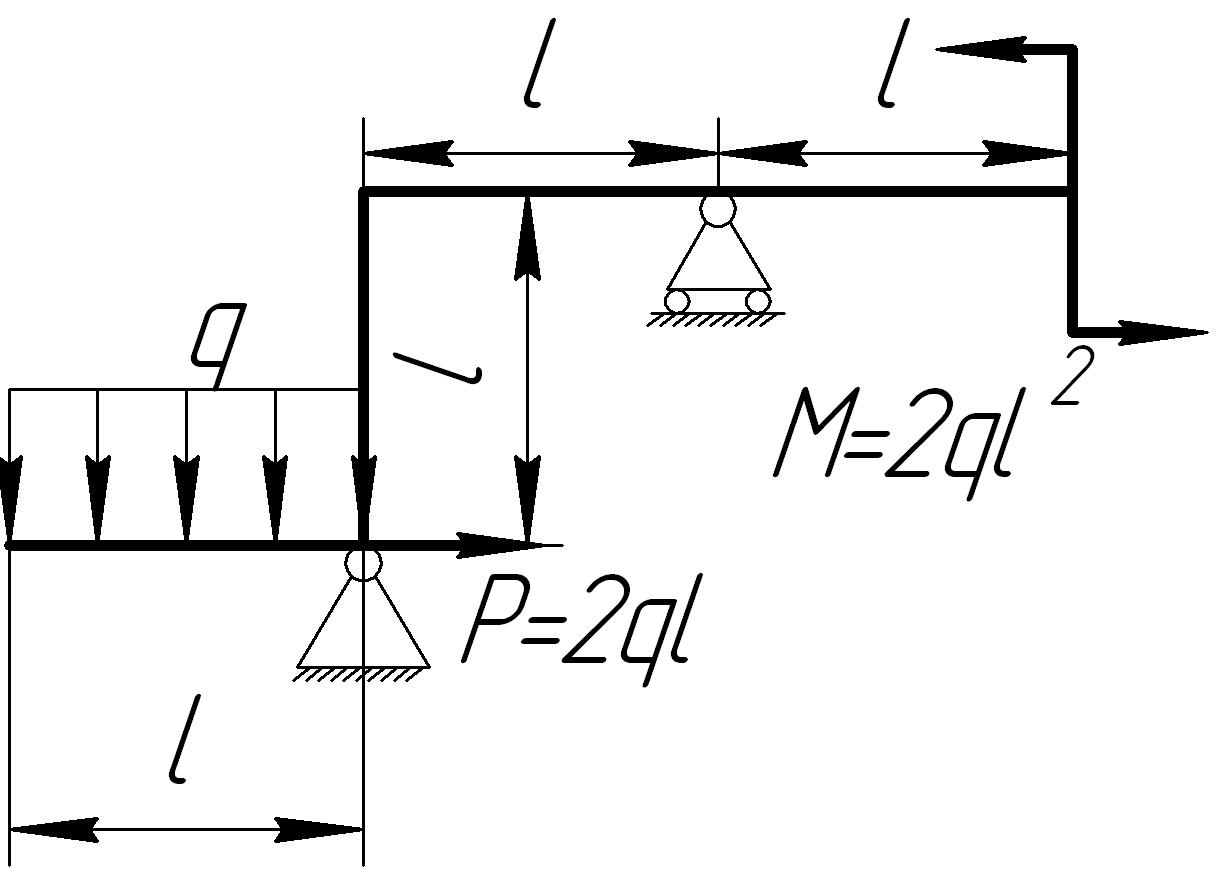
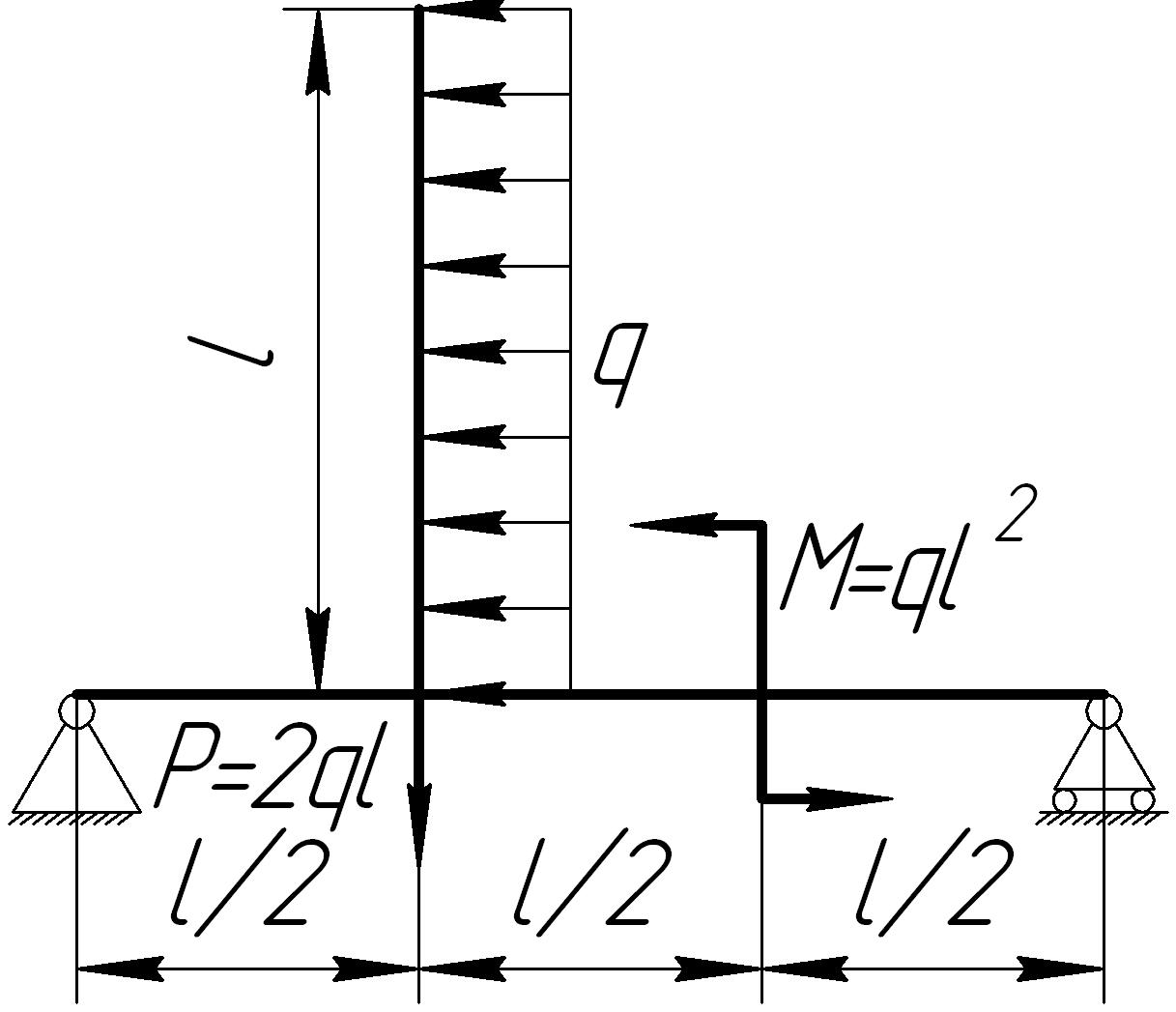
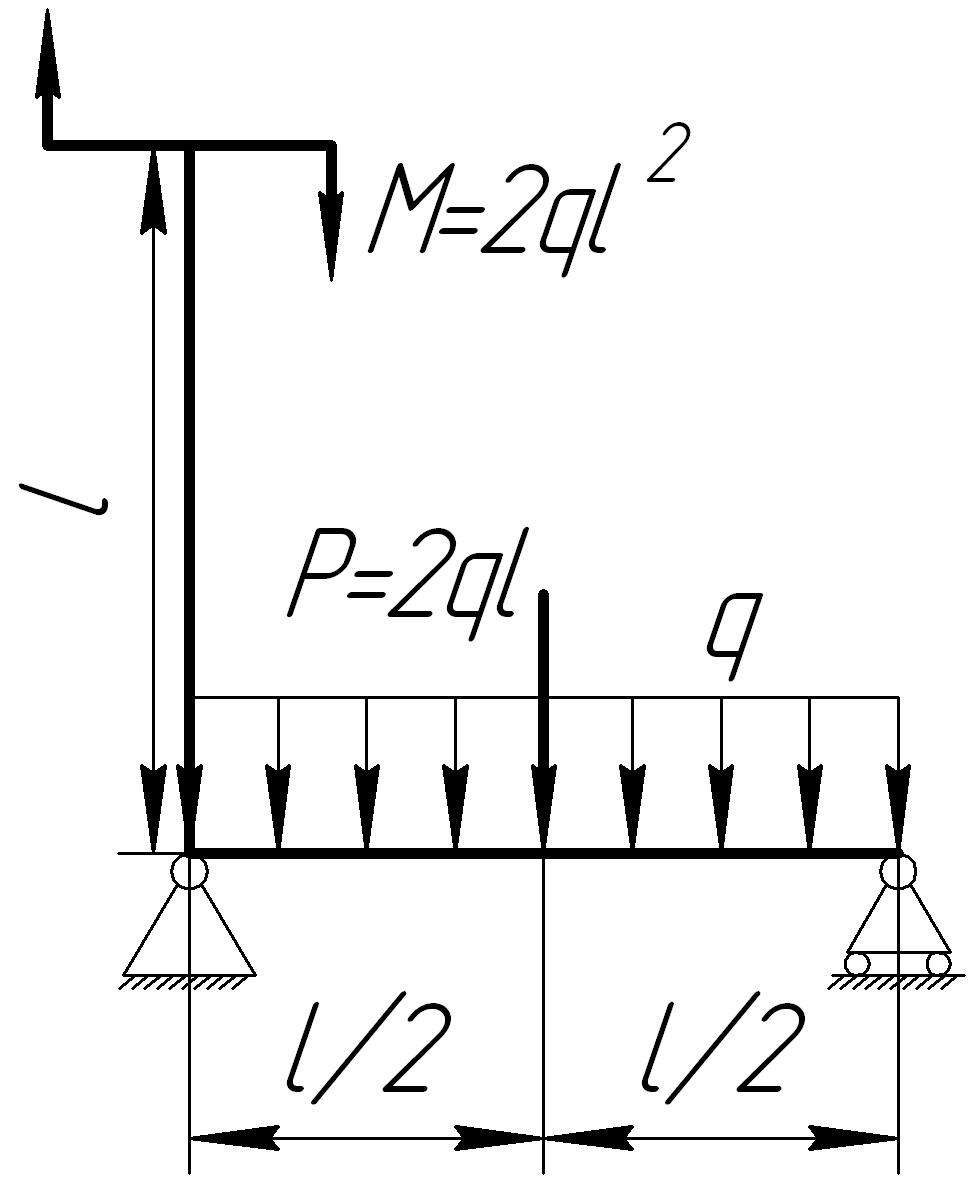
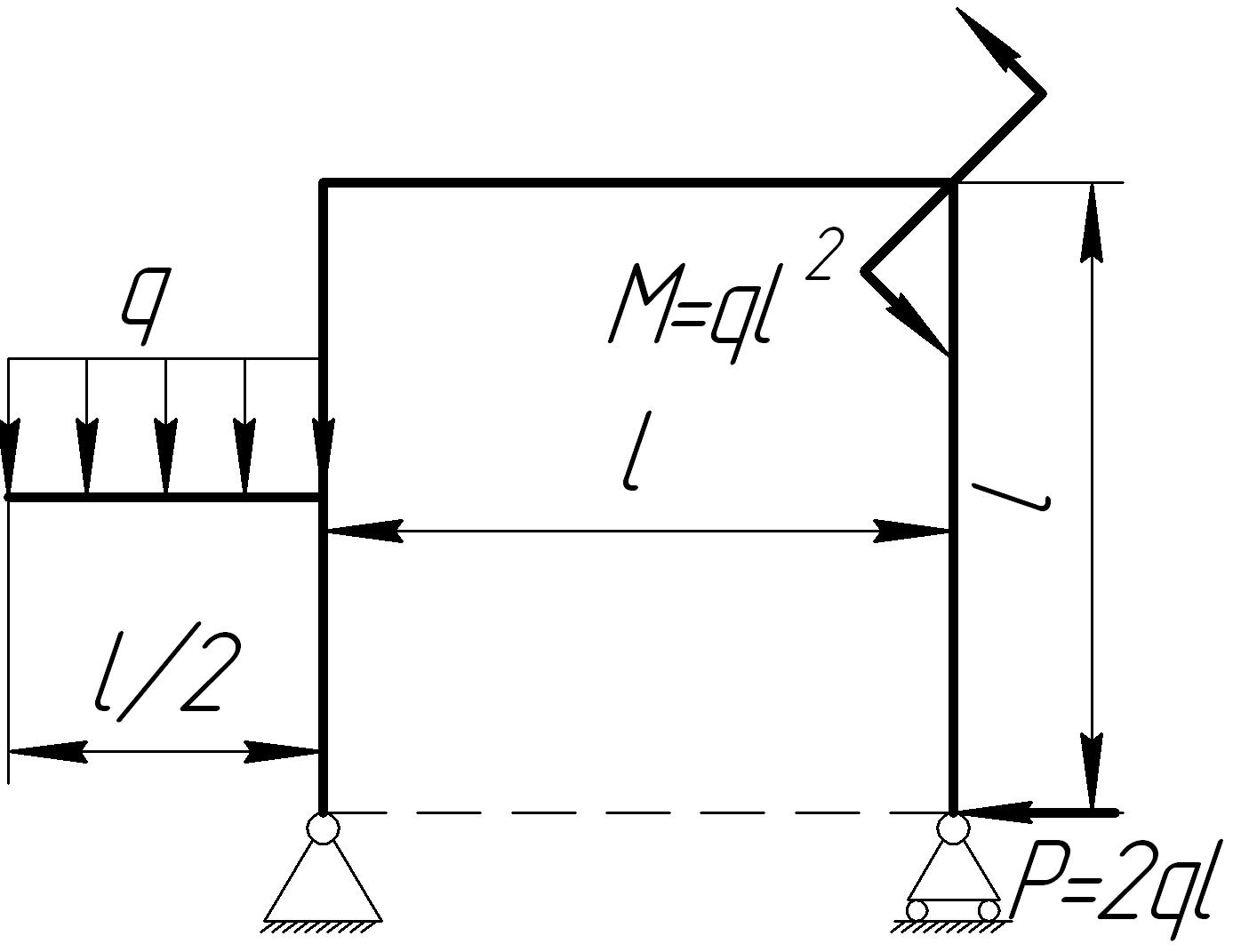
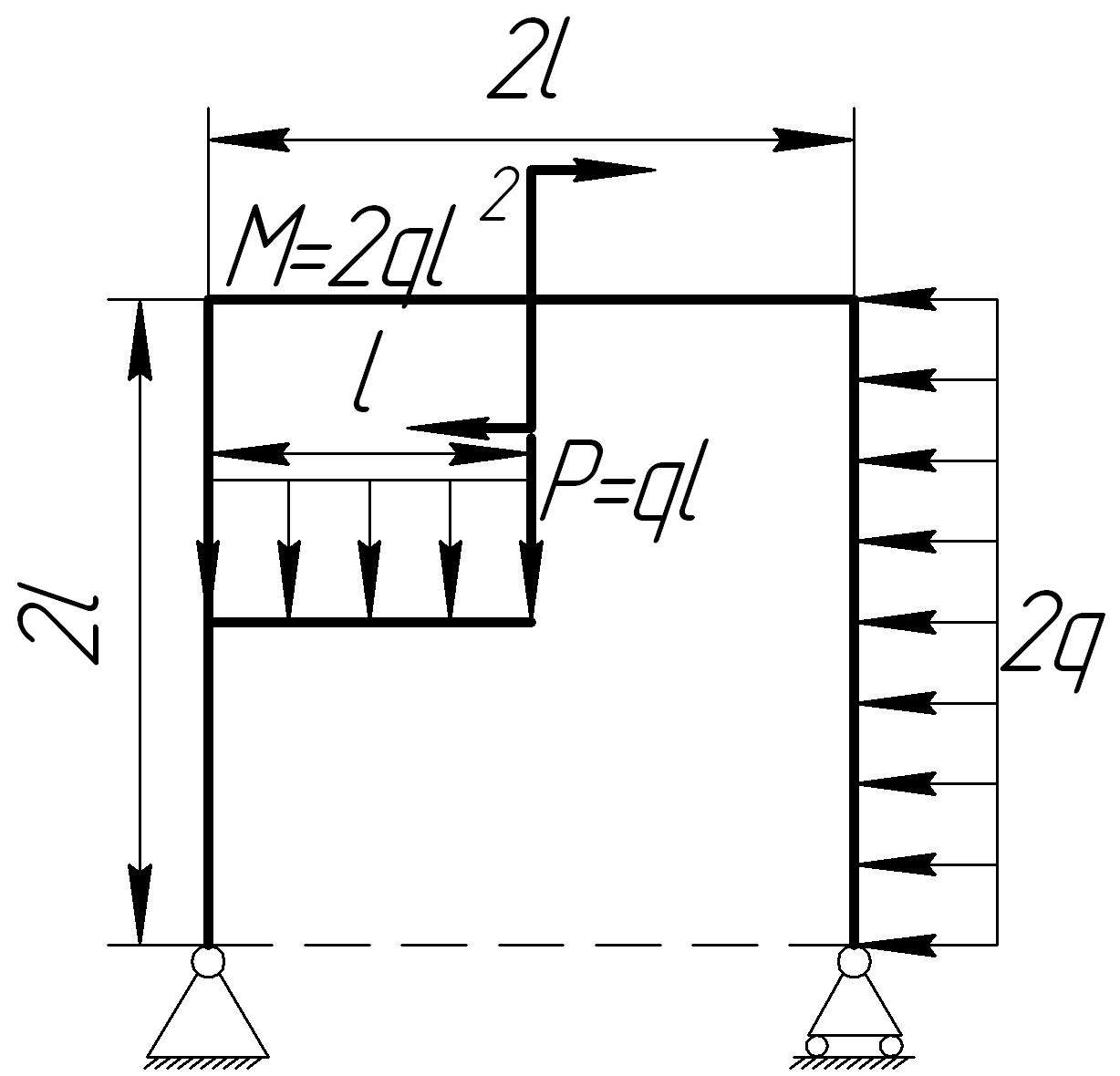
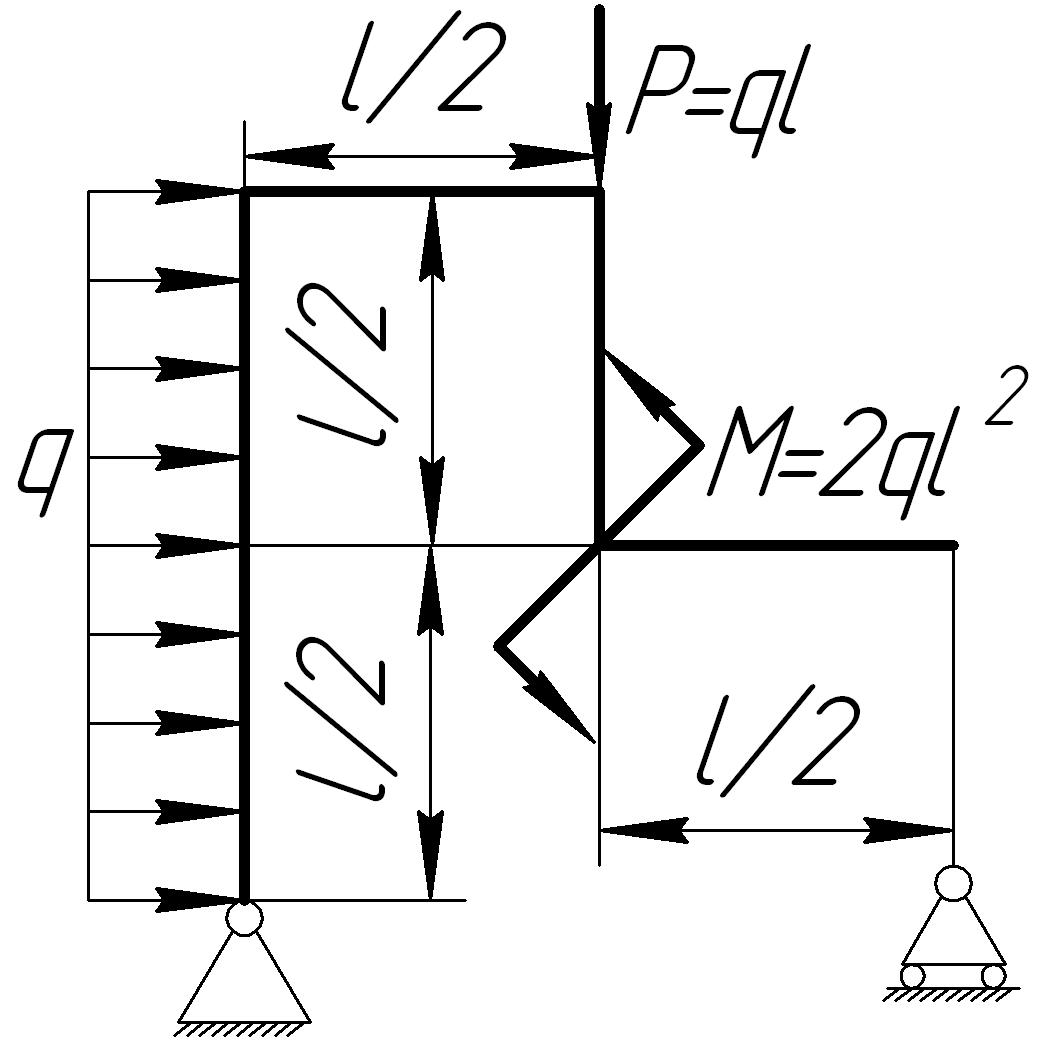
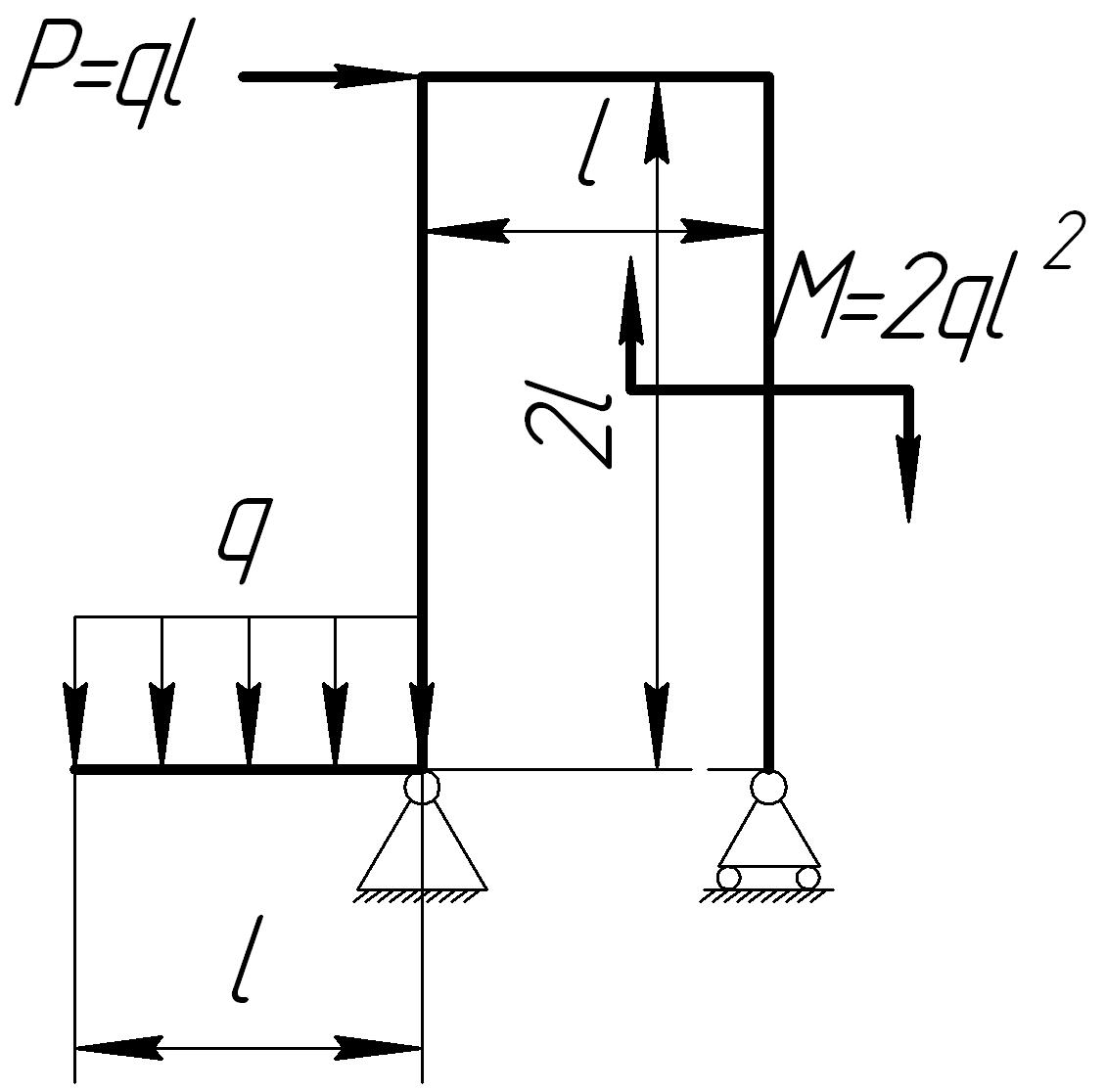
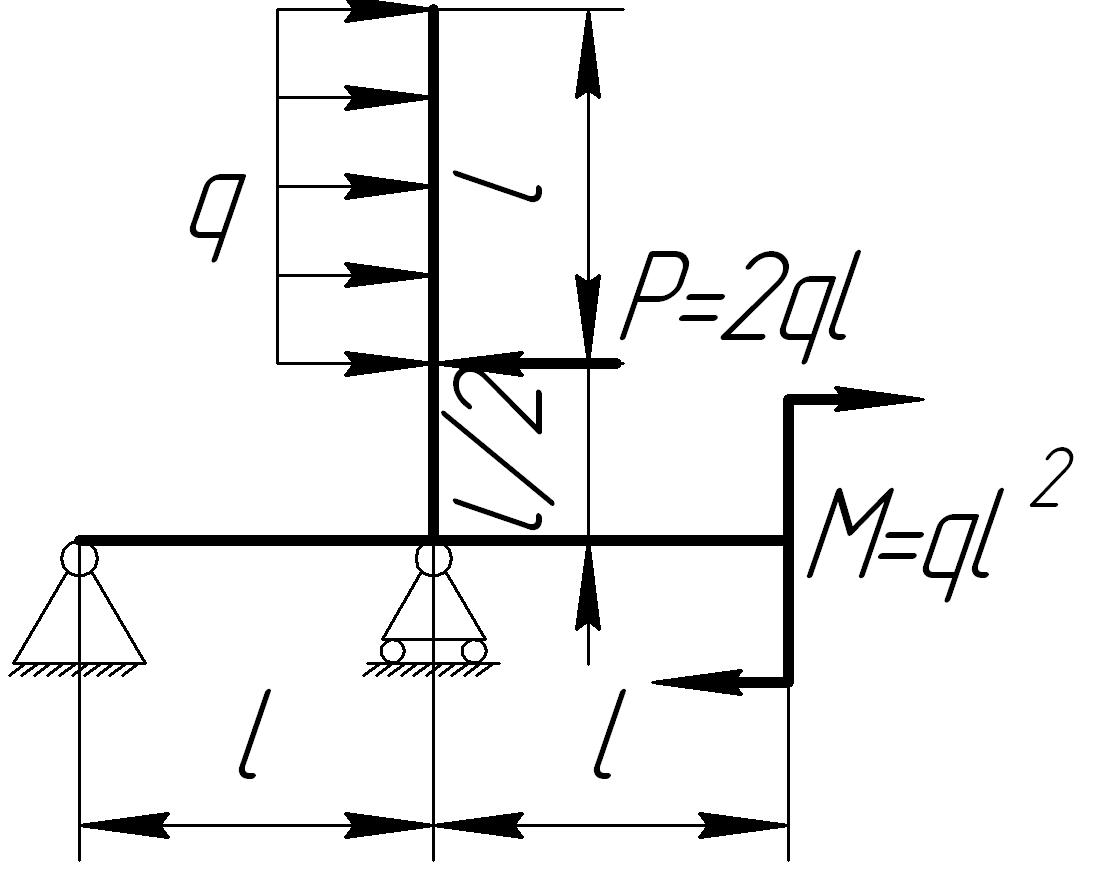
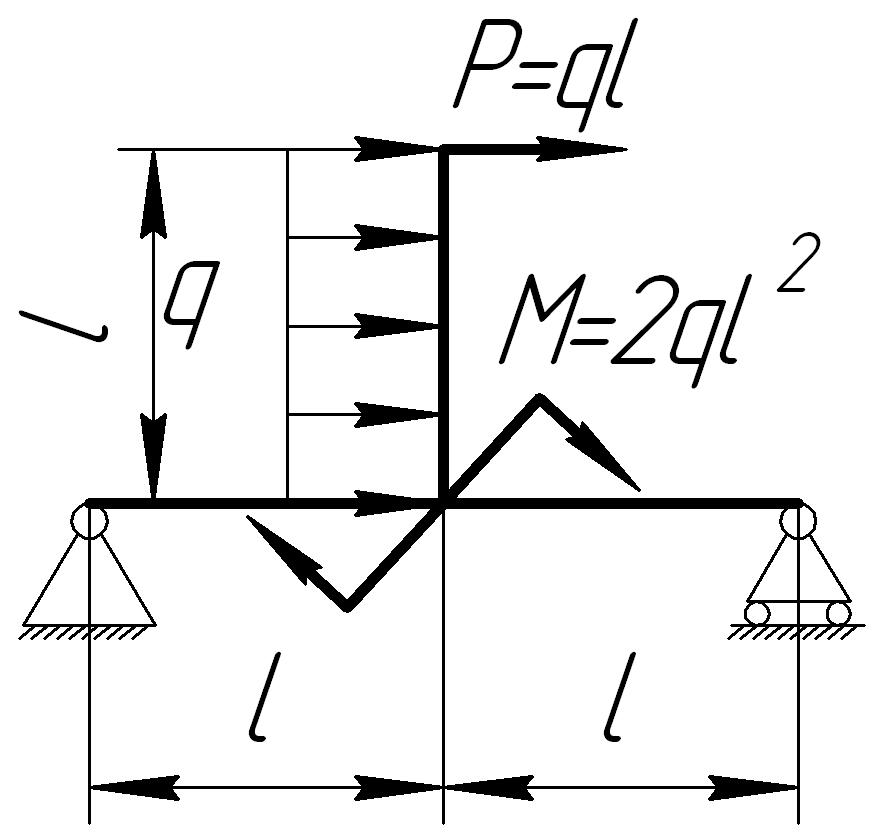
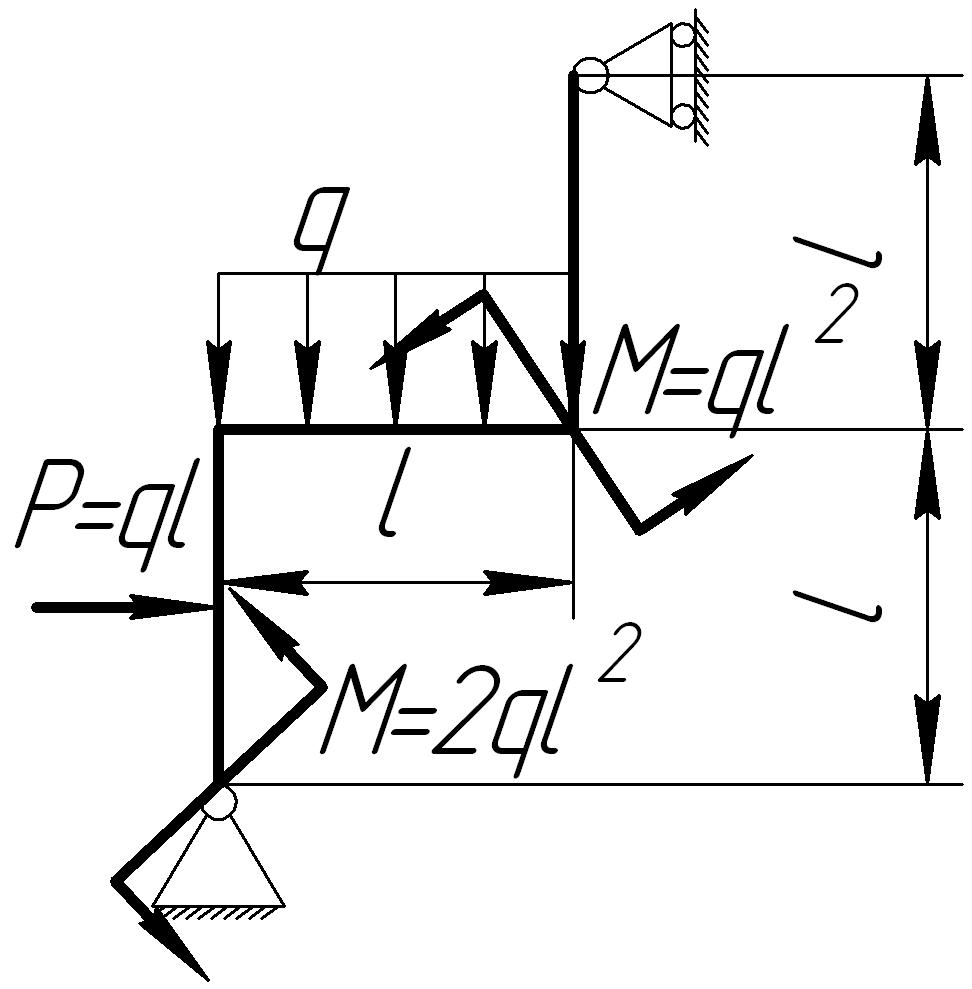
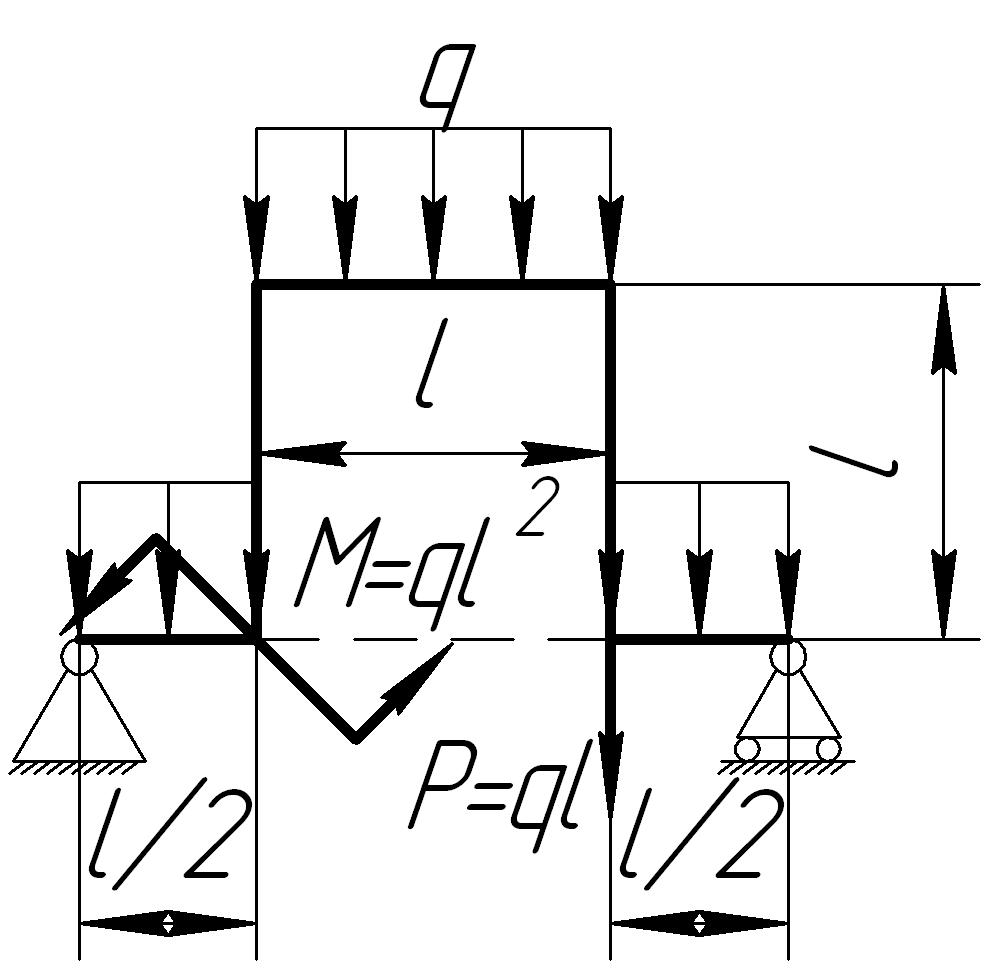
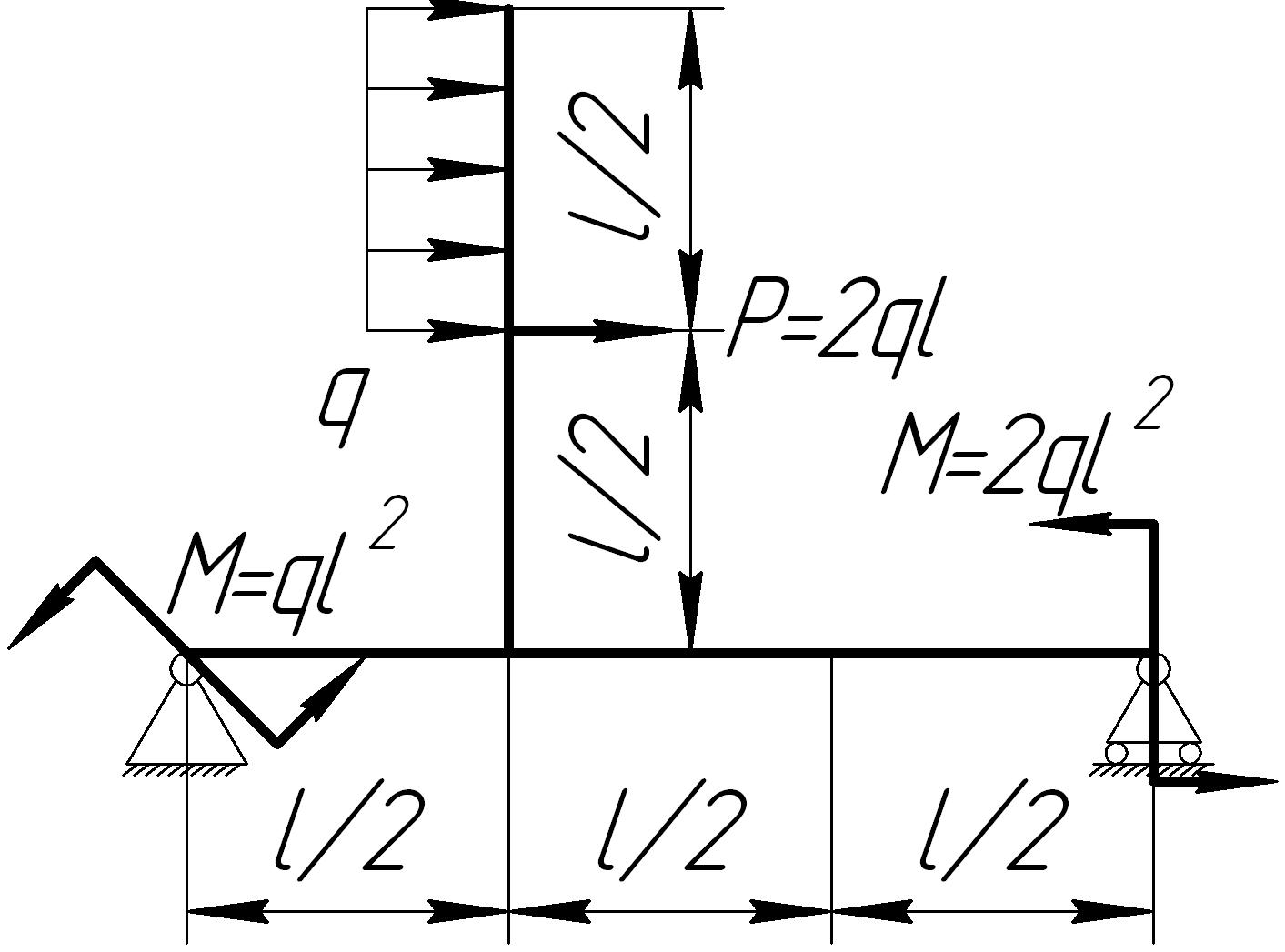
На основании исходных данных (рис. 6.9) построить эпюру внутренних силовых факторов в плоских рамах.
1. |
|
2. |
|
3. |
|
4. |
|
Рис. 6.9
5. |
|
6. |
|
7. |
|
8. |
|
9. |
|
10. |
|
11. |
|
12. |
|
Рис. 6.9
13. |
|
14. |
|
15. |
|
16. |
|
17. |
|
18. |
|
19. |
|
20 |
|
Рис. 6.9
21. |
|
22. |
|
23. |
|
24. |
|
25. |
|
26. |
|
27. |
|
28. |
|
29. |
|
30. |
|
Рис. 6.9
Задача 10
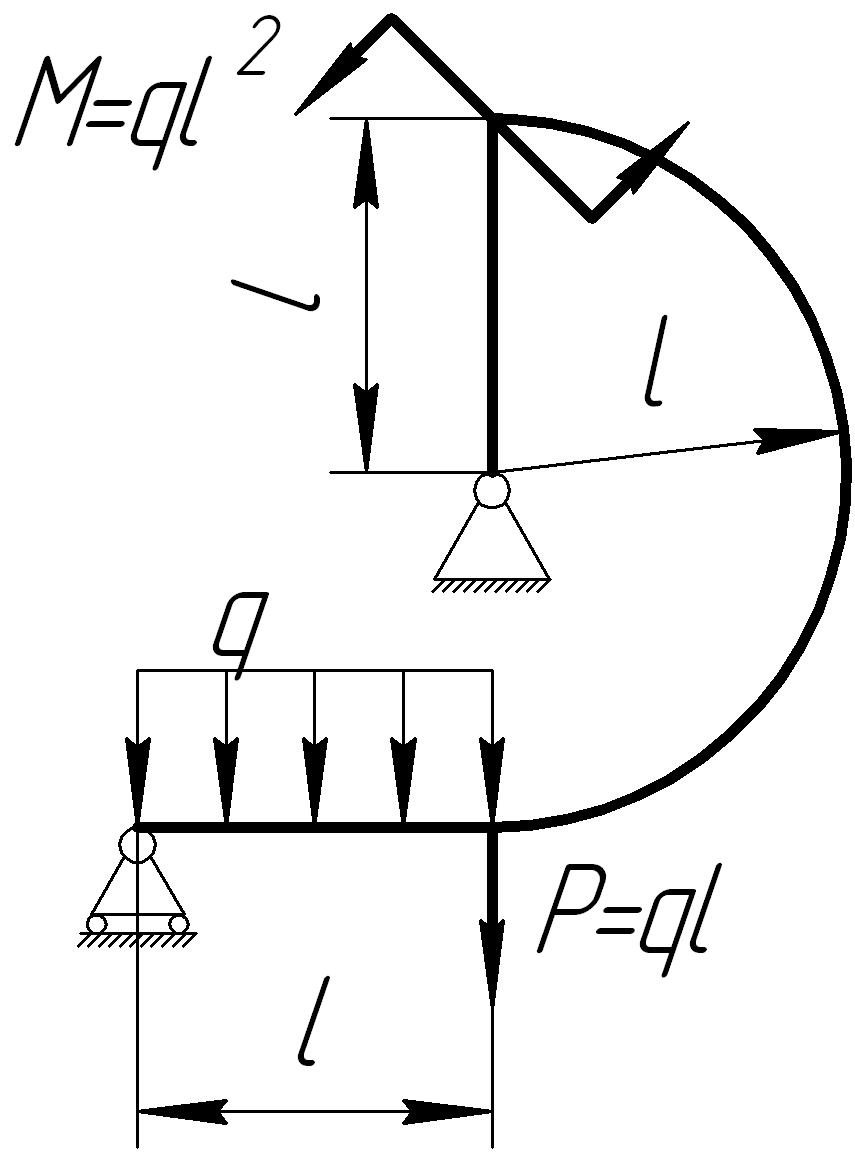
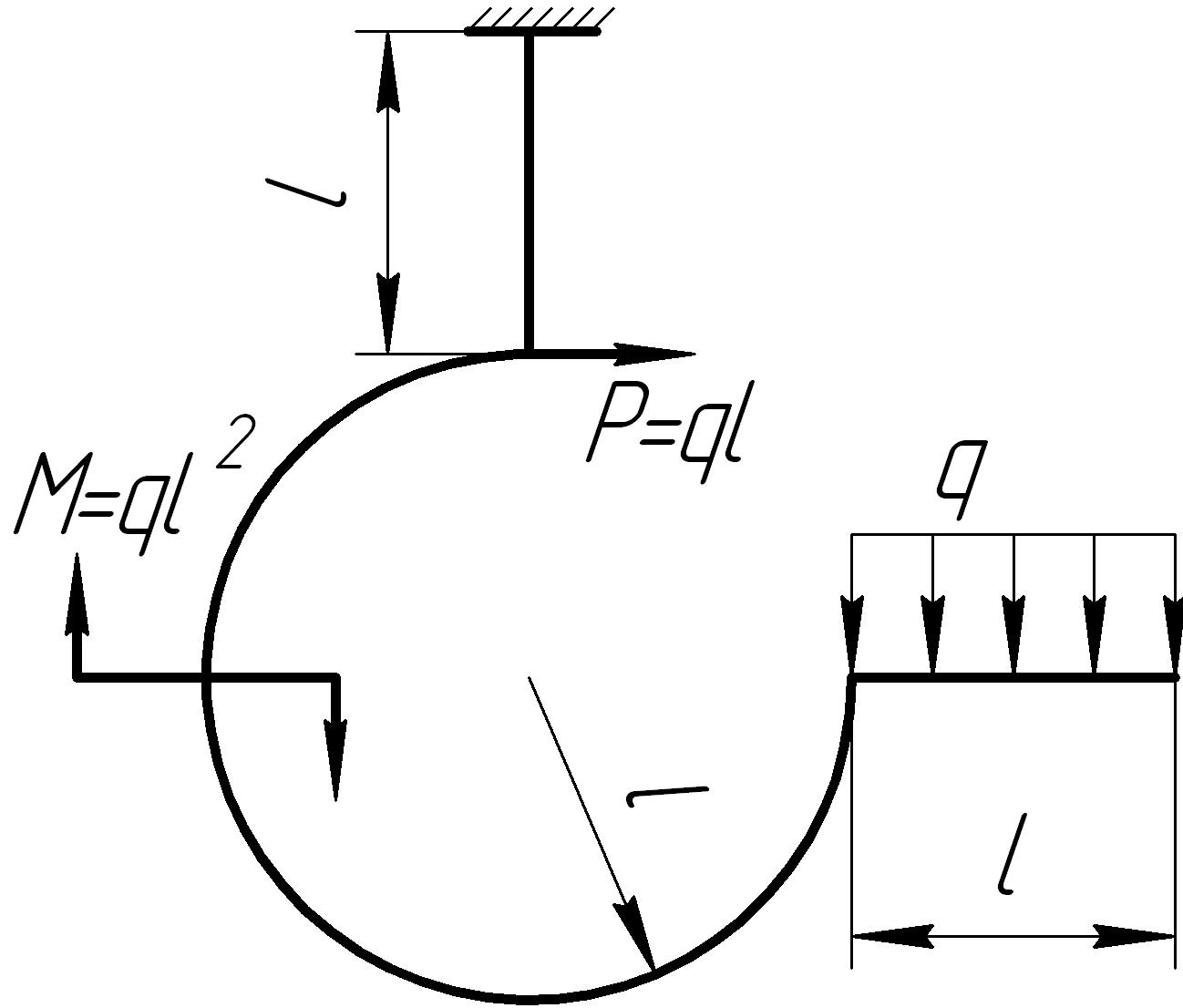
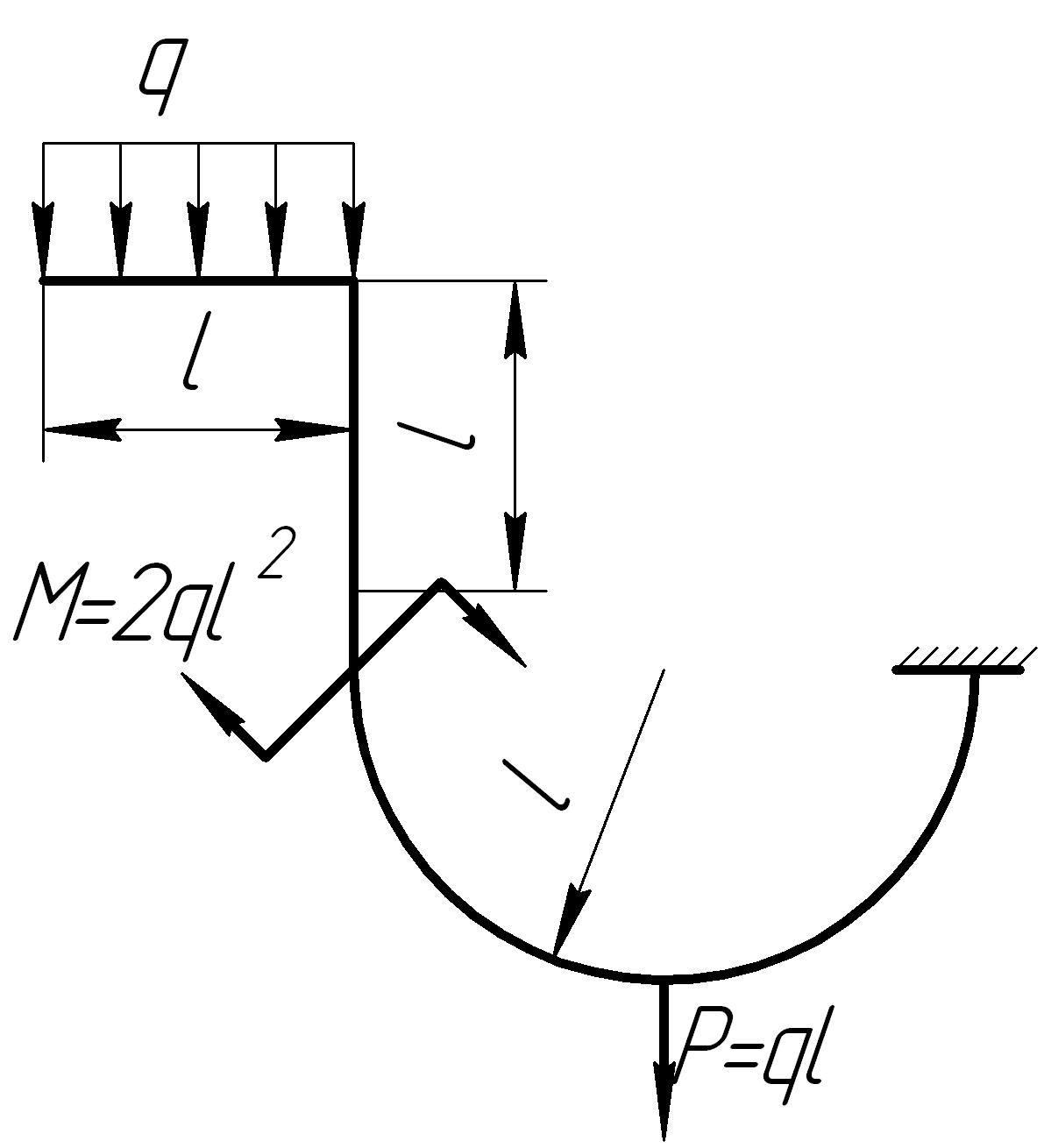
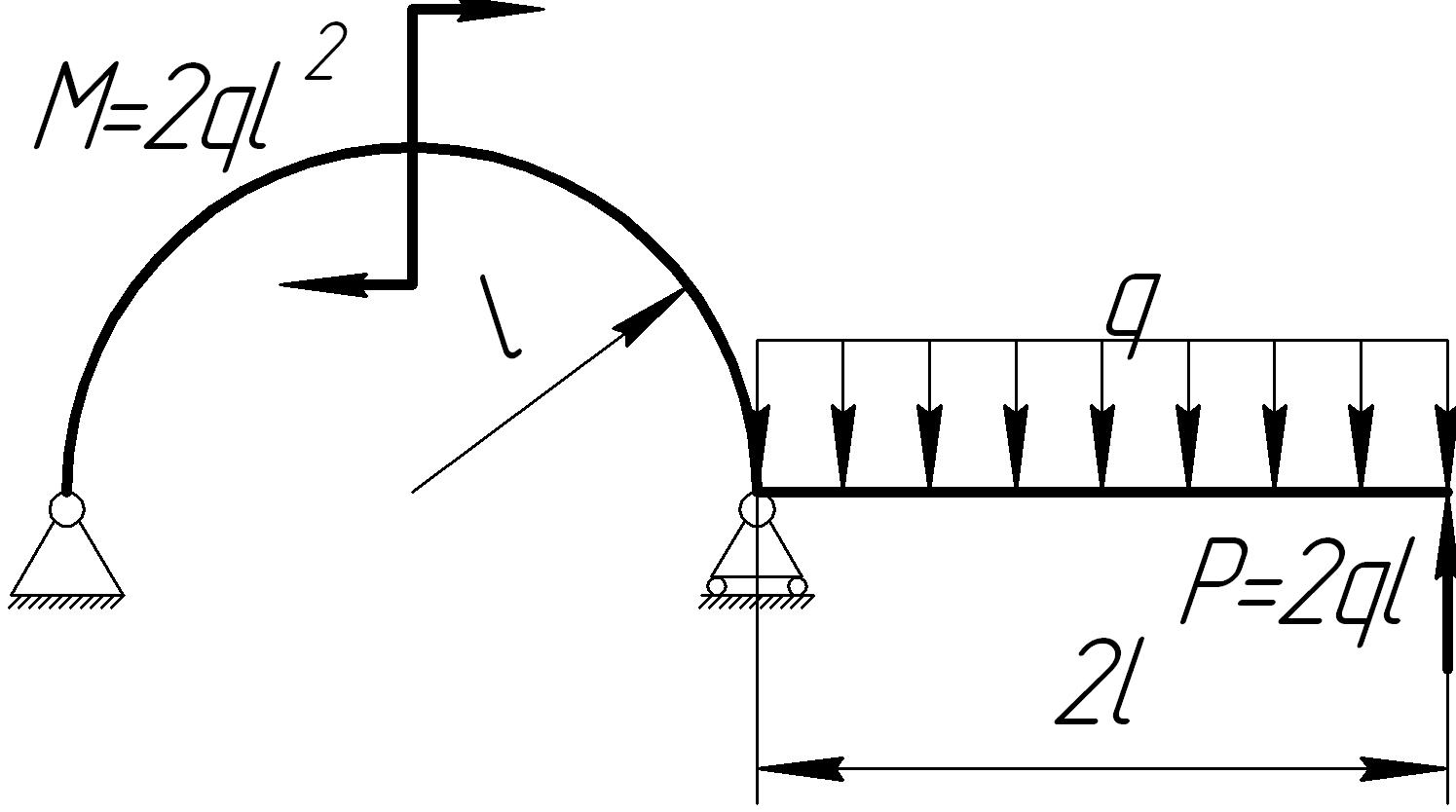
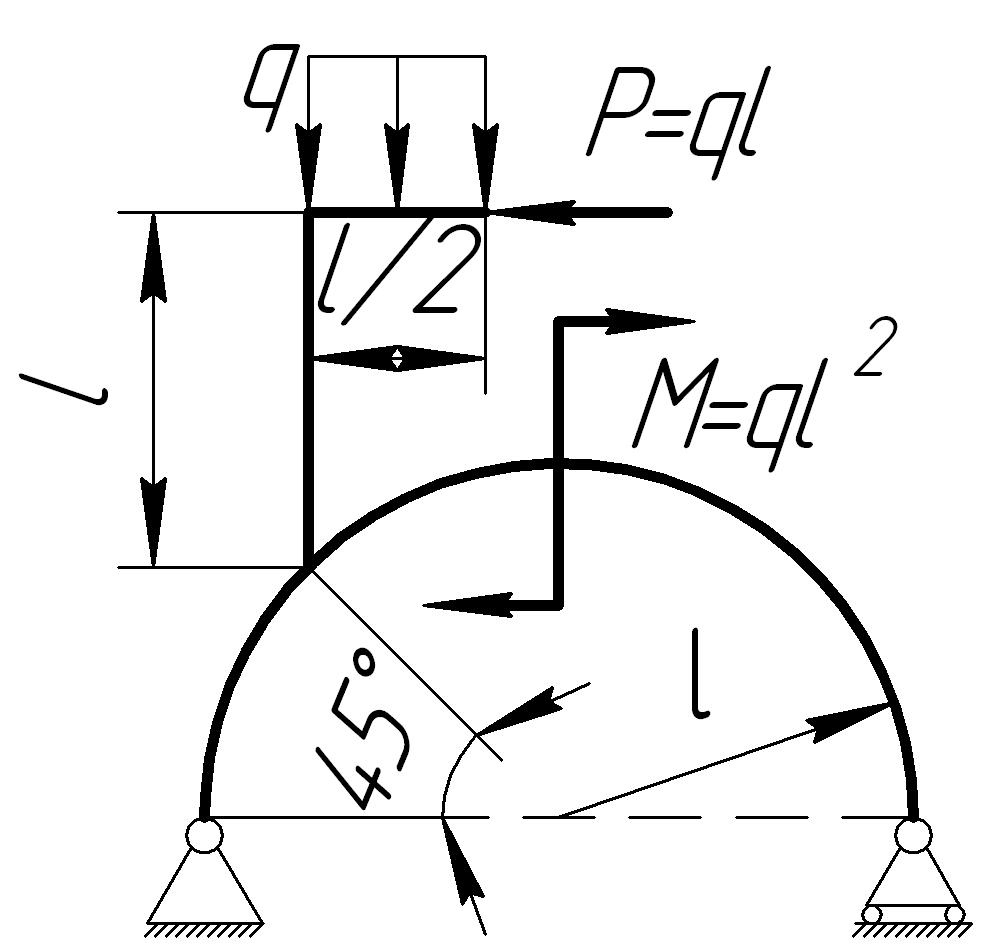
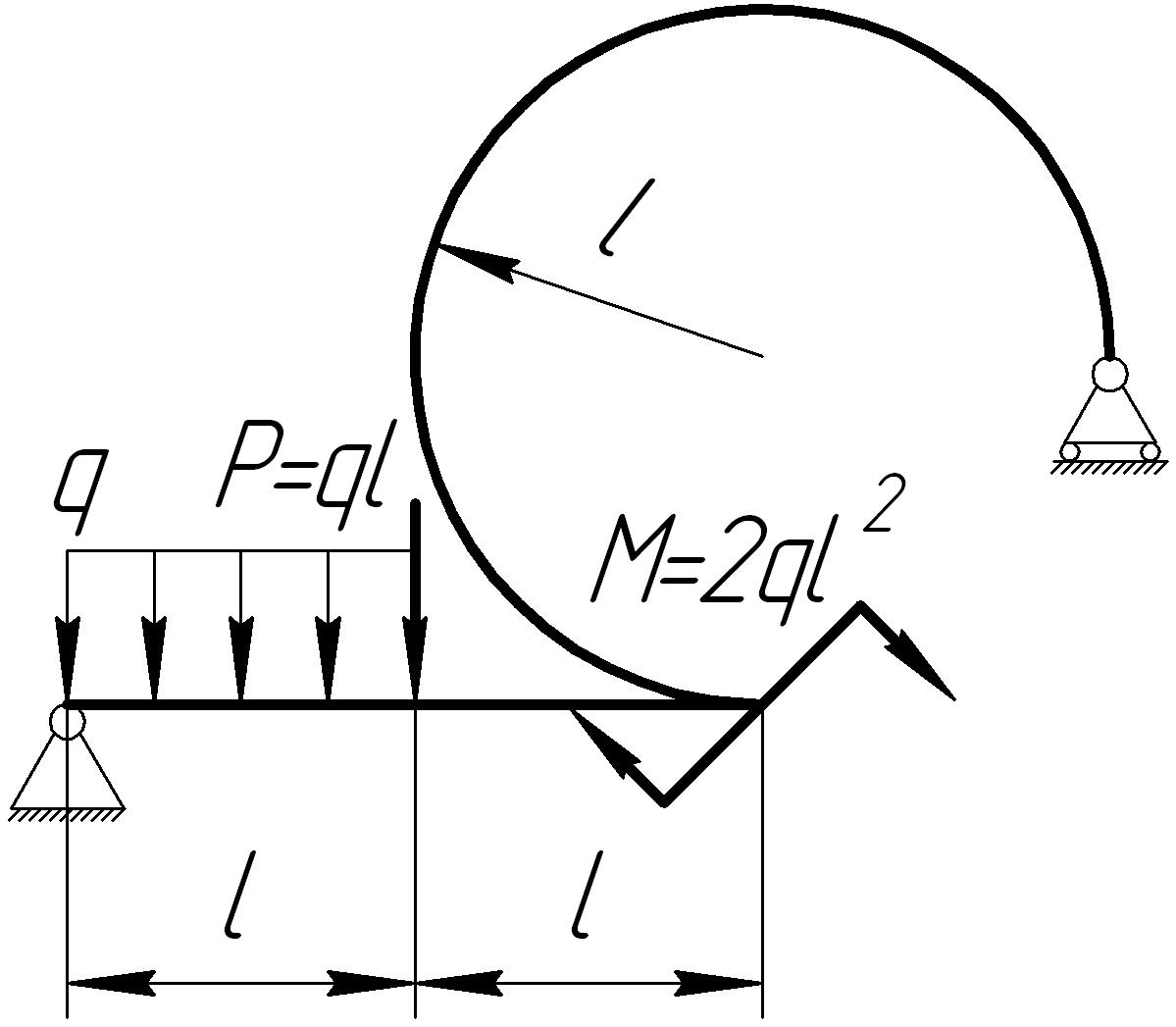
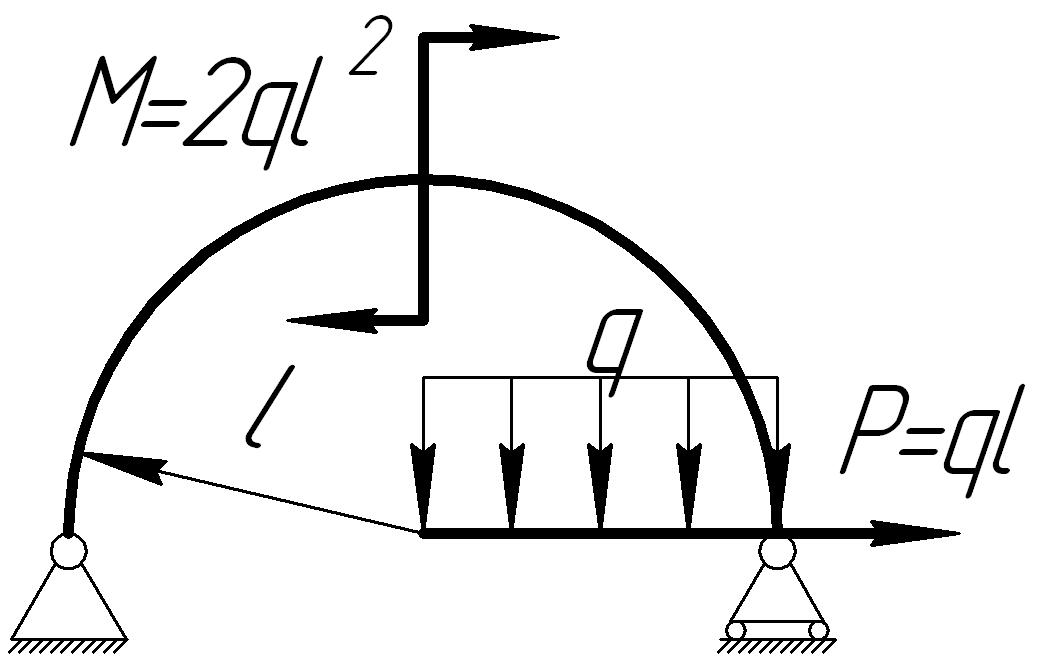
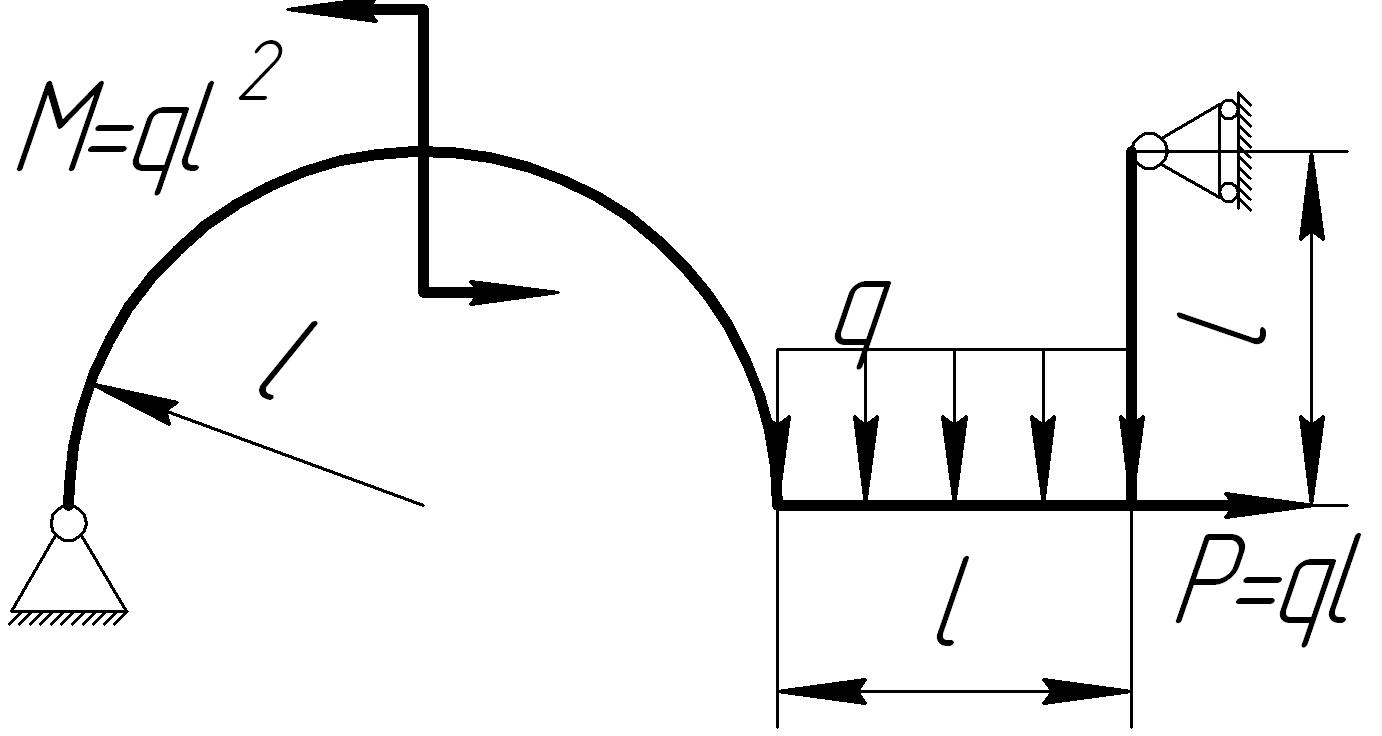
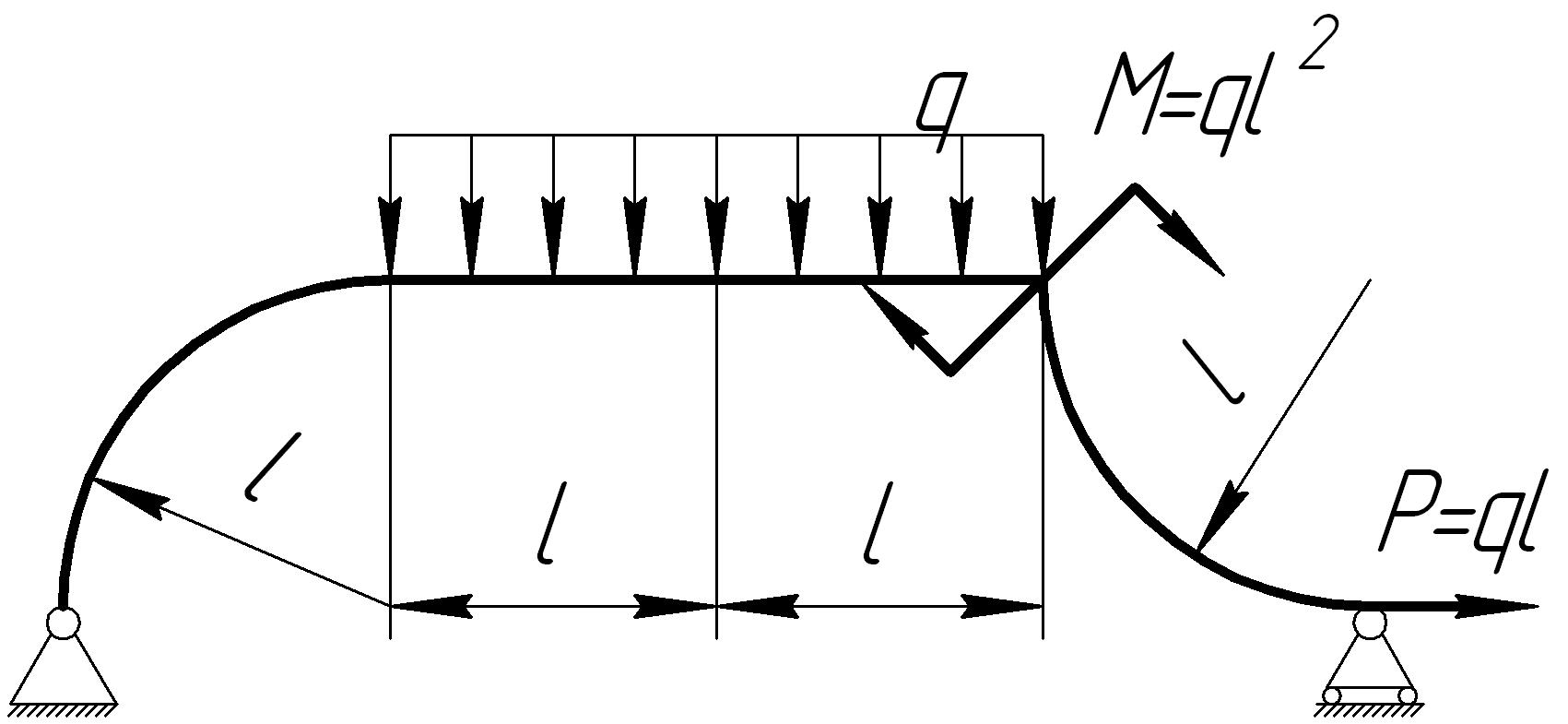
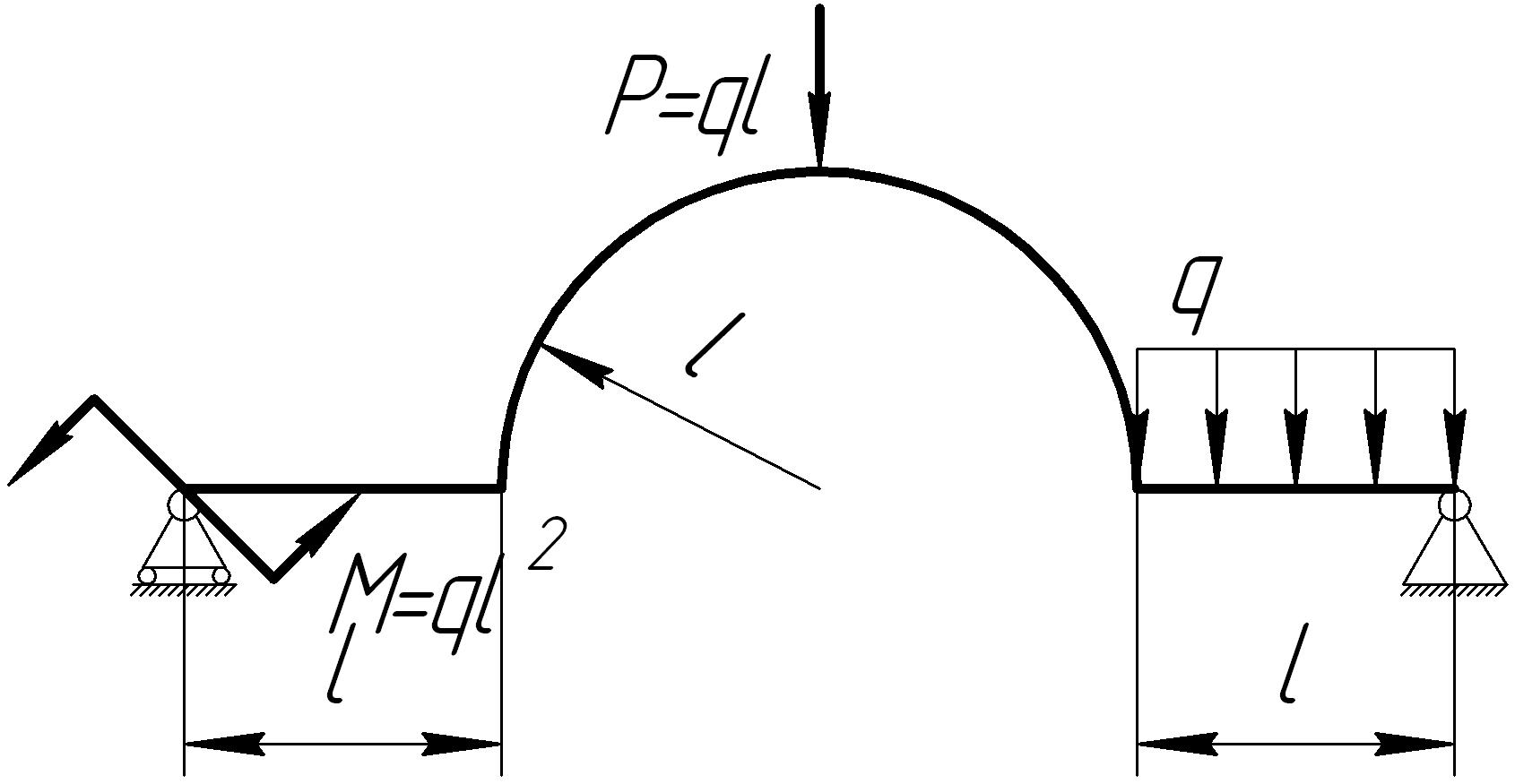
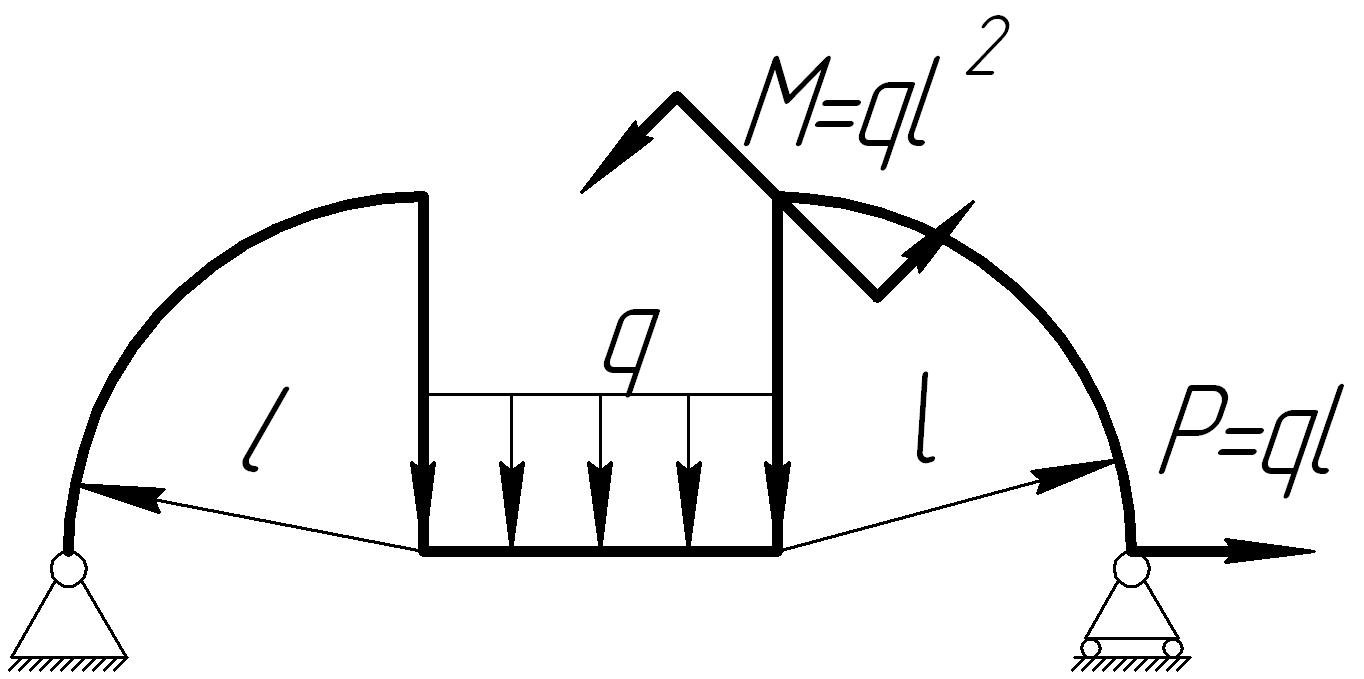
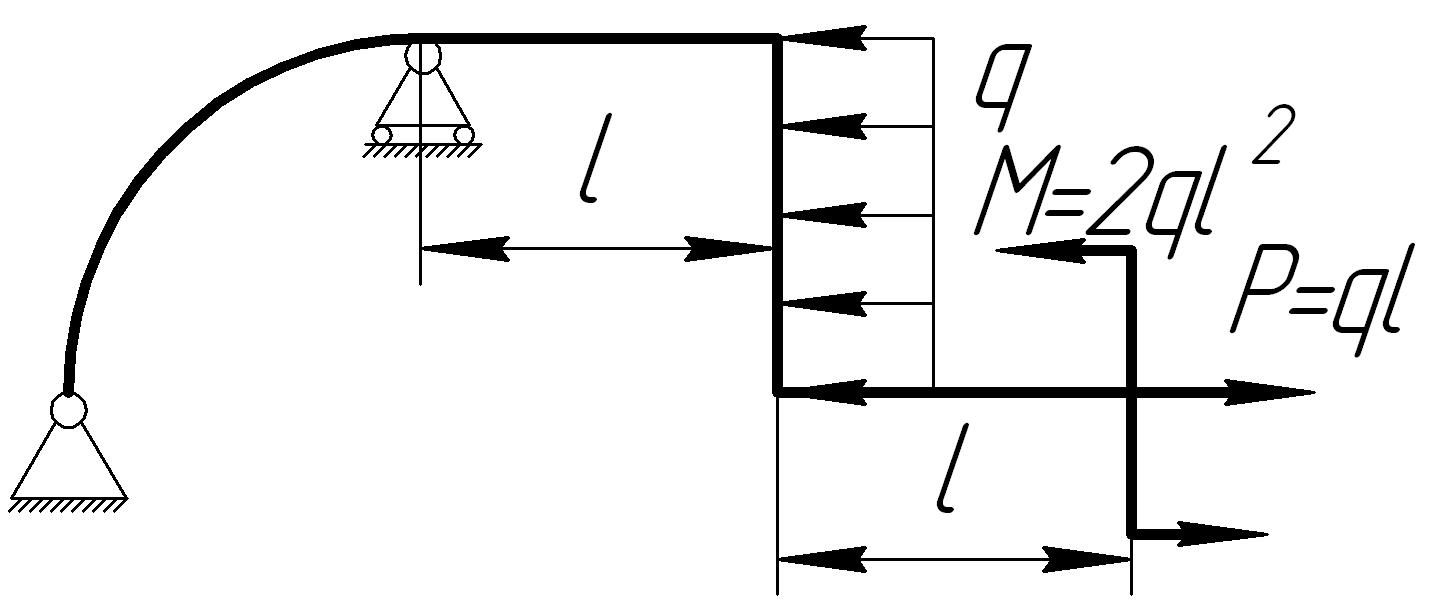
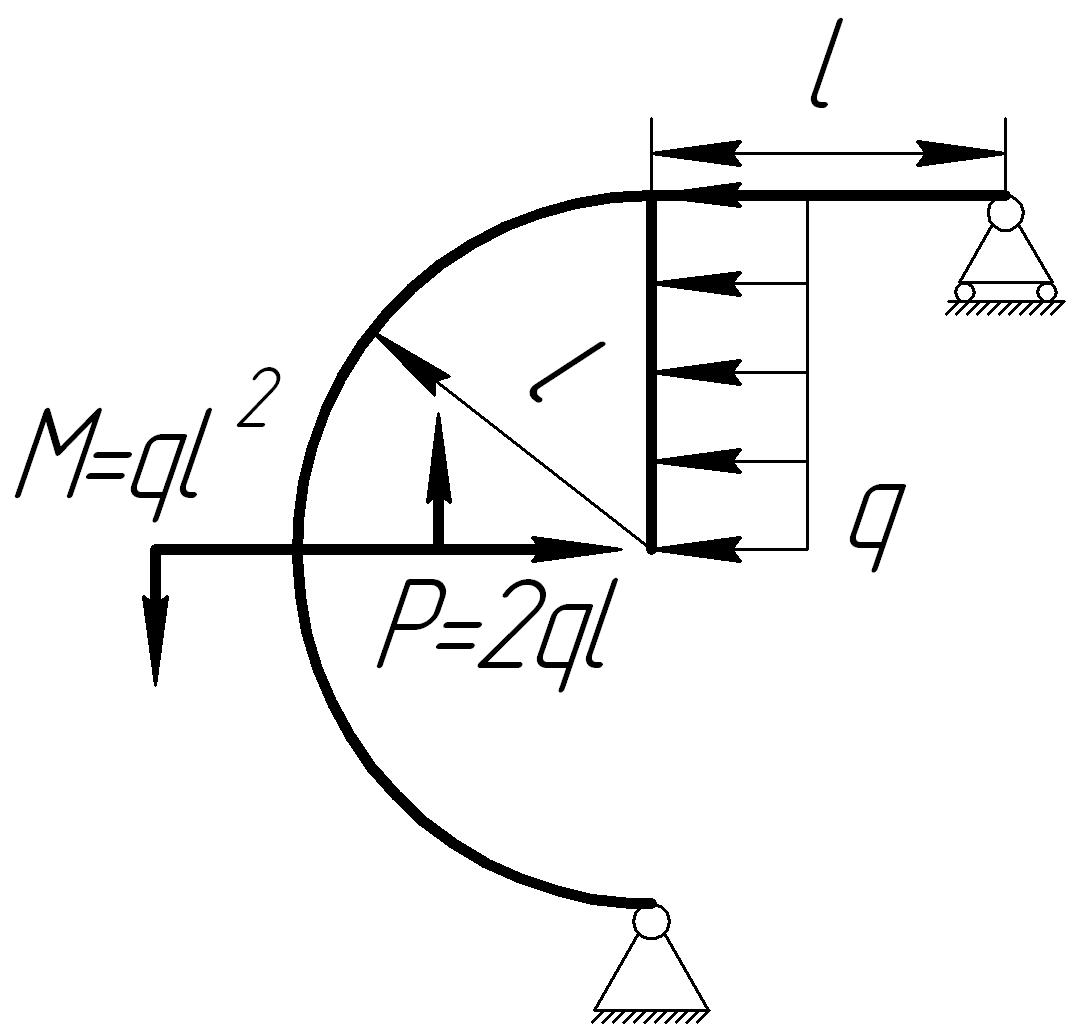
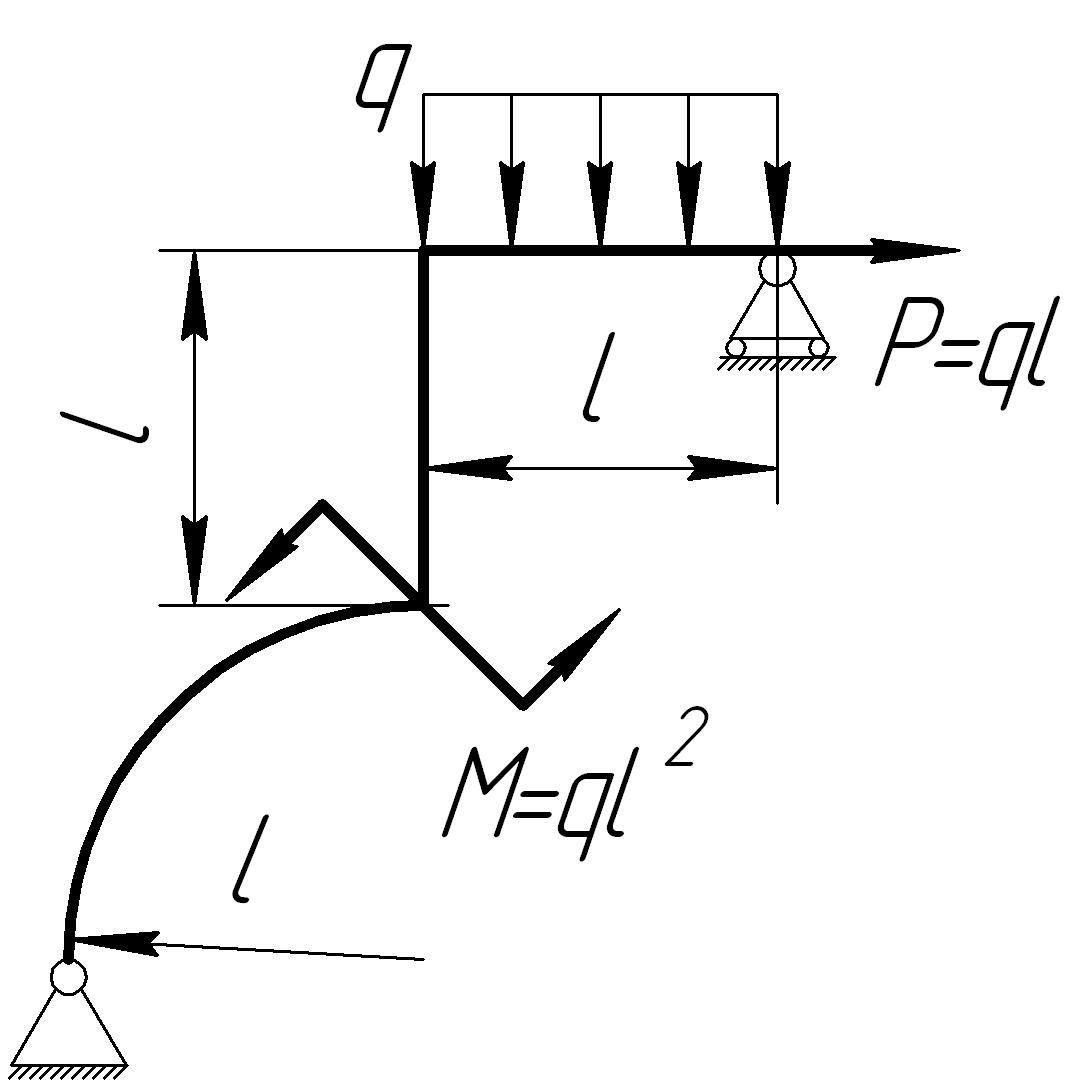
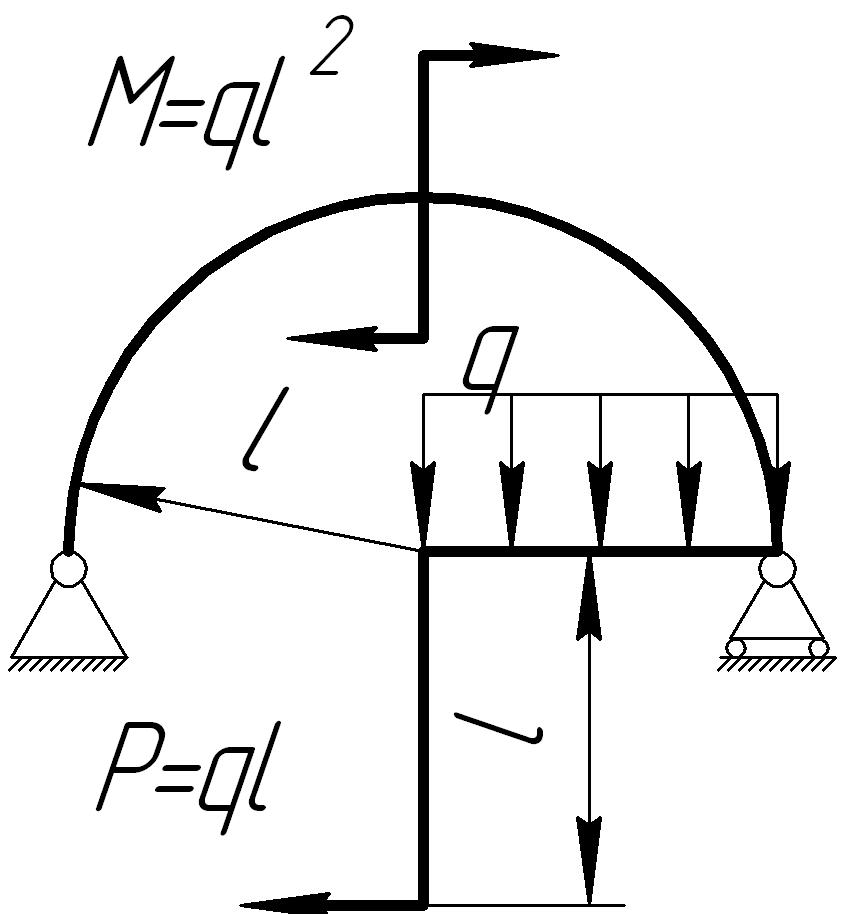
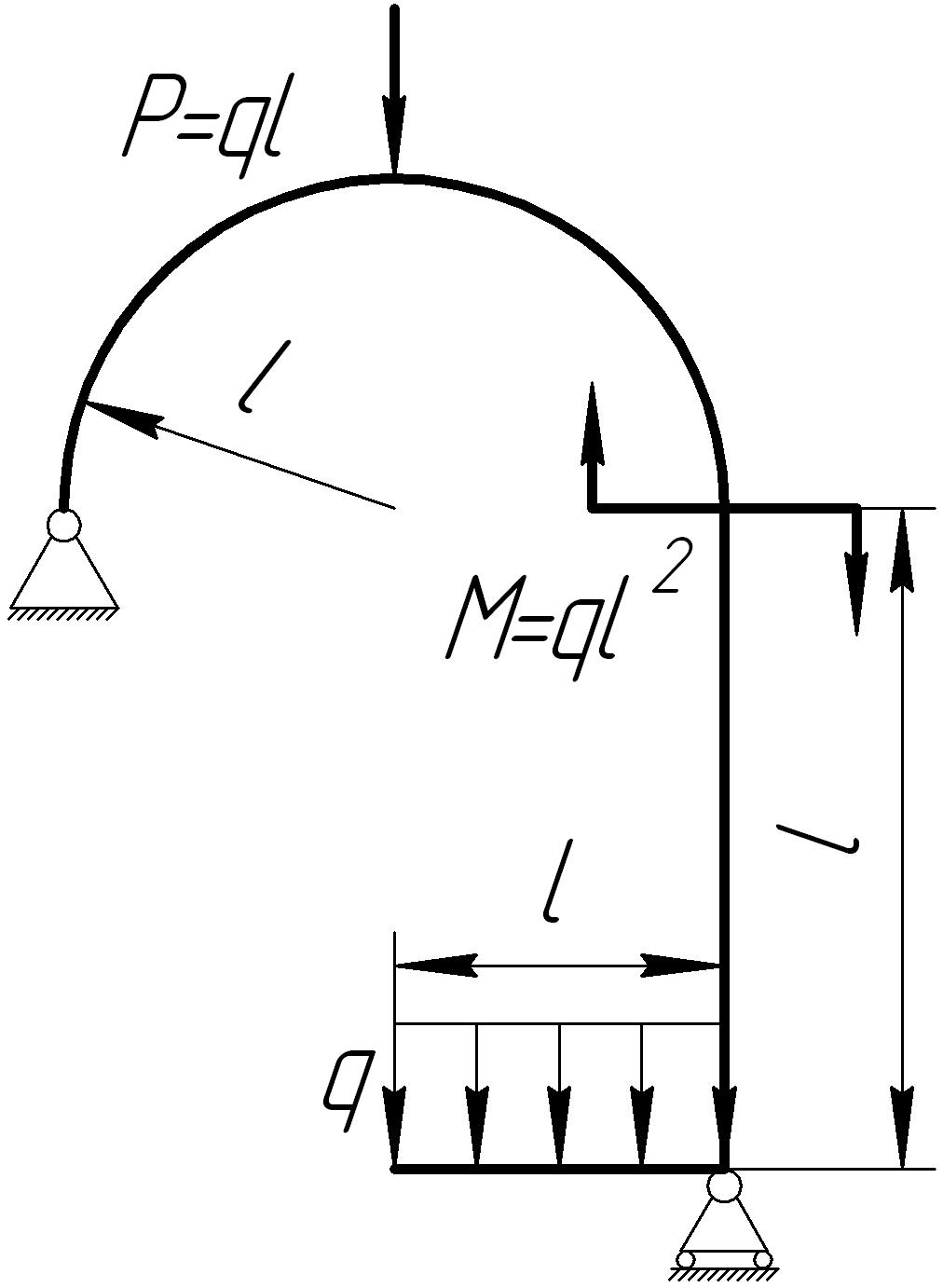
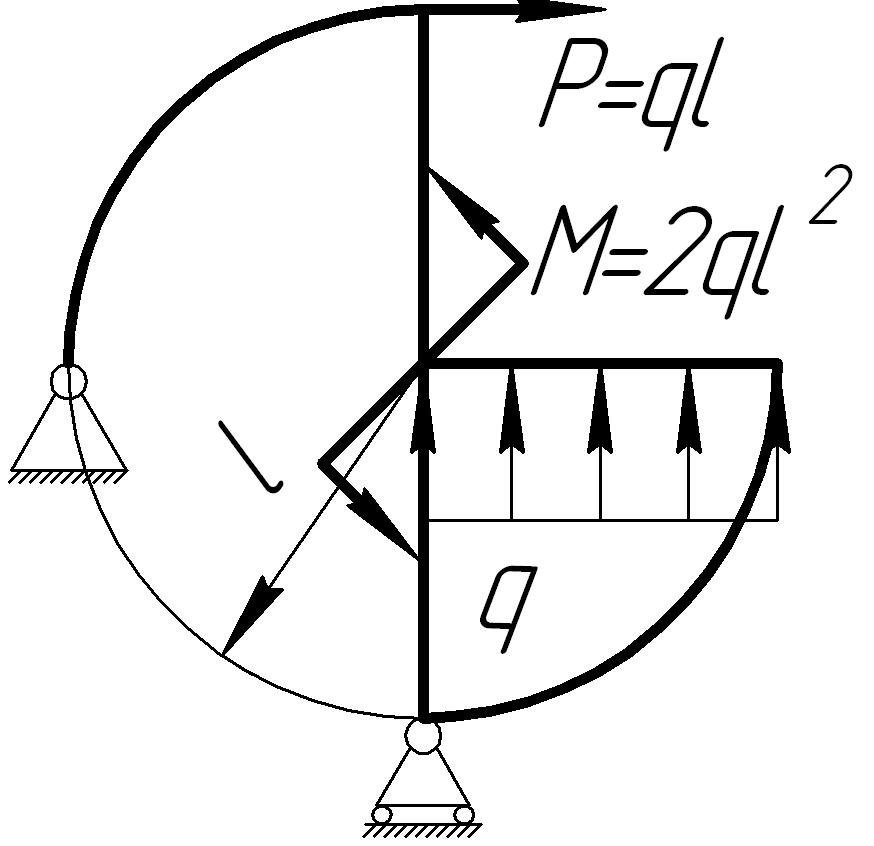
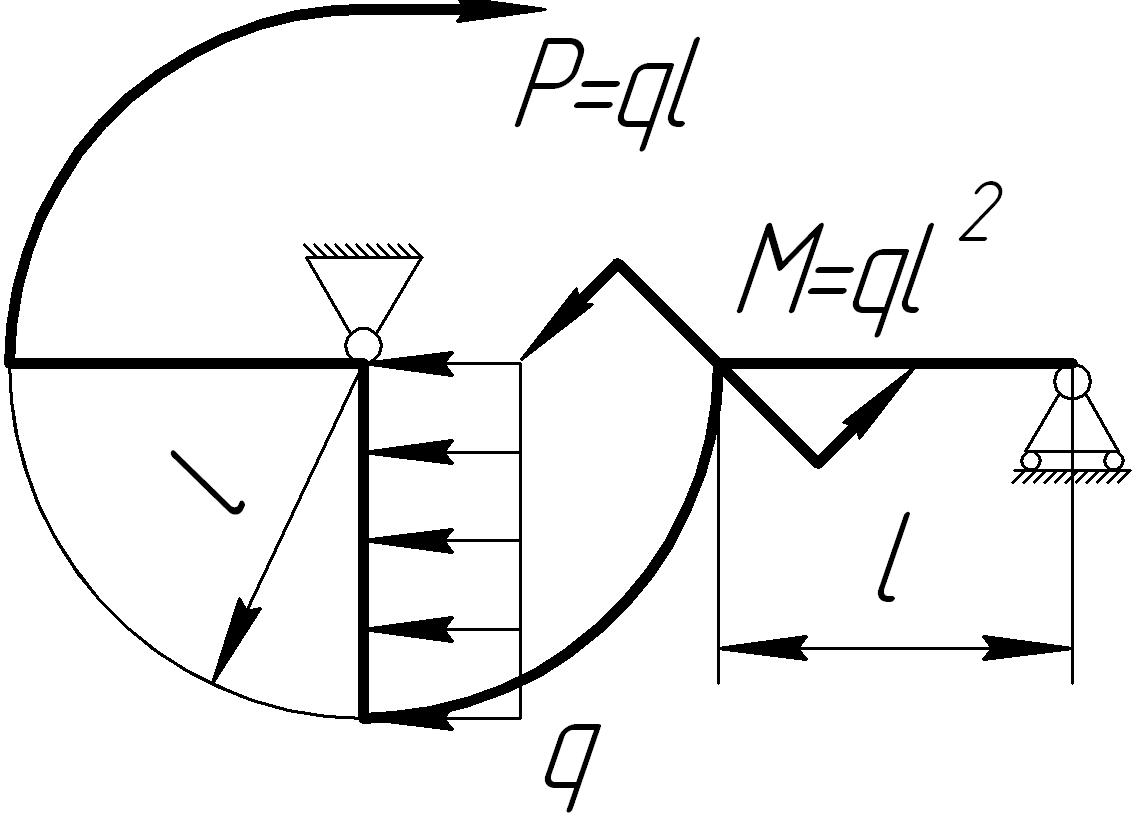
На основании исходных данных (рис. 6.10) построить эпюры внутренних силовых факторов в кривых брусьях.
1. |
|
2. |
|
3. |
|
4. |
|
Рис. 6.10
5. |
|
6. |
|
7. |
|
8. |
|
9. |
|
10. |
|
Рис. 6.10
11. |
|
12. |
|
13. |
|
14. |
|
15. |
|
16. |
|
Рис. 6.10
17. |
|
18. |
|
19. |
|
20. |
|
21. |
|
22. |
|
Рис. 6.10
23. |
|
24. |
|
25. |
|
26. |
|
27. |
|
28. |
|
Рис. 6.10
29. |
|
30. |
|
Рис. 6.10
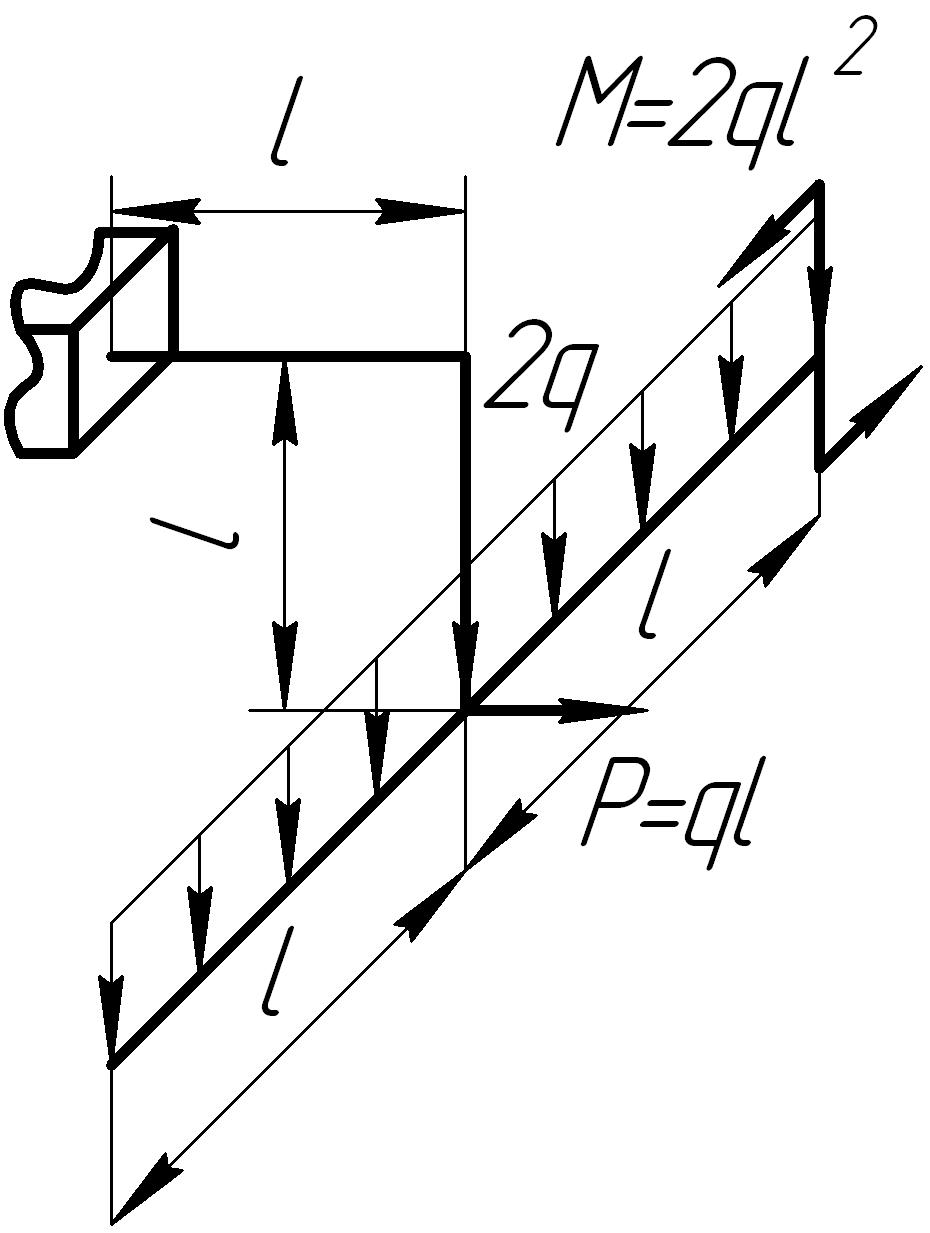
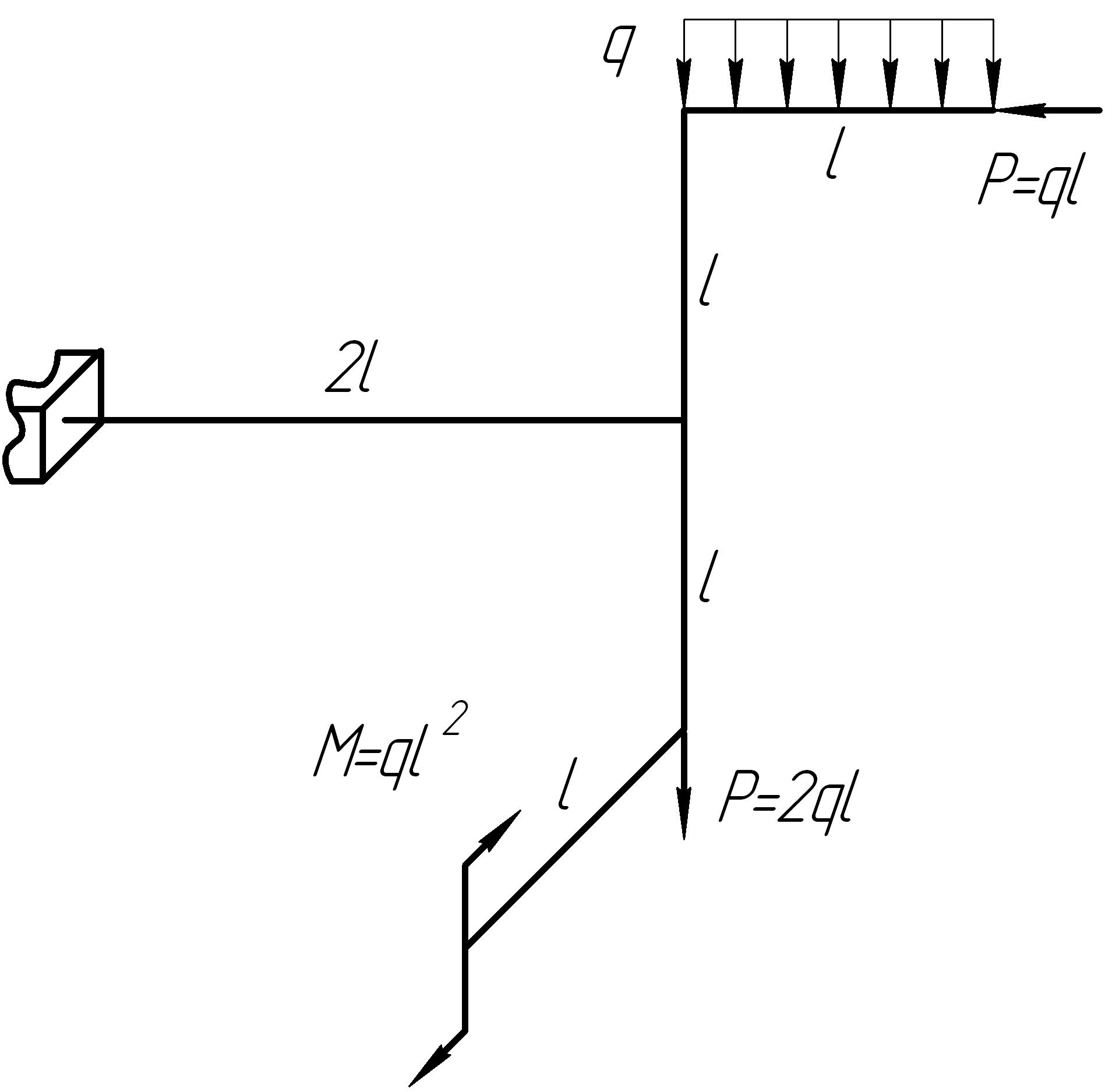
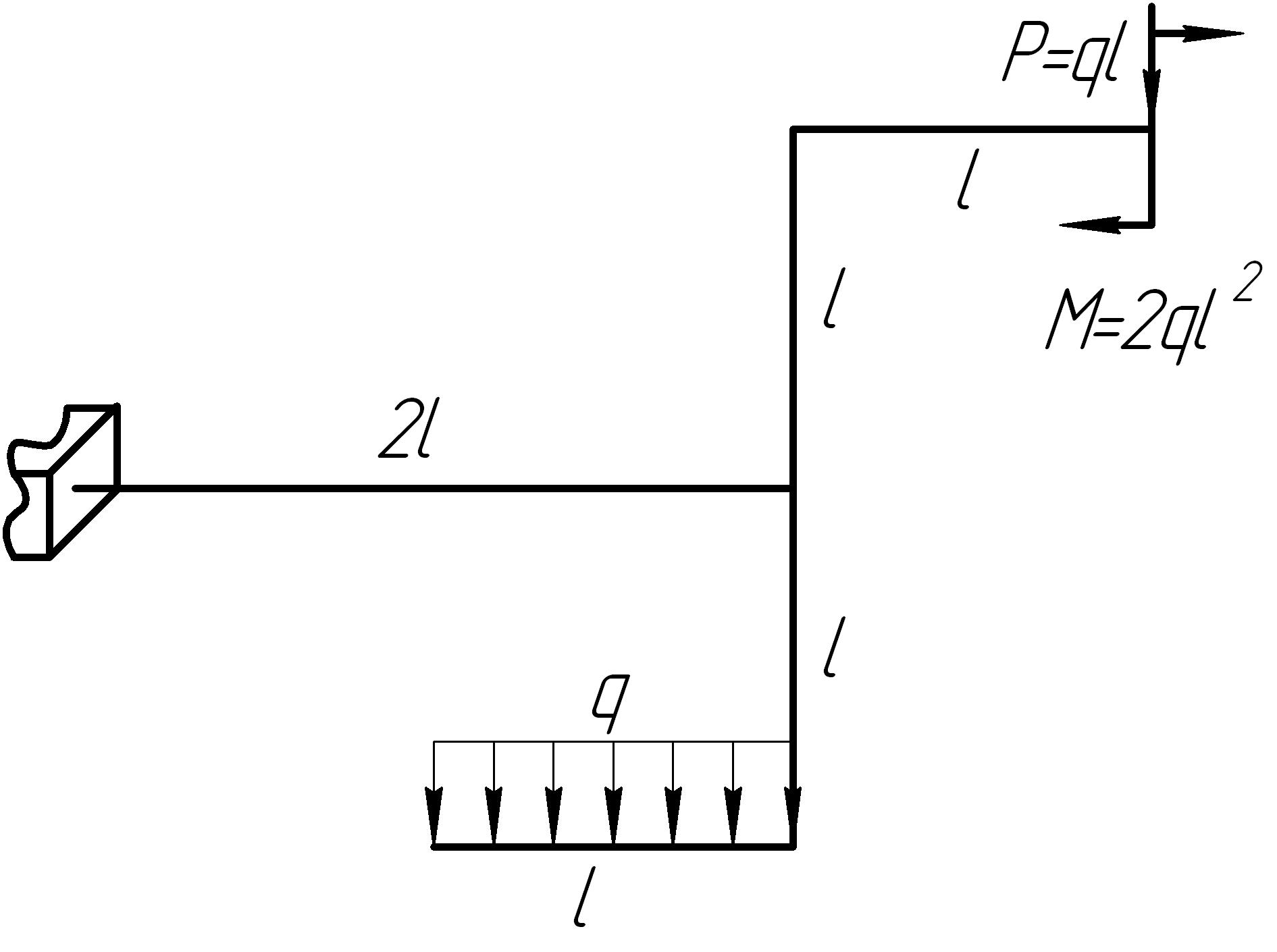
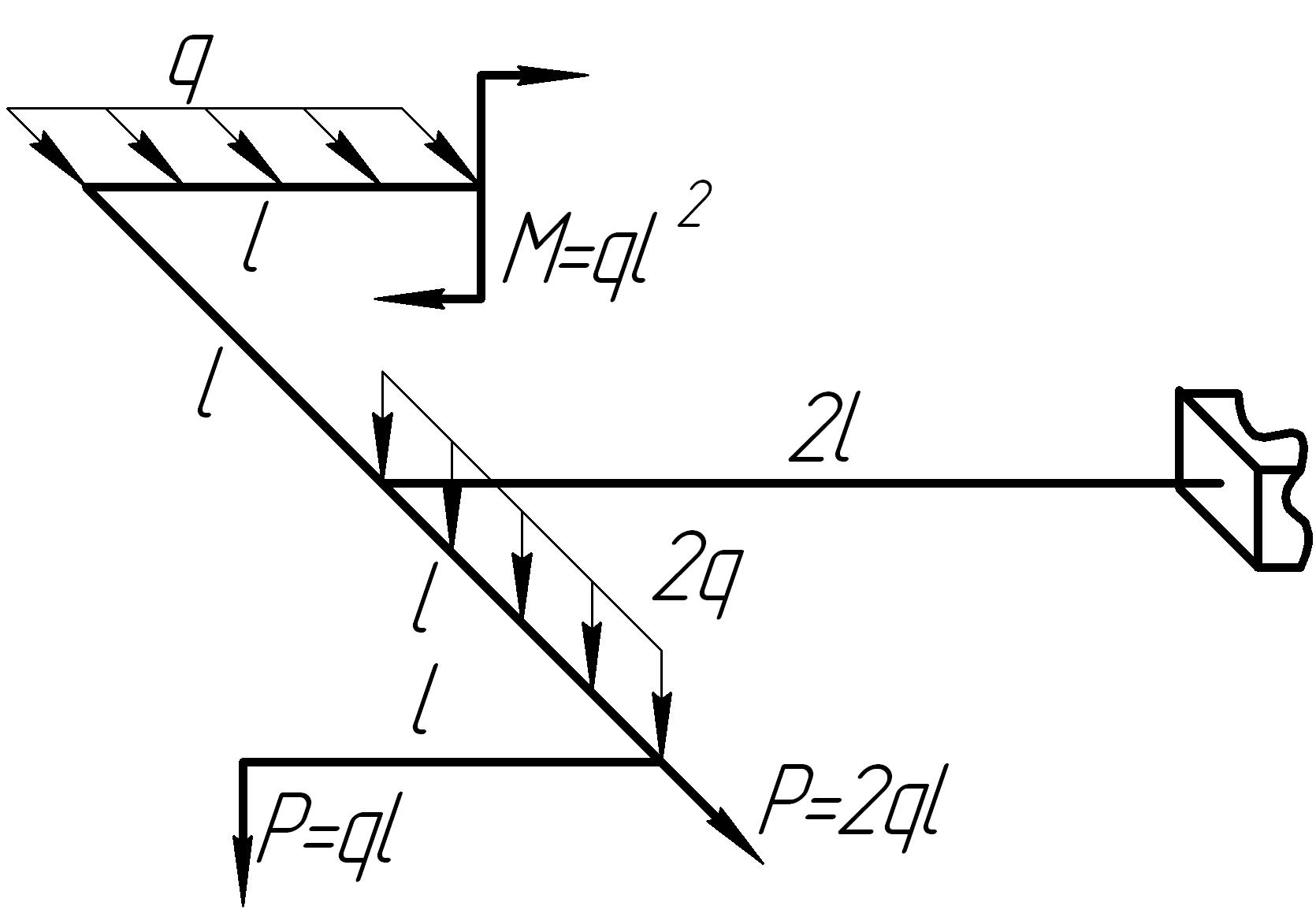
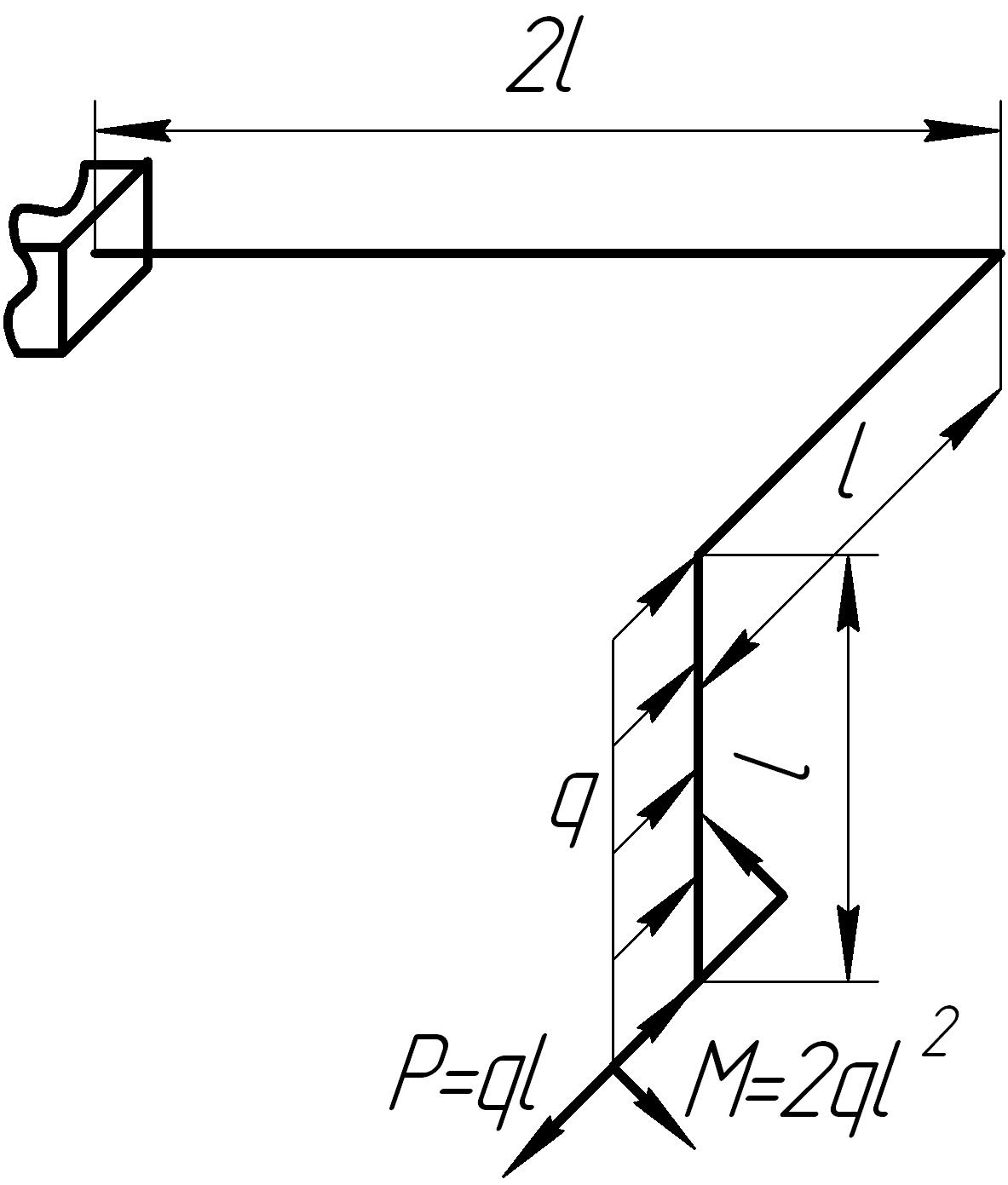
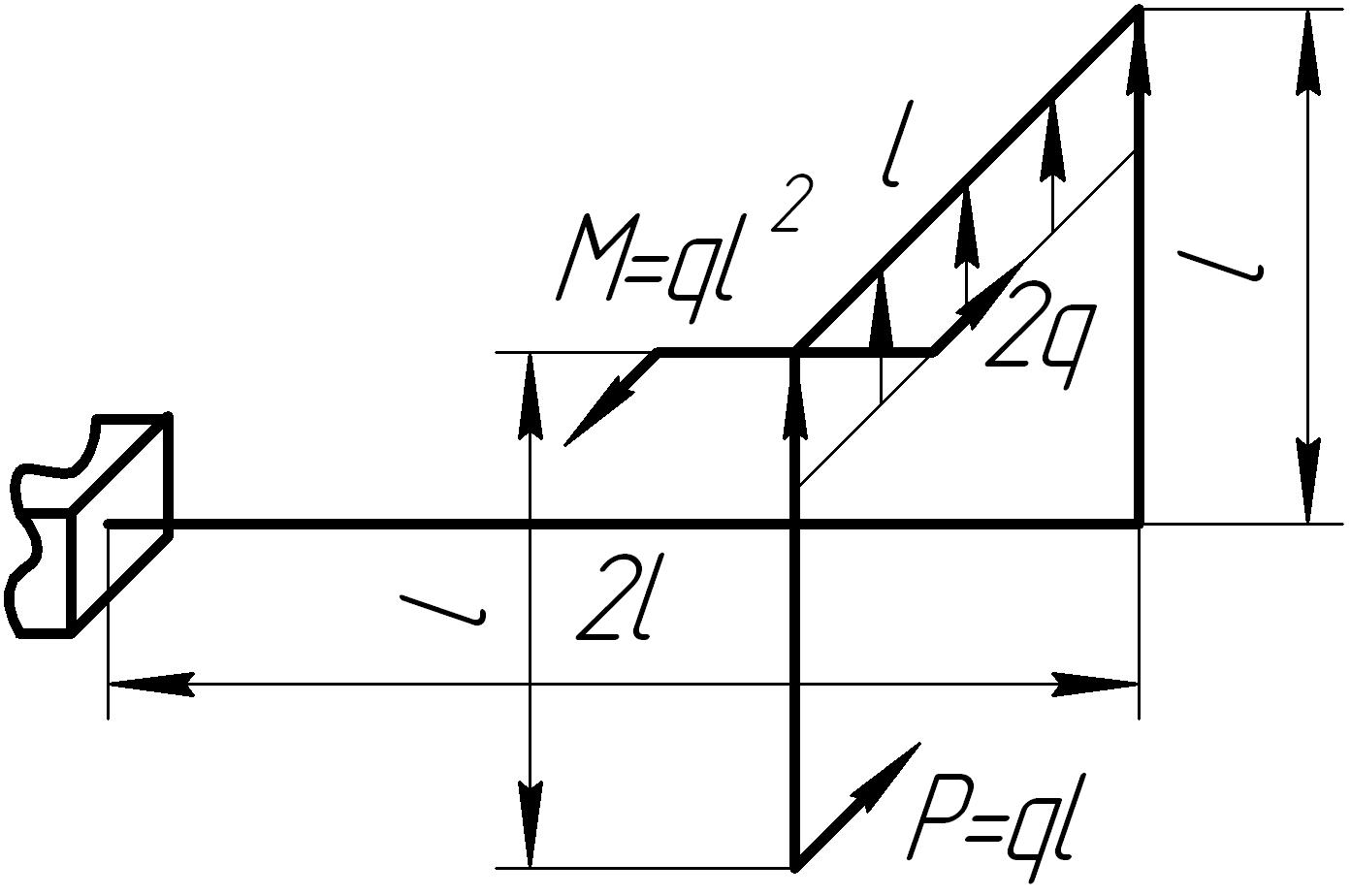
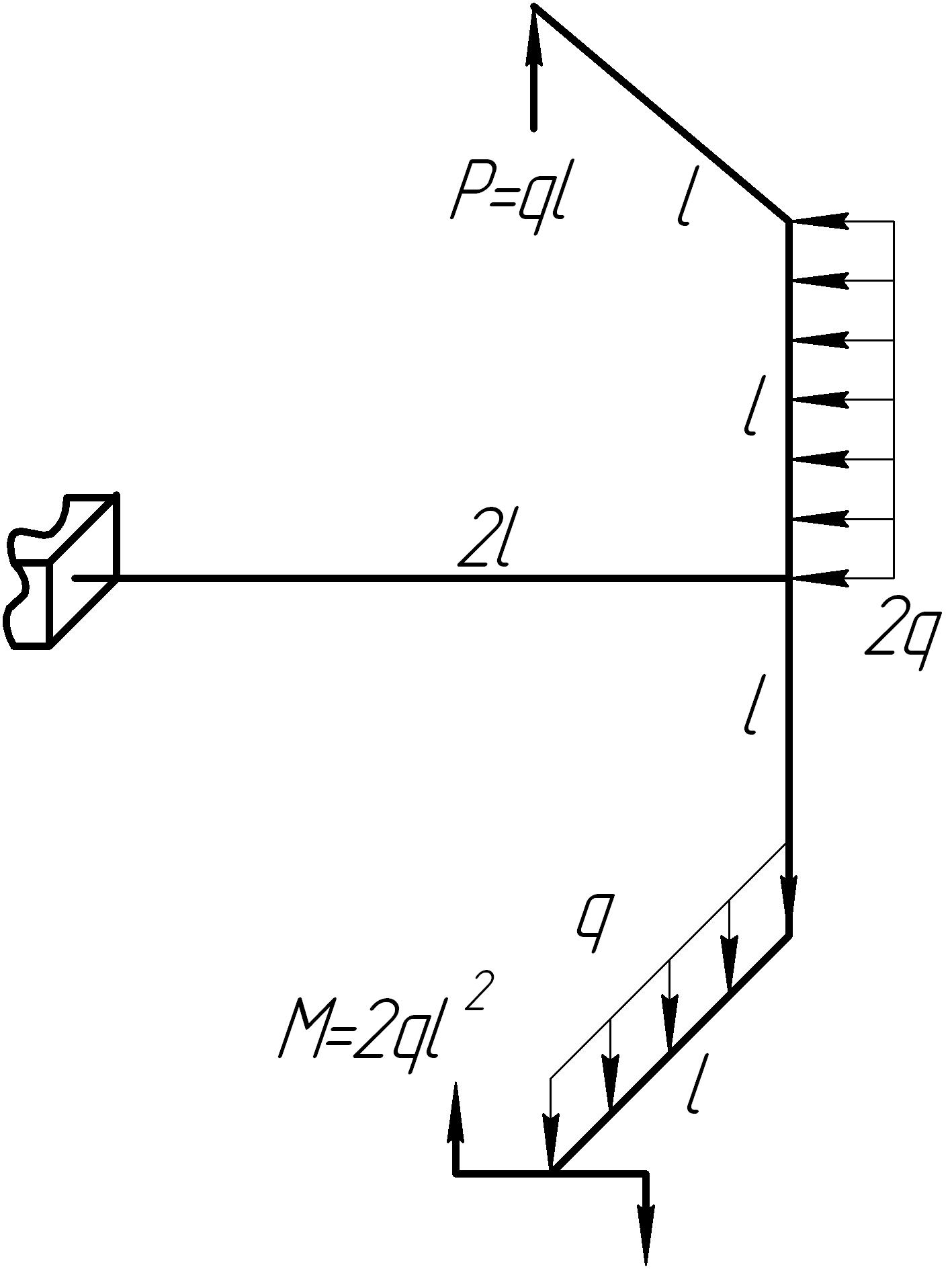
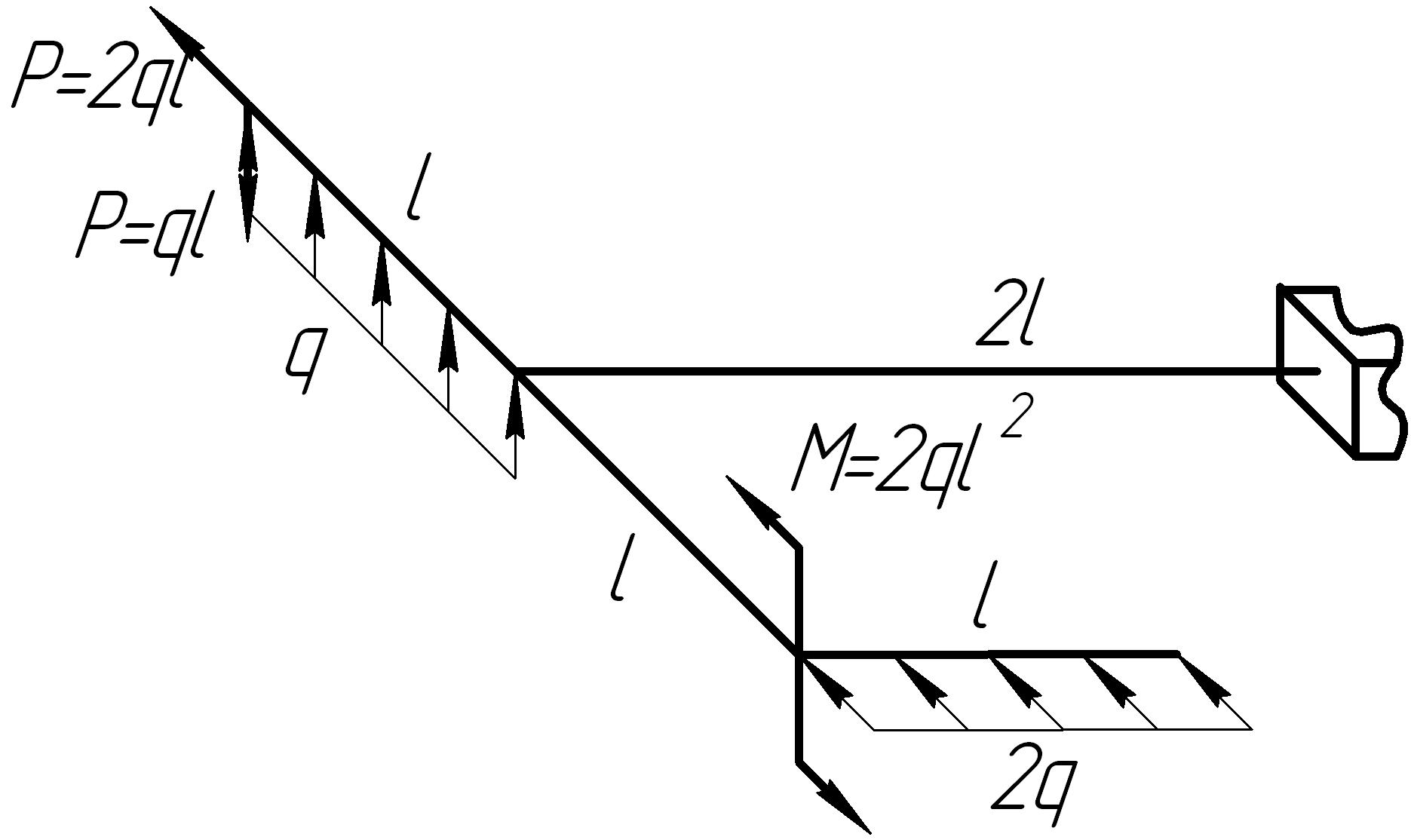
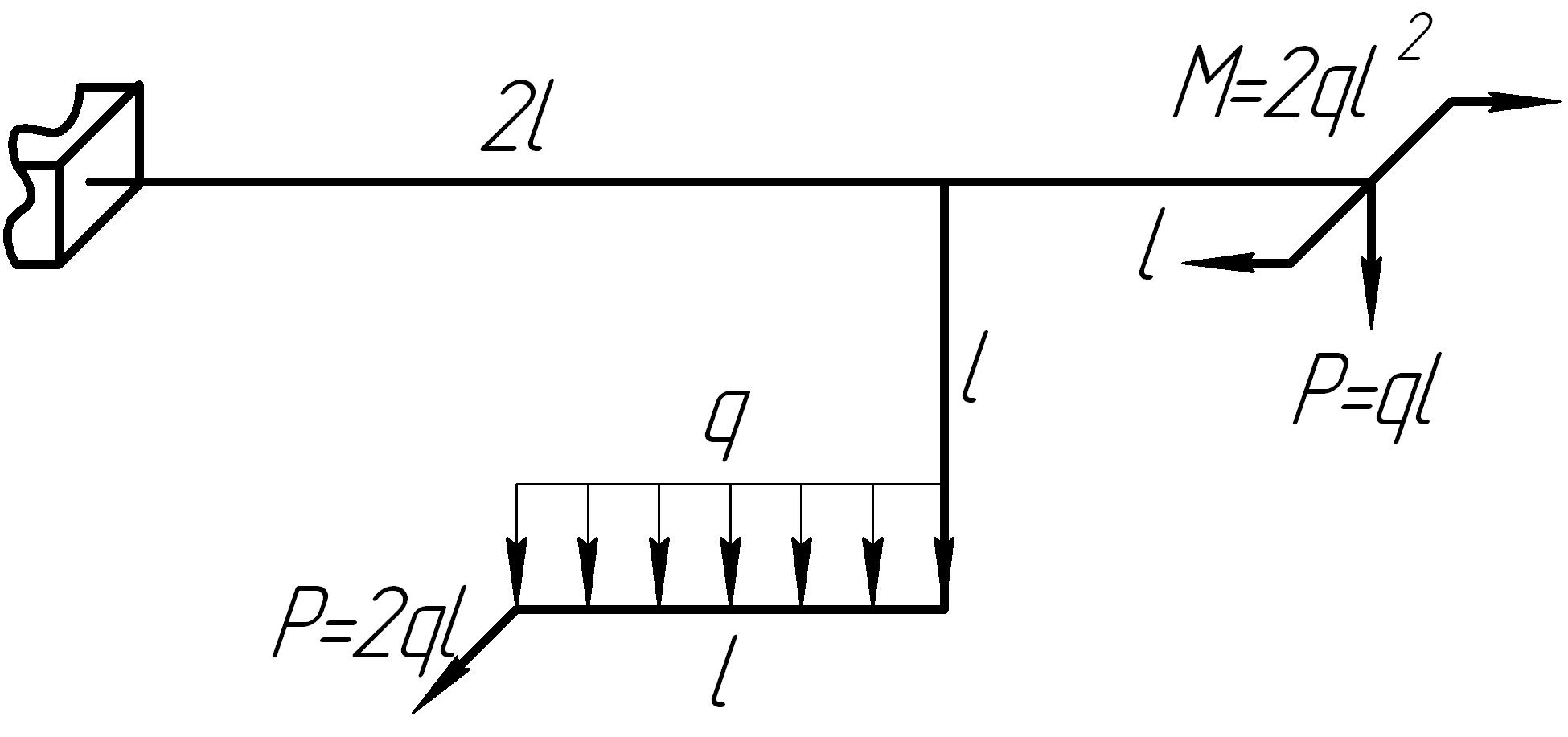
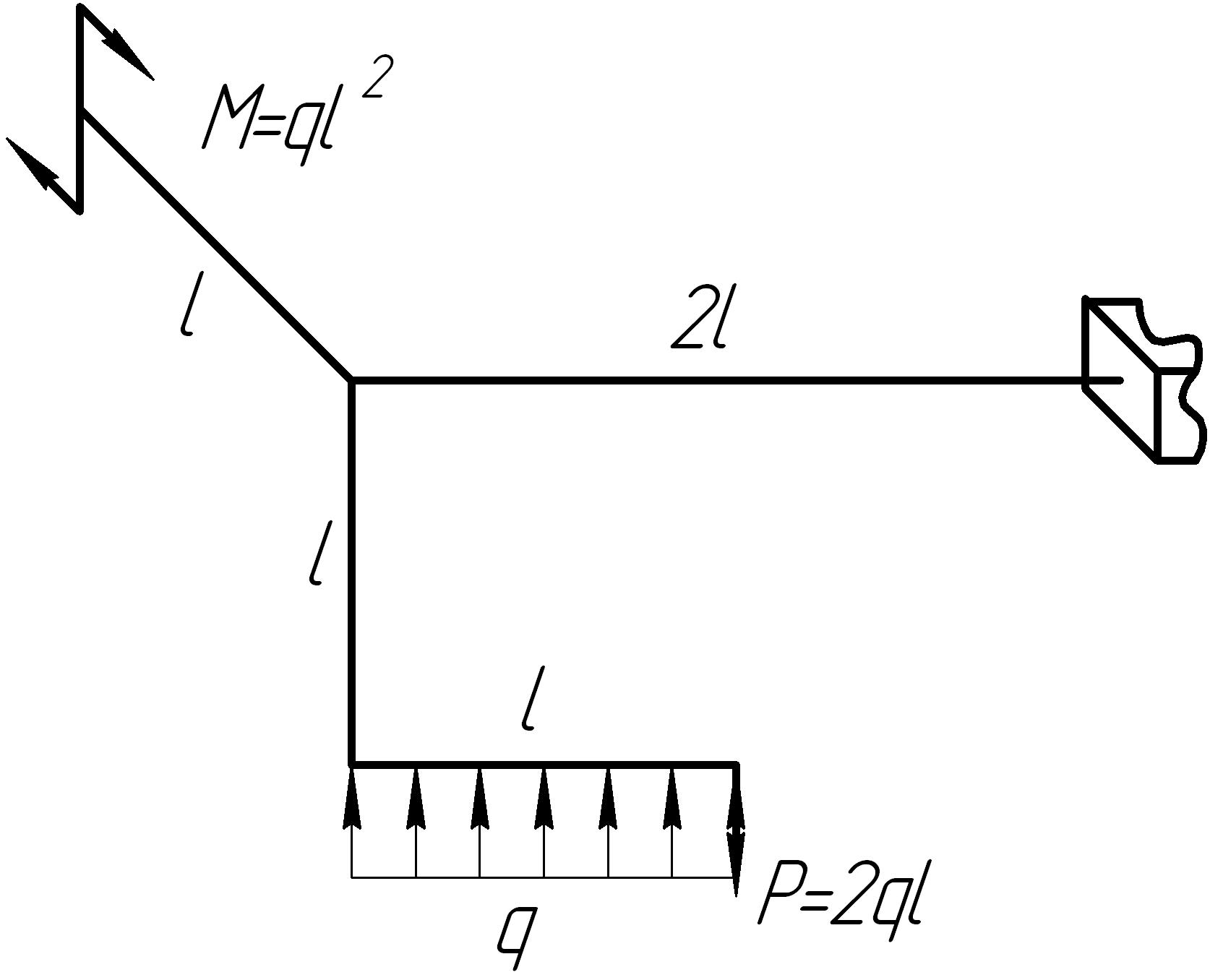
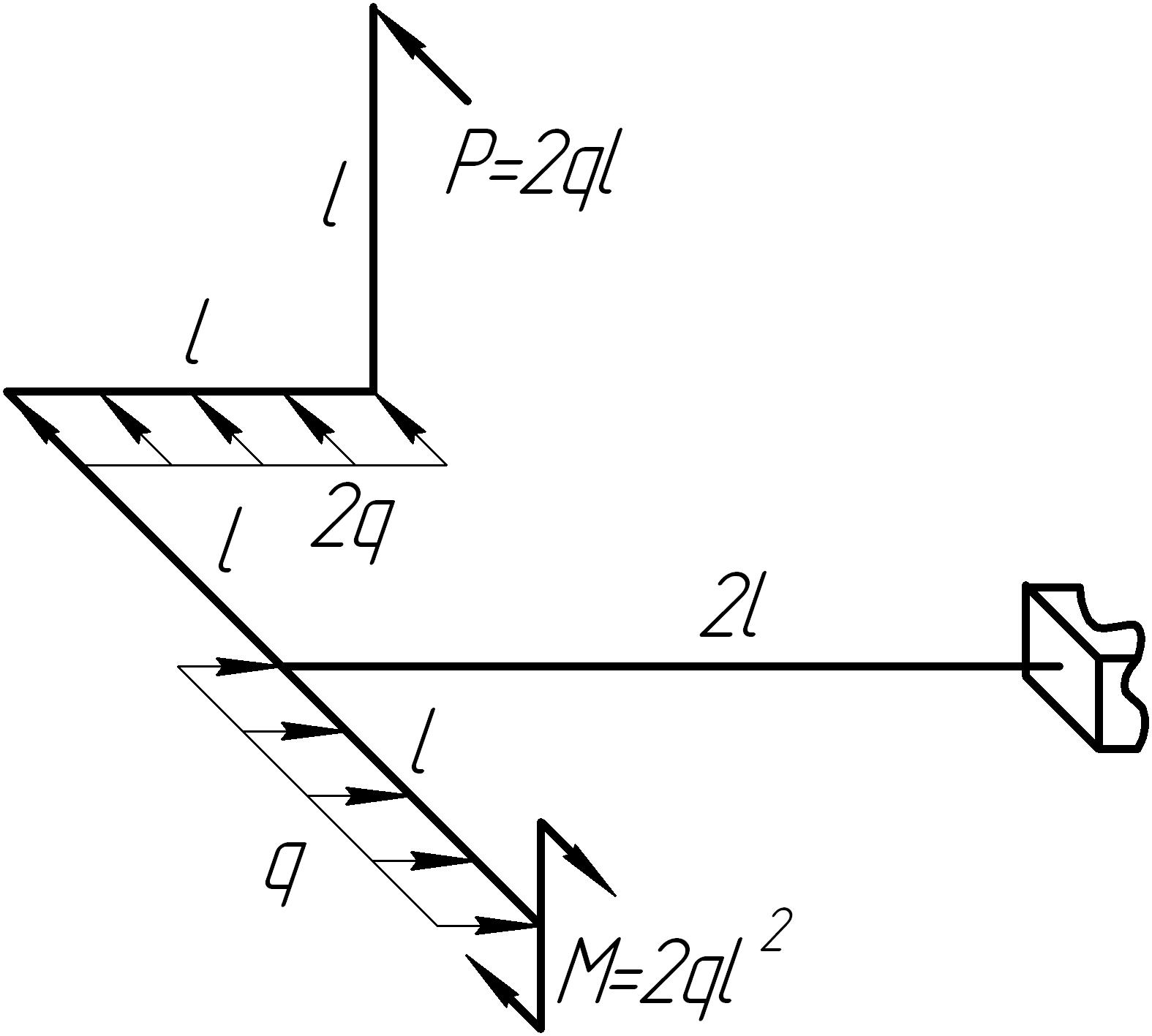
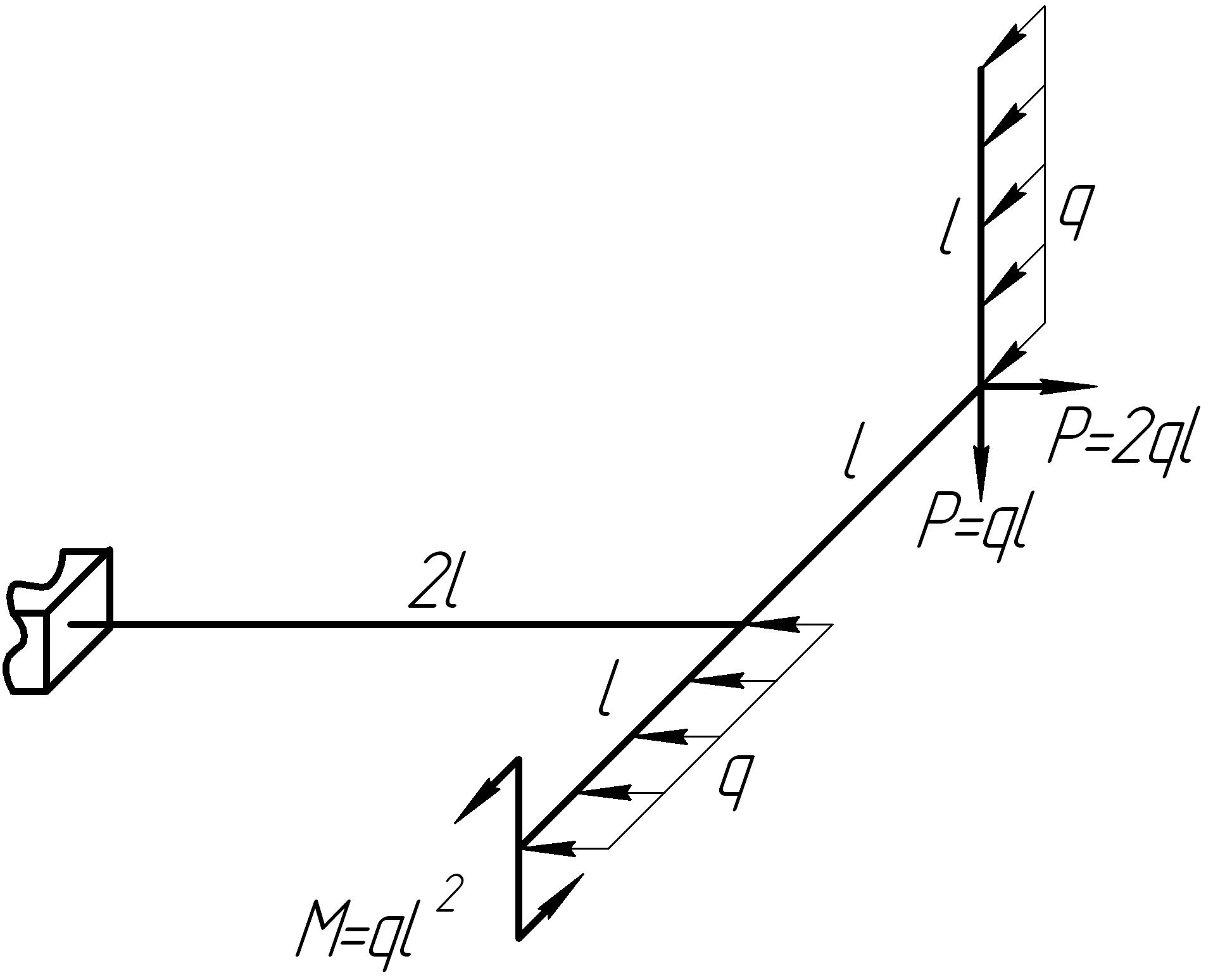
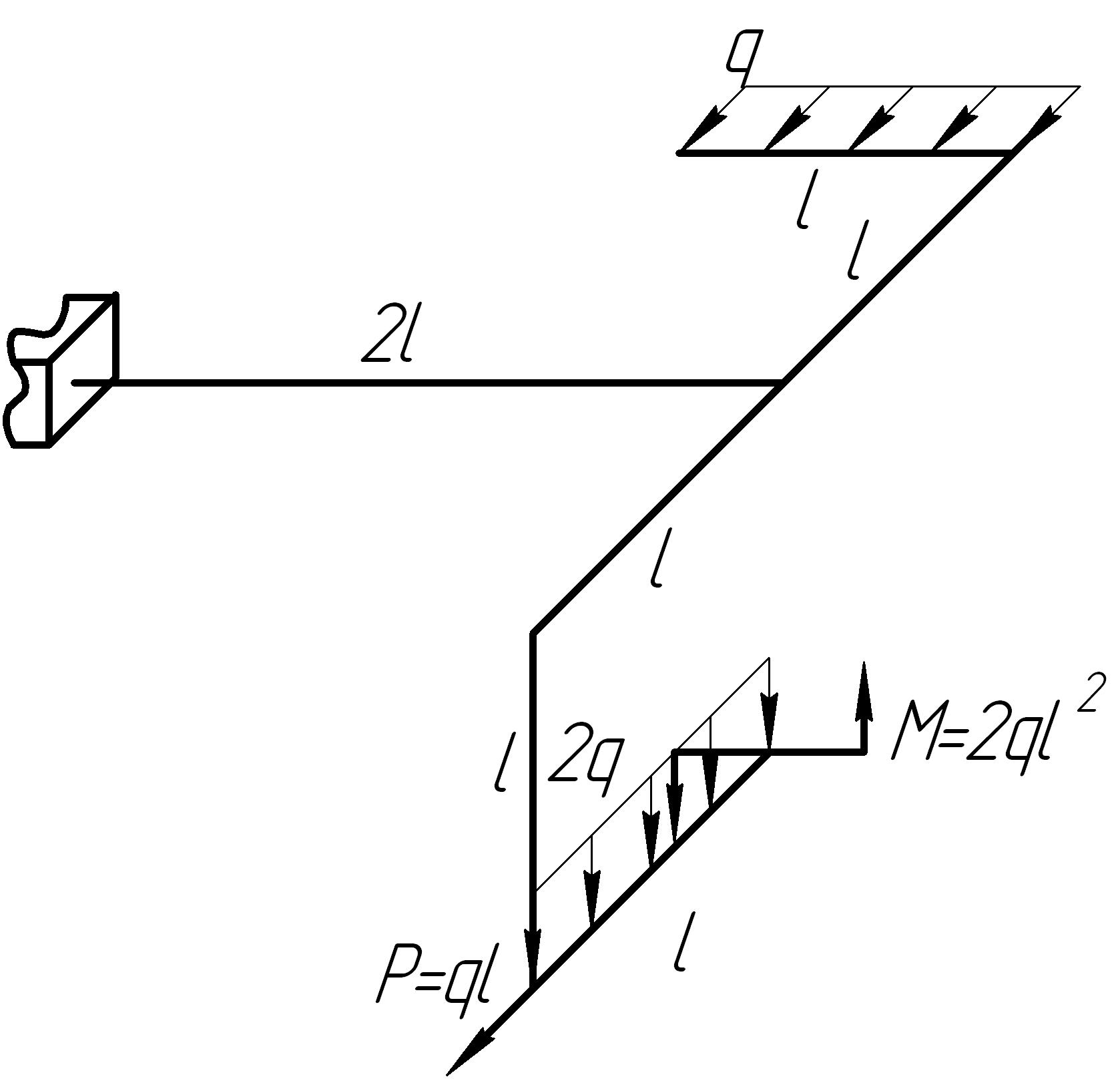
Задача 11
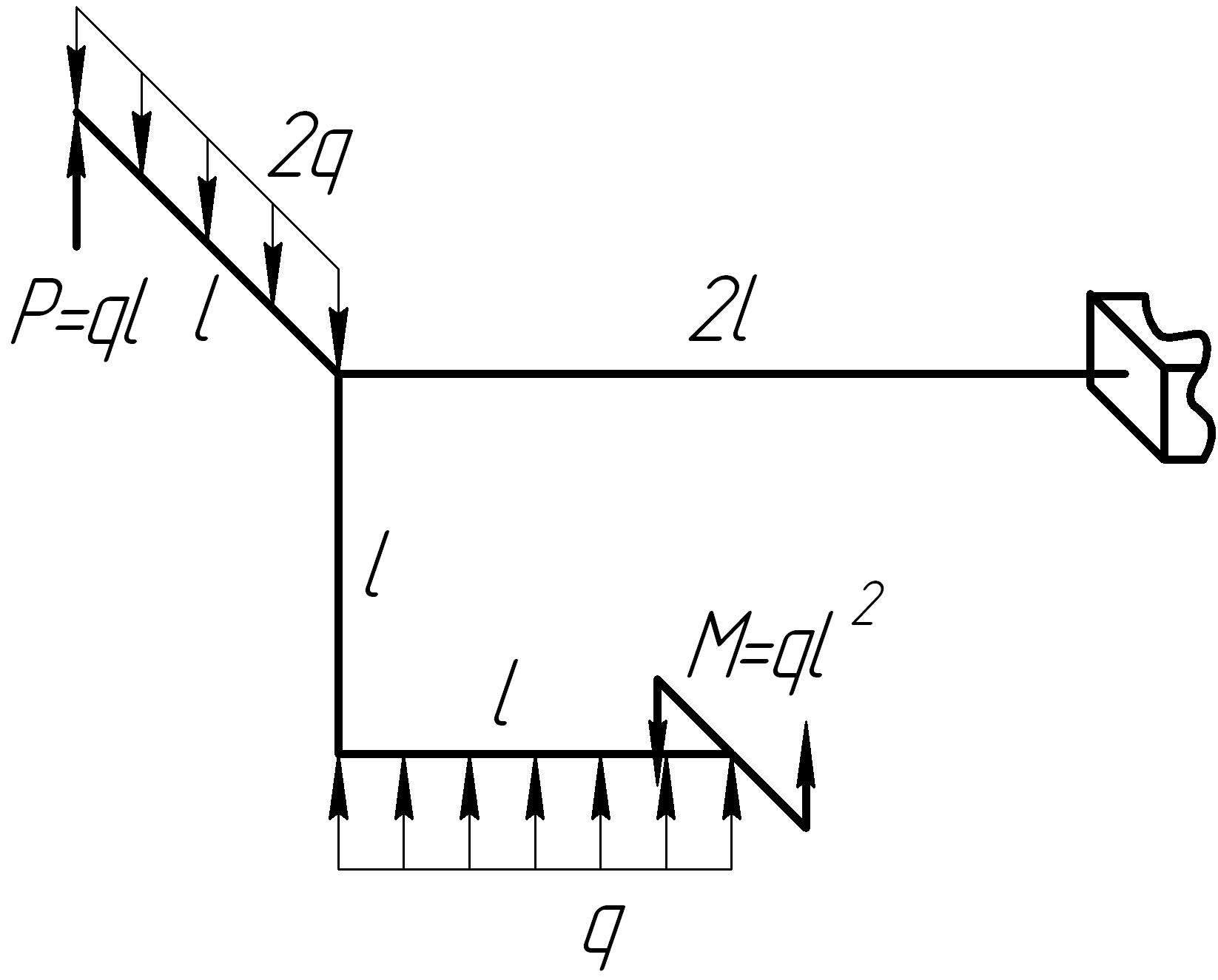
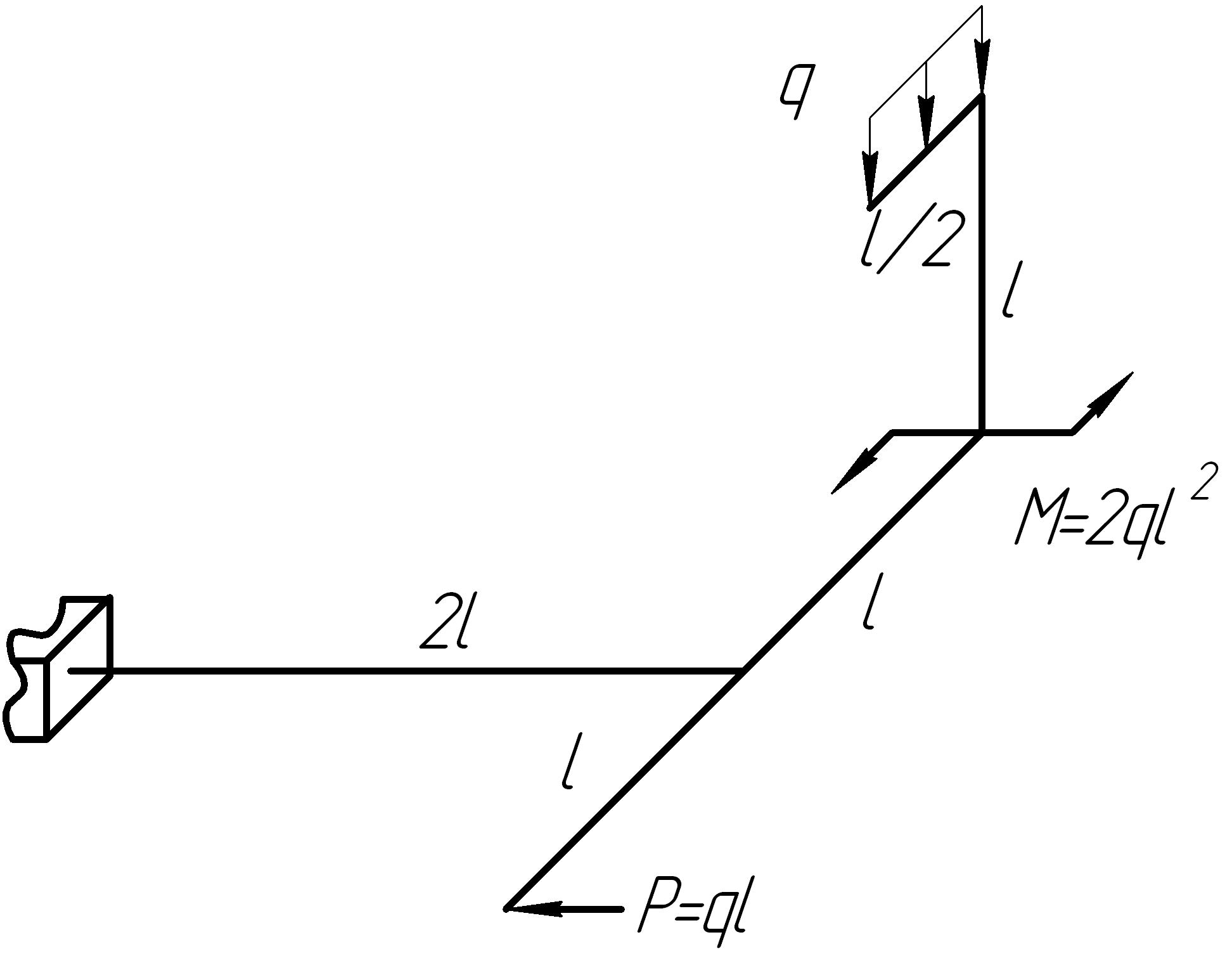
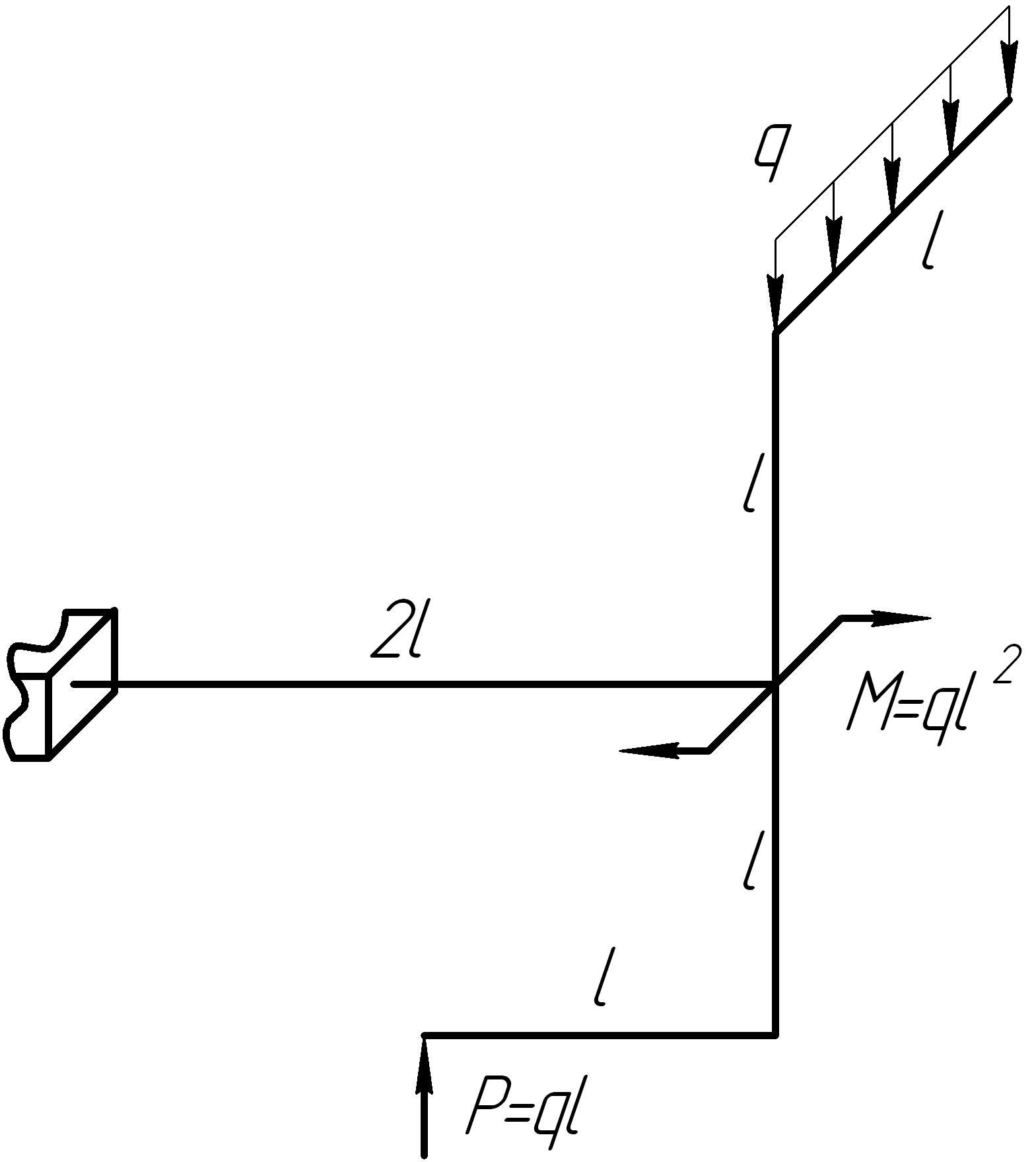
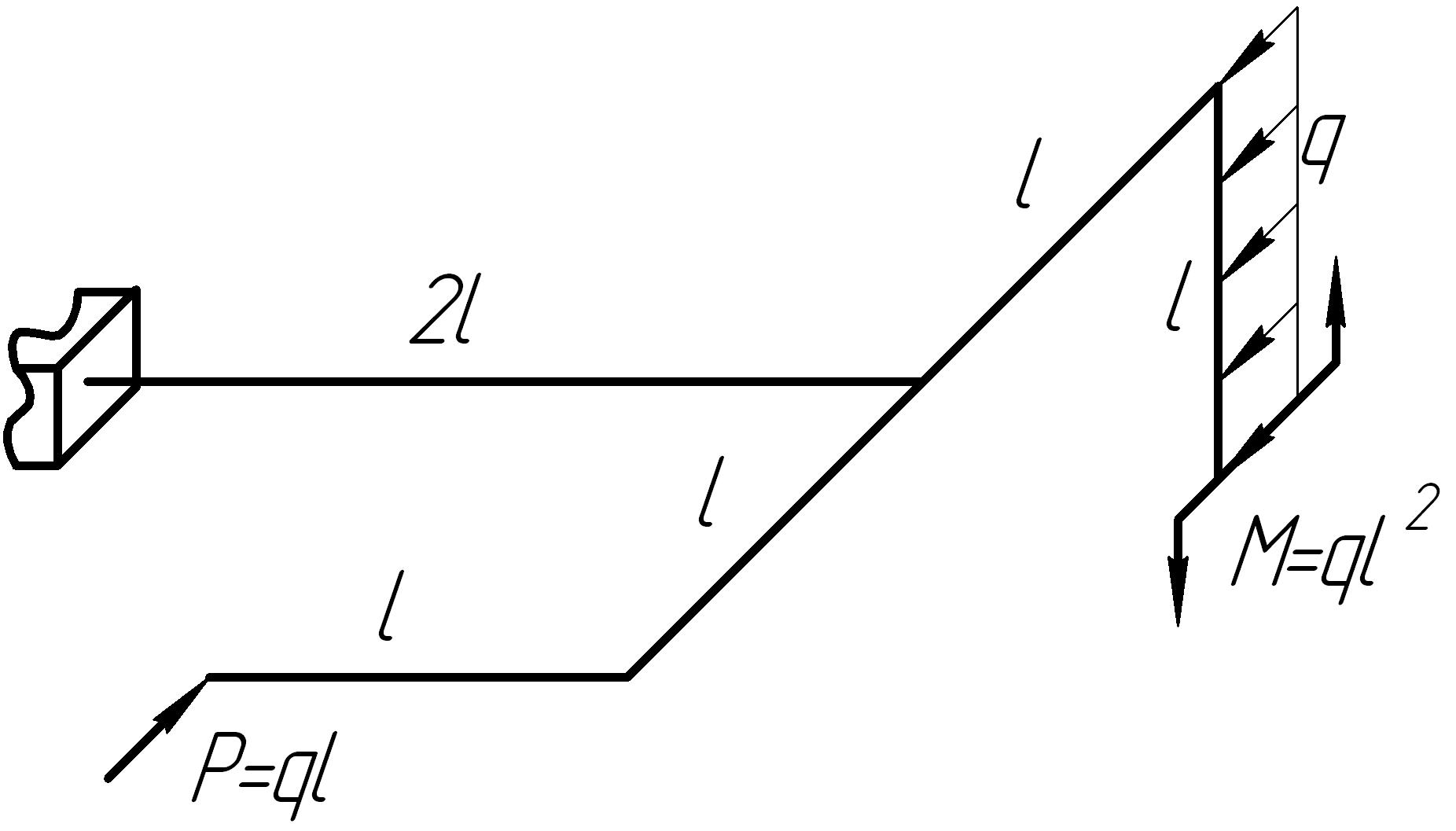
На основании исходных данных (рис. 6.11) построить эпюры внутренних силовых факторов в стержне с пространственно-ломаной осью.
1. |
|
2. |
|
3. |
|
4. |
|
Рис. 6.11
5. |
|
6. |
|
7. |
|
8. |
|
9. |
|
10. |
|
11. |
|
12. |
|
13. |
|
14. |
|
15. |
|
16. |
|
Рис. 6.11
17. |
|
18. |
|
19. |
|
20. |
|
21. |
|
22. |
|
23. |
|
24. |
|
25. |
|
26. |
|
Рис. 6.11
27. |
|
28. |
|
29. |
|
30. |
|
Рис. 6.11