5.5. Построение эпюр внутренних силовых факторов по составленных аналитическим выражениям

Построение эпюр внутренних силовых факторов рассмотрено отдельно только из методических соображений. В действительности же составление аналитических выражений функции внутренних силовых факторов и построение эпюр по участкам осуществляется одновременно.

Аналитические функции показывают характер изменения внутренних силовых факторов по участкам. При этом могут иметь следующие случаи:

а) внутренний силовой фактор аргумента не зависит – имеет постоянное значение. При этом для построения эпюры достаточно иметь значение в одной точке и провести отрезок в пределах участка на высоте внутреннего силового фактора параллельно базису.

б) внутренний силовой фактор в зависимости от аргумента меняется по прямопропорциональному, линейному закону. При этом для построения эпюры надо найти величины внутреннего силового фактора в начале и в конце участка. Отложив координаты найденных значений в определенном масштабе, соединяют полученные точки прямой линией.

в) внутренний силовой фактор в зависимости от аргумента меняется по сложной, криволинейной зависимости (в частности, квадратичная, кубическая параболы). Для построения эпюр внутренних силовых факторов в этих случаях требуются значения не только на границах, но и в середине участка. В этом случае эпюра строится по точкам.

Как было указано выше при построении эпюр внутренние силовые факторы, имеющие разные знаки, откладываются по разные стороны относительно базиса. При принятой схеме знаков внутренних силовых факторов эпюры изгибающих моментов всегда располагаются со сжатой стороны бруса. Поэтому говорят, что эпюры изгибающих моментов строятся на сжатых волокнах. Это правило в силе при построении эпюр изгибающих моментов для любых систем. В сложных стержневых системах – рамах расположение эпюр продольных и поперечных сил относительно базиса может быть произвольным, но при этом на эпюрах обязательно указываются знаки.

5.6. Проверка правильности построения эпюр

После построения эпюр необходимо убедиться в правильности их. Для этого применяются следующие правила.

1. На границах участков, где имеются сосредоточенные внешние силы, на эпюрах соответствующих внутренних силовых факторов должны быть скачки на величину приложенного внешнего сосредоточенного силового фактора. За величину скачка берется его абсолютная величина без учета знаков его составляющих. Так, например, на эпюрах продольных сил должны быть скачки в местах приложения растягивающих или сжимающих внешних продольных сил; на эпюрах крутящих моментов будут скачки в местах приложения сосредоточенных моментов величиной в приложенный момент и т.д.

2. На участках с распределенной нагрузкой (распределенная сила, распределенный момент) с известной интенсивностью силы и крутящий момент будут изменяться по линейной зависимости, а изгибающие моменты по криволинейной зависимости в зависимости от координаты.

3. Для проверки правильности построения эпюр применяются дифференциальные зависимости между внутренними и внешними силовыми факторами. Дифференциальные уравнения получаются из условий равновесия выделенного элемента.

Имеются следующие дифференциальные зависимости.

1. Между распределенными внешними и внутренними силами:

; ; .

2. Между распределенными внешними и внутренними моментами:

; ; .

3. Между внутренними моментами и поперечными силами при изгибе:

; .

Для проверки правильности построения необходимо иметь эпюры тех силовых факторов, которые связаны дифференциальной зависимостью.

Сущность проверки эпюр внутренних силовых факторов при помощи дифференциальных зависимостей заключается в использовании свойств функции и ее производной.

1. Производная равна нулю тогда, когда функция постоянная или, в частности, когда достигается минимального или максимального значения (рис. 5.6.1).

2. Если функция достигает экстремального значения, то уточнение максимум или минимум производится исследованием изменения знака производной в окрестности координаты экстремума при изменении аргумента. При этом, если при движении аргумента в сторону положительного направления знак производной меняется с (+) на (-), то достигается максимум; если наоборот, то минимум. Это хорошо видно из приведенного рисунка (рис. 5.6.1).

Рис. 5.6.1. Схема изменения знака производной для функции с максимумом (а), для функции с минимумом (б)

3. В тех точках, где производная имеет скачок, график функции при этом значении аргумента имеет излом.

4. В тех случаях, где функция имеет разрыв, производная имеет излом.

5. При изгибе в пределах участков с распределенной силой выпуклость кривой функции будет направлена навстречу стрелкам распределенной силы (рис. 5.6.2). Это вытекает из следующих дифференциальных зависимостей:

и .

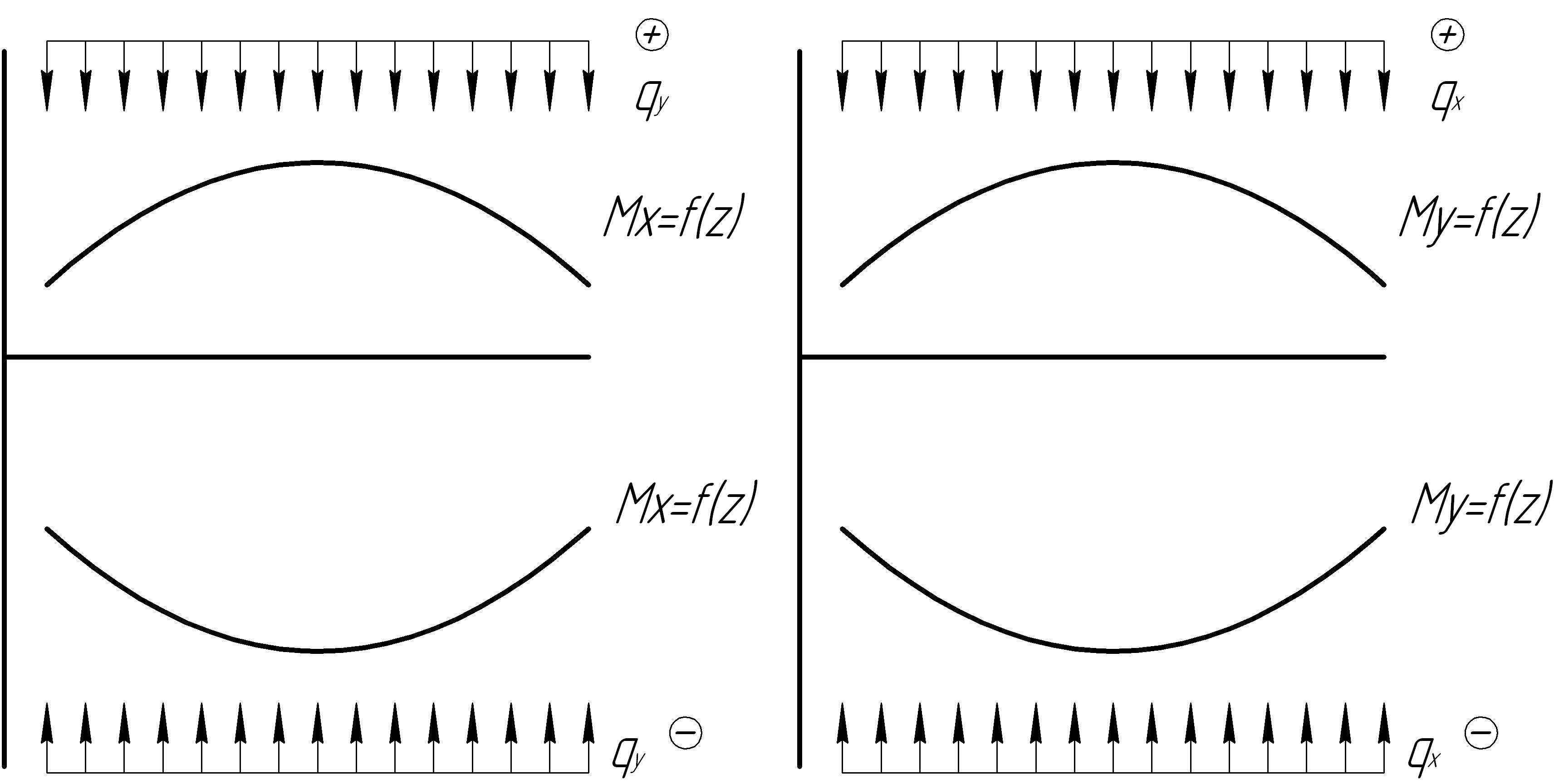
Рис. 5.6.2. Схема ориентировки выпуклости кривой в зависимости от знака распределенной силы