13.1. Методика решения задач

Задача 13.1.1. Проверить на выносливость тихоходный вал (рис. 13.4). Схема нагружений и расчет на статическую прочность приведены в задаче 4. Материал вала – сталь 45 нормализованная, Н/мм². Нормальные напряжения от изгиба изменяются по симметричному циклу, а касательные от кручения – по пульсационному (отнулевому).

Решение задачи:

1. Определим предел выносливости

Н/мм²

Н/мм²

Концентрация напряжений в сечениях I – I и II – II обусловлена наличием шпоночной канавки:

В сечении I – I

;

;

В сечении II – II

для углеродистых и легированных сталей.

Коэффициент, учитывающий качество поверхности ; .

Проверяем прочность в сечении I – I

Суммарный изгибающий момент:

Нмм

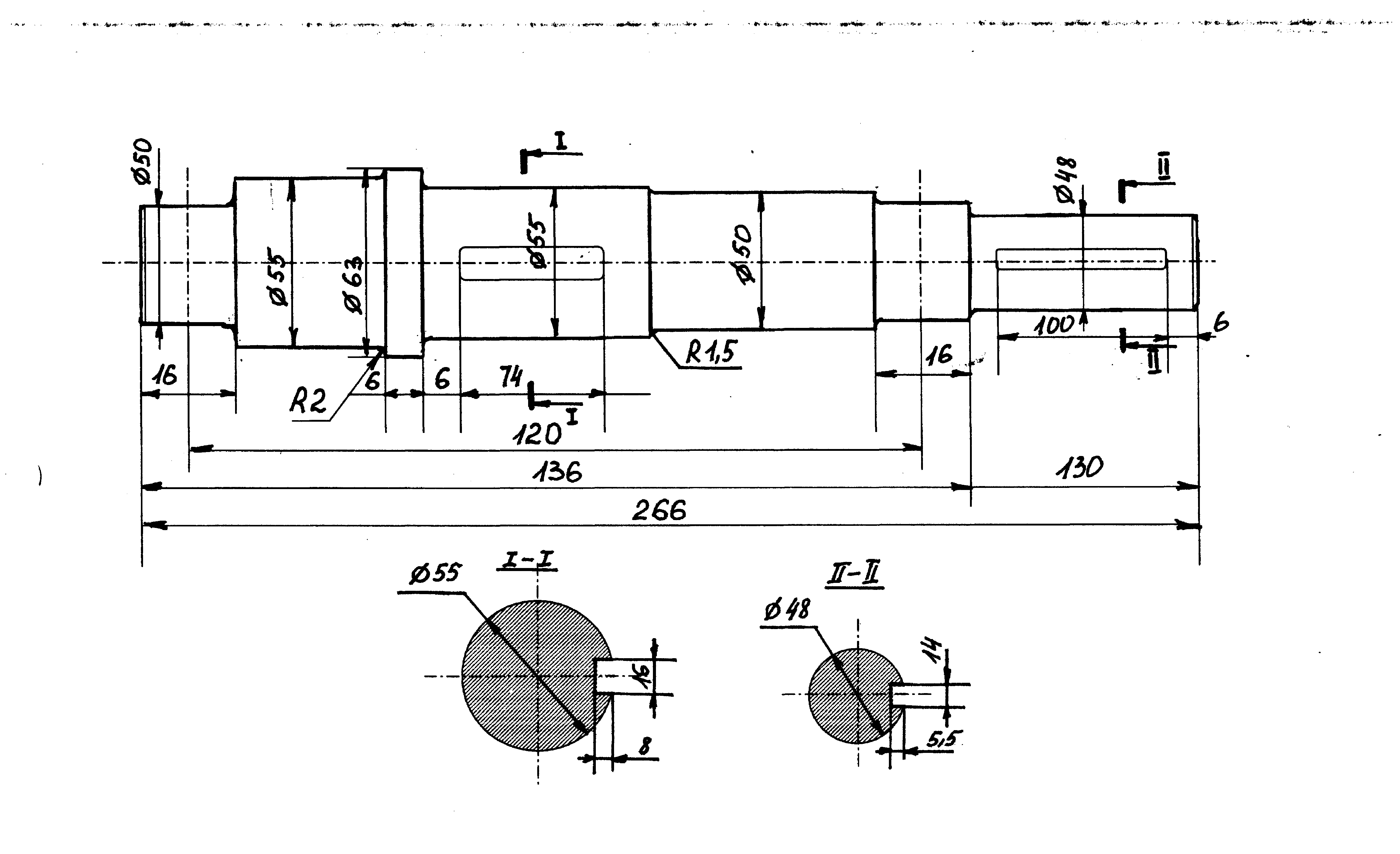
Рис. 13.4

Крутящий момент Нмм

Момент сопротивления сечения изгибу ( мм, мм, мм).

мм³

Момент сопротивления сечения кручению:

мм³

Максимальное номинальное напряжение изгиба:

Н/мм²

Номинальные касательные напряжения:

Н/мм²

Амплитуда номинальных напряжений изгиба:

Н/мм²

Среднее нормальное напряжение изгиба .

Амплитуда и среднее напряжение цикла касательных напряжений:

Н/мм².

Коэффициент снижения предела выносливости детали по нормальным напряжениям:

,

по касательным напряжениям

.

Коэффициент запаса прочности по нормальным напряжениям:

.

Коэффициент запаса прочности по касательным напряжениям:

.

Результирующий коэффициент запаса прочности сечения I – I

.

Сечения II – II

В этом сечении возникают только касательные напряжения кручения:

Н/мм²

Коэффициент снижения предела выносливости детали по касательным напряжениям:

.

Коэффициент запаса прочности:

.

Так как допускаемый коэффициент запаса усталостной прочности по пределу выносливости , следовательно, прочность вала обеспечена.

14. Продольный изгиб

Нагрузка, превышение которой вызывает потерю устойчивости первоначальной формы тела, называется критической.

Формула Эйлера для определения наименьшего значения критической силы

, (14.1)

где - наименьший момент инерции сечения стержня;

- длина стержня.

Величина критической силы зависит от условий закрепления концов стержня. Различные случаи закрепления стержня приводятся к основному случаю введением в формулу (14.1), приведенной длины стержня

,

где - коэффициент приведения длины. Значение коэффициента для различных случаев закрепления концов стержня приведены на рис. 14.1.

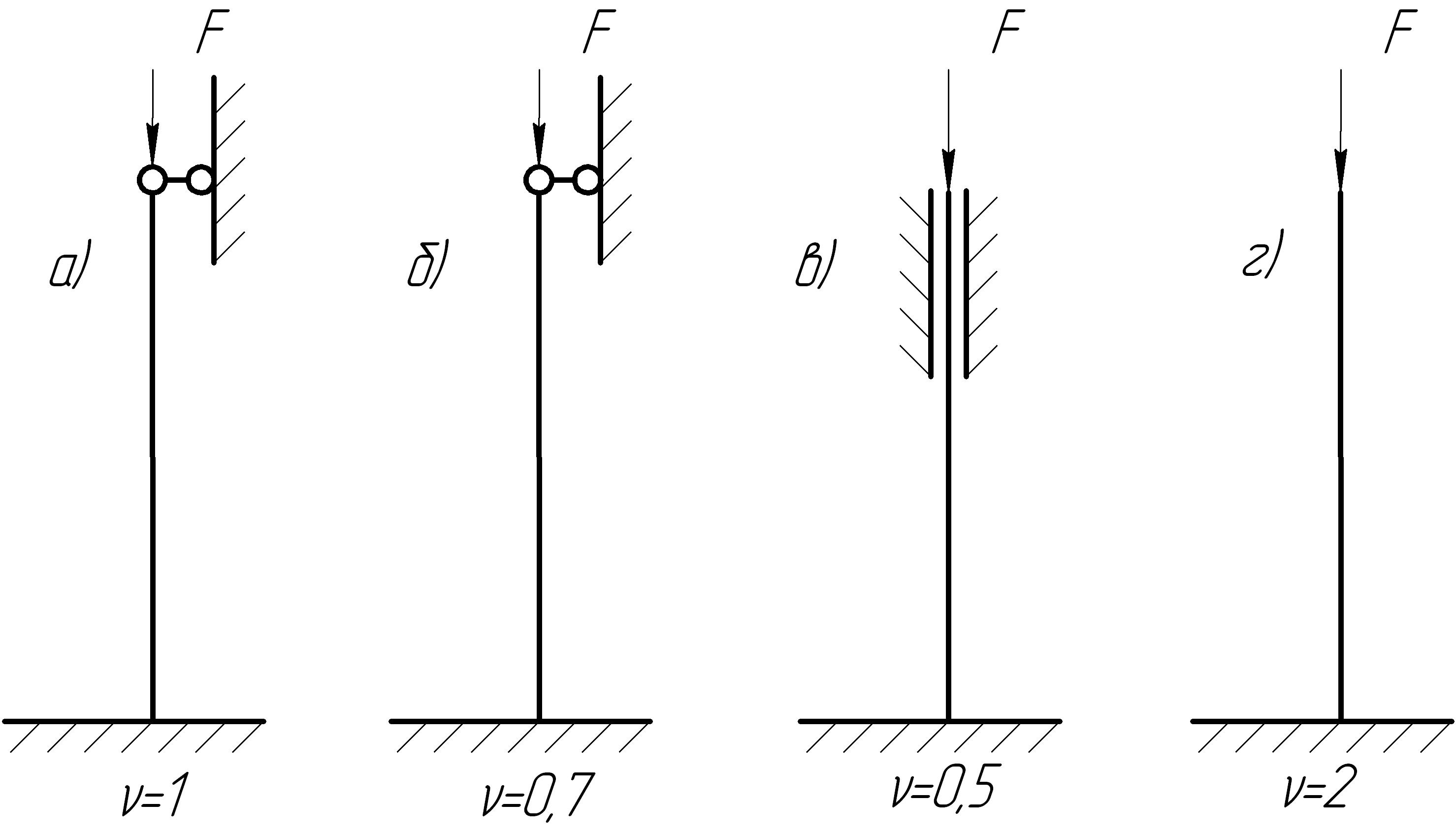
Рис. 14.1

Критическое напряжение

, (14.2)

где - гибкость стержня

- наименьший радиус инерции стержня.

, (14.3)

- площадь сечения стержня. Условие применимости формулы Эйлера.

, (14.4)

где - предел пропорциональности материала стержня.

Формула Ясинского для определения критических напряжений за пределом пропорциональности

, (14.5)

где и - коэффициенты, зависящие от материала, определяются по справочным таблицам.

Условие устойчивости

, (14.6)

где - продольная сила;

- полная площадь поперечного сечения стержня без учета местных ослаблений;

- коэффициент понижения основного допускаемого напряжения при расчете на устойчивость. Определяется по справочным таблицам;

- основные допускаемые напряжения (на сжатие).