Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Муромский институт (филиал)

Государственного образовательного учреждения

высшего профессионального образования

«Владимирский государственный университет»

Н.А. Лазуткина

О.Г. Кокорева

Механика

Учебное пособие для студентов специальности

280101.65 «Безопасность жизнедеятельности в техносфере».

Раздел «Сопротивление материалов»

Рекомендовано УМО РАЕ по классическому университетскому и техническому образованию в качестве учебного пособия для студентов высших учебных заведений

Муром

2009

УДК 535.3

ББК 64

Л 17

Рецензент:

Заведующая кафедрой «Техническая механика» Института горного дела, геологии и геотехнологий Сибирского Федерального Университета, кандидат технических наук, доцент

С.А. Косолапова

Печатается по решению редакционно-издательского совета

Муромского института (филиала)

Владимирского государственного университета

Л 17 Лазуткина, Н.А. Механика: учеб. пособие для студентов специальности 280101.65 «Безопасность жизнедеятельности в техносфере». Раздел «Сопротивление материалов» / Н.А. Лазуткина, О.Г. Кокорева. – Муром: Изд.-полиграфический центр МИ ВлГУ, 2009. – 150 с.: 56 ил. + 10 табл. – Библиогр.: 6 назв.

ISBN 978-5-8439-0222-3

УДК 535.5

ББК 64

В учебном пособии с достаточной полнотой изложены все вопросы, включаемые в курс сопротивления материалов. Методическая разработка предназначено для расчетно-теоретической подготовки студентов, успешного освоения ими последующих профилирующих дисциплин и решения инженерных задач в будущей практической деятельности. В связи с этим в разработке большое внимание уделяется задачам анализа конструкций.

Учебная разработка предназначена в качестве пособия для студентов технических специальностей.

ISBN 978-5-8439-0222-3

ã Лазуткина Н.А., Кокорева О.Г., 2009

Муромский институт (филиал)

Государственного образовательного учреждения высшего профессионального образования

«Владимирский государственный университет», 2009

Содержание

Введение 7

1.ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ 9

1.1. Метод сечения и внутренние силовые факторы 9

2. РАСТЯЖЕНИЕ И СЖАТИЕ 13

2.1. Расчеты на прочность 15

3. СДВИГ И КРУЧЕНИЕ 17

3.1. Расчеты на прочность и жесткость 19

4. ИЗГИБ БРУСЬЕВ 21

4.1. Расчеты на прочность и жесткость 24

5. Порядок решения задач 31

5.1. Составление расчетной схемы 31

5.2. Статически определимая система и нахождение реакций опор 32

5.3. Определение количества участков 33

5.4. Составление аналитического выражения внутренних силовых 34

факторов 34

5.5. Построение эпюр внутренних силовых факторов по составленных аналитическим выражениям 36

5.6. Проверка правильности построения эпюр 38

5.7. Определение опасного сечения 40

6. ЗАДАЧИ для выполнения практических работ 41

7. Примеры решения задач 73

8. НАПРЯЖЕННОЕ И ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ ПРИ СЛОЖНОМ НАГРУЖЕНИИ. ГИПОТЕЗЫ ПРЕДЕЛЬНЫХ СОСТОЯНИЙ 113

9. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИЙ, ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ 115

10. УСТОЙЧИВОСТЬ ДЕФОРМИРОВАННОГО СОСТОЯНИЯ 115

КОНСТРУКЦИЙ 115

11. МЕСТНЫЕ И КОНТАКТНЫЕ НАПРЯЖЕНИЯ. ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ 116

12. СЛОЖНОЕ СОПРОТИВЛЕНИЕ 117

12.1. Понятие о сложном сопротивлении 117

12.2. Косой изгиб 117

12.3. Внецентренное растяжение (сжатие) 118

119

Рис. 12.2 119

Максимальное напряжение при внецентренном растяжении (рис.12.2) 119

12.4. Изгиб с кручением 120

12.5. Методика решения задач 120

13. ОСНОВЫ РАСЧЕТА НА ВЫНОСЛИВОСТЬ 134

13.1. Методика решения задач 138

14. Продольный изгиб 142

14.1. Методика решения задач 143

14.2. Задачи для самостоятельного решения 148

Библиографический список 151

Муромский институт (филиал) 152

Введение

Учебное пособие написано по программе курса механики для студентов специальности 280101.65 «Безопасность жизнедеятельности в техносфере» и посвящено изучению важнейших разделов сопротивления материалов.

Методическая разработка предназначено для расчетно-теоретической подготовки студентов, успешного освоения ими последующих профилирующих дисциплин и решения инженерных задач в будущей практической деятельности. В связи с этим в разработке большое внимание уделяется задачам анализа конструкций.

Учебное пособие содержит как общетеоретические положения, так и конкретные инженерные решения, обобщающие результаты теоретического анализа и практического опыта машиностроения. Материалы справочного характера, содержащиеся в разделах, дают представление о техническом уровне и возможностях элементов конструкций и будут полезными при выполнении самостоятельных заданий.

Цель учебного пособия – научить студентов самостоятельной работе с типовыми заданиями курса механики.

В методической разработке большое внимание уделено вопросам организации самостоятельной работы студентов, поскольку роль СРС в формировании современного специалиста исключительно велика. Именно в процессе самостоятельной работы студента воспитываются важнейшие качества, необходимые для специалиста высшей квалификации. Самостоятельная работа студентов предполагает усвоение и углубление знаний по изучаемым дисциплинам, приобретение навыков самообразования. С первых же занятий по механике студент включается в систему подготовки, цель которой – научить его работать самостоятельно. На занятиях студенты получают установки, посвященные организации самостоятельной работы по механике. Они помогают студенту приобрести устойчивые навыки работы с книгой, конспектом. Правила ведения конспекта, умение следить за мыслью лектора и записывать главное, приобретение навыков четкого изображения схем и чертежей во многом определяют учебные успехи студентов, формируют стиль самостоятельной работы.

Структура учебного пособия содержит: теоретические положения курса сопротивления материалов по видам деформации: растяжение – сжатие, сдвиг, кручение, изгиб; задания для выполнения практических работ; порядок и примеры решения задач; напряженное и деформированное состояние при сложном нагружении; расчет статически неопределимых систем; расчет на прочность при переменных нагрузках; расчет на выносливость и продольный изгиб

Изложенный в методической разработке материал дает возможность студентам более целенаправленно проводить самостоятельную работу по глубокому изучению и закреплению основных тем курса и контролю усвоения изучаемого материала.

При подготовке учебного пособия использованы материалы к.т.н., доцента Андреева В.Д.

1.ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ

1.1. Метод сечения и внутренние силовые факторы

Конструкция считается прочной, если размеры каждого ее элемента подобраны так, что способны воспринимать заданную нагрузку, не разрушаясь. Жесткость конструкции обеспечивается, если под действием заданной нагрузки деформации не превышают допускаемые пределы.

Конструкция считается устойчивой, если она сохраняет перво­начальную форму упругого равновесия при действии внешних на­грузок.

Использование указанных методов расчета должно обеспечи­вать надежность работы конструкции и сочетаться с принципом экономичности ее изготовления и эксплуатации.

Рассматривают типичные элемен­ты конструкций: брус, пластинка, оболочка. Внешние нагрузки, действующие на элементы сооружений, подразделяют на сосредо­точенные и распределенные, статические и динамические. Все ре­альные силы — это силы, распределенные по некоторой площади или объему. Однако, распределенную нагрузку на небольшой площади, размеры которой очень малы по сравнению с размерами всего эле­мента, можно заменить сосредоточенной равнодействующей силой, что упростит расчет. Распределенные нагрузки имеют единицы си­лы, отнесенной к единице длины, или к единице поверхности или объема.

Статически нагружают конструкции постепенно, и, будучи при­ложены к сооружению, они не меняются или меняются во времени незначительно. При воздействии статических нагрузок на конструк­цию все ее части находятся в равновесии; ускорения элементов конструкции отсутствуют или настолько малы, что ими можно пре­небречь. Если же эти ускорения значительны, т. е. изменение ско­рости элементов машины, происходит за сравнительно небольшой: период времени то мы имеем дело с приложением динамических нагрузок.

Примерами таких нагрузок могут служить внезапно при­ложенные нагрузки, ударные и повторно-переменные. Действие таких нагрузок сопровождается возникновением колебаний конструкций или сооружений. Вследствие изменения скорости колеблющихся масс возникают силы инерции, пропорциональные (согласно второму законы Ньютона) колеблющимся массам и ускорениям.

Методы расчета элементов конструкций излагаются на основе следующих упрощений и допущений: материал тела имеет сплошное непрерывное строение, т. е. не принимается во внимание дискретная атомистическая структура вещества; материал тела однороден, т. е. обладает во всех точках одинаковыми свойствами; материал тела изотропен, т. е. обладает во всех направлениях одинаковыми свойствами; в теле до приложения нагрузки нет внутренних (начальных) усилий; результат воздействия на тело системы сил равен сумме результатов воздействия тех же сил, прилагаемых, к телу последовательно и в любом порядке.

Первую часть механики - сопротивление материалов - рекомендуется изучать по одному из приведенных ниже учебников с тщательным разбором решений типовых задач.

Метод сечений применяется следующим образом. Нагруженный произвольной системой брус, находящийся в равновесии, мысленно разрезается поперечным сечением на две части. Одна из частей мысленно отбрасывается, а вторая рассматривается в равновесии (рис. 1.1). Равновесие рассматриваемой части достигается приложением по месту сечения системы сил, эквивалентной действию отброшенной части. Приложенная система сил приводится в центр тяжести сечения (на ось бруса). Такое приведение в общем случае дает главный момент ( ) и главный вектор внутренних сил. При расчетах на прочность и жесткость удобно оперировать не главным моментом и главным вектором, а их проекциями относительно главных центральных осей поперечного сечения и оси бруса. - символическое выражение внешнего силового фактора (в конкретном случае это сосредоточенные и распределенные активные и реактивные моменты).

Рис. 1.1 - Схема применения метода сечения при определении внутренних силовых факторов

Проекции главного момента и главного вектора на оси выбранной системы координат, называются внутренними силовыми факторами. Они обозначаются и называются так: и (проекции главного вектора на оси и ) – поперечные (перерезывающие) силы; (проекция главного вектора на ось бруса) называется продольной (нормальной) силой; и (проекции главного вектора на оси и ) называются изгибающими моментами; (проекция главного момента на ось бруса называется крутящим моментом.

Поскольку приложением внутренних силовых факторов достигается равновесие рассматриваемой части, то величины их определяются из уравнений статики:

1. ; ;

2. ; ;

3. ; ; (1.1)

4. ; ;

5. ; ;

6. ; .

В зависимости от конкретного характера действующих внешних сил те или иные уравнения системы (1.1) могут отсутствовать. По отсутствию или наличию уравнений системы (1.1) определяется вид нагруженности.

Различают простое нагружение и сложное нагружение. Принято различать следующие виды простого нагружения: осевое растяжение, осевое сжатие, изгиб, сдвиг (срез) и кручение. Сумма двух или более простых нагружений представляет собой сложное нагружение.

Например, при наличии проекций внешних сил только на ось (3 уравнения системы 1.1) получается простое осевое нагружение, в зависимости от знака проекции результирующей, осевое растяжение или сжатие; при наличии только уравнения (6) системы (1.1) получается простое нагружение – кручение; при наличии совместно уравнений (1 и 5) или (2 и 4) получается нагружение бруса, называемое поперечным изгибом и т.д.

Большинство деталей и конструкций испытывает сложное нагружение.

Таким образом, мысленно проводив в интересующем нас месте бруса сечение и составив уравнения статики (1.1) относительно принятой системы координат довольно просто можно определить внутренние силовые факторы в данном сечении. Легко заметить, что величина внутренних силовых факторов зависит от координаты проведенного сечения. Поэтому для выяснения закона изменения внутреннего силового фактора по длине бруса необходимо составить его аналитическое выражение в виде функции от аргумента , где координата центра тяжести поперечного сечения на оси бруса.

Часто аналитическая зависимость внутреннего силового фактора от координаты представляется графически. Такой графический рисунок называется эпюрой.

Эпюра строится на оси бруса, называемой на эпюрах базисом или базисной линией. Для удобства базисная линия выносится параллельно самой себе и для каждого силового фактора строится своя эпюра. Если силовой фактор имеет знак (+), то его величина в определенном масштабе откладывается вверх относительно базиса, а если (-), то – вниз. Таким образом, ордината, соответствующая определенному значению , указывает на величину внутреннего силового фактора в этом сечении. Если эпюра построена в масштабе, то из нее легко можно определить величину внутреннего силового фактора в интересующем нас сечении бруса.

Эпюра перед аналитическим выражением имеет то преимущество, что она наглядно описывает характер изменения внутренних силовых факторов по длине бруса.

Эпюра внутренних силовых факторов позволяет легко определить опасное сечение конструкции. Поскольку расчет на прочность ведется по опасному сечению, то отсюда станет ясным, почему столь важно умение составлять аналитическое выражение и построить эпюру внутренних силовых факторов.

2. РАСТЯЖЕНИЕ И СЖАТИЕ

Различают упругое, упругопластичное и вязкопластичное твердые тела. Упругое тело после снятия внешней нагрузки восстанавливает свои первоначальные размеры и форму. В этом случае деформация тела называется упругой. Упругопластичное тело восстанавливает свои первоначальные размеры и форму не полностью, т. е. имеет место остаточная деформация. В инженерных сооружениях и механических машинах не допустимо появление остаточных деформаций. От действия внешних нагрузок в поперечных сечениях возникают внутренние силовые факторы, которые определяют, используя метод сечений. Твердое тело, находящееся под действием внешних нагрузок, мысленно рассекают на две части и рассматривают равновесие одной из частей. Действие отброшенной части на оставшуюся заменяют внутренними нагрузками, приложенными в рассматриваемом сечении. Составляя уравнения равновесия оставшейся части от действия внешних и внутренних силовых факторов, находят последние.

Важнейшими понятиями являются напряжения и деформации.

При нагружении тела растягивающими или сжимающими силами определяются напряжения, деформации удлинения. Внутренняя сила взаимодействия, отнесенная к единице площади, выделенной в окрестности какой-либо точки поперечного сечения тела, называется напряжением в этой точке. Таким образом величина нап­ряжений в каждой точке сечения является мерой внутренних сил, которые возникают в материале в результате воздействия внешних нагрузок. Напряжения в поперечных сечениях тела определяются из соотношения:

σ=F/А;

где F—действующее, в сечении усилие; А — лошадь поперечного сечения.

Напряжения и деформации в пределах упругой области связаны между собой с помощью закона Гука:

σ =εΕ,

где Е — модуль упругости материала.

Расчетные значения напряжений сравнивают с допускаемыми величинами, которые определяют путем деления некоторых предельных значений на коэффициент запаса прочности ([σ]=σ_пр/S). За предельные значения напряжений принимают предел прочности (для хрупких материалов) или предел текучести (для пластичных материалов), которые получают при испытаниях стандартных образцов на разрывных машинах. При этом строят в координатах напряжение - деформация условную диаграмму растяжения. Условной диаграмму называют потому, что напряжения и деформации вычисляют соответственно по отношению к первоначальной площади сечений и длинe образца. Используя условную диаграмму растяжения, необхо­димо уметь определять механические характеристики материала: предел пропорциональности, предел упругости, предел текучести и предел прочности и относительное остаточное удлинение при разрыве.

Для изучения значительных пластических деформаций необходимо знать истинную диаграмму растяжения, получаемую путем деления растягивающей силы на истинную площадь поперечно­го сечения образца (с учетом уменьшения поперечных размеров се­чения при растяжении).

Необходимо обратить внимание, что закон Гука, связывающий напряжения и деформации через модуль упругости материала, справедлив только до предела пропорциональности. Продольные деформации при растяжении связаны с поперечными деформациями с помощью коэффициента Пуассона.

При определении напряжений и деформаций в статически неопределимых системах необходимо учитывать, что возникающие при этом в стержнях силы зависят от жесткости стержня, т. е. от площадей поперечных сечений и модулей упругости материала.

В статически неопределимых системах необходимо также учитывать изменение температуры, так как это приводит к появлению внутренних усилий.

2.1. Расчеты на прочность

При проектировании элемента конструкции необходимо определить размеры, обеспечивающие его безопасную работу при заданных нагрузках. Для успешного решения этой задачи необходимо исходить из того, чтобы наибольшее расчетное напряжение в поперечном сечении элемента конструкции, возникшее при заданной нагрузке, было меньше того предельного напряжения, при котором возникает опасность появления пластической деформации или опасность разрушения.

Отношение предельного напряжения к расчетному называется коэффициентом запаса прочности :

. (2.1)

При расчете элемента конструкции коэффициент запаса прочности задается заранее и называется нормативным или требуемым и обозначается .

Прочность элемента конструкции обеспечивается, если действительный коэффициент запаса прочности не ниже требуемого, т.е.

. (2.2)

Неравенство (2.2) выражает условие прочности элемента конструкции.

Разделив предельное напряжение на нормативный коэффициент запаса, получим допускаемое напряжение :

. (2.3)

Тогда условие прочности можно выразить неравенством:

, (2.4)

т.е. прочность элемента конструкции обеспечивается, если наибольшее напряжение, возникающее в нем, не превышает допускаемого.

Для пластических материалов как при растяжении, так и при сжатии предельным напряжением является предел текучести :

. (2.5)

Причем в этом случае .

Для хрупких материалов допускаемое напряжение растяжения и допускаемое напряжение сжатия получают исходя из пределов прочности или :

и (2.6)

в этом случае , а иногда и выше.

Условие прочности (2.4) применительно к расчетам на прочность при растяжении (сжатии) записывается в виде:

. (2.7)

Исходя из этого условия производят три вида расчетов.

Проектировочный расчет. При этом расчете известны нагрузки, действующие на брус, заданы или выбраны материал, допускаемое напряжение или нормальный запас прочности . Размеры поперечного сечения бруса, обеспечивающие требуемую прочность, определяем следующим образом: полагая , из уравнения (2.7) получаем расчетную формулу:

. (2.8)

Определив из этой формулы требуемую площадь поперечного сечения, в зависимости от формы (круг, квадрат и др.) находим его размеры.

Определение допускаемой нагрузки. В этом случае известны размеры бруса и его материал, а требуется определить максимально допустимую нагрузку. Для этого, приняв , из условия (2.7) находим:

. (2.9)

Затем с помощью метода сечения по найденному допускаемому значению продольной силы определяем допускаемое значение нагрузки.

Проверочный расчет. При этом расчете нагрузка бруса, его материал и размеры известны и требуется проверить, выполняется ли условие (2.7). Для этого определяем наибольшее расчетное напряжение в поперечном сечении бруса и сравниваем с допускаемым. Наибольшее расчетное напряжение не должно быть больше допускаемого, расчетное напряжение считают неопасным, если оно превышает допускаемое не более чем на 5%. Поперечное сечение бруса, в котором возникает наибольшее расчетное напряжение при растяжении (сжатии), называется опасным.

3. СДВИГ И КРУЧЕНИЕ

Сдвигом называют такой вид напряженного состояния, когда на гранях элемента действуют только касательные напряжения. При этом на двух взаимно перпендикулярных площадках действу­ют равные по величине и обратные по знаку касательные напряже­ния. Этот закон называется законом парности или взаимности ка­сательных напряжений и имеет силу, как для одноосного, так и для объемного напряженного состояний. Деформации, возникающие при сдвиге, называют угловыми деформациями или углом сдвига. Опы­ты показывают, что между напряжениями и деформациями при сдвиге существует линейная зависимость, аналогичная закону Гука при растяжении. Поэтому закон Гука при сдвиге имеет вид τ = γG, где γ — угол сдвига, a G — модуль сдвига.

Следует обратить внимание на то, что модуль продольной упругости, или модуль упругости первого рода Е и модуль упругости при сдвиге, или модуль упругости второго рода G для одного и того же материала связан через коэффициент Пуассона μ зави­симостью G=E/[2(l + μ)]. При расчетах на срез обычно принимают, что касательные напряжения распределены равномерно в попереч­ном сечении стержня и условие прочности на срез имеет вид: τ = F/A ≤ [τ].

Допускаемые напряжения [τ] на сдвиг (срез) составляют некоторую часть от допускаемых напряжений на растяжение. Рассчитывают на срез соединения заклепочные, болтовые, сварные, шпоночные и некоторые другие типы соединений.

При проведении прочностных расчетов на сдвиг (срез) необходимо научиться правильно определять площади среза для односрезных и многосрезных заклепок, а также для углового сварного шва, в котором срез происходит по биссекторной плоскости прямого угла поперечного сечения шва.

Если в поперечном сечении стержня действует крутящий момент Т, то стержень испытывает кручение. Необходимо, используя метод сечений, научиться строить эпюры крутящих моментов по длине стержня и определять возникающие касательные напряжения, определяемые из соотношения τ = Т/W_p, где W_p — полярный момент сопротивления сечения кручению.

В поперечном сечении стержня касательные напряжения распре­делены неравномерно. Так, для стержня с круглым поперечным се­чением касательные напряжения изменяются по линейному закону - от нуля на оси до максимального значения у поверхности. Так как сечения, расположенные у оси стержня, нагружены незначительно, то с целью экономии материала при кручении целесообразно ис­пользовать пустотелые профили. Крутящий момент в сечении скручиваемого стержня (вала) численно равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения.

3.1. Расчеты на прочность и жесткость

Условие прочности при кручении имеет вид:

. (3.1)

Предел текучести при кручении связан с пределом текучести при растяжении зависимостью , для пластичных материалов принимают [ ].

По условию прочности при кручении (3.1) выполняют три вида расчетов.

Проектировочный расчет. Определив крутящий момент в сечении бруса и приняв , находим требуемое значение полярного момента сопротивления:

. (3.2)

Затем, исходя из формулы поперечного сечения, находим диаметр бруса. Полученное значение диаметра в миллиметрах следует округлить до ближайшего большего четного числа или числа, оканчивающегося на 5.

Расчет допускаемой нагрузки. Определив полярный момент сопротивления сечения бруса и приняв , находим допускаемое значение крутящего момента:

. (3.3)

Затем, исходя из схемы нагружения, находим максимально допускаемую нагрузку.

Проверочный расчет. Определив максимальный крутящий момент в поперечном сечении бруса и полярный момент сопротивления сечения, находим и сравниваем его с .

Условие жесткости бруса при кручении состоит в том, чтобы относительный угол закручивания не превосходил некоторого заданного допускаемого значения , т.е.:

. (3.4)

В Международной системе единиц (СИ) допускаемый угол закручивания выражается в рад/м, но в практике часто допускаемый угол закручивания задается в град/м. Тогда это значение нужно перевести в единицы СИ, умножив на отношение , т.е.:

. (3.5)

Применяемые в машиностроении значения допускаемых углов закручивания колеблются в довольно широких пределах, чаще всего принимают

рад/м рад/мм или

град/м град/мм.

По условию жесткости (3.4) выполняют тоже три вида расчетов: проверочный – непосредственно по расчетной формуле (3.4); проектировочный – по расчетной формуле:

. (3.6)

Далее, в зависимости от формы сечения (круг или кольцо) по найденному значению , определяют диаметр или диаметры и .

Расчет допускаемой нагрузки выполняют по формуле:

. (3.7)

Объектом расчетов на прочность или жесткость часто становится брус, который называется валом. На вал при передаче мощности всегда действуют по крайней мере два скручивающихся момента (иногда три и больше). При расчете валов необходимо помнить известную из теоретической механики формулу, выражающую зависимость между вращающим (скручивающим) моментом , передаваемой мощностью и угловой скоростью :

, (3.8)

а также формулу, выражающую зависимость между угловой скоростью (с^-1) и частотой вращения (мин^-1):

. (3.9)

4. ИЗГИБ БРУСЬЕВ

При изгибе стержни подвергаются воздействию поперечной силы или изгибающего момента. Изгиб называется чистым, если действует только изгибающий момент, и поперечным, если действует нагрузка, перпендикулярная оси стержня. Брус (стержень), работающий на изгиб, обычно называют балкой. Балки являются наиболее часто встречающимися элементами сооружений и машин, вос­принимающими нагрузки от других элементов конструкций и пере­дающими их тем частям, которые поддерживают балку (чаще все­го опорам).

В строительных сооружениях и машиностроительных конструк­циях чаше всего можно встретить следующие случаи крепления ба­лок: консольные - с одним защемленным концом (с жесткой задел­кой), двухопорные - с одной шарнирно-неподвижной опорой и с од­ной шарнирно подвижной опорой и многоопорные балки. Если опорные реакции могут быть найдены из одних уравнений статики, то балки называют статически определимыми. Если же число неизвестных опорных реакций больше, чем число уравнений статики, то такие балки называют статически неопределимыми. Для опреде­ления реакций в таких балках приходится составлять дополнитель­ные уравнения - уравнения перемещений. При плоском поперечном изгибе все внешние нагрузки перпендикулярны к оси балки.

Определение внутренних силовых факторов, действующих в по­перечных сечениях балки, следует начинать с определения опорных реакций. После этого используем метод сечений, мысленно рассе­каем балку на две части и рассматриваем равновесие одной части. Взаимодействие частей балки заменяем внутренними факторами: изгибающим моментом и поперечной силой.

Поперечная сила в сечении равна алгебраической сумме проек­ций всех сил, а изгибающий момент равен алгебраической сумме моментов всех сил, расположенных по одну сторону от сечения. Знаки действующих сил и моментов следует определять в соответ­ствии с принятыми правилами. Необходимо научиться правильно определять равнодействующую силу и изгибающий момент от равномерно распределенной по длине балки нагрузки.

Следует иметь в виду, что при определении напряжений, возникающих при изгибе, принимают следующие допущения: сечения плоские до изгиба остаются плоскими и после изгиба (гипотеза плоских сечений); продольные соседние волокна не давят одно на другое; зависимость между напряжениями и деформациями линейная.

При изучении изгиба следует обратить внимание на неравно­мерность распределения нормальных напряжений в поперечном се­чении балки. Нормальные напряжения изменяются по высоте по­перечного сечения пропорционально расстоянию от нейтральной оси. Следует уметь определять напряжения изгиба, которые зависят от величины действующего изгибающего момента и момента сопро­тивления сечения при изгибе W.

Условие прочности при изгибе: σ = М/W ≤ [σ]. Значение W за­висит от размеров и формы поперечного сечения.

Наличие поперечной силы, действующей на балку, связано с возникновением касательных напряжений в поперечных сечениях, а по закону парности касательных напряжений — и в продольных сечениях. Касательные напряжения определяют по формуле Д. И. Журавского.

Поперечная сила сдвигает рассматриваемое сечение относитель­но смежного. Изгибающий момент, складывающийся из элементар­ных нормальных усилий, возникающих в поперечном сечении балки, поворачивает сечение относительно смежного, чем и обусловлено искривление оси балки, т. е. ее изгиб.

Когда балка испытывает чистый изгиб, то по всей длине балки или на отдельном ее участке в каждом сечении действует изги­бающий момент постоянной величины, а поперечная сила в любом сечении данного участка равна нулю. При этом в поперечных се­чениях балки возникают только нормальные напряжения.

Для того чтобы глубже разобраться в физических явлениях изгиба и в методике решения задач при расчете на прочность и жесткость, необходимо хорошо усвоить геометрические характеристики плоских сечений, а именно: статические моменты сечений, мо­менты инерции сечений простейшей формы и сложных сечений, определение центра тяжести фигур, главные моменты инерции сечений и главные оси инерции, центробежный момент инерции, изменение моментов инерции при повороте осей, теоремы о переносе осей.

При изучении этого раздела следует научиться правильно строить эпюры изгибающих моментов и поперечных сил, определять опасные сечения и действующие в них напряжения.

Помимо определения напряжений следует научиться определять перемещения (прогибы балки) при изгибе. Для этого используется дифференциальное уравнение изогнутой оси балки (упругой линии), записанное в общем виде.

Для определения прогибов проводится интегрирование уравнения упругой линии. При этом следует правильно определять постоянные интегрирования С и D исходя из условий опирания балки (граничных условий). Зная величины С и D, можно определить угол поворота и прогиб любого сечения балки. Изучение сложного сопротивления обычно начинают с косого изгиба.

Явление косого изгиба особенно опасно для сечений со значи­тельно отличающимися друг от друга главными моментами инерции; балки с таким сечением хорошо работают на изгиб в плоскости наибольшей жесткости, но даже при небольших углах наклона плоскости внешних сил к плоскости наибольшей жесткости в балках возникают значительные дополнительные напряжения и деформации.

Для балки круглого сечения, косой изгиб невозможен, так как все центральные оси такого сечения являются главными и нейтральный слой всегда будет перпендикулярен плоскости внешних сил. Ко­сой изгиб невозможен и для балки квадратного сечения.

При определении, напряжений в случае внецентренного растя­жения или сжатия необходимо знать положение главных центральных осей сечения именно от этих осей отсчитывают расстояния точки приложения силы и точки, в которой определяют напряжения.

Приложенная эксцентрично сжимающая сила может вызвать в поперечном сечении стержня растягивающие напряжения. В связи с этим внецентренное сжатее является особенно опасным для стерж­ней из хрупких материалов (кирпича, бетона), которые слабо со­противляются растягивающим усилиям.

В заключение следует изучить случай сложного сопротивления, когда тело испытывает одновременно несколько деформаций: на пример, изгиб совместно с кручением, растяжение-сжатие совмест­но с изгибом и т. д. При этом следует иметь в виду, что изгибающие моменты, действующие в различных плоскостях, могут складывать­ся как векторы.

4.1. Расчеты на прочность и жесткость

Балки рассчитывают на прочность по наибольшим нормальным напряжениям, возникающим в их поперечных сечениях. При поперечном изгибе балок наряду с нормальными возникают и касательные напряжения, обусловленные наличием поперечной силы, но они в подавляющем большинстве случаев невелики и при расчетах на прочность не учитываются.

Прочность балки обеспечена, если наибольшие по абсолютному значению нормальные напряжения, возникающие в опасном сечении, не превышают допустимых. Для балки, поперечные размеры которой по всей длине постоянны, опасное сечение то, в котором возникает наибольший по модулю изгибающий момент. Наибольшие нормальные напряжения возникают в точках опасного поперечного сечения, максимально удаленных от нейтральной оси. Эти точки принято называть опасными. Значения максимальных напряжений в опасных точках найдем по формуле (4.1):

; , (4.1)

где и - расстояние от нейтральной оси до наиболее удаленных точек соответственно в растянутой и сжатой зонах сечения.

Если материал балки хрупкий, например закаленная сталь, чугун, текстолит и др., то расчет на прочность при изгибе проводят по напряжениям растяжения и сжатия. У хрупких материалов предел прочности при сжатии выше предела прочности при растяжении ( ). Следовательно, поперечным сечением балок из хрупких материалов целесообразно придавать ассиметричную форму относительно нейстральной оси (рис. 4.1) и располагать балку так, чтобы большая часть материала находилась в растянутой зоне.

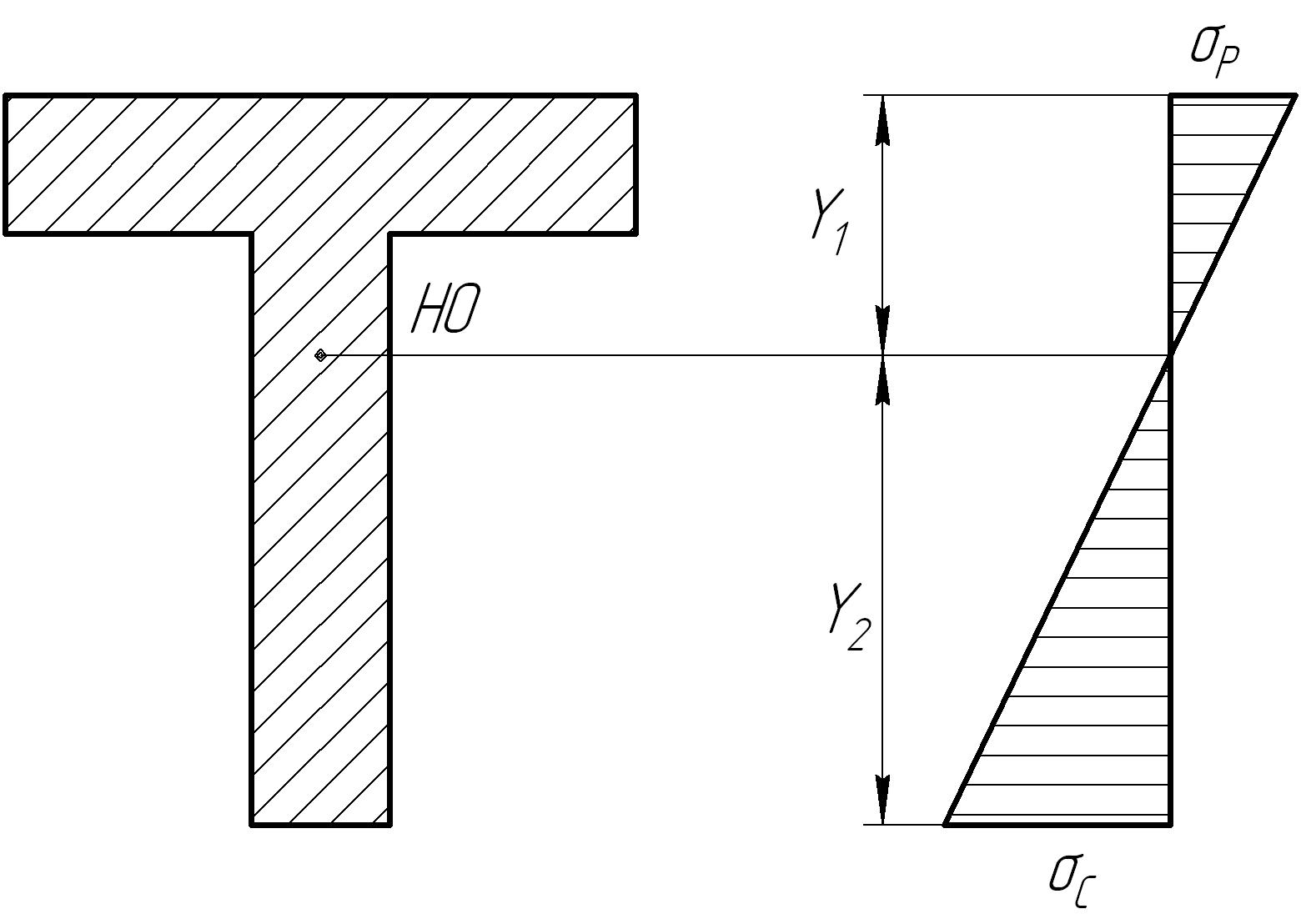
Рис. 4.1

Таким образом, при расчетах балок из хрупкого материала используют два условия прочности:

Для растянутой зоны:

. (4.2)

Для сжатой зоны:

. (4.3)

Причем наилучшее использование материала происходит при форме сечения, удовлетворяющей условию:

.

При расчете балок из пластичных материалов, например из низкоуглеродистой стали или цветных металлов, допускаемые напряжения растяжения и сжатия одинаковы: . Поэтому для таких балок целесообразными являются сечения, симметричные относительно нейтральной оси (рис. 4.2), так как в этом случае наиболее удаленные точки в растянутой и сжатой зонах сечения располагаются на одинаковом расстоянии от нейтральной оси. И, следовательно:

.

Рис. 4.2

Разделим числитель и знаменатель правой части этого равенства на :

.

Величина:

,

выражаемая в м³, см³ или мм³, называется моментом сопротивления сечения при изгибе.

Для прямоугольного сечения (рис. 4.2), размеры которого , момент сопротивления:

. (4.3)

Для круглого сечения:

. (4.4)

Наиболее экономичны при изгибе такие формы сечения, при которых материал бруса расположен как можно дальше от нейтральной оси. У таких брусьев при наименьшей затрате материалов получается наибольший момент сопротивления . Поэтому и возникли профили стандартного проката (рис. 4.2), все необходимые геометрические характеристики которых содержатся в ГОСТ 8239-89 «Двутавры стальные горячекатаные. Сортамент», ГОСТ 8240-89 «Швеллеры стальные горячекатаные. Сортамент».

Таким образом, наибольшие напряжения растяжения или сжатия в симметричном относительно нейтральной оси сечения находят по формуле:

, (4.5)

и условие прочности балки из пластинного материала имеет вид:

, (4.6)

исходя из которого выполняют три вида расчетов.

Проектировочный расчет. Приняв , по изгибающему моменту в опасном сечении находят требуемое значение момента сопротивления:

.

Затем, исходя из принятой для балки формы поперечного сечения, находят его размеры.

Расчет допускаемой нагрузки выполняется при по формуле:

. (4.7)

Затем, исходя из схемы нагружения балки, находят допускаемое значение нагрузки.

Проверочный расчет. Определив максимальный изгибающий момент и момент сопротивления сечения, находят по формуле (4.5) значение и сравнивают его с .

Аналогично выполняют расчеты балок из условия прочности.

Многие элементы строительных и машиностроительных конструкций (балки, оси, валы и пр.) кроме расчетов на прочность требуют расчета и на жесткость. Условие жесткости обычно выражается неравенством:

. (4.8)

суть которого в том, что максимальный прогиб (стрела прогиба) не должен превышать допускаемого значения .

Допускаемый прогиб зависит от назначения и условий работы рассчитываемого элемента конструкции и колеблется в широких пределах. Например, для балок, валов и осей выражают в долях пролета (расстояния между опорами), т.е. принимают , где - положительное число. Например, для валов и шпинделей металлорежущих станков , а для балок и перекрытий гражданских и промышленных зданий колеблется от до .

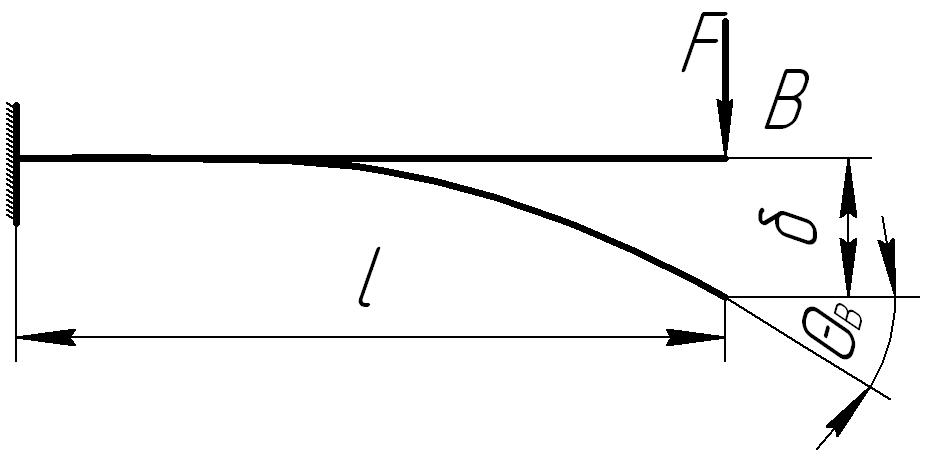
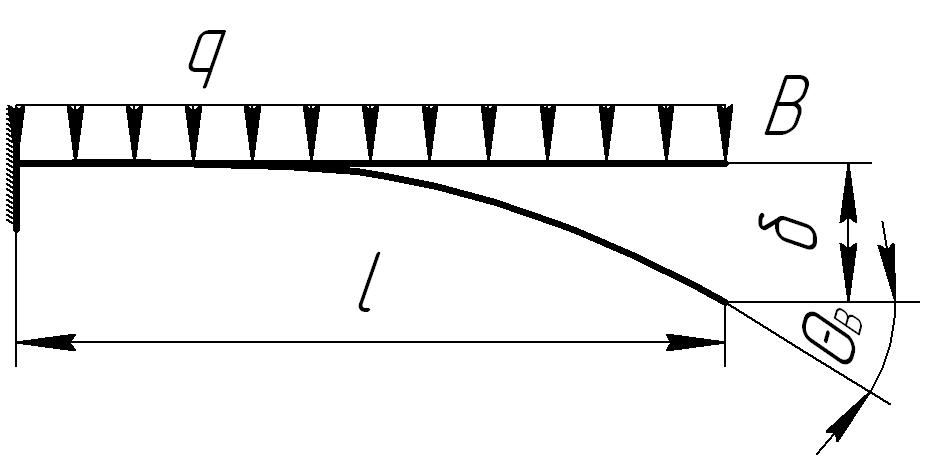
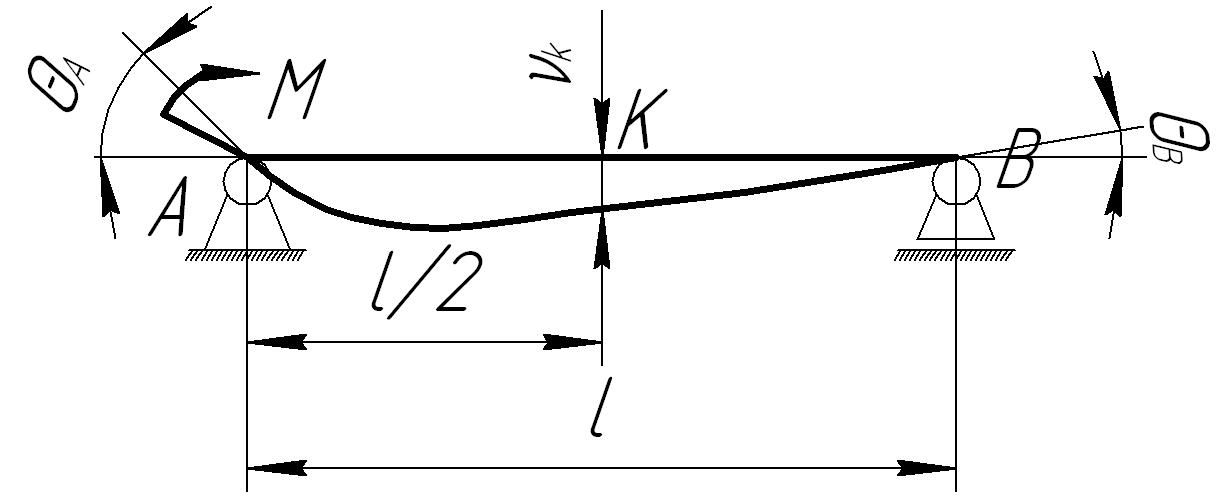
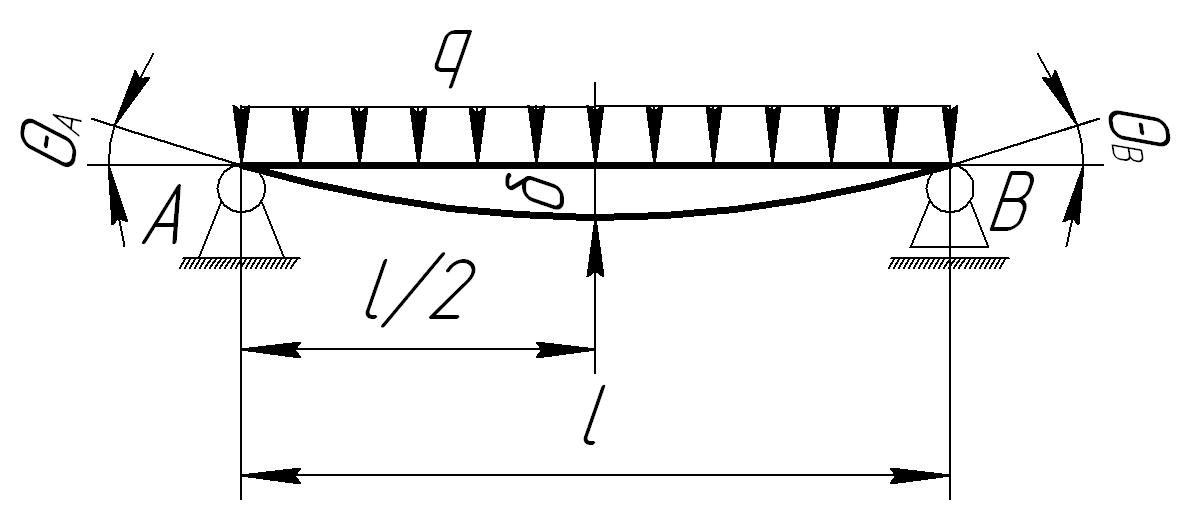
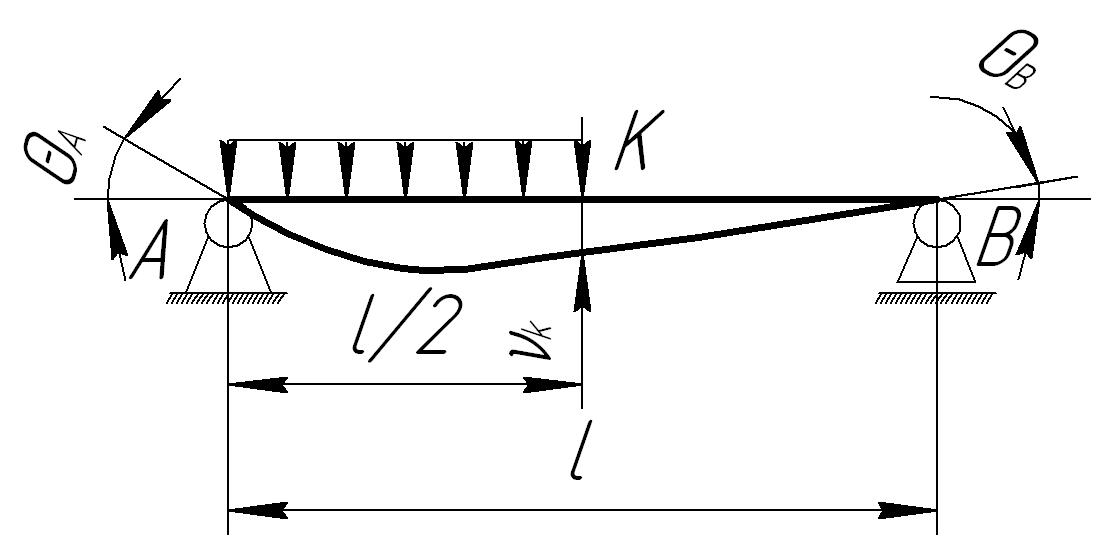
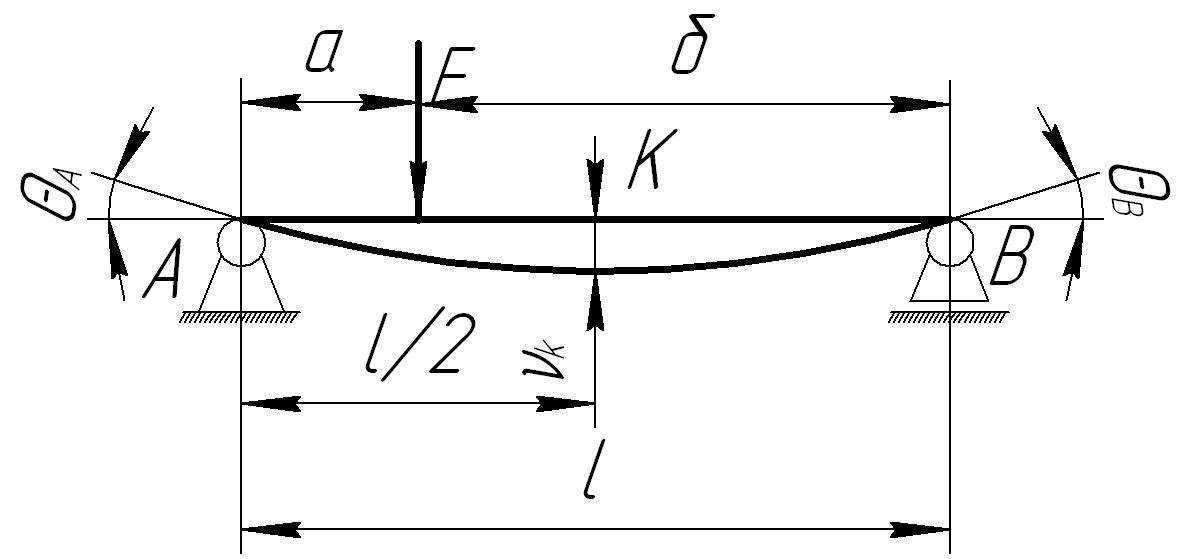
Для облегчения расчетов на жесткость используется таблица 4.1.

Таблица 4.1

№ п/п	Схема нагружения балки	Максимальный прогиб или прогиб в сечении K	Угол поворота указанного на схеме сечения
1	2	3	4
1
2
3
4
5
6
7

Продолжение таблицы 4.1

1	2	3	4
8
9
10		( )

5. Порядок решения задач

Независимо от конкретного вида конструкции задача построения эпюры внутренних силовых факторов решается в определенной последовательности:

5.1. Составление расчетной схемы

Расчетная схема выбирается следующим образом. Составляется схема объекта исследования. Объектом исследования может быть вся конструкция (например, стержневые конструкции - рамы) или часть конструкции (например, зуб шестерни). Схема объекта, как правило, составляется из брусьев, оболочек или пластин. На схему объекта наносится схема заданных (известных) внешних нагрузок и схема реакций опор (неизвестных внешних нагрузок).

В сопротивлении материалов чаще всего встречается три вида опор.

а) Шарнирно-подвижная опора в плоской системе всегда дает одну реакцию, направленную перпендикулярно к поверхности опоры катка. Шарнирно-подвижная опора обозначается в виде (рис. 5.1.1).

Рис. 5.1.1 - Схематическое изображение шарнирно-подвижных опор:

а) на чертежах; б) на расчетных схемах

б) Шарнирно-неподвижная опора. Шарнирно-неподвижная опора в плоской системе дает две реакции, так как препятствует перемещению в параллельном и перпендикулярном направлениях относительно плоскости (подошвы) опоры. Но в частных случаях шарнирно-неподвижная опора может дать и одну реакцию. Шарнирно-неподвижные опоры обозначены в виде (рис. 5.1.2).

Рис. 5.1.2 - Схематическое изображение шарнирно-неподвижных опор:

а) на чертежах; б) на расчетных схемах в общем случае;

в) на расчетных схемах в частном случае

в) Жесткая заделка (защемление). Жесткое защемление дает в плоской системе три реакции, поскольку препятствует линейному перемещению в точке заделки вдоль и поперек оси бруса и повороту. В частном случае, в зависимости от конкретной схемы нагружения и опор, жесткая заделка может дать одну или две реакции. Жесткая заделка обозначается в виде (рис. 5.1.3).

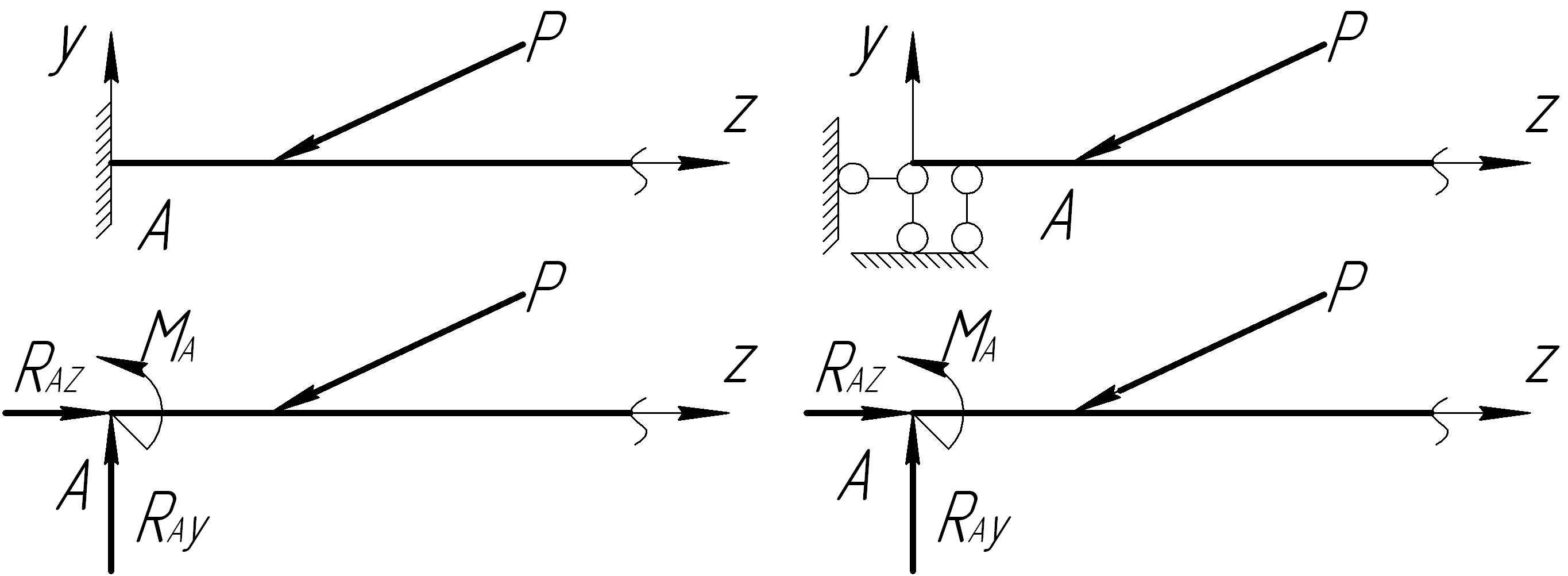
Рис. 5.1.3 - Схематическое изображение жесткой заделки:

а) на чертежах; б) на расчетных схемах

5.2. Статически определимая система и нахождение реакций опор

Ниже будет рассматриваться построение эпюр внутренних силовых факторов в статически определимых системах. Однако сам процесс определения, составления аналитических выражений построения эпюр внутренних силовых факторов в статически неопределимых системах ничем не отличается от аналогичных операций в статически определимых системах. Основное различие заключается в определении реакций опор. Если в статически определимых системах уравнений статики вполне достаточно для определения всех неизвестных реакций опор, то в статически неопределимых системах только этих уравнений недостаточно и для определения «лишних» связей применяют методы, основанные на деформационной способности системы, составляются так называемые уравнения перемещений.

Примечание: если система позволяет определить внутренние силовые факторы без определения неизвестных реакций, то задачу решают без определения реакций. Такими системами обычно являются консольные брусья.

5.3. Определение количества участков

Аналитические функции и эпюры внутренних силовых факторов строятся по участкам. Участки ограничиваются соответствующими границами. Как обычно границами участков являются точки приложения сосредоточенных внешних сил, моментов, реакций; начало и конец распределенной нагрузки; места изменения геометрической формы (рис. 5.3.1).

Замечание: При определении внутренних силовых факторов места изменения геометрических размеров поперечного сечения (рис. 5.3.1) не учитываются как границы участков, поскольку изменение поперечного сечения не влияет на величину внутреннего силового фактора. Изменение размера поперечного сечения влияет на интенсивность распределения нагрузки внутреннего силового фактора по сечению – напряжение.

Рис. 5.3.1. Схема определения количества участков при построении эпюр внутренних силовых факторов