Образование дисперсных систем

Дисперсные системы занимают промежуточное положение между макроскопическими гетерогенными системами и молекулярными растворами – гомогенными системами. Это обусловливает возможность возникновения дисперсных систем двумя путями: диспергированием макроскопических фаз (диспергационный путь образования) и конденсацией из истинных растворов или однокомпонентных гомогенных систем (конденсационное образование).

В большинстве случаев образование дисперсных систем требует затраты работы: либо подводимой извне (например, в виде механической) либо за счет протекания внутренних (в том числе и химических) процессов в самой системе. Возникшие дисперсные системы являются термодинамически неравновесными и требуют для своего существования специальной стабилизации. В противном случае система оказывается неустойчивой, в ней не может сохраняться какой-либо стабильный размер частиц или распределение частиц по размерам. Частицы самопроизвольно укрупняются, что приводит к разрушению дисперсной системы вплоть до разделения ее на макрофазы. Такие термодинамические неравновесные (неустойчивые) дисперсные системы называются лиофобными.

В отличие от лиофобных существует класс дисперсных систем, способных возникать в результате самопроизвольного (т.е. без затраты подводимой извне механической работы) диспергирования макроскопической фазы. Такие дисперсные системы термодинамически равновесны и не нуждаются в дополнительной стабилизации. Их называют лиофильными.

Основы термодинамики дисперсных систем

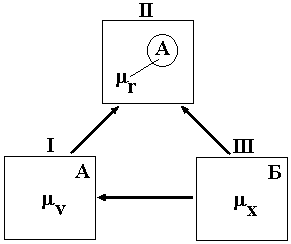
Рассмотрим процесс образования дисперсной системы путем диспергирования (дробления) макрофазы на примере отщепления одной сферической частицы радиусом r от макрофазы A., находящейся в равновесии (рис. 1). Этому процессу соответствует

Рис. 1. Термодинамика образования частицы дисперсной фазы

переход от состояния I к состоянию II. Образование частицы при постоянных давлении и температуре (P=const, T=const) требует затрат работы, равной изменению термодинамического потенциала Гиббса. Для перехода I  II требуется только затрата энергии на образование новой поверхности c площадью  (работа диспергирования) Wd, т.к. не изменяется агрегатное состояние и химический состав фазы A. (1) Химический потенциал вещества в состоянии II -  r, выше аналогичного в состоянии I -  v на величину

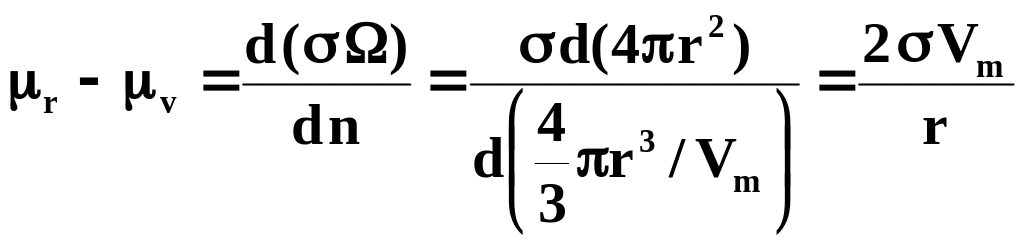
где V_m – молярный объем вещества,

n – число молей в сферической частице радиуса r.

К этому же соотношению можно прийти, умножая капиллярное давление на молярный объем ( ), считая вещество несжимаемым.

В случае образования дисперсной фазы с изменением ее агрегатного состояния или химического состава (по сравнению с исходной макрофазой) – IIIIII, т.е. наличием фазового перехода (IIII) (например, возникновение капель жидкости в паре или другой жидкости, появление кристалликов в расплаве или растворителе) выражение для работы образование фазы (равная по величине работе когезии W_c) можно записать как

(2)

где

Это уравнение (W_фаз) более универсальным и из него может быть получено выражение для W_d при учете отсутствия фазового перехода БА (IIII).

Таким образом, работа образования частиц дисперсной фазы из иного макрофазного агрегатного состояния или химического состава отличается от аналогичного, но «безфазового» перехода на величину химической работы, которая зависит от разности химических потенциалов в макроскопических фазах A и Б, и связана с энергией фазового перехода.

В самом общем случае  , но часто при зарождении новых фаз (например, при кристаллизации) в условиях равновесия состояний III и II  . В этом случае выражение для работы образования частиц принимает вид

(3)

Это соотношение (впервые полученное Гиббсом) показывает, что при условии равновесия частицы и маточной среды работа образования частицы составляет только третью часть от работы образования ее поверхности

тогда как оставшиеся две трети компенсируются химической работой, связанной с энергетической выгодностью фазового перехода. Учитывая это, общее выражение для W_фаз можно записать

(4)

при это выражение превращается в (3), а при — в уравнение (1).

Выше рассмотрены термодинамические соотношения при образовании дисперсных систем как единичный акт отделения одной частицы дисперсной фазы. Переход к оценке происходящих изменений свободной энергии в системе, содержащей множество частиц, требует учета их числа. Роль теплового движения частиц, как фактора образования и устойчивости коллоидных систем впервые была рассмотрена М. Фольмером, а в дальнейшем развита П. Ребиндером и Е.  Щукиным, где дано последовательное рассмотрение роли энтропийного фактора.

Если состав или агрегатное состояние фазы при диспергировании не изменяется, то общее изменение свободной энергии F (при P = const и V = const) – изохорно-изотермического потенциала можно записать в виде

где  - общая площадь поверхности образовавшихся частиц.

Изменение внутренней энергии складывается из затрат на разрыв межмолекулярных связей при образовании новой поверхности раздела (эндотермический процесс) и выигрыша энергии за счет сольватации (экзотермический процесс). Если разность этих двух процессов достаточно мала, то прирост энтропии (S > 0) может скомпенсировать ее, т.к. система переходит к наиболее вероятному равномерному распределению агрегатов дисперсной фазы коллоидных размеров в системе. Процесс образования коллоидной системы окажется термодинамически выгодным, т.е. F < 0. Так как

где n – число частиц размера r;

k – константа Больцмана;

 - безразмерный коэффициент равный 15÷30 для частиц сферической формы в системе с r = 10^-8 м и содержанием дисперсной фазы ~ 0,1 %.

Следовательно, условие самопроизвольного диспергирования (дробления) для частиц может быть записано следующим образом

где _{частицы} – площадь поверхности частицы размером r.

Для сферических и кубических частиц площади поверхности соответственно следующие

где r и a – радиус сферы и размер ребра куба.

Это условие имеет простой физический смысл: если частицы имеют коллоидные размеры, а межфазное поверхностное весьма натяжение мало, то самопроизвольное отщепление частиц от макрофазы оказывается возможным, поскольку работа, затрачиваемая на образование новой поверхности, компенсируется выигравшем энергии в результате участия образующихся частиц в тепловом движении. (Диспергирование не доходит до отдельных молекул, если  в этом процессе начинает возрастать в области, близкой к молекулярным размерам.)

Критическое значение поверхностного натяжения _кр. (удельной свободной поверхностной энергии), ниже которого возможно самопроизвольное диспергирование равно

где  - коэффициент формы частиц, а d – линейный размер частицы.

Для частиц размера 10^-8 м _кр. при комнатной температуре составляет десятые или сотые доли Дж/м². Эта величина (~ 0,01 Дж/м²) и называется критерием самопроизвольного диспергирования объемных фаз (критерий Ребиндера).