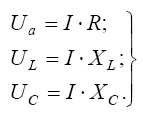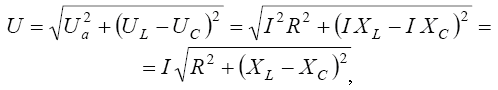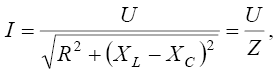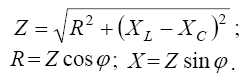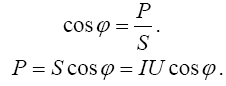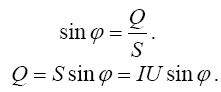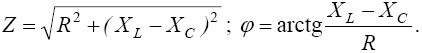Анализ неразветвленной цепи переменного тока

Цепь с активным сопротивлением, индуктивностью и емкостью представляет собой общий случай последовательного соединения активных и реактивных сопротивлений (рис. 9).

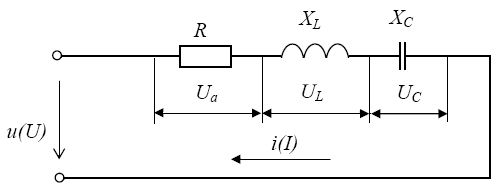
Рис. 9.

При прохождении тока в цепи на каждом элементе возникает падение напряжения:

(25)

Для каждого элемента цепи угол сдвига по фазе между током и напряжением имеет свое значение. Вектор приложенного к схеме напряжения U определится как сумма векторов напряжений на отдельных элементах схемы. Для рассматриваемой одноконтурной схемы в соответствии со вторым законом Кирхгофа справедливо уравнение

(26)

Для анализа работы данной цепи построим векторную диаграмму (рис. 10). Перед построением выбирается масштаб для тока и напряжения. Построение векторной диаграммы начинают с вектора той величины, которая является общей для всех элементов цепи. В данном случае при последовательном соединении общей величиной для всех элементов цепи является ток. Поэтому первым проводим вектор тока. Вектор напряжения на активном сопротивлении совпадает по фазе с вектором тока. Вектор напряжения на индуктивном сопротивлении опережает вектор тока на угол 90º, а вектор напряжения на емкостном сопротивлении отстает от вектора тока на угол 90º.

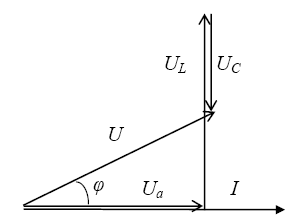
Рис. 10.

Знак перед углом сдвига фаз φ зависит от режима цепи. Если в рассматриваемой цепи преобладает индуктивное сопротивление, то

UL>UC.

(27)

В этом случае нагрузка имеет активно-индуктивный характер, а напряжение U опережает по фазе ток I (угол φ положительный).

Если в цепи преобладает емкостное сопротивление, то

UL<UC.

(28)

В этом случае нагрузка имеет активно-емкостный характер, а напряжение U отстает по фазе от тока I (угол φ отрицательный).

Выделим из векторной диаграммы треугольник напряжений (рис. 11), из которого следует:

, .

(29)

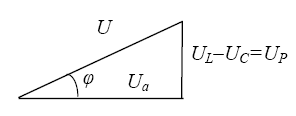Рис. 11.

Закон Ома для неразветвленной цепи запишется в виде

(30)

где Z – полное сопротивление неразветвленной цепи,

(31)

Если стороны треугольника напряжений разделить на силу тока, получится треугольник сопротивлений; если стороны треугольника напряжений умножить на силу тока, получится треугольник мощностей 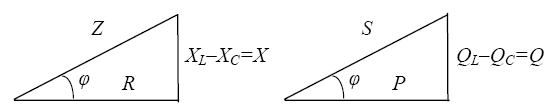(рис. 12).

Рис. 12.

Из приведенных треугольников можно записать уравнения, которые широко используются при анализе электрических цепей.

(32)

Из треугольника мощностей:

(33)

где S – полная мощность; Р – активная мощность; Q – реактивная мощность;

S=UI.

(34)

Размерность полной мощности – вольт-ампер (ВА); размерность активной мощности – ватт (Вт); размерность реактивной мощности – вольт-ампер реактивный (ВАр).

Величина cos φ называется коэффициентом мощности цепи.

	(35)
	(36)

Полное сопротивление может быть представлено комплексным числом в алгебраической и показательной форме. Комплекс полного сопротивления в алгебраической форме

(37)

где j – мнимая единица (j² = − 1).

Комплекс полного сопротивления в показательной форме

(38)

Где