Контрольні питання

1. Що розуміють під дифракційною решіткою?

2. Принцип дії гоніометра.

3. Для яких променів кут дифракції в спектрі т-го порядку більший - для фіолетових чи червоних?

4. Як впливає значення сталої дифракційної решітки на дифракційний спектр?

5. Одержати умову дифракційного максимуму при умові, що світло падає під кутом до дифракційної решітки.

6. Від чого залежить роздільна здатність дифракційної решітки?

Лабораторна робота №8

Вивчення дифракції фраунгофера від однієї щілини

Мета роботи: Вивчити розподіл інтенсивності в дифракційній картині від вузької щілини при спостереженні в світлі лазера.

Обладнання: джерело світла; оптичний квантовий генератор; (He-Ne)- лазер; розсувна щілина типу спектральної щілини; скляний матовий екран; фоторегістратор-фотодіод з електронним підсилювачем і мікроамперметром.

Теоретичні відомості

Дифракційна картина спостерігається в паралельних променях, які отримують за допомогою оптичних систем-коліматорів. При використанні лазера оптична система значно спрощується, так як випромінюючі лазером когерентні світлові пучки є паралельними і це не потребує застосування оптичних систем для їх колімації.

Схема спостереження дифракції Фраунгафера від однієї щілини зображена на рис.1. Паралельний пучок від (He-Ne) - лазера 1 падає нормально (перпендикулярно) на щілину 2, довжина якої набагато більша від її ширини b. Згідно принципу Гюйгенса кожна точка площини щілини, до якої дійшло світлове коливання, стає джерелом вторинних хвиль, які розповсюджуються в усі сторони, тобто світло дифрагує при проходженні через щілину. Дифраговані пучки є когерентними та можуть інтерферувати при накладанні. Результат інтерференції в вигляді періодичного розподілення інтенсивності спостерігається на екрані 3, який розташований на відстані від щілини 2.

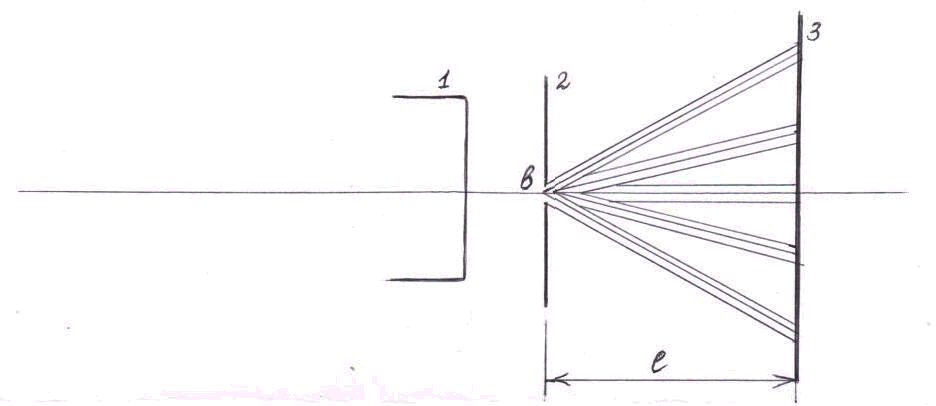
Рис.1

Розподіл інтенсивності в одержаній картині визначається додаванням елементарних хвиль, що прийшли в дану точку екрану від усіх елементів щілини, з врахуванням їх амплітуди та фази по принципу Гюйгенса-Френеля.

При невеликих кутах дифракції найбільш легко розрахувати інтенсивність графічним методом, застосованим Френелем. Для цього розіб’ємо відкриту частину хвильового фронту в площині щілини на вузькі смужки – зони рівної ширини, паралельні краям щілини.

В даному випадку фронт хвилі в площині щілини співпадає з хвильовою поверхнею, тобто фаза в усіх його точках однакова. Кожна зона (смужка) буде грати роль елементарного вторинного джерела хвиль.

Коливання від кожної зони має однакову амплітуду і відстає від попереднього коливання по фазі на одну й ту ж саму відстань , яка залежить від кута дифракції , який визначає напрям на точку спостереження. При  = 0 різниця фаз  рівна нулю і векторна діаграма має вигляд, зображений на рис. 2а. Амплітуда результуючого коливання А₀ рівна алгебраїчній сумі амплітуд додаваних коливань.

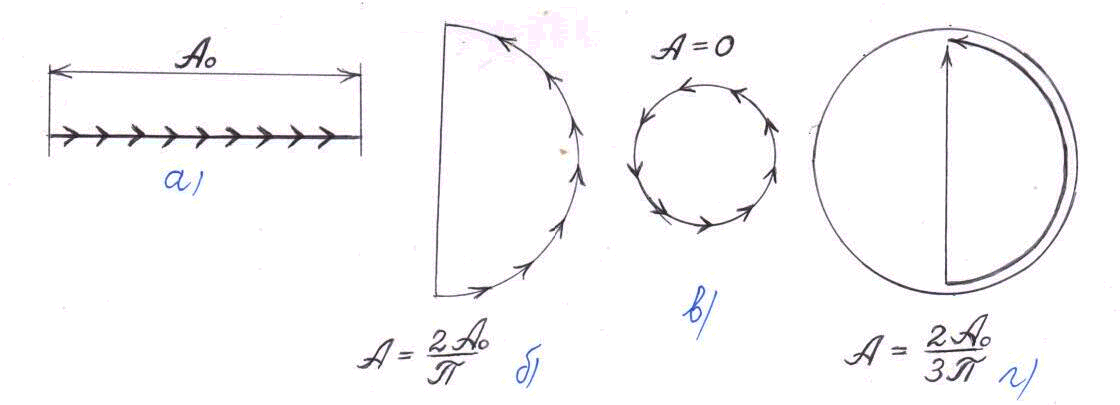
Рис.2

Якщо різниця фаз додаваних коливань, відповідних краям щілини, дорівнює  (тобто різниця ходу ), то вектори розмістяться вздовж півкола довжиною А₀ (рис. 2,б). Отже, для результуючої амплітуди отримуємо значення . В випадку, коли  = bsin =  коливання від країв щілини відрізняються по фазі на 2. Відповідна векторна діаграма дана на рис. 2,в. Вектори розташовуються вздовж кола довжиною А₀. Результуюча амплітуда рівна нулю, що відповідає першому мінімуму.

Мінімуми відповідають напрямам b sin =n, де n – ціле число.

Перший максимум спостерігається при . В цьому випадку коливання від країв щілини відрізняється по фазі на 3.

Будуючи послідовно вектори , ми обійдемо півтора рази коло діаметра (рис. 2,г).

Таким чином, амплітуда А₁ першого максимума складає від амплітуди А₀ нульового максимуму, а інтенсивність .

Аналогічно можна знайти й відносну інтенсивність інших максимумів.

Так як графічний розрахунок є наближеним, то отримані співвідношення також будуть наближеними.

Таким чином, центральний нульовий максимум значно перевищує за інтенсивністю інші максимуми. Йому відповідають приблизно 90% усього світлового потоку, що виходить з щілини. Неважко бачити, що нульова амплітуда буде відповідати кутам дифракції _к, при яких

b sin_к = +k , (1)

де k = 1,2,3 … - порядок дифракційного мінімуму.

Отже, (1) буде умовою дифракційного мінімуму. При k = 0, як видно, _к = 0 і умова b sin₀ = 0 буде умовою центрального максимуму нульового порядку.

Для аналітичного розрахунку інтенсивності в різних напрямках напишемо вираз хвилі, і підсумуємо дію всіх елементів. Амплітуда хвилі, зумовленої таким елементом, пропорційна його ширині dx, тобто дорівнює cdx. Множник с визначається з умови, що в напрямку  = 0 амплітуда хвилі, яку посилає вся щілина, дорівнює А₀, тобто cb = А₀ або . Отже, світлове збурення у відповідній дільниці щілини виразиться співвідношенням .

Щоб відшукати дію всієї щілини в напрямі, що визначається кутом  з початковим напрямком, треба врахувати різницю фаз, яка характеризує хвилі, що приходять від різних елементів до пункту спостереження В (рис. 3).

Рис. 3

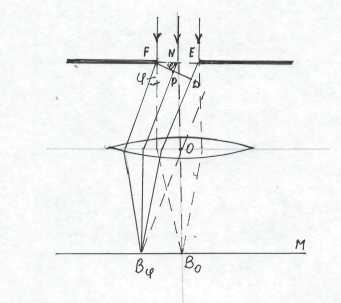
Проведемо площину FD, перпендикулярну до напрямку діафрагованих променів. Розподіл фаз, який матиме місце на цій площині, визначає собою співвідношення фаз елементарних хвиль, що збираються в точці В, бо лінза не вносить додаткової різниці фаз. Отже, досить визначити різницю ходу, що виникає на шляху від площини FЕ до площини FD. З рис.3 видно, що різниця ходу між хвилями, які йдуть від елементарної зони при точці F (край щілини) і від будь-якої точки N (яка лежить на відстані х від краю щілини), є NP = x sin. Світлове збурення в точці Р площини FD виразиться через

, (2)

де – хвильове число.

Результуюче збурення в точці В визначиться як сума цих виразів, тобто виразиться інтегралом по всій ширині щілини (по всіх значеннях від 0 до b). Отже:

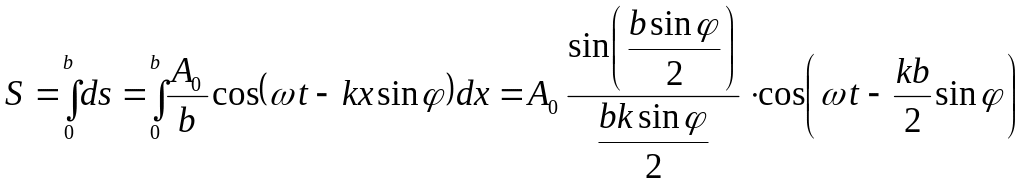. (3)

Таким чином , результуюча хвиля, що йде в напрямку , має амплітуду:

. (4)

У багатьох практичних випадках, зокрема при спостереженні в трубу, кут  настільки малий, що можна пропустити sin  , так що

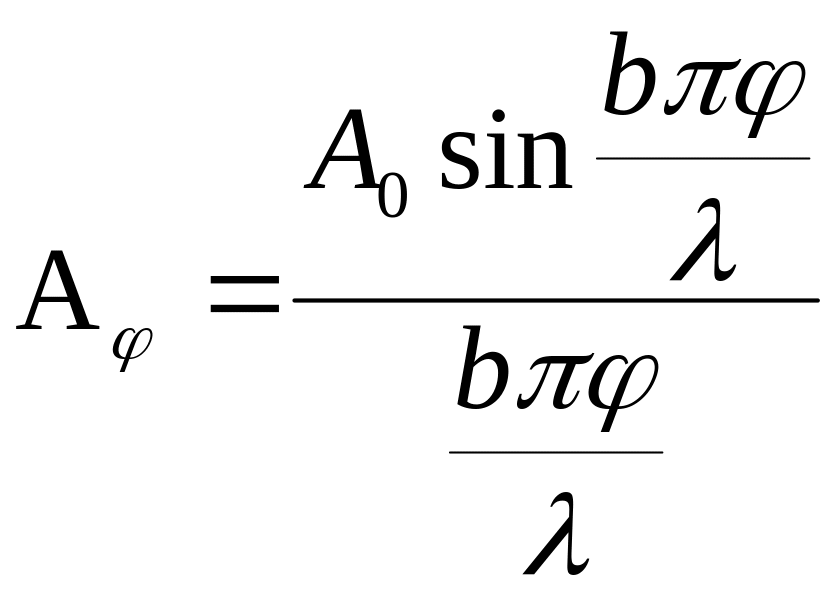. (5)

Вираз амплітуди хвилі, яка доходить до екрану ММ, показує, що вздовж екрану (із зміною ) освітленість змінюється, проходячи через максимуми та мінімуми.

Дослідимо вираз (5). А_ перетворюється в нуль для кутів , які задовольняють умову , де n = 1,2,3… (цілі числа), тобто для

. (6)

Умова (6) визначає положення мінімумів. Вона збігається з умовою виведеною вище графічним способом.

При проміжних значеннях кута  амплітуда досягає максимальних значень. Найбільший максимум має місце, коли , тобто  = 0, при цьому А_=А₀.

Наступні максимуми, які значно поступаються за величиною головному, відповідають значенням , визначеним з умов:

і т.д. (7)

На рис.4 показано хід кривої А_ як функції sin (суцільна лінія). На тому самому рисунку показано криву розподілу інтенсивності (пунктирна лінія).

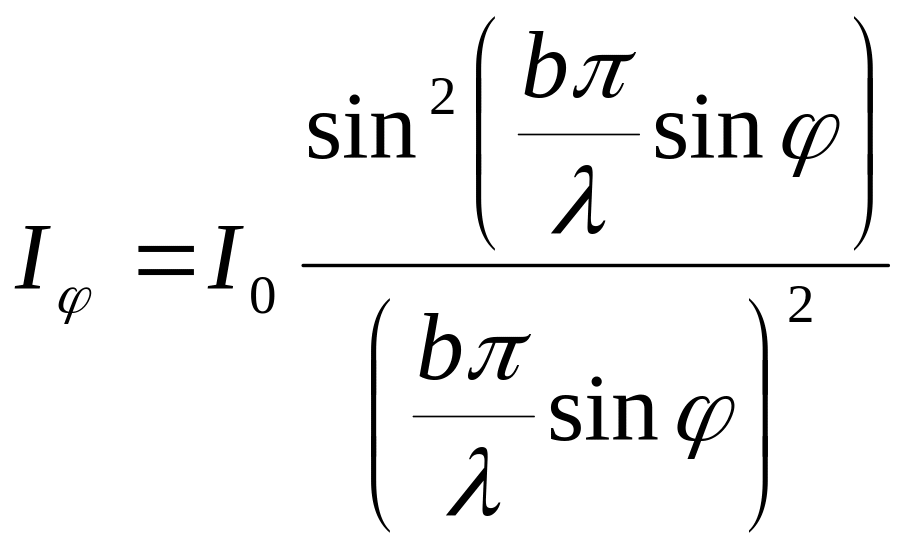, (8)

де І₀ = А²₀ є інтенсивність світла, яка йде від щілини в напрямі первинного пучка.

Як видно з рис.4 величина вторинних максимумів швидко спадає. Числові значення інтенсивностей головного і наступного максимумів відносяться як 1:0,045:0,016 і т.д., наближено це відношення можна подати у вигляді:

і т.д.

Рис.4

Спостерігаємість дифракційної картини Фраунгофера залежить від ширини щілини, а також від відстані l від щілини до екрана 3.

Якщо, наприклад, ширина щілини b = , то sin₁ = 1, а значить , тобто жодного дифракційного мінімуму спостерігатися не буде, екран буде увесь освітленим – більше в середині і менше до країв. Це відповідає чистій дифракції без інтерференції. При малих кутах дифракції картина може стати дуже малою для спостереження.

В даній роботі пропонується скласти схему дифракції від щілини, яка дозволяє чітко спостерігати дифракційну картину і побудувати експериментальний графік розподілу інтенсивності.