Случайная величина

Случайной называется величина, которая в рез-те испытания может принять то или иное возможное значение, неизвестное заранее, но обязательно одно.

Св, множество значений которой заполняет сплошь некоторый числовой промежуток, называется непрерывной. Если множество возможных значений св конечно, то такая св назыв. дискретной. Если св не относится ни к дискретным, ни к непрерывным св, то ее называют смешанной.

Каждое значение дискретной св имеет вероятность. Соответствие между всеми возможными значениями дискретной св и их вероятностями называют законом распределения св.

x	x1	x2	…	x -ряд распределения n
p	p1	p2	…	pn

При одном испытании св принимает одно и только одно постоянное значение. Поэтому события Х=x_i(i=1,2,…,n) образуют полную группу попарно независимых событий р₁+р₂+…+р_n=1.

Статистические распределения св

Функцией распределения св Х называют ф-ю F(x), Определяющую для каждого значения х, вероятность того, что св Х примет значение меньше х, т.е.

Иногда ф-ю F(x) называют интегральной ф-ей распределения.

Ф-я распределения обладает следующими св-ми:

1. Значения ф-ии распределения принадлежат отрезку

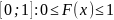
2. Ф-ия распределения есть неубывающая ф-я

3. Вероятность того, что св Х примет значение, заключенное в интервале (a,b), равна приращению ф-ии распределения в этом интервале: .

4. Если все возможные значения св Х принадлежат интервалу (a,b), то F(x)=0 при x a ; F(x)=1 при x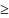 b.

5. Справедливы следующие предельные отношения:

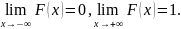
Для дискретной св Х, которая может принимать значения х₁, х₂, …, х_n, ф-я распределения имеет вид:

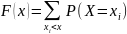
Биномиальное распределение

Является распределение k числа появлений события А при n независимых испытаниях, причем вероятность появления данного события постоянна и равна р.

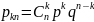
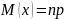
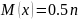
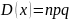D(x)= 0.25n

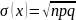
p

=q=0.5

Р

f(x)

авномерное распределение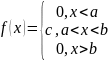

c

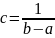
x

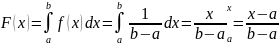
a

b

F(x)

1

f(x)

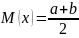
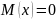
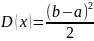
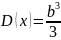
a

b

x

0

b

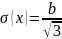
-b

Нормальное распределение

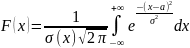
f(x)

F(x)

1

ϭ

x

x

M(x)