
- •Ошибки измерений, их виды и св-ва.
- •Оценка точности функций измеренных величин.
- •Веса функций измеренных величин. Ош. Единицы веса.
- •Общая арифметическая средина, ее вес и ско
- •Математическая обработка многократных измерений одной величины
- •Оценка точности по разностям двойных измерений
- •1)Пусть имеем ряд парных равноточных изм. . Разности двойных измерений:
- •Случайная величина
- •Статистические распределения св
- •Числовые хар-ки и моменты распределения
- •Проверка гипотезы об отсутствии корреляционной связи.
Математическая обработка многократных измерений одной величины
Если одна и та же величина измерена n раз, необходимо выполнить математическую обработку этих изм.
Выполнены неравноточные многократные изм. одной и той же величины: x1,x2,…,xn с весами p1,p2,…,pn
Окончательным,
наиболее надежным значением изм. величины
будет среднее весовое
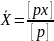 .
.
На
практике для упрощения вычислений
вводят приближенное значение изиер.
величины x0
, так, что
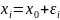 ,
где
,
где
 -
остатки.
-
остатки.
Принимают
 ,
наименьшему рез-ту изм. С учетом этого,
получим:
,
наименьшему рез-ту изм. С учетом этого,
получим:
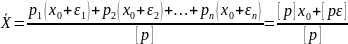
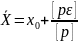
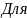 контроля вычислений
определяют ошибку округления среднего
весового. С этой целью величину
контроля вычислений
определяют ошибку округления среднего
весового. С этой целью величину
 вычисляют с двумя лишними десятичными
знаками, по сравнению с рез-ми изм. Это
будет
точ.
Округлив один запасной знак, получают
пр(принятое).
вычисляют с двумя лишними десятичными
знаками, по сравнению с рез-ми изм. Это
будет
точ.
Округлив один запасной знак, получают
пр(принятое).
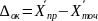 –ошибка округления
–ошибка округления
 вычисляют поправки
к рез-м изм.:
вычисляют поправки
к рез-м изм.:
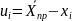
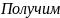 контрольную ф-лу:
контрольную ф-лу:

Умножим левую и правую части этого рав-ва на соответствующий вес и сложим по столбцам.

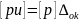 -контроль
вычисления среднего весового
-контроль
вычисления среднего весового
контрольную ф-лу
для
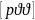 :
:
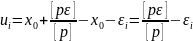
 последнее рав-во в
квадрат, умножим на веса и сложим по
столбцам:
последнее рав-во в
квадрат, умножим на веса и сложим по
столбцам:
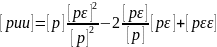
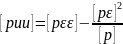 -контроль
-контроль
Оценка точности рез-в изм. производится по ф-ле Бесселя: - ско единицы веса
Оценка
точности окончательного рез-та:
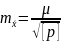 -
ско среднего весового.
-
ско среднего весового.
Оценка точности по разностям двойных измерений
В практике геод. изм. в целях контроля и повышения точности каждую величину изм. независимо несколько раз. При этом часто ограничиваются двумя изм., поэтому такие измерения называют двойными. Чем точнее выполняют двойные измерения, тем ближе будет сходимость рез-в в каждой паре изм.
1)Пусть имеем ряд парных равноточных изм. . Разности двойных измерений:
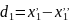
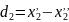


Истинные погрешности разностей равны самим разностям.
Если
 ,
то изм. разности есть ош. случайного
хар-ра. Тогда ско одной такой разности
определяется по ф-ле Гаусса:
,
то изм. разности есть ош. случайного
хар-ра. Тогда ско одной такой разности
определяется по ф-ле Гаусса:
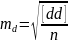 ,
где n-число
всех разностей;
,
где n-число
всех разностей;
 , то m-ош.
отдельного изм.
, то m-ош.
отдельного изм.

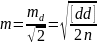
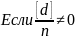 ,
то можно
предположить, что рез-ты изм. содержат
остаточную систематическую ош., которую
следует исключить из разностей двойных
изм.
,
то можно
предположить, что рез-ты изм. содержат
остаточную систематическую ош., которую
следует исключить из разностей двойных
изм.
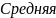 систематическая
ош. одной разности
систематическая
ош. одной разности
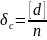 .
.
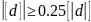
Исключив
из каждой разности двойных изм.
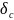 , имеем:
, имеем: , где
, где
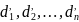 - уклонения разностей от их арифметической
середины,
они являются вероятнейшими ош. этих
разностей. Тогда ско разности двойных
изм. может быть найдена по ф-ле Бесселя:
- уклонения разностей от их арифметической
середины,
они являются вероятнейшими ош. этих
разностей. Тогда ско разности двойных
изм. может быть найдена по ф-ле Бесселя:
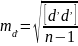 ,а ош. отдельного изм.
,а ош. отдельного изм.
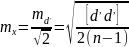 .
.
Контроль
суммы:
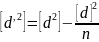 .
Ско среднего арифметического значения
двойного измерения:
.
Ско среднего арифметического значения
двойного измерения:

 имеем ряд парных
рез-в изм.
; в каждой паре рез-ты равноточны, но
каждая пара в ряде изм. неравноточна
др. парам. Разность для каждой пары изм.
будет:
имеем ряд парных
рез-в изм.
; в каждой паре рез-ты равноточны, но
каждая пара в ряде изм. неравноточна
др. парам. Разность для каждой пары изм.
будет:
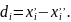 Рассматривая разности как алгебраическую
сумму величин можно написать:
Рассматривая разности как алгебраическую
сумму величин можно написать:
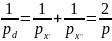 .
Поскольку разности d
можно рассматривать как истинные ош.
.
Поскольку разности d
можно рассматривать как истинные ош.
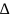 ,
то, применяя ф-лу для неравноточных
изм., получим ско единицы веса:
,
то, применяя ф-лу для неравноточных
изм., получим ско единицы веса:
 .
Тогда ско одного изм.
.
Тогда ско одного изм.
 ,
а ско среднего рез-та:
,
а ско среднего рез-та:
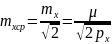 .
.
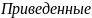 ф-лы справедливы в
случае, когда разности двойных изм. не
содержат систематических ошибок, т.е.
если
ф-лы справедливы в
случае, когда разности двойных изм. не
содержат систематических ошибок, т.е.
если
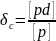 незначима. Величина
считается значимой, если соблюдается
нерав-во:
незначима. Величина
считается значимой, если соблюдается
нерав-во:
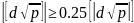
Исключив
из каждой разности двойных изм.
систематическую ош.
,
получим :
 Полученные разности
можно рассматривать как вероятнейшие
ош. изм. с весами
Полученные разности
можно рассматривать как вероятнейшие
ош. изм. с весами
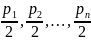 .
Тогда ско единицы веса:
.
Тогда ско единицы веса:
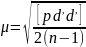 .
.
