
- •Ошибки измерений, их виды и св-ва.
- •Оценка точности функций измеренных величин.
- •Веса функций измеренных величин. Ош. Единицы веса.
- •Общая арифметическая средина, ее вес и ско
- •Математическая обработка многократных измерений одной величины
- •Оценка точности по разностям двойных измерений
- •1)Пусть имеем ряд парных равноточных изм. . Разности двойных измерений:
- •Случайная величина
- •Статистические распределения св
- •Числовые хар-ки и моменты распределения
- •Проверка гипотезы об отсутствии корреляционной связи.
Веса функций измеренных величин. Ош. Единицы веса.
Измерения, выполняемые в неодинаковых условиях, хар-ся различными ско. Поэтому за хар-ку степени доверия к результатам измерений логично принять величины, обратно пропорциональны квадрату их ско. Такая величина, хар-щая в численном виде надежность рез-та, назыв. весом измерения.
 , где
с- коэф. пропорциональности, постоянный
для всех измерений ряда, с
, где
с- коэф. пропорциональности, постоянный
для всех измерений ряда, с 0.
0.
Т.к. коэф. с может назначаться произвольно, то вес измерения явл. относительной хар-кой, дающей представление о точности этого измерения только при сравнении с весами др. изм. того же ряда. Чем больше вес изм., тем оно точнее по сравнению с др. изм.
Веса изм. обладают следующими св-ми:
Для данного ряда неравноточных изм. веса можно увеличить или уменьшить в одно и то же число раз.
Отношение весов двух изм. обратно пропорционально квадратам их ско

Для сравнения точности нескольких рядов неравноточных изм. служит ско результата измерения, вес которого принят за единицу, или ско единицы веса .
Для
ряда изм. величины xi(i=1,2,…,n)
со ско mi
примем:
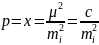
Отсюда
следует, что
 ,
что поясняет нерав-во с
0.
Тогда веса рез-в запишутся так:
,
что поясняет нерав-во с
0.
Тогда веса рез-в запишутся так:
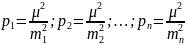
Отсюда
 , т.е. ско изм. с весом, равным единице,
равна произведению ско любого
рез-та изм. величины на квадратный корень
из его веса.
, т.е. ско изм. с весом, равным единице,
равна произведению ско любого
рез-та изм. величины на квадратный корень
из его веса.
Общая арифметическая средина, ее вес и ско
Предположим,
что проведено n
серий равноточных изм. одной и той же
величины. В первой серии выполнены изм.
искомой величины p1
раз с рез-ми
 во второй- p2
раз с рез-ми
во второй- p2
раз с рез-ми
 ,
в последней- pn
раз с рез-ми
,
в последней- pn
раз с рез-ми
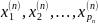 .
.
Для каждой серии изм. среднее арифметическое значение величины определяется как:

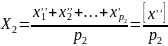
…………………………..
 , откуда
, откуда
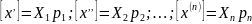
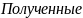 значения X1,
X2,
…, Xn
являются
неравноточными, так как получены из
разного числа измерений и имеют разные
веса.
значения X1,
X2,
…, Xn
являются
неравноточными, так как получены из
разного числа измерений и имеют разные
веса.
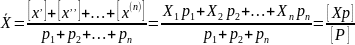
Величина называется весовым средним или общей арифметической срединой.
Таким образом, весовое среднее многократно и неравноточно измеренной величины равно сумме произведений каждого результата изм. на соответствующий вес, деленной на сумму весов.
Учитывая, что данное выражение является линейной ф-ей, для нахождения ско величины применим выражение:

 ско из выражения
ско из выражения
 .
.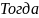 :
:
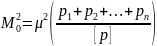 ,
,
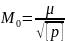
 в это выражение
,
найденное по ф-ле Бесселя, получим:
в это выражение
,
найденное по ф-ле Бесселя, получим:

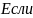 в ф-ле весового
среднего принять все веса равными
единице, то получим :
в ф-ле весового
среднего принять все веса равными
единице, то получим :
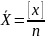 , т.е. ф-лу среднего арифметического для
равноточных изм.
, т.е. ф-лу среднего арифметического для
равноточных изм.
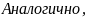 если в ф-ле
принять веса равными единице, получим
ф-лу ско среднего арифметического для
равноточных изм.
если в ф-ле
принять веса равными единице, получим
ф-лу ско среднего арифметического для
равноточных изм.
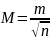
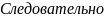 ,
ф-лы для равноточных изм. являются
частными случаями общих ф-л для
неравноточных измерений.
,
ф-лы для равноточных изм. являются
частными случаями общих ф-л для
неравноточных измерений.
Для
нахождения веса общей арифметической
средины Р0 в
выражении
примем с=1 и заменим
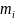 на М0.
Тогда:
на М0.
Тогда:
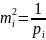 , a
, a

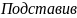 эти выражения в ф-лу
эти выражения в ф-лу
 , имеем:
, имеем:
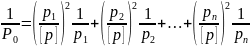
Отсюда
найдем
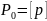 ,
т.е. вес общей арифметической средины
равен сумме весов рез-в неравноточных
измерений.
,
т.е. вес общей арифметической средины
равен сумме весов рез-в неравноточных
измерений.
Если
вес среднего арифметического
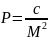 , а вес одного измерения
, а вес одного измерения
 , то на основании второго св-ва весов:
, то на основании второго св-ва весов:
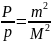 .
Поскольку
.
Поскольку
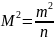 , то
, то
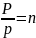 ,а P=pn
.
,а P=pn
.
Тогда при p=1 имеем P=n, т.е. вес среднего арифметического равен числу измерений.
