2. Вільні коливання в дисипативних системах з одним ступенем свободи

У реальних системах завжди відбувається процес розсіювання (дисипації) енергії. Природно, облік дисипації неминуче ускладнює аналіз коливань в динамічних системах. Різна поведінка енергії в консервативних і дисипативних системах призводить до кількісного та якісного відмінностей рухів, які в них відбуваються.

У дисипативних коливальних системах вихідний запас енергії зменшується (коливання загасають) через наявність сил «тертя». Для багатьох систем сила тертя залежить тільки від швидкості (або сили струму) і не залежить від координати (заряду). Характер такої залежності може бути різним. Розглянемо лише деякі з них.

1. Випадок сухого тертя

Сила тертя, яка не залежить від величини швидкості, а тільки від її знака, називається «сухим тертям». У ряді реальних механічних систем такий ідеалізований тип сил тертя можливий, наприклад, при русі тіла по шорсткою сухій поверхні. В електричних системах створити такий аналог сил сухого тертя не представляється можливим. З цієї причини ми не будемо проводити дослідження рухів у таких коливальних системах.

2. Випадок лінійного тертя

Лінійна залежність сил тертя від швидкості руху часто використовується в механічних системах (рис. 2.1) і описує в'язке тертя при невеликих швидкостях.

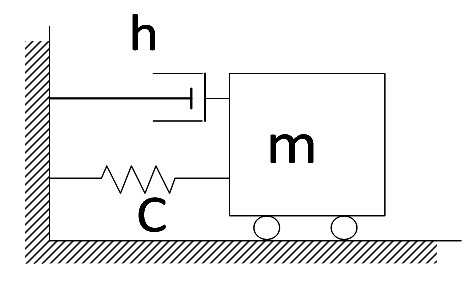
Рисунок 2.1 - Пружинний маятник з демпфером

Рисунок 2.2 – Електричний контур з опором

Для електричних систем випадок лінійного тертя відповідає наявності омічного опору (рис.2.2) при лінійності консервативних параметрів.

Диференціальне рівняння руху системи в узагальнених координатах набуде вигляду

(2.1)

Кількісне дослідження рішення рівняння (2.1) проводиться легко. Характеристичне рівняння, відповідне рівняння (2.1), має коріння

(2.2)

Розглянемо два випадки.

а) Випадок слабкого опору характеризується умовою . Корені рівняння (2.2) є комплексними:

де

Тоді загальний розв'язок рівняння (2.1) можна записати у вигляді

(2.3)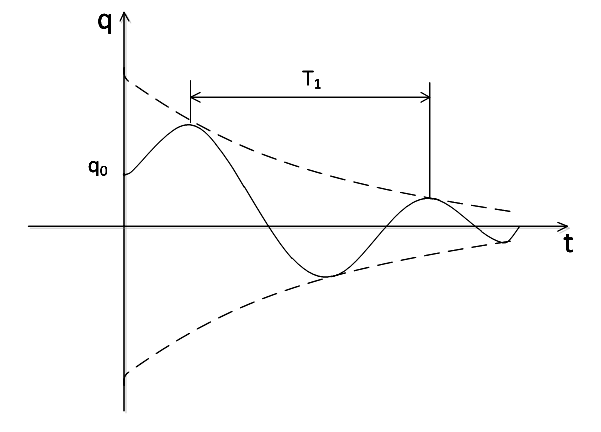

Рисунок 2.3 – Коливання лінійного слабодиссипативного осцилятора

Коливання, що відбуваються за законом (2.3), називають затухаючими коливаннями. Графік цих коливань зображений на

рис. 2.3. Огинаючі кривої процесу визначаються функціями Проміжок часу

(2.4)

прийнято називати періодом затухаючих коливань. З (2.4) випливає, що при наявності лінійної дисипації період коливань збільшується і не залежить від амплітуди.

Послідовність максимальних відхилень відповідає закону геометричної прогресії, тому що згідно (2.3)

Модуль натурального логарифма цього відношення називають логарифмічним декрементом, який служить зручною кількісною характеристикою темпу загасання вільних коливань.

б) Випадок сильного опору:

Загальне рішення рівняння (2.1) запишеться вигляді:

(2.5)

Так як коріння де завжди негативні, то рух, що описується (2.5) - неколивальний (рис.2.4). Система монотонно наближається до рівноважного стану при будь-яких початкових умовах.

Рисунок 2.4 – Графік аперіодичних рухів при сильному лінійному терті