1.5 Вільні коливання в електричному контурі з нелінійною ємністю
Розглянемо коливальний контур (рис.1.8), в якому немає лінійної залежності напруги на ємності від заряду. Такими властивостями володіють конденсатори з сегнетоелектриків. Згідно закона Кирхгофа
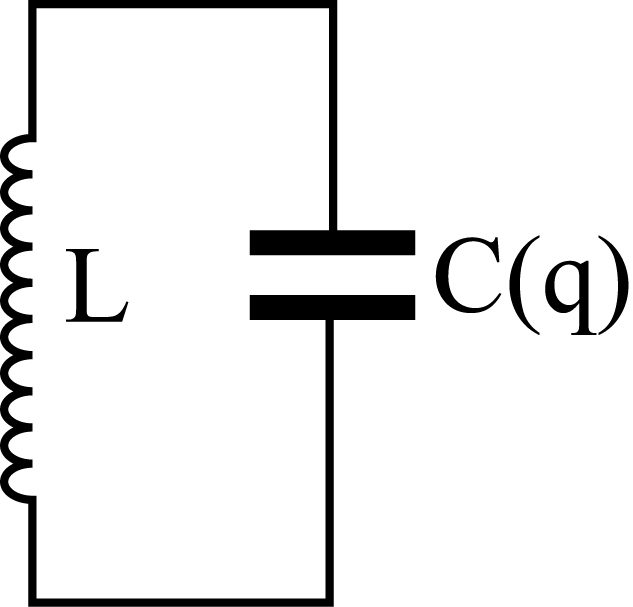
Рисунок 1.8 – Електричний контур
де
–
напруга на обкладинках конденсатора,
–
струм в системі.
Тоді для зміни заряду маємо рівняння
(1.21)
Задамося залежністю вольт-кулоновської характеристики (рис.1.9) конденсаторів з сегнетоелектриків, що часто зустрічається у формі кубічної параболи виду
(1.22)
Рисунок 1.9 – Вольт-кулонівська характеристика конденсатора з сегнетоелектриків
де
–
ємність конденсатора при
,
– коефіцієнт
нелінійності.
Рівняння (1.21) приймає вигляд:
(1.23)
де
Це рівняння відноситься до вже розглянутого раніше неліній-ного рівняння типу (1.7), тому його наближене рішення можна записати відразу
(1.24)
де
(1.25)
У цьому випадку
ми так само зустрічаємося з неізохронністю
коливань і явищем ангармонізму. Графік
(рис.1.7) залежності частоти від амплітуди
відповідає верхній кривій.
Звернемо увагу на ту обставину, що при
.
Цей результат
свідчить про недостатність використання
тільки першого наближення методу. Більше
того, якщо навіть вважати апроксимацію
точною, то при великих амплітудах
коливань перше наближення (1.24) і залежність
(1.25) стають непридатними. У цьому також
виявляється обмеженість методу
послідовних наближень.
Метод ізоклин. Фазовий портрет можна побудувати й іншим методом - методом ізоклин. Ізоклинами на фазовій площині називаються лінії, на яких нахил фазових траєкторій однаковий. Продемонструємо побудову фазового портрету методом ізоклин на прикладі нелінійного контуру.
Введемо безрозмірний
заряд
,
безрозмірний
час
,
а також позначення
Тоді рівняння (1.23) в фазових змінних прийме вигляд:
(1.26)
Рівняння сімейства
ізоклин
запишуться у вигляді:
,
де
–
довільні числа, або
(1.27)
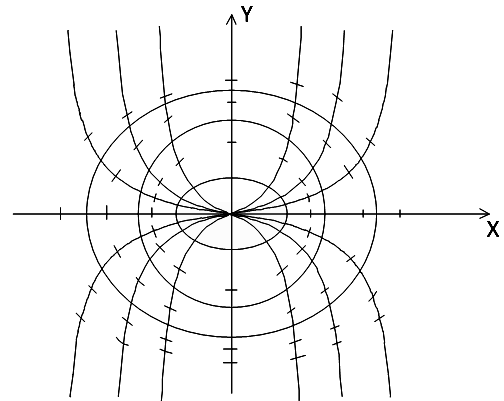
Рисунок 1.10 – Фазовий портрет контуру з нелінійною ємністю
Бачимо,
що ізоклинами є кубічні параболи з
різними коефіцієнтами
.
Виняток становлять дві ізоклини: нульова
збігається
з віссю координат
і ізоклина нескінченності
збігається з віссю координат
Ізоклини
і фазовий портрет зображені на
рис. 1.10.
1.6 Вільні коливання в контурі з нелінійною індуктивністю
З електричними системами такого типу (рис. 1.11) зустрічаємося тоді, коли в індуктивності використовуються сердечники з феромагнітного матеріалу. Крива намагнічення для феромагнетика представлена на рис. 1.12
Рисунок 1.11 – Контур з феромагнітним сердечником
Рисунок 1.12 – Крива залежності магнітного потоку від струму в котушці
де
–
магнітний потік,
–
струм, що
тече в
котушці,
–
напруженість
магнітного поля.
Користуючись рівнянням Кірхгофа
де
– число
витків котушки, які
пронизує
магнітний
потік
,
його можна написати у вигляді
(1.28)
У фазових змінних рівняння (1.28) прийме вигляд
(1.29)
де
–
постійна інтегрування.
Приймаючи
залежність
магнітного потоку
від струму
,
наприклад, за Дрейфуса
де
–
відповідні константи, можна знайти
рівняння фазових траєкторій
(1.30)
Фазовий портрет представлений на рис. 1.13, причому для малих і криві близькі до еліпсу.
Для обмеженого
інтервалу значень струму
коли величина струму не заходить далеко
в область насичення, залежність
можна апроксимувати
функцією
(1.31)
де
-
коефіцієнт самоіндукції,
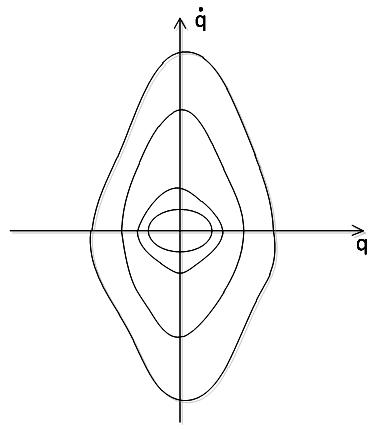
Рисунок 1.3 – Фазовий портрет контуру при залежності магнітного потоку за Дрейфуса
Рівняння фазових траєкторій тепер стане виду
яке є рівнянням
сімейства кривих, близьких до еліпсу
(особливо при малих
).
При прийнятої апроксимації (1.31) рівняння (1.28) запишеться наступним чином
.
(1.32)
Метод послідовних
наближень по
при вирішенні рівняння (1.32) з тими ж
початковими умовами
і, обмежуючись
лише першим наближенням, дає повне
рішення виду
(1.33)
Таким чином, тут отримуємо якісно ті ж особливості руху, що і в розглянутих раніше випадках. Різниця полягає лише в співвідношеннях між амплітудами кратних гармонійних компонент, причому частота рішення збільшується з ростом амплітуди.
На закінчення
відзначимо, що,
якщо криву намагнічення представити у
вигляді залежності
і прийняти у вигляді
,
то рівняння вільних коливань в контурі з нелінійною індуктивністю запишеться так:
Сімейство фазових траєкторій і сімейство ізоклин якісно співпадуть з фазовим портретом (рис. 1.10) вільних коливань заряду в контурі з нелінійним конденсатором.
КОНТРОЛЬНІ ЗАПИТАННЯ І ЗАВДАННЯ ДО РОЗДІЛУ 1
1. Поясніть переваги представлення коливальних процесів на фазовій площині.
2. Як вибирається напрямок руху зображуючої точки на фазовій траєкторії?
3. Вкажіть причини обмеженості застосування методу послідовних наближень до вирішення нелінійних систем.
4. Аналізуючи фазовий портрет (рис. 1.10) зробіть висновки щодо консервативності системи, гармонійності коливань, порушення гармонійності, швидкої зміни амплітуди струму і заряду.
5. Доведіть справедливість принципу суперпозиції для систем, описуваних неоднорідним лінійним диференціальним рівнянням.
6. Отримайте диференціальне рівняння руху перевернутого маятника.
7.
Для
ідеального маятника, описуваного
рівнянням
,
знайдіть
період коливань. Зробіть висновок.
8. Якщо в задачі 7 обмежиться лінійним рівнянням, то як зміниться вираз періоду ?