1.4 Вільні коливання систем з нелінійною відновлювальною силою. Метод послідовних наближень

У цих випадках дослідження коливань зводиться до інтегрування нелінійного диференціального рівняння. Не обговорюючи окремих випадків аналітичних рішень, познайомимося з досить поширеним методом наближеного розрахунку, званого методом послідовних наближень.

На прикладі руху маятника в рівнянні (1.1) після розкладання (1.2) функції залишимо член з (обмежуємося значеннями ). Рівняння (1.1) запишемо у формі

(1.7)

де

Приймаючи за малий параметр, будемо шукати рішення у вигляді ряду за степенями :

(1.8)

Підставляючи (1.8) в (1.7), отримаємо:

При є рішення нульового наближення, тобто рівняння

Тоді прирівнюючи до нуля суми членів розкладання при і т.п. з урахуванням попередніх рівнянь для наближень одержуємо:

(1.9)

(1.10)

(1.11)

Вибираючи початкові умови у вигляді запишемо рішення нульового наближення у вигляді Рівняння першого наближення (1.10) тепер стане:

(1.12)

Скориставшись тригонометричним перетворенням функції через кратні кути, отримуємо рівняння

(1.13)

Стандартна процедура знаходження приватного рішення, відповідного виду функції правої частини рівняння призводить до рішення

(1.14)

Очевидно, що наявність в рішенні (1.14) секулярного члена не відповідає реальному руху системи.

Причиною даного протиріччя є обрана форма приватного рішення з періодом , тобто з періодом нульового наближення, який не залежить від амплітуди коливань (так звані ізохронні коливання). Дослідження загальних властивостей поведінки маятника за допомогою фазової площини вказує на неізохронність коливань. Відхилення періоду від повинно залежати від ступеня нелінійності системи. Тому природно ввести нову частоту коливань у вигляді розкладання по ступенях :

(1.15)

де і т.п. - деякі поки невідомі величини.

Обмежимося першим наближенням в (1.15) і позначаючи знайдемо:

Підставляючи в (1.7), одержимо рівняння

Знову відшукуючи його рішення у вигляді розкладання (1.8) для нульового наближення з тими ж початковими умовами матимемо рішення у вигляді:

Рівняння першого наближення прийме вигляд:

(1.16)

або

(1.17)

Щоб у приватному рішенні цього рівняння позбутися необмежено зростаючого члена величину виберемо з умови

тобто З (1.15) тепер отримуємо:

або

Рівняння першого наближення (1.17) приймає вигляд:

(1.18)

спільне рішення якого запишемо у вигляді

де – довільні постійні.

Таким чином, повне рішення рівняння (1.7) у першому наближенні запишеться у вигляді

(1.19)

Значення і знаходяться з тих же початкових умов:

Опускаючи проміжні викладки, запишемо остаточний вид рішення

і для маятника в першому наближенні маємо

(1.20)

З (1.20) витікає:

1. Коливання неізохронні.

2. Коливання не є чисто синусоїдальними, т.к. у рішенні при- сутня третя гармоніка.

Неізохронність можна представити у вигляді графіка (рис.1.7) функції

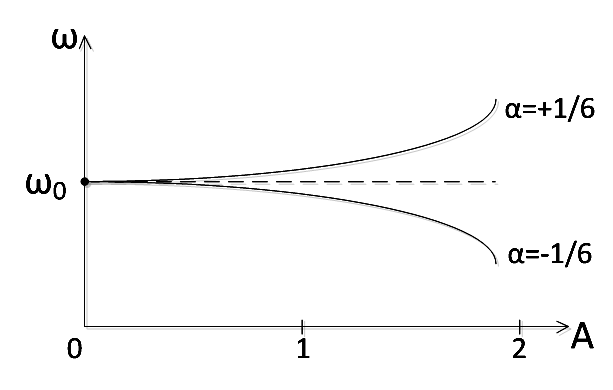
Рисунок 1.7 – Ілюстрація неізохронності коливань

Його результати можна використовувати при змінах амплітуди до в області яких справедливо прийняте розкладання функції .