8.6 Поздовжні пружні хвилі у твердому тілі

Розглянемо поширення плоскої поздовжньої хвилі в пружному циліндричному стрижні в напрямку його осі. У процесі поширення хвилі частинки стрижня отримують зміщення зі своїх рівноважних положень. Застосуємо закон Ньютона до руху елемента стрижня, укладеного між двома площинами і (рис. 8.2)

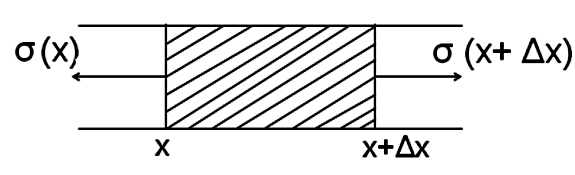
Рисунок 8.2 – Елемент стрижня з пружного матеріалу

Нехай - зміщення центру ваги виділеного елемента, тоді

, (8.9)

де - щільність середовища, - площа перерізу, - нормальне напруження, - прискорення елемента.

Розділивши рівняння (8.9) на і перейшовши до межі при , одержимо

. (8.10)

Враховуючи закон Гука і зв'язок між переміщенням і відносною лінійною деформацією , знаходимо з (8.10)

. (8.11)

Рівняння (8.11) являє собою хвильове рівняння і описує поширення плоскої пружною хвилі вздовж осі .

Швидкість поширення хвилі у твердому тілі дорівнює

, (8.12)

де Е – модуль Юнга.

8.7 Енергія пружних хвиль

Виділимо в пружному середовищі з щільністю , де поширюється плоска хвиля виду , елементарний об'єм . Завдяки хвилі обсяг набуває швидкість .

Величина кінетичної енергії речовини в обсязі дорівнює :

. (8.12)

Потенційна енергія деформації об'єму дорівнює:

. (8.13) Враховуючи (8.12) та зв'язок , матимемо величину модуля Юнга:

(8.14)

Підставляючи (8.14) в (8.13), отримаємо вираз потенційної енергії:

(8.15)

Повна енергія об'єму середовища, що приймає уасть в хвильовому процесі, дорівнює:

. (8.16)

Розділивши (8.16) на , одержимо об'ємну щільність енергії пружної хвилі:

Знайдемо середнє за часом значення об'ємної щільності енергії хвилі. Враховуючи що

,

одержимо:

. (8.17)

Таким чином, енергія пружної хвилі пропорційна квадрату амплітуди хвилі.

8.8 Перенесення енергії пружною хвилею. Енергетичні співвідношення

У процесі поширення хвиля переносить енергію з областей простору, залучених у цей процес, в області, де коливання ще не виникли. Процес перенесення енергії характеризують поняттями: потік енергії, вектор щільності потоку енергії, інтенсивність хвилі.

Кількість енергії, що переноситься хвилею через деяку поверхню за одиницю часу, називають потоком енергії :

, (8.18)

де – переносима енергія через дану поверхню за час .

Так як потік енергії в різних точках поверхні S може мати різну інтенсивність, то вводиться поняття щільності потоку енергії.

Вектор щільності потоку енергії визначається як:

, (8.19)

де – об'ємна щільність хвилі, – швидкість поширення хвилі, – одиничний вектор у напрямку поширення хвилі.

Зв'язок між вектором і потоком встановлюється з таких міркувань: за проміжок часу хвиля поширюється на відстань ; енергія , перенесена хвилею, укладена в обсязі похилого циліндра (рис. 8.3; тут довільно орієнтована елементарна площадка) дорівнює

(8.20)

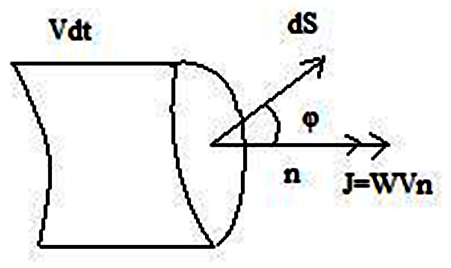
Рисунок 8.3 – Елементарний об'єм з довільно орієнтованою площею і напрямком поширення хвилі.

Запишемо (8.20) у вигляді:

. (8.21)

Враховуючи (8.21), потік енергії (8.18) стане рівним:

. (8.22)

Якщо , то рівність (8.22) дає зв'язок , де – модуль вектора потоку енергії; або

. (8.23)

З (8.3) випливає, що модуль вектора щільності потоку енергії дорівнює потоку енергії, яку переносять хвилею через одиничну площадку, перпендикулярну напрямку поширення хвилі.

Ще однією характеристикою хвильового процесу є інтенсивність хвилі. Інтенсивністю хвилі називають величину, рівну модулю середнього за часом вектора щільності потоку енергії:

. (8.24)

Враховуючи (8.19), можна отримати інше вираження для інтенсивності хвилі:

.