8.3 Інші типи синусоїдальних хвиль

Хвилі, що описуються рівнянням виду

, (8.3)

називають круговими синусоїдальними хвилями. Якщо в (8.3) r є відстані від деякої прямої розташування джерел обурення, то хвилі називають циліндричними хвилями.

Сферичні синусоїдальні хвилі описуються рівнянням

, (8.4)

де r – відстань від точки розташування в просторі точкового джерела збурень.

8.4 Рівняння хвиль в поглинаючої середовищі

До цих пір передбачалося, що хвиля поширювалася в середовищі, яке не поглинає, тобто частинки середовища здійснюють гармонійні коливання. Якщо частинки середовища в процесі руху відчувають сили опору, то коливання їх будуть затухаючими. Розглядаючи лінійну залежність сил опору від швидкості частинок (див. (2.1)), ми показали, що амплітуди коливань експоненціально зменшуються з часом. Аналогічно амплітуда хвилі експоненціально зменшується з відстанню, пройденою хвилею. Енергія коливань частинок перетворюється у внутрішню енергію речовини середовища. Такі середовища називаються поглинаючими середовищами.

Таким чином, рівняння хвиль (8.1), (8.3), (8.4) в поглинаючому середовищі матимуть вигляд:

,

,

.

Тут називають коефіцієнтом загасання хвилі.

8.5 Рівняння плоскої хвилі, що поширюється в довільному напрямі

Нехай хвильовий вектор, який вказує напрям поширення хвилі в просторі, становить з осями декартової системи координат x, y, z кути , , відповідно. Коливання часток на хвильовій поверхні x=0 (рис. 8.1) описуються рівнянням

.

Коливання часток на іншій хвильовій поверхні, віддаленій на відстані від першої, спізнюється, як відомо, за часом на величину і описується функцією

,

або

. (8.5)

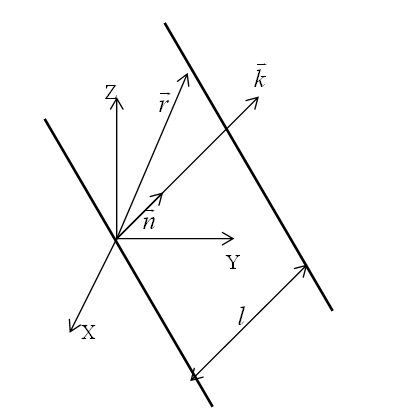
Рисунок 8.1 – Хвильові поверхні плоскої хвилі

Відстань можна представити як , де - радіус-вектор будь-якої точки розглянутої хвильової поверхні. Тепер рівняння хвилі (8.5) можна представити у вигляді

або

, (8.6)

де , , - проекції хвильового вектора на координатні осі. Таким чином, плоска хвиля, що поширюється в довільному напрямі, описується рівнянням (8.6).

Швидкість поширення фази хвилі в напрямку хвильового вектора дорівнює . Визначимо швидкість фази в іншому напрямку, наприклад, під деяким кутом до вектора . З умови сталості фази

диференціюванням по t знаходимо

,

де - швидкість в необхідному напрямку. Звідси і

. (8.7)

Тут - фазова швидкість в напрямі вектора . Аналогічно (8.7) можемо записати швидкість розповсюдження фази вздовж координатних осей x, y, z:

, , . (8.8)

З (8.8) випливає, що фазова швидкість не є вектором. Більш того, при певних значеннях кутів , , може виявитися, що відповідна фазова швидкість прийме значення більше швидкості світла. Це не суперечить теорії відносності, т.к. фазова швидкість не пов'язана зі швидкостями частинок, або зі швидкостями перенесення інших фізичних величин.