7.3. Граничний перехід до суцільного середовища. Хвильове рівняння
У параграфі 7.2 для
окремого виділеного елемента було
отримано диференціальне рівняння (7.1).
Якщо тепер вважати n
,
Рисунок 7.4 – Графік залежності циклічної частоти від хвильового числа
тобто параметри
системи розподілені по довжині струни,
то зміщення
замінюється
функцією
Визначимо зміщення сусідніх елементів:
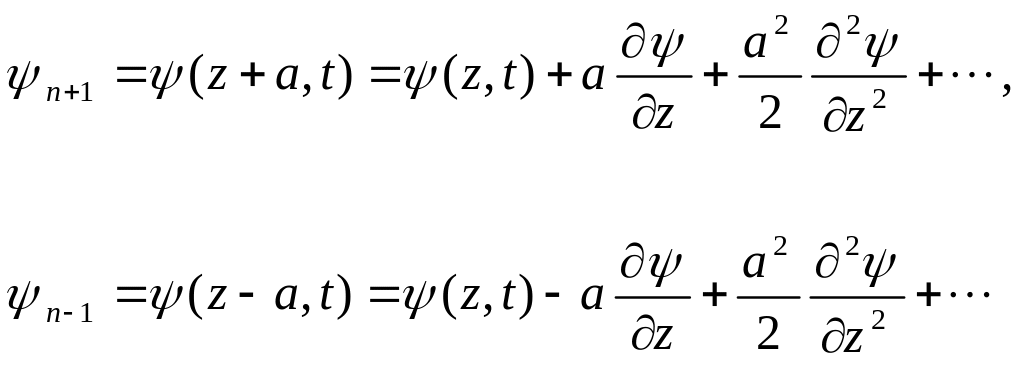(7.9)
Підставляючи (7.9) в (7.1), отримаємо найпростіше скалярний одномірне хвильове рівняння, що описує поперечні коливання струни
,
(7.10)
де
- погонна щільність струни.
КОНТРОЛЬНІ ЗАПИТАННЯ І ЗАВДАННЯ ДО РОЗДІЛУ 7
1. Наведіть приклади поздовжніх і поперечних узгоджених коливань в упорядкованих структурах.
2. Поясніть сенс дисперсійного співвідношення.
3. Покажіть, що довільні функції виду задовольняють найпростішому хвильовому рівнянню.
8 Скалярні і векторні хвилі
8.1 Початкові відомості про хвилі
Хвилею називають процес розповсюдження в просторі коливань частинок середовища. Самі частки не переміщаються в просторі обсягу середовища, а рухаються біля своїх положень рівноваги.
Залежно від того, напрямки коливань частинок середовища збігаються або перпендикулярні напрямку розповсюдження хвилі, розрізняють хвилі поздовжні і поперечні.
Фронтом хвилі називають геометричне місце точок, до яких у процесі поширення хвилі коливання доходять в один і той же момент часу. Хвильовий фронт відокремлює область простору, де частки середовища знаходяться в збуреному стані, від області, де коливання ще не виникли.
Хвильовою поверхнею називають поверхню, яка проходить через положення рівноваги частинок, що коливаються в однаковій фазі.
Хвилі називають плоскими, сферичними або циліндричними, якщо їх хвильові поверхні являють собою площини, сферичні і циліндричні поверхні відповідно. Напрямки поширення хвилі перпендікулярні хвильовим поверхням.
Нехай якась
скалярна фізична величина S (наприклад,
зсув частинок середовища) залежить
тільки від однієї просторової координати
x і часу t, тобто
.
Легко бачити, що,
якщо структура
аргументу функції
має
вигляд
,
то значення
функції
,
яке вона мала в точках площини
в момент часу t,
буде тим же в точках площини
,
але із запізненням за часом на
,
де
.
Дійсно, це підтверджується порівнянням між собою виразів:
,
.
У такому випадку
говорять, що обурення фізичної величини
S поширюється у позитивному напрямку
осі x зі швидкістю
.
Будь-яка функція
від аргументу виду
висловлює обурення поширення уздовж
осі х. Якщо графік залежності S від x має
піднесення і западини та їх розташування
різному в різні моменти часу, то процес,
що описується рівнянням,
називають плоскою
хвилею.
Хвиля, що поширюється в негативному напрямі осі x, описується рівнянням
.
8.2 Гармонійні хвилі
Хвилі, що описуються гармонійної функцією, називаються гармонійними хвилями. Рівняння плоскої гармонійної хвилі, що розповсюджується в позитивному напрямі осі x, прийнято записувати у вигляді:
.
(8.1)
Введемо визначення:
величину
називають амплітудою
хвилі,
- фаза хвилі,
-
початкова фаза; вона визначається
вибором початку відліку координати x і
часу t. Величина
є циклічна (кругова) частота коливань
частинок середовища. З періодичності
функції
за часом знаходимо
-
період коливань частинок.
Коефіциєнт
називають хвильовим
числом. Його
можна представити як
,
де v – швидкість поширення хвилі.
Відстань, на яку поширюється хвиля за час, що дорівнює періоду коливань частинок, називається довжиною хвилі :
.
Довжина хвилі пов'язана з хвильовим числом, співвідношенням:
.
Фазовою швидкістю хвилі називається швидкість переміщення в просторі поверхні постійної фази хвилі. З умови сталості фази для гармонійної плоскої хвилі (8.1) маємо:
.
(8.2)
Це рівняння є рівнянням площини у просторі. Швидкість її переміщення і є фазовою швидкістю хвилі:
.
Зазначимо, що у
разі гармонійної хвилі фазова швидкість
збігається зі
швидкістю хвилі, тобто зі швидкістю
поширення коливань частинок середовища.
Хвильовим вектором
називають вектор, який визначається
виразом:
або
,
де
-
одиничний вектор, перпендикулярний до
хвильової поверхні.