7 Коливання в впорядкованих структурах. Хвильове рівняння
7.1 Загальні зауваження
Кристалічна гратка твердих тіл представляє самий наочний об'єкт, який природно назвати упорядкованою структурою з осциляторів (коливальних елементів). Найпростішими прикладами моделі впорядкованої структури, в якій тотожні осцилятори пов'язані між собою не будь-яким, а певним чином, є одномірна гратка з однакових частинок, механічна система, що складається з набору маятників, ланцюжок пов'язаних електричних контурів, ряд однакових акустичних резонаторів, ланцюжок, утворений з магнітів і т. п.
Таким чином, ми
переходимо до розгляду систем з N
ступенями свободи, причому N може бути
дуже великим і навіть «нескінченно
великим» числом. Кожній ступені свободи
відповідає своя власна частота і форма
коливань. Часто їх називають модами
коливань.
Якщо вивести один елемент такої системи
з положення рівноваги, то будуть
зміщуватися і сусідні - по всій
впорядкованій
структурі побіжить «хвиля». Іншими
словами, при дуже великому числі елементів
у системі (у межі нескінченно великому),
укладених в обмеженому обсязі, вона
веде себе як безперервне
середовище. Таке твердження має на
увазі, що зміщення всіх елементів в
околиці точки може бути описано вектором
зміщення
,
де
- безперервна функція. Ця функція замінює
опис, що задає зміщення
,
і т.п. окремих елементів. У такому випадку
говорять про поширення хвилі. Тут слід
пам'ятати, що координати x, y, z відповідають
рівноважного стану частинок і не залежать
від часу.
Як приклад розглянемо моди коливань струни з вантажами. Під «струною» вважаємо невагомі пружини, на яких розташовані точкові маси. Послідовність таких струн показана на рис. 7.1, що дозволяє легко зрозуміти конфігурації і частоти мод.
Рисунок 7.1– Різні конфігурації і частоти мод коливань
7.2 Поперечні коливання струни з вантажами
Розглянемо
закріплену на кінцях струну з N вантажами,
кожен маси M. Відстань між вантажами –
,
натяг «пружин» в рівновазі одно
(рис.
7.2).
Сила натягу
передбачається значною, щоб можна було
знехтувати дією сили тяжіння.
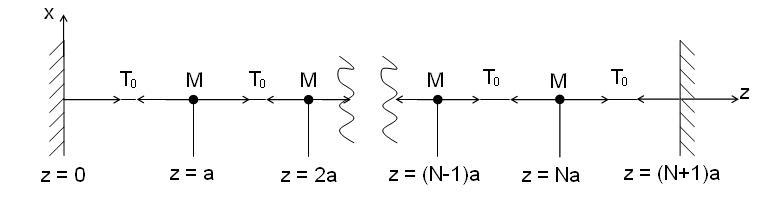
Рисунок 7.2 – Упорядкована лінійна структура пов'язаних вантажів
Обмежимося розглядом
тільки поперечних коливань вантажів
вздовж осі Х; зміщення позначимо через
.
Знайдемо рівняння руху «n» вантажу. (Схема конфігурації струни представлена на рис. 7.3). Враховуючи наближення малих коливань, закон Ньютона дає наступне рівняння руху:
.
(7.1)
Рисунок 7.3 – Схема конфігурації струни в деякий момент часу
Визначимо частоти
і конфігурації окремих мод. Припустимо,
що ми маємо моду з частотою
.
Кожен вантаж здійснює гармонійні
коливання з частотою
і
фазою
,
а форма моди визначається відношенням
амплітуд коливань різних вантажів.
Позначимо через
- амплітуду коливання n-го вантажу для
даної моди. Тоді має
(7.2)
З (7.2) знаходимо
(7.3)
Підставляючи (7.3) і (7.2) в рівняння (7.1) отримуємо
або
. (7.4)
Рівняння (7.4) визначає залежність форми коливання від частоти. Спробуємо знайти рішення (7.4) у вигляді
,
(7.5)
де
.
Тоді
і, отже,
. (7.6)
Підставляємо (7.6) в (7.4), одержимо
.
(7.7)
Припускаємо, що
(7.7) справедливо для будь-якого вантажу
n, незалежно від того чи перебуває він
чи ні в вузловій точці, тобто приймаємо
.
Отже, щоб
було рішенням рівняння (7.4), потрібно
виконання умови
,
звідки
або
.
(7.8)
Вираз (7.8), що зв'язує
частоту
і «довжину хвилі»
(див.
курс математичної фізики),
або хвильове число k для даної моди,
називається дисперсійним співвідношенням
для струни з вантажами.
На рис.7.4 показаний
графік і
для струни з п'ятьма вантажами, закріпленої
з обох кінців.