Пример решения задачи 1

По условию задачи нужно подобрать площади сечения опорных стержней, т. е. выполнить проектный расчёт. Необходимо воспользоваться условием прочности (1.1), для этого потребуются значения продольных сил N, возникающих в стержнях. Найдём эти силы.

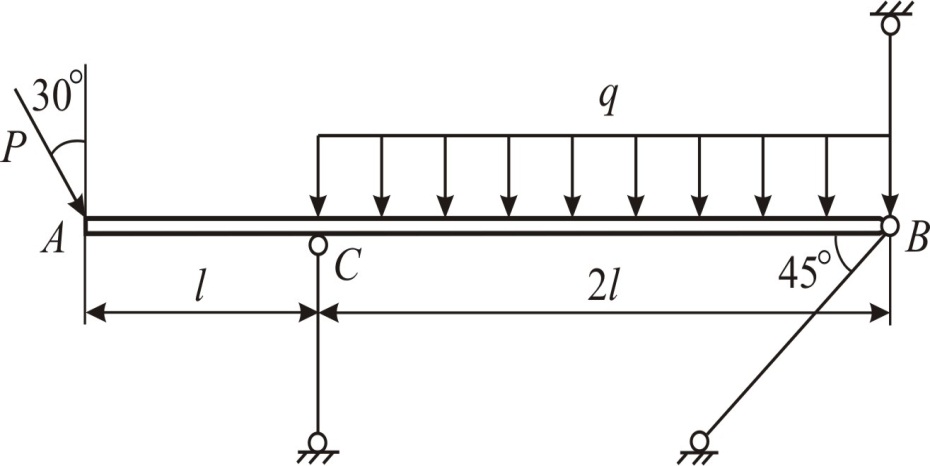
Рис. 1.3

1. Определение продольных усилий в опорных стержнях

Обозначим стержни цифрами 1, 2, 3 (рис. 1.4, а). Стержни имеют по концам шарниры, поэтому внутренняя продольная сила N направлена вдоль стержня. Так как материал стержней имеет разные значения допускаемых напряжений на растяжение и сжатие, то для составления условий прочности важно знать растянут стержень или сжат. Это оценивается направлением продольной силы. Если сила растягивает стержень, то она считается положительной, и перед её значением ставится знак « + »; если сила сжимает стержень, то она считается отрицательной, и перед её значением ставится знак « - ». Чтобы автоматически получить правильный знак силы , поставим для всех стержней направление сил , , , при котором происходит растяжение стержней.

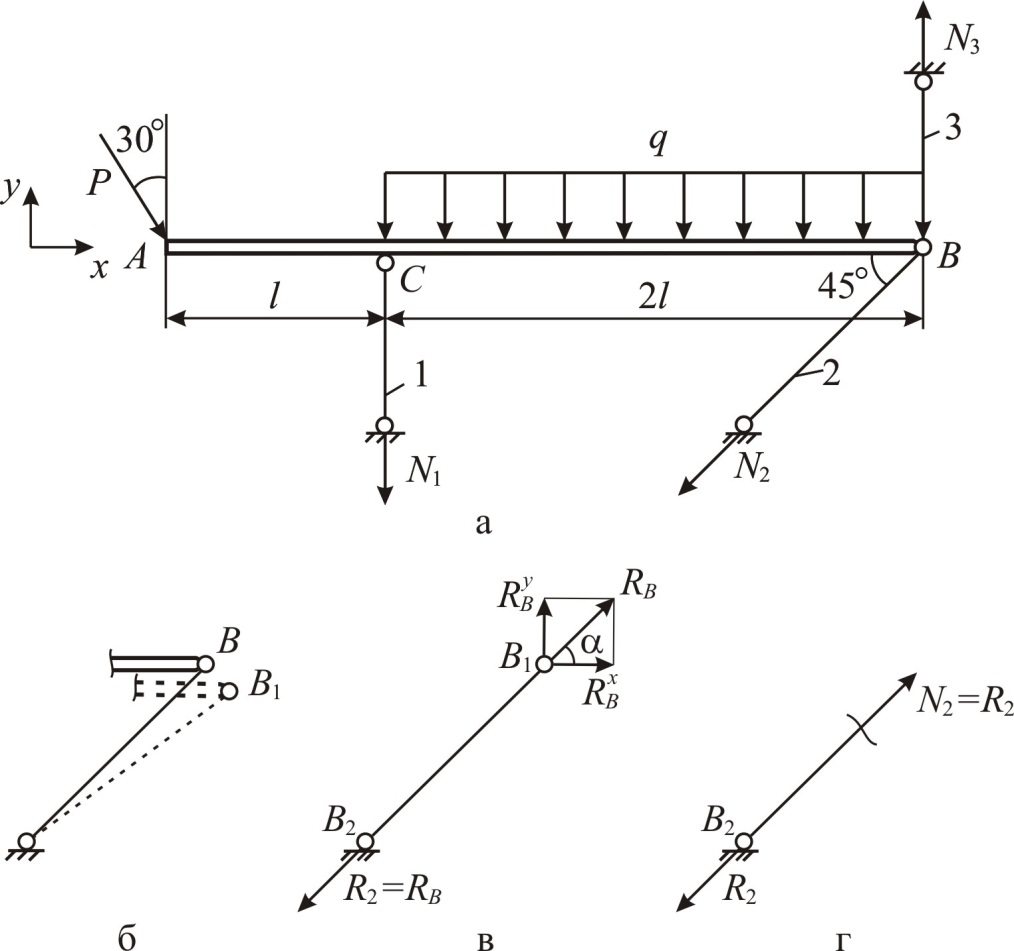
Рис. 1.4

Силы , , должны удовлетворять условиям равновесия бруса . Брус нагружен внешней нагрузкой и и неизвестными силами , , , которые в совокупности представляют плоскую систему сил, поэтому для бруса имеем три уравнения равновесия:

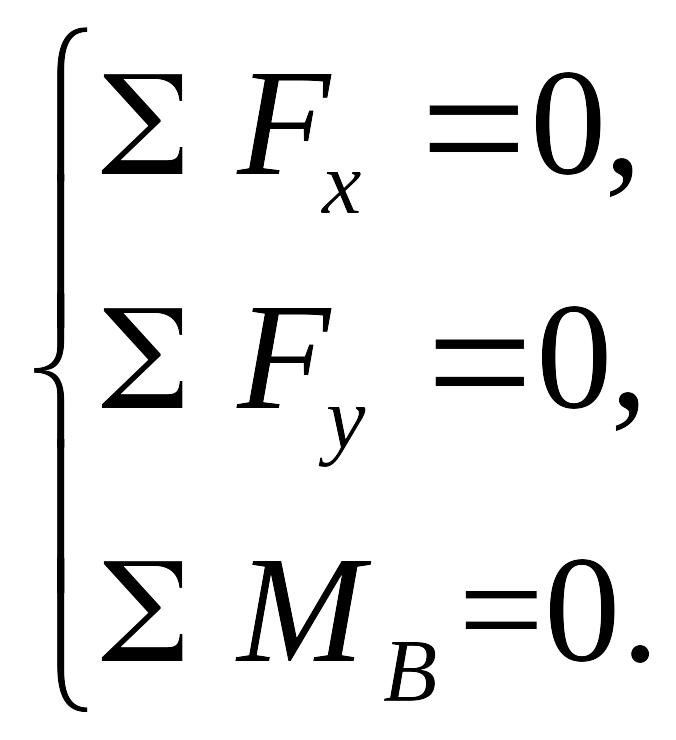
Запишем эти уравнения:

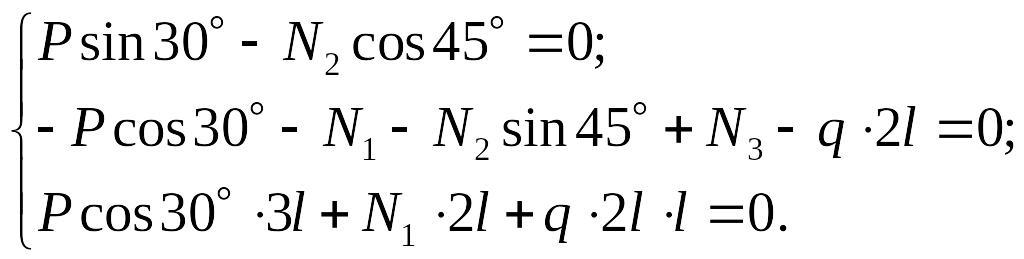
Заметим, что вычисления с целью уменьшения цифрового объёма можно выполнять через доли ql, подставляя заданное соотношение .

Из третьего уравнения

^.

_{Округляя, запишем N1 = -86,4 кН. Усилие N1 отрицательно, значит, стержень 1 сжат.}

Из первого уравнения

кН.

Продольное усилие положительно, значит, стержень 2 растянут.

Из второго уравнения

кН.

Продольное усилие положительно, стержень 3 растянут.

Для проверки правильности найденных усилий составим неиспользованное уравнение равновесия ∑ М_А = 0:

_=0,

,

Равенство нулю говорит, что усилия в стержнях найдены верно.

2. Подбор площади сечения стержней

Для подбора сечений в условие прочности по допускаемым напряжениям (1.1), нужно брать , если стержень растянут, и = ^, если сжат.

Стержень 1 сжат, условие прочности (1.1) для него принимает вид

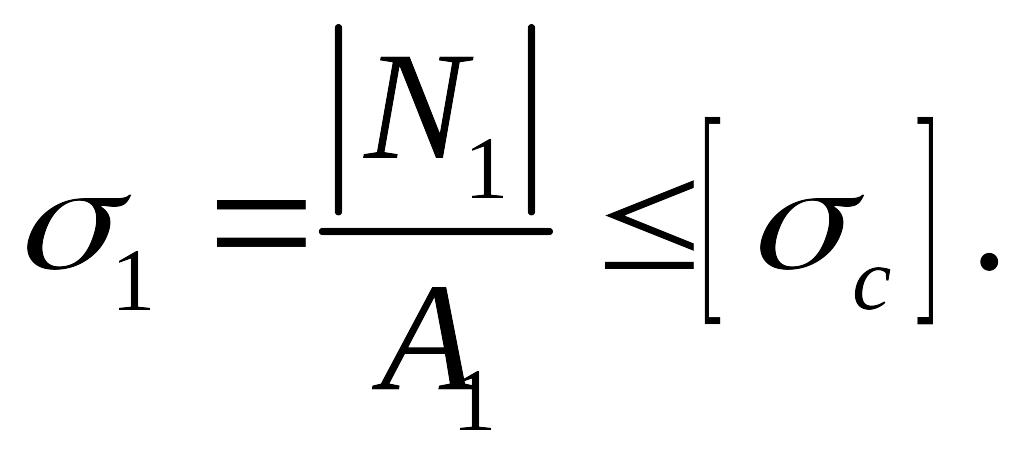
Необходимо помнить, что для сжатого стержня в условие прочности ставим модуль продольной силы. Подставляя в это условие прочности значения =86,4 кН и МПа, получаем

,

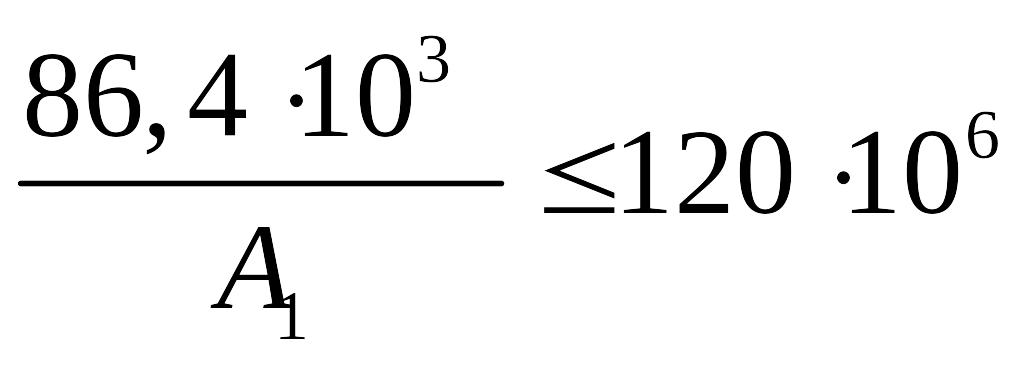отсюда площадь сечения

.

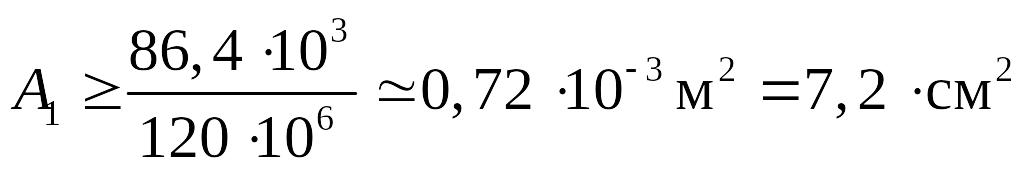Принимаем в соответствии со знаком «больше либо равно» площадь сечения 1-го стержня .

Составим условие прочности для 2-го стержня. Стержень 2 растянут, то по условию (1.1)

.

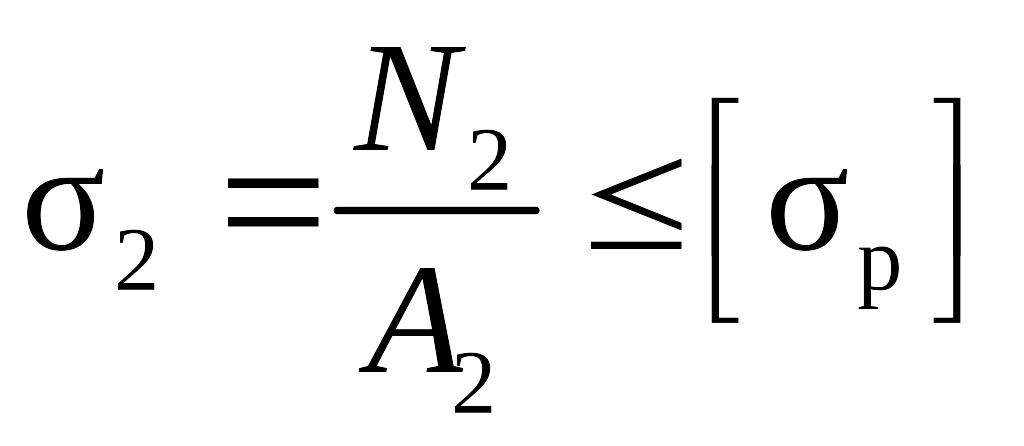Подставляя значения кН и [σ] МПа, получаем

,

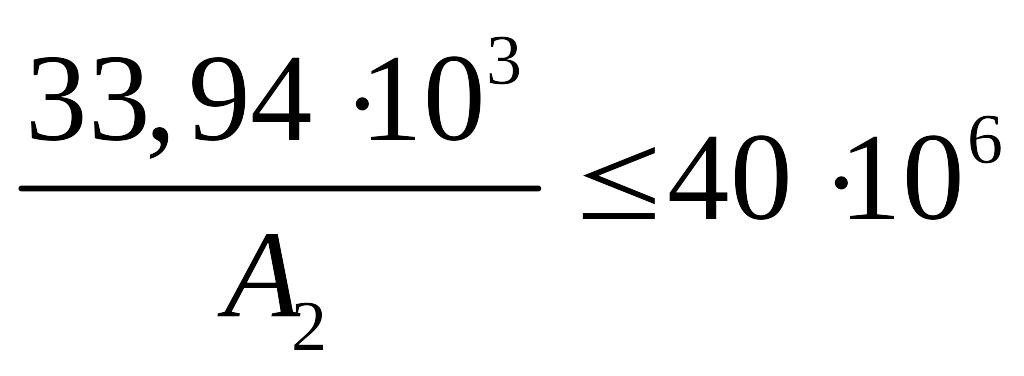отсюда требуемая площадь сечения

.= ^.

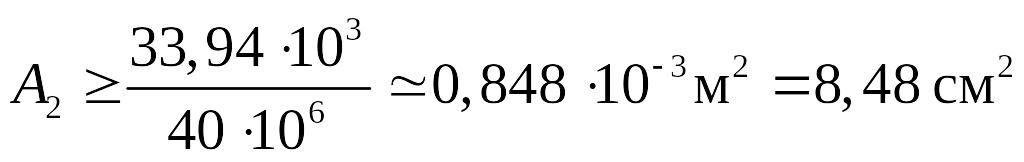Округляя, принимаем площадь сечения 2-го стержня .

Для 3-го стержня продольное усилие положительно, поэтому условие прочности (1.1) имеет вид:

^.

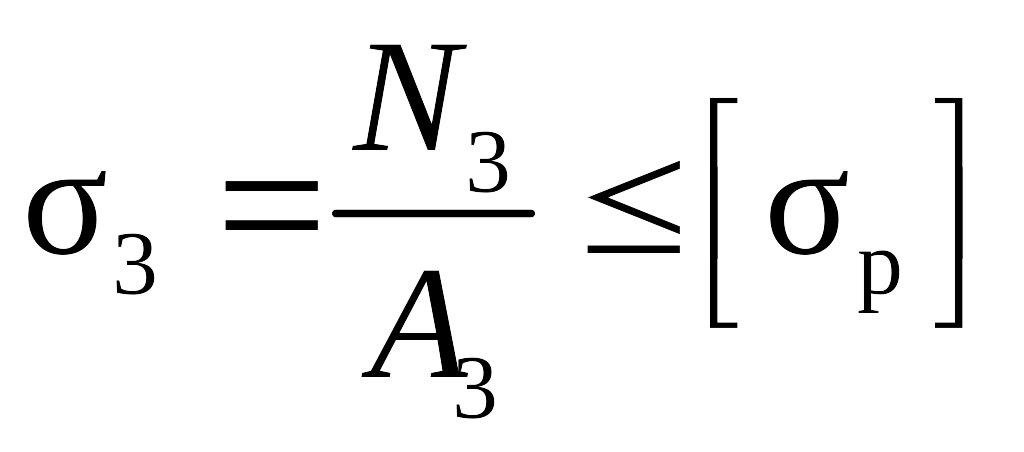Подставляя в это условие прочности значения кН и МПа, получаем

,

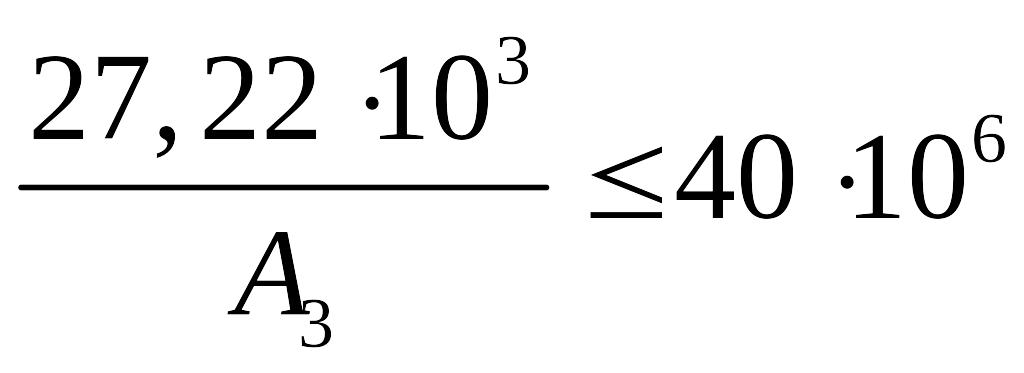отсюда требуемая площадь сечения

^.

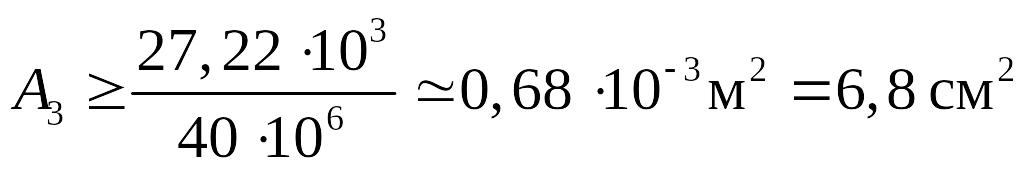Принимаем площадь сечения 3-го стержня .

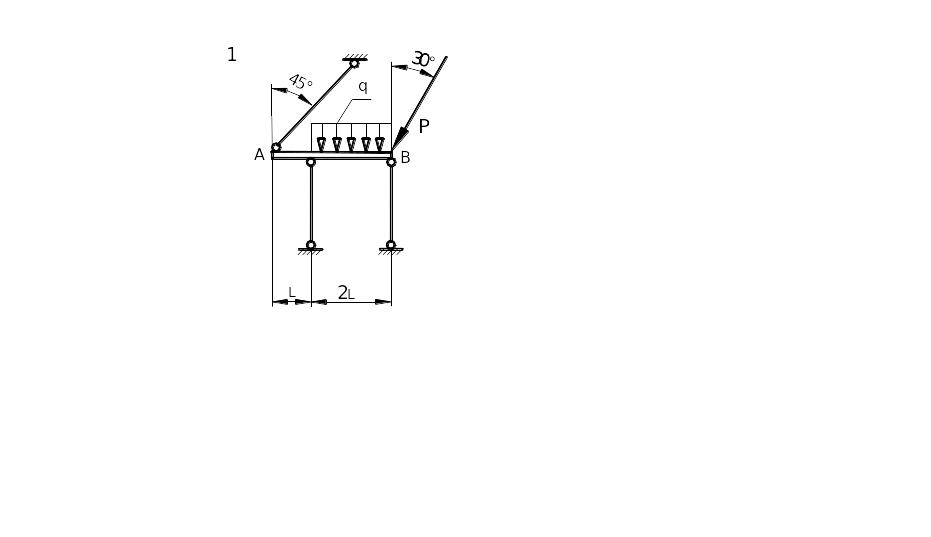
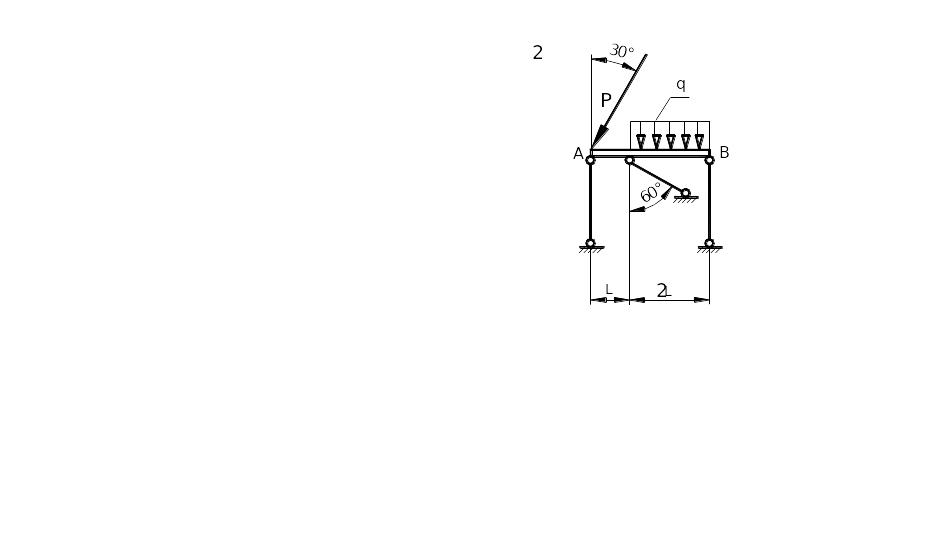
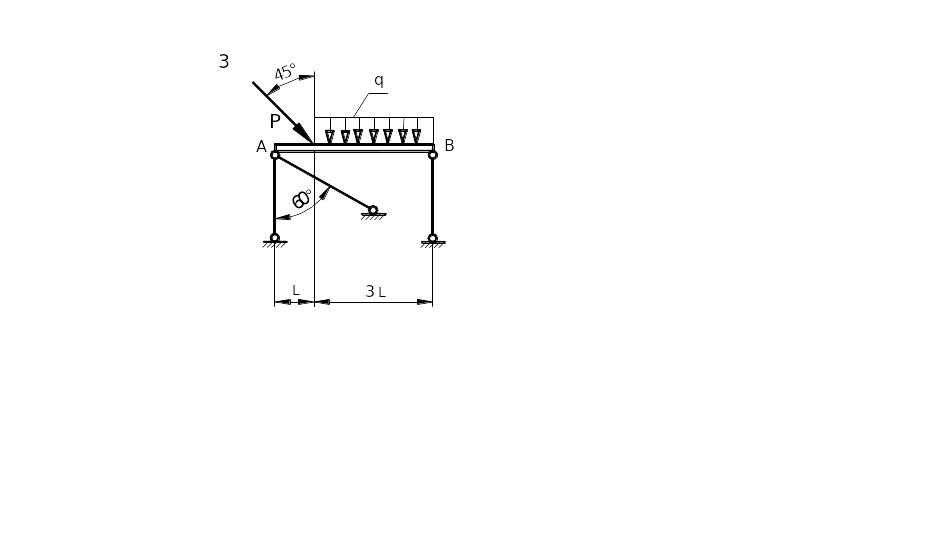
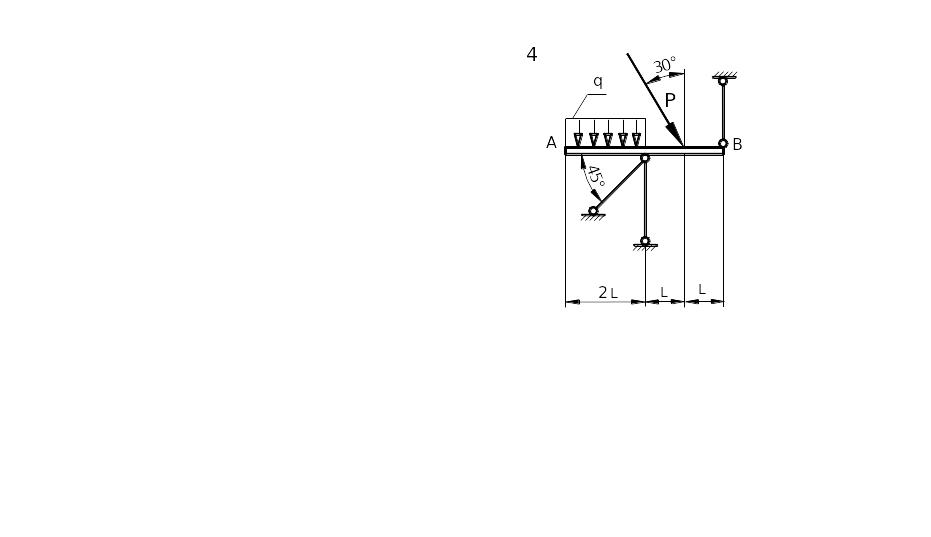
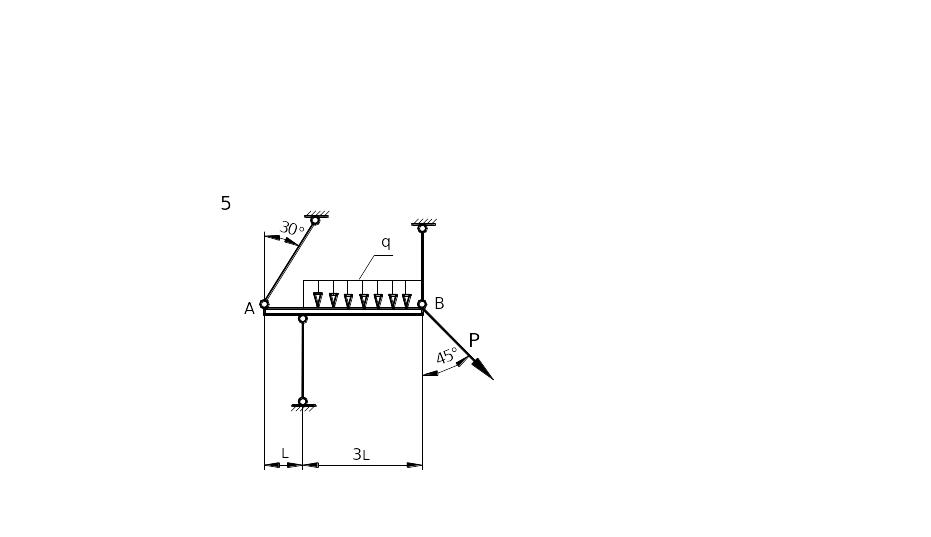
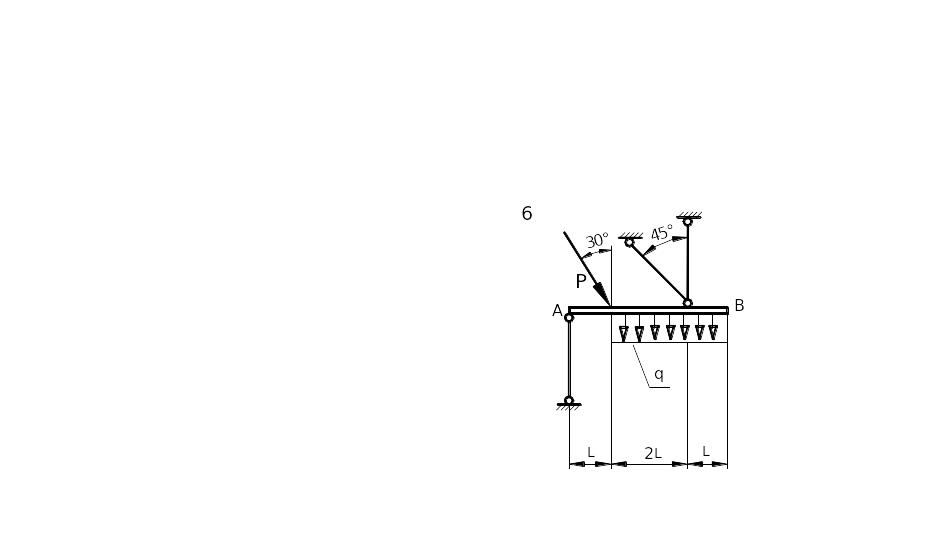
Таблица 1.1. Схемы стержневых систем задачи 1

Таблица 1.1. Схемы стержневых систем задачи 1