Пример решения задачи 8

Рассмотрим решение для рамы, представленной на рис. 8.2, а. Диаметр стержней d = 0,02 м, длина l = 0,15 м, вес груза Q=8 Н.

1.Вычисление сил инерции

При вращении рамы силы инерции от сосредоточенного груза Q вычисляем по формуле (8.1):

в сечении D

,

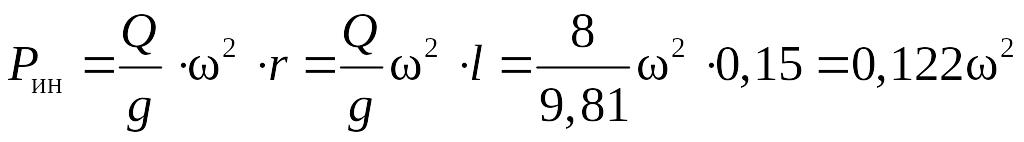в сечении К

.

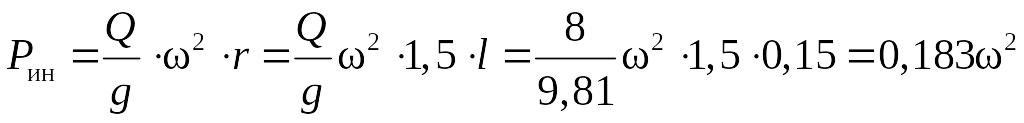2. Расчётная схема рамы

Расчётная схема рамы, на которую нанесены силы инерции (они перпендикулярны оси вращения), изображена на рис.8.2, б.

Согласно с принципом Даламбера, если добавлены силы инерции, то имеем возможность изобразить статическую схему, в которой динамические опоры представим как шарнирные, используемые в статических расчётах. Поэтому опоры А и В на рис. 8.2, б заменены на шарнирные.

3. Построение эпюр внутренних усилий

Найдём силы реакции опор А и В, составив уравнение равновесия

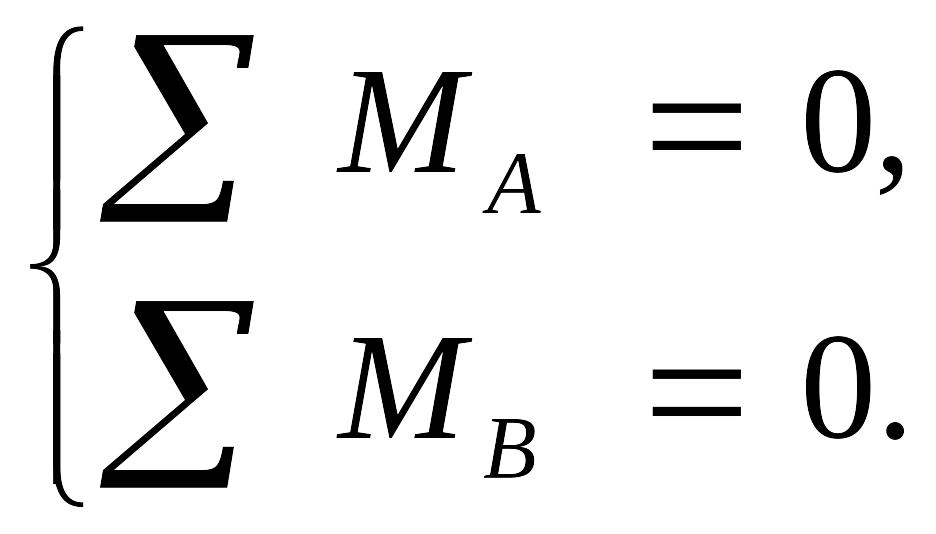
Или

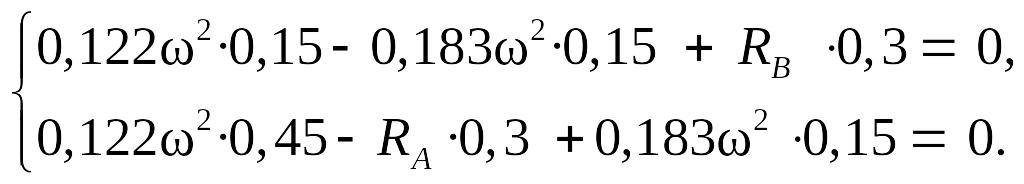
Отсюда R_А = 0,2745ω², R_В = 0,0305ω².

Проверим правильность найденных значений, используя тождество :

(0,122+0,183) ω² = 0,2745ω²+0,0305ω²

0,305 = 0,305.

Запишем выражения поперечной силы Q по участкам:

на участке АС Q = 0,122ω²,

на участке АЕ Q = 0,122ω² - 0,2745ω² = - 0,153ω²,

на участке ВЕ Q = 0,031ω².

а Заданная схема б Расчётная схема в Эпюра N г Эпюра Q д Эпюра М

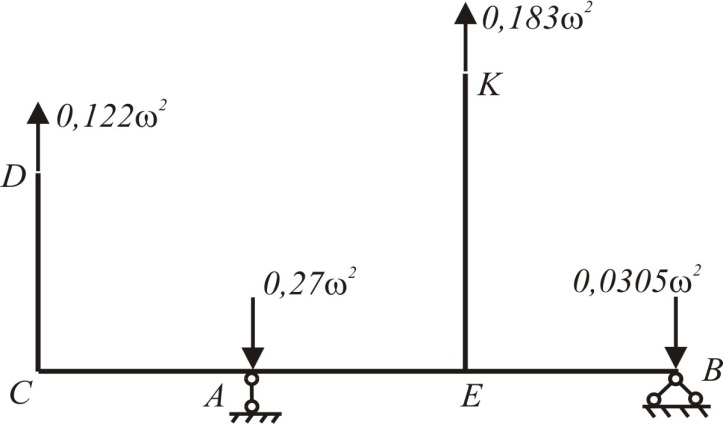
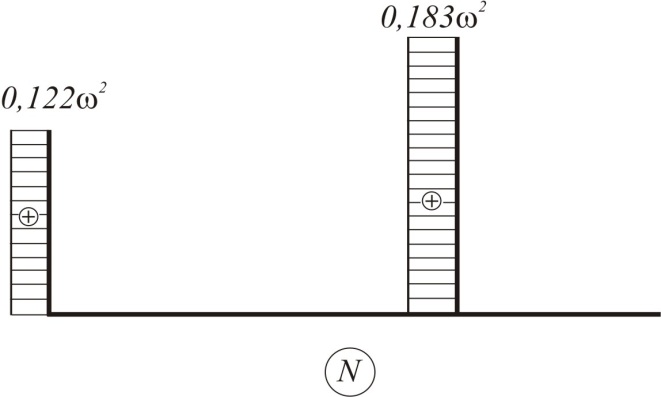
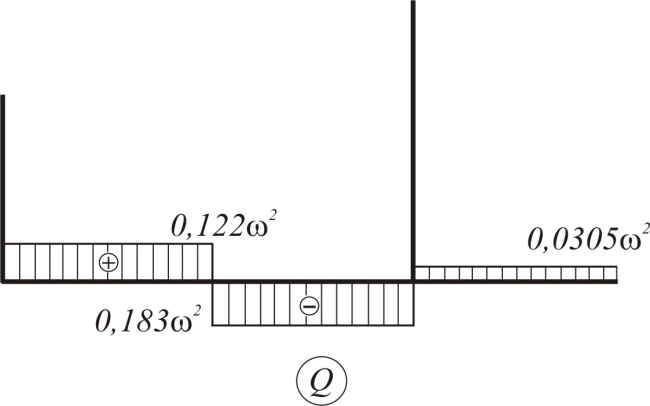
Рис. 8.2

Определим значения изгибающих моментов М в характерных сечениях С, А, Е, В:

М_С = 0,

М_А = 0,122ω²·0,15 = 0,0183ω²,

М_В = 0,

М_Е = - 0,0305ω²· 0,15 = - 0,0046ω².

Продольная сила N возникает на участке DС и КЕ:

на участке DС N = 0,122ω² , на участке КЕ N = 0,183ω².

По этим значениям, используя правила построения эпюр для плоских рам, которые рассмотрены в задаче 7, построим эпюры продольных сил N, поперечных сил Q и изгибающих моментов М (рис. 8.2, в, г, д).

Согласно эпюрам опасными могут быть: по растяжению все сечения на участке КЕ, и по изгибу − сечение А.

Составим условия прочности для этих сечений соответственно.

Для участка КЕ:

отсюда получим ω ≤ 524¹/_с .

Для сечения А:

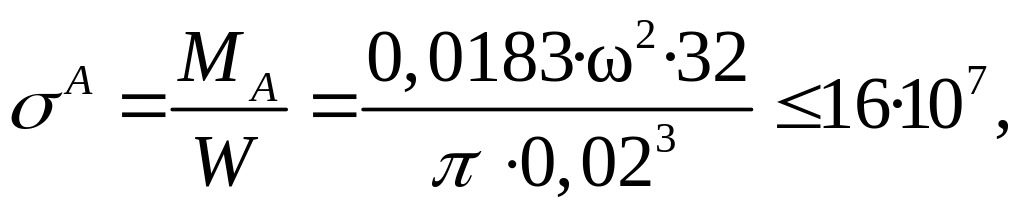
отсюда ω ≤ 82,9 ¹/_с.

За допускаемую скорость выбираем меньшее значение:

[ω] = 82,9¹/_с,

что составляет число оборотов в минуту

,

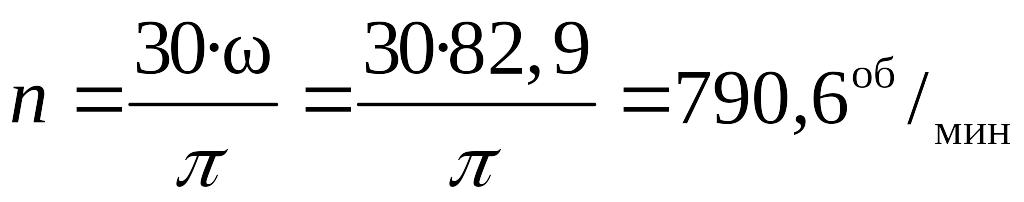тогда принимаем допускаемое число оборотов в минуту .

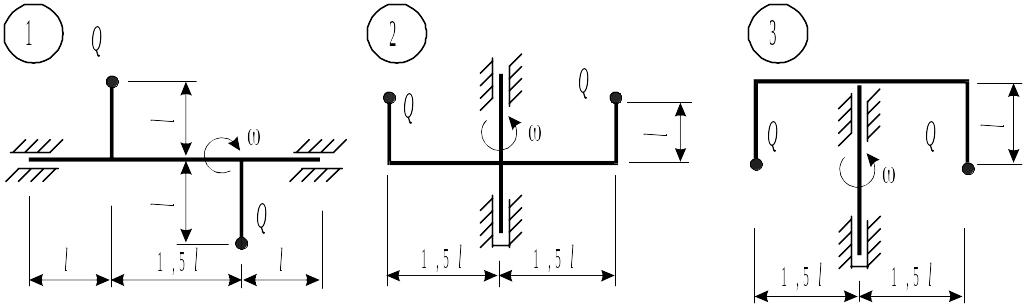
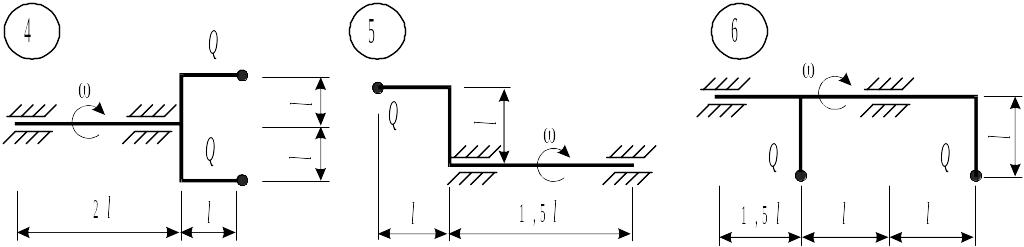
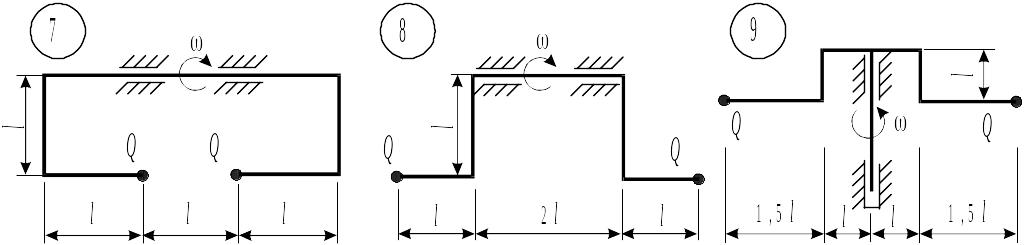
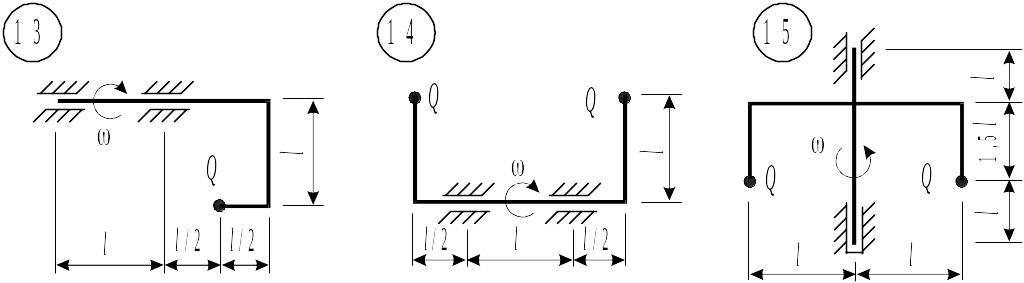
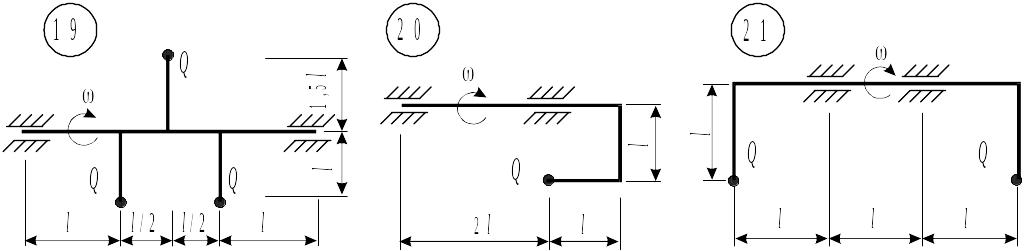
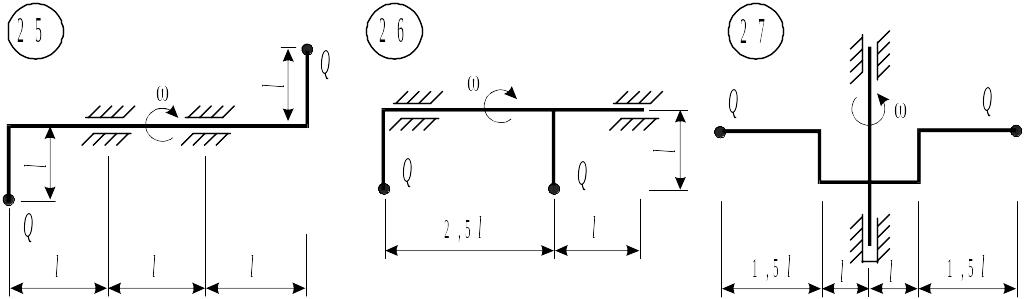
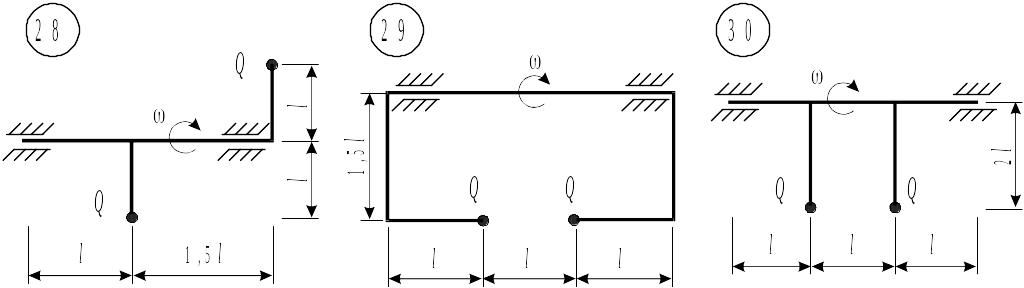
Таблица 8.1. Схемы к задаче 8

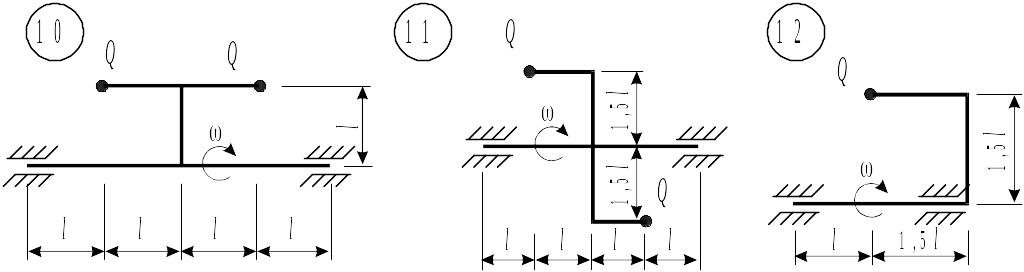
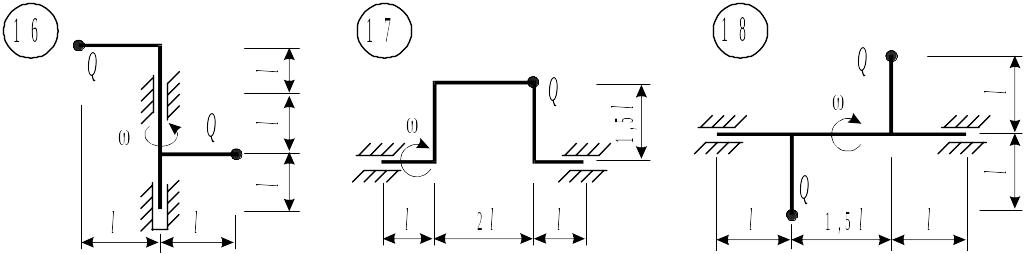
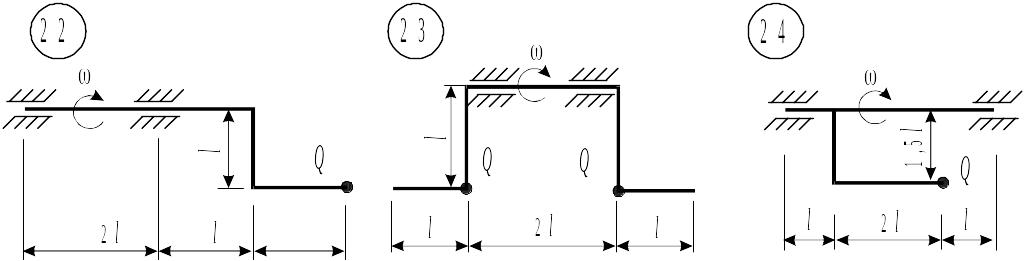
Таблица 8.1. Схемы к задаче 8 (окончание)

Таблица 8.2. Исходные значения к задаче 8

Номер варианта	Длина , мм	Вес сосредоточенного груза , Н	Диаметр стержней , мм
1	250	6	32
2	200	9	44
3	180	12	40
4	300	15	25
5	160	7	33
6	210	10	30
7	190	5	38
8	150	8	50
9	220	16	32
10	170	14	28
11	240	17	37
12	280	11	36
13	210	10	29
14	260	13	34
15	160	5	30
16	230	9	42
17	180	12	24
18	270	14	32
19	300	6	44
20	170	12	22
21	250	15	26
22	210	8	35
23	280	10	32
24	260	7	26
25	290	5	20
26	210	14	40
27	190	6	36
28	270	12	32
29	240	9	26
30	150	10	50