3. Подбор сечений
Подберём размеры указанных трёх вариантов сечений: двутавровое, кольцевое и коробчатое.
Подбор выполняем, используя условие прочности по допускаемым напряжениям (5.2). Из этого условия при значении момента Mmax = 28,8 кН·м и допускаемом напряжении 200 Мпа найдём требуемое значение момента сопротивления сечения Wx:
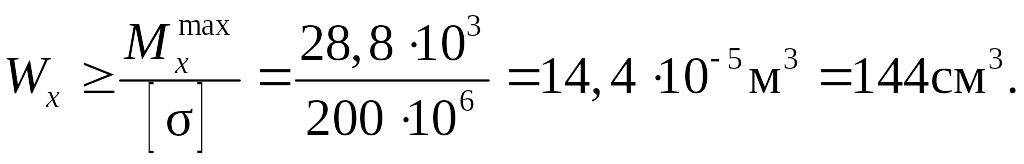
Выполним
подбор
двутаврого
сечения балки,
для
которого
момент сопротивления поперечного
сечения
По
таблице ГОСТ 8239-89 (см. табл. П.4 Приложения)
выбираем двутавр № 18, для которого
Выполним подбор диаметра кольцевого сечения балки, для которого выражение момента сопротивления сечения имеет вид:
,
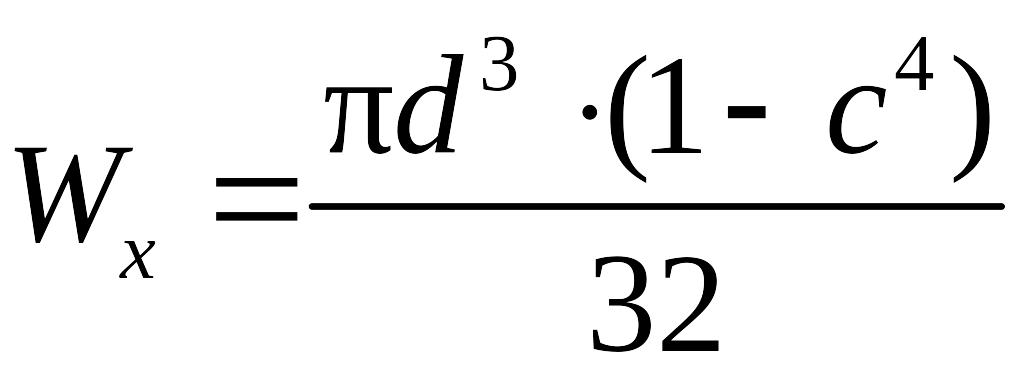где имеем согласно рисунку задаваемого сечения (рис. 5.2) отношение внутреннего диаметра к внешнему
=
0,6.
Так как момент сопротивления Wx ≥ 144 см3, то требуемый диаметр кольцевого сечения
≈
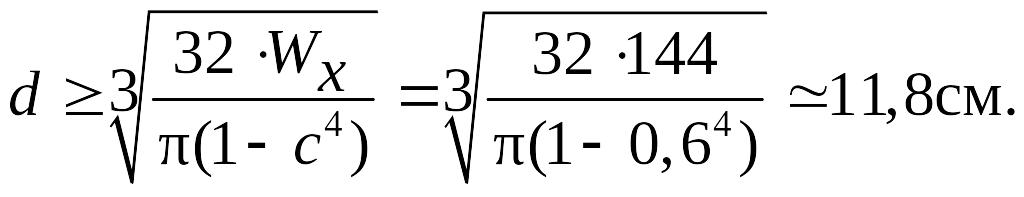Принимаем диаметр кольцевого сечения d = 12см.
Коробчатое сечение должно иметь то же значение момента сопротивления Wx ≥ 144 см3.
Запишем
выражение момента сопротивления
коробчатого сечения используя (5.3).
Сечение состоит из двух прямоугольников
размерами b
2b
и 0,6b
1,2b.
Тогда
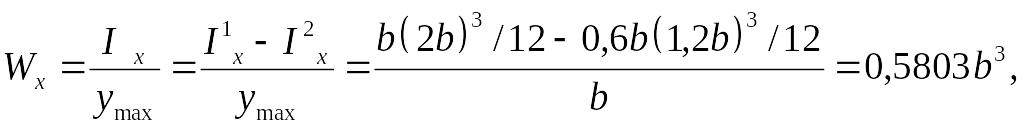
где
̶ моменты инерции прямоугольников,
вычисляемые по формуле
.
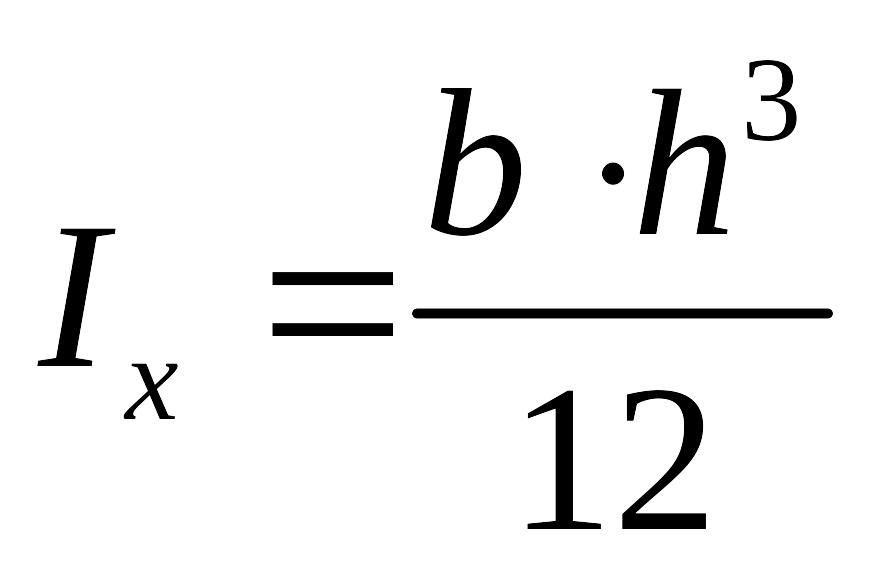Из полученного выражения момента сопротивления Wx найдём требуемое значение b:
=
.
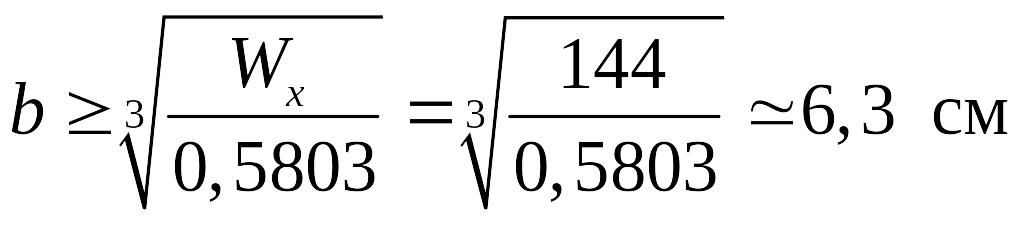Принимаем b = 6,5 см.
Сравним расход материала по площади поперечного сечения.
Для
двутавра № 18 площадь сечения по таблице
ГОСТ 8239-89 (см. табл. П.4)
Для кольцевого сечения диаметром d = 12см площадь сечения
=
Для коробчатого сечения с b = 6,5 см площадь сечения
=
Двутавровое сечение, как сечение с меньшей площадью, принимаем за более экономичное.
Таблица 5.1. Исходные значения к задаче 5
Номер варианта |
Длина участков, м |
Интенсивность нагрузки, кН/м |
Сила, кН |
Сосредоточенный момент, кН∙м |
||||
l1 |
l2 |
q1, |
q2, |
P1 |
P2 |
М1 |
М2 |
|
1 |
2,8 |
2,2 |
15 |
0 |
20 |
0 |
0 |
-32 |
2 |
2,0 |
2,6 |
0 |
-12 |
-22 |
0 |
0 |
34 |
3 |
3,0 |
1,8 |
0 |
16 |
18 |
0 |
0 |
10 |
4 |
1,9 |
2,8 |
10 |
0 |
0 |
-13 |
-20 |
0 |
5 |
2,8 |
2,0 |
14 |
0 |
12 |
0 |
18 |
0 |
6 |
2,5 |
3,0 |
-17 |
0 |
0 |
-25 |
22 |
0 |
7 |
3,0 |
2,0 |
0 |
14 |
10 |
10 |
0 |
36 |
8 |
2,2 |
2,8 |
0 |
-15 |
-26 |
0 |
0 |
-28 |
9 |
2,5 |
2,5 |
0 |
25 |
15 |
0 |
-26 |
0 |
10 |
2,0 |
2,5 |
-18 |
0 |
21 |
0 |
35 |
0 |
11 |
2,5 |
2,6 |
16 |
0 |
0 |
-20 |
-24 |
0 |
12 |
2,2 |
3,0 |
0 |
18 |
13 |
0 |
0 |
36 |
13 |
2,5 |
2,2 |
0 |
-28 |
17 |
0 |
23 |
0 |
14 |
2,3 |
2,8 |
16 |
0 |
-14 |
0 |
0 |
27 |
15 |
1,8 |
3,0 |
-26 |
0 |
21 |
0 |
-33 |
0 |
16 |
3,0 |
1,5 |
0 |
16 |
-27 |
0 |
0 |
-40 |
17 |
1,5 |
2,5 |
-30 |
0 |
-12 |
0 |
0 |
28 |
18 |
2,5 |
1,2 |
-12 |
-24 |
0 |
0 |
30 |
0 |
19 |
1,2 |
3,0 |
27 |
-12 |
0 |
0 |
0 |
-32 |
20 |
3,0 |
1,7 |
-10 |
0 |
34 |
0 |
16 |
0 |
21 |
1,6 |
2,4 |
20 |
22 |
0 |
0 |
0 |
-25 |
22 |
2,4 |
1,9 |
0 |
-20 |
-10 |
0 |
23 |
0 |
23 |
1,8 |
2,6 |
-15 |
-25 |
0 |
0 |
28 |
0 |
24 |
2,6 |
1,9 |
-30 |
19 |
0 |
0 |
0 |
-32 |
25 |
1,8 |
2,8 |
28 |
-10 |
0 |
0 |
-42 |
0 |
26 |
2,7 |
2,5 |
22 |
44 |
-15 |
0 |
0 |
27 |
27 |
2,2 |
2,8 |
-45 |
18 |
0 |
-20 |
0 |
-13 |
28 |
2,8 |
2,5 |
30 |
-15 |
0 |
0 |
0 |
-36 |
29 |
3,0 |
1,5 |
0 |
14 |
-18 |
0 |
26 |
0 |
30 |
2,3 |
1,8 |
-19 |
0 |
0 |
11 |
-16 |
0 |