2. Функцияиың жоғарғы және төменгі шектері. Енді тізбек жағдайындағыдай, функция үшін дербес шектер жиынының ең үлкен және ең кіші элементтері бар болатынын дәлелдейік.

Алдымен негізгі жағдай - локальді шенелген функцияларды қарастырайық.

Теорема. f функциясы X жиынында анықталып а нақты саны сол жиынның шектік нүктесі болсын.

Егер f функциясы а нүктесінде локальді шенелген болса, онда а нүктесінде f функциясының ең үлкен және ең кіші дербес шектері бар болады да сәйкес мына

және (5)

сандарына тең болады.

Дәлелдеуі. (5)-тегі өрнектерді былай түсіну керек: f функциясы a нүктесінде локальді шенелген болғандықтан, xX, 0<|x-a|< шарттарын қанағаттандыратын барлық х сандары үшін

|f(x)|C (6)

теңсіздігі орындалатын ₀ және С оң сандары табылады.

Егер әрбір 0<<₀ үшін анықтама бойынша

(7)

және

(8)

болcа, онда М() және m() сәйкестіктерінің әрқайсысы (0, ₀) интервалында анықталган функция болады, өйткені: біріншіден, әрбір сандар жиынының тек қана бір супремумы мен тек қана бір инфимумы болады; екіншіден, (6) бойынша

|M()|  C |m()|  C (9)

яғни M() мен m() — накты сандар.

М() және m() функциялары Бэрдің¹ сәйкес жоғарғы және төменгі функциялары деп аталады.  азайған сайын, (7) және (8) анықтамаларыидағы супремум мен инфимум анықталған жиын тарыла түседі, демек 8(I-тарау, §4)-пункттегі 2-тео- рема бойынша (0, ₀) интервалында М() - кемімейтін ал m() өспейін функция болады. Сондыктан, (9) және §5-тегі монотонды функцияның шегі туралы теорема бойынша +0 болғанда М() және m() функцияларының нақты шектері бар болады да

(10)

және

(11)

теңдіктері орындалады. (10)-дағы а саны f функциясының a нүктесіндегі дербес шектерінің ең үлкені екенін көрсетейік.

Алдымен а санының өзі дербес шек болатыныи дәлелдейік. Дербес шектің аныктамасындағы тізбегін былай кұрайық: (7) бойынша әрбір оң бүтін n саны үшін 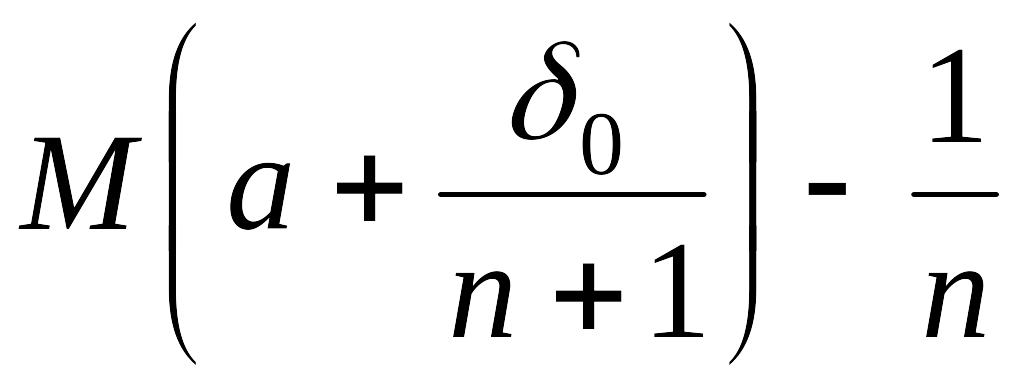саны 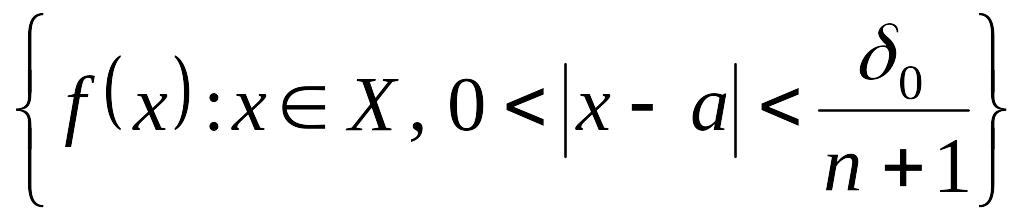жиынында жоғарғы шекарасы бола алмайды, демек,

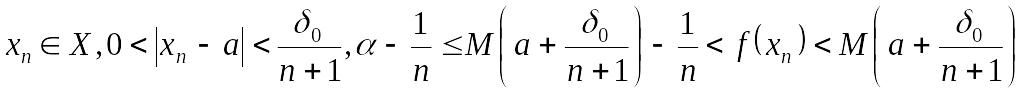(12)

теңсіздіктерін қанағаттандыратын x_n саны табылады. Бұдан nx_n тізбегі үшін (4) шарттарының орындалуы айқын. (10) мен шектің тізбектер тіліндегі анықтамасы бойынша

.

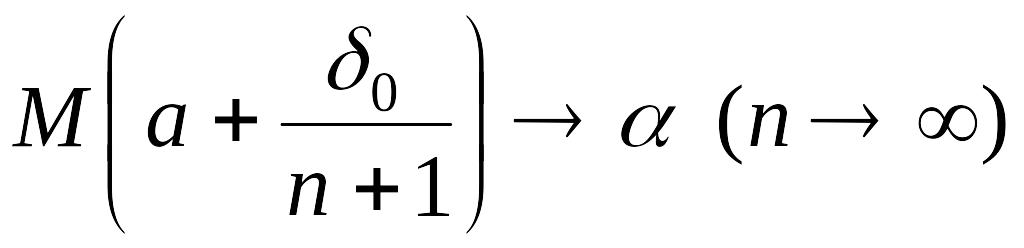демек, (12) бойынша (3 (II тарау, § 2)-пункттегі 6-теореманы қараңыз) f(x_n) (n), яғни, расында да,  саны f функциясының а нүктесіндеғі дербес шегі болады.

Енді  ең үлкен дербес шек болатынын, яғни әрбір басқа дербес шек  санынан аспайтынын көрсетейік. Сонымсн,  саны f функциясының a нүктесіндегі дербес шегі болсын. Онда дербес шектің анықтамасы бойынша (4) шарттарын канағаттандыратын белгілі бір тізбегі үшін

f (х_n)  (n). (13)

болады. _n=2x_n-a. болсын. Онда (4) бойынша _n+0 (n), демек, ((10)-ды қараңыз)

(14)

Сонымен, (13), (14) және 3 (II тарау. § 2)-пункттегі 5-теорема бойынша , өйткені _n₀ теңсіздігін қанағаттандыратын барлық оң бүтін п сандары үшіи fх_nМ_n. Теорема толық дәлелденді.

Функцияның а нүктесінде ең үлкен дербес шегін жоғарғы шек деп атап,

немесе (15)

символдарымеи белгілейді. Дәл солай, функцияның а нүктесіндегі ең кіші дербес шегін төменгі шек деп атап немесе символдарымен белгілейді.

Сөйтіп,

(16) (17)

Бұл теңдіктерде алғашқы екі өрнек қалған өрнектердің белгілеулері болады. Қолданылған белгілеулер үшін тізбектер жайында 2 (II-тарау, §5)-пунктте айтылғанды қайталауға болады.

Енді қалған жағдайларды карастырайық. Егер f функциясы a нүктесінде жоғарыдан локальді шенелмеген болса, онда сол нүктеде + оның дербес шегі болады (әрине, + ең үлкен дербес шек те болады).

Расында да, функцияның жоғарыдан локальді шенелмегендігінің анықтамасы бойынша әрбір п оң бүтін саны үшін (1(§4)-пункттегі (3) анықтамасында р=а, с=п, алу керек)

x_nХ, 0<|х_n-a|< , f(x_n)n

шарттарын қанағаттандыратын х_п саны табылады, демек, пx_n тізбегі үшін х_n a, f(x_n)+ (n) яғни + саны f функциясының a нүктесіндегі дербес шегі болады. Бұл жaғдайда да (15) белгілеулерін сақтайық. (16) теңдіктеріндегі lim немесс іпf символдарының астында тұрған өрнек + болғанда сол өрнектік бәрі де +-ке тең болсын деп келіссек, онда а нүктесінде жоғарыдан локальді шенелмеген f функциясы үшін де (16) теңдіктері орындалады.

Дәл осылай, егер f функциясы а нүктесінде төменнен локальді шенелмеген болса, онда сол нүктеде - оның дербес шегі болады (әрине, - ең кіші дербес шек те болады), тиісті келісімдерді енгізіп, (17) теңдіктерін сақтауға болады.

3. Нақты функцияның құрылысы туралы. Функцияның тербелісі. «Нақты мәнді функция» деген өте жалпы ұғым болса да, оның әрбір нүктенің қасындағы құрылысы кездейсоқ емес, белгілі бір тәртіпке бағынады екен. Оны жоғарғы және төменгі шектердің анықтамаларының салдары болатын келесі қасиеттерден көруге болады: f функциясы а нүктесінде локальді шенелген болып, а және р нақты сандары оның сол нүктедегі сәйкес жоғарғы және төменгі шектері болсын.

1⁰. Әрбір ε оң саны бойынша 0<|х-a|<() теңсіздігін қанағаттандыратын барлық хХ сандары үшін β-ε<f(x)<α+ε теңсіздіктері орындалатын () оң саны табылады.

Дәлелдеуі. Инфимумның анықтамасы бойынша әрбір >0 саны үшін М (₁())<α+ε теңсіздігін қанағаттандыратын. ₁() оң саны табылады, демек, 0<|x-а|<₁() теңсіздіктерін қанағаттандыратын барлық xX сандары үшін болады. Дәл осылай (11) мен супремумның анықтамасы бойынша әрбір >0 үшін xX, 0<|x-а|<₂()  β-ε<f(x) шарты орындалаын ₂() саны табылады. Енді бізге қажетті () саны ретінде ₁() және ₂() сандарының кішісін алсақ болғаны. Сонымен, 1⁰ дәлелденді.

2⁰. Әрбір ε және  оң саңдары үшін

xX, 0<|x-а|<, -<f(x)<+ε (18)

шарттарын қанағаттандаратын ақырсыз көп x сандары бар болады. Дәлелдеуі. (18) шарттарын қанағаттандыратын кемінде бір x саны бар болатыны дербес щеқтің «ε-» тіліндегі анықтамасынан шығады. Сондықтан, сондай х' сандары ақырсыз көп болатынын дәлелдеу қалды. Кері жорысақ, онда белгілі бір n оң бүтін саны үшін

(19)

сандарынан өзге бірде-бір х' саны (18) шарттарын қанағаттадырмайды. болсын.

(18) бойыіыца 0d болады.  жоне d оң сандары үшін дербес шектің «-d» тіліндегі анықтамасы бойынша xХ, 0а-х, -  fх  + шарттары орындалатын x саны табылады. Әрбір i = 1, 2, …, n үшін болғандықтан, .

Сонымен, (19) сандарының әрқайсысынан өзге болып, (18) шарттарын қанағаттандыратын x саны табылды (өйткені, d). яғни қайшылыққа келдік. 2° дәделденді.

Е с к е р т у. ,Бұл дәлелдеуде тек кана а накты саны f функциясының a нүктесіндегі дербес шегі болатыны пайдаланылды, демек, І-пунктте берілген дербес шектің «-d» тіліндегі анықтамасында «x саны табылады» деген сөйлемшені «...ақырсыз көп x сандары табылады» деп күшейтуге болады.

Бүл ескертуді қолданып,  нақты саны f функциясының, дербес шегі болатынын былай айтуға болады.

З⁰. Әрбір ε және  оң сандары үшін хХ, 0 х-аd, | f( х) - |   шарттарын қанағаттандыратын ақырсыз көп х сандары бар болады.

1⁰, 2⁰ және 3⁰ қасиеттерінде берілген f функциясының а нүктесінің қасындағы құрылысын бейнелейтін тәртіпті геометрия тілінде былай суреттеуге болады (29-суретті қараңыз): біріншіден, әрбір ε>0 саны үшін а-ың ойылған d-маңайындағы f фуңкциясының графигі, яғни жазықтықтың х, fх)) : хХ, 0х-а жиыншасы төбелері және болатын тік төртбұрышта жатады; екіншіден әрбір және сандары үшін төбелері және болатын тіктөртбұрыштардың әрқайсысында f функциясының графигінің ақырсыз көп нүктелері бар болады.

Сонымен a нүктасінде локальді шенелген кез келген f функциясының құрылысы екі санмен (олар өзара тең болуы мүмкін) тығыз байланыста болады. Ол сан –f функциясының a нүктесіндегі жоғарғы және төменгі шектері (Мұнда сәйкес  және  әріптерімен берілген). Біріншіден, [, ] сегментін сәл кеңейтсек (яғни, ε>0 үшін [ -ε, + ε] сегментін алсақ), онда -ның қасында (дәл айтқанда, -ның белгілі бір ойылған маңайында) қабылданған функцияның мәндерінің бәрі де сонда жатады. Екіншіден, x a-ға жақындаған сайын оған сәйкес f(x) мәндері  мен  сандарына жақындап, олардың арасында тербеліп өзгереді.

Мысалдар. 1⁰. сегментіндегі әрбір сан функциясының мәні болуы мүмкін. функциясы үшін , , сонымен бірге кез келген үшін болғанда және .