f(x)f(x_)<+

болады, демек сол жақты шектің анықтамасы бойынша

дәлірек айтқанда, теңдігі дәлелденді.

(2) және (4)-тің қалған жағдайлары дәл осылай дәлелденеді.

С а л д а р. f функциясы [a, b] сегментінде монотонды болсын. Онда a<t₁<t₂b теңсіздіктерін қанағаттандыратын t₁ және t₂ сандары үшін f кемімейтін болғанда

(6)

және f өспейтін болғанда теңсіздіктері орындалады.

Расында да, кемімейтін функция үшін (1) бойынша

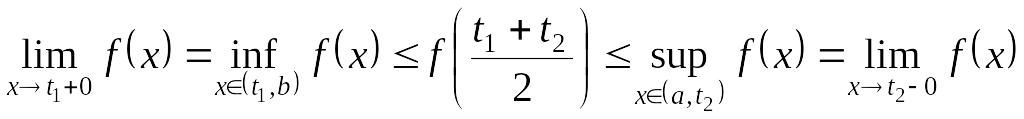
яғни (6) дәлелдеңді.

Өспейтін функция үшін де дәлелдеуі дәл осындай.

Ескерту. Дәлелденген теореманың шартында [а, b] сегментінің орнына шеткі нүктелері а(-а<+) және b(-< <b+) болатын кез келген аралықты алсақ, онда теореманың қорытындысы сақталады (тек қана (1)-мен (3)-те а=- болғанда а+0=-, ал b=+ болғанда b-0=+ деп түсіну керек). Оның дәлелдеуі ақырлы а мен b үшін келтірілген дәлелдеуден мүлдем өзгермейді, ал ақырсыз а мен b үшін тіпті қысқарады.

2. Коши критерийі. f функциясы X жиынында анықталып, а нақты саны сол жиынның шектік нүктесі болсын. Онда f функциясының а нүктесінде нақты мәнді шегі бар болуы үшін әрбір  оң саны бойынша X жиынынан алынған 0<|х-а|< және 0<|y-а|< теңсіздіктерін қанағаттандыратын кез келген х, у сандары үшін |f(х)-f(y)|< теңсіздігі орындалатындай  оң саны табылуы қажетті және жеткілікті.

Кванторлар тілінде бұл теорема былай жазылады:

f-тін анүктесінде

накты мәнді шегі  бар

(>0) (()>0) (x: хХ, 0<|х-а|<())

(y: yХ,0<|у-а|<():|f(x)-f(y)|<. (7)^:

(7)-нің оң жағында жазылған шарт Коши шарты деп аталады.

Сонымен, Коши критерийін былай айтуға болады: f(x) функциясының а нүктесінде нақты мәнді шегі бар болуы үшін сол нүктеде Коши шарты орындалуы қажетті және жеткілікті.

Әрине, кері тұжырым кұру ережесі бойынша а нүктесінде Коши шарты орындалмайтыны былай анықталады:

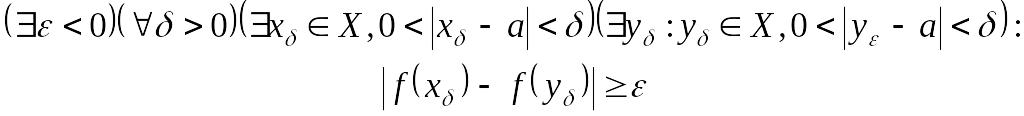(8)

яғни, сөзбен айтқанда, белгілі бір  оң саны мен кез келген  оң саны үшін функцияның f(х_)және f(у_)мәндерінің арақашықтығы -нан кіші болмайтын a-ның ойылган -маңайынан x және y нүктелері табылады. Басқаша айтқанда, f функция нүктесіңде нақты мәнді шегі жоқ болуы үшін (8)-дің орындалуы қажетті және жетклікті.

8 (§2)-Пунктте әрбір b нақты саны үшін

яғни функциясының ноль нүктесінде ешқандай нақты мәнді шегі болмайтыны дәлелденген еді.

Еңді соңғы тұжырымды қолданып, оның басқа қысқа дәлелдеуін берейік. деп алып, әрбір  оң саны үшін n_ оң бүтін санын теңсіздігін қанағаттандырарлықтай таңдап алайық. Онда және 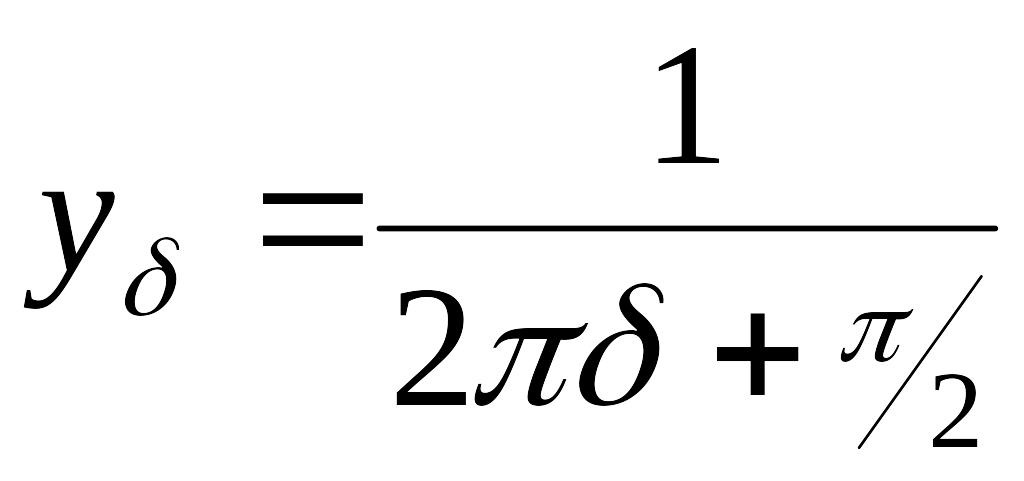үшін 0<х_<, 0<y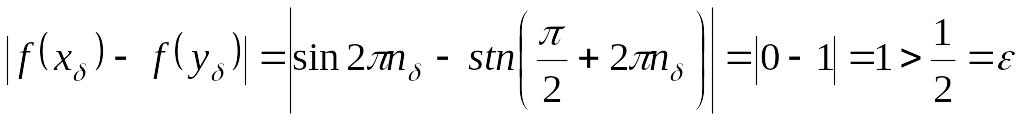_<, болады, яғни ноль нүктесінде функциясы үшін Коши шарты орындалмайды, сондықтан, оның нақты мәнді шегі де болмайды.

Коши критерийі шектің жалпы жағдайы үшін де орындалады: f функциясы X жиынында анықталсын және р(р=aR, a+0, a-0, +, -, ) сол жиынның шектік нүктесі болсын. Онда f функциясынын р-да нақты мәнді шегі бар болуы үшін әрбір  оң саны бойынша р-ның ойылган -маңайынан алынған барлық хХ және уХ сандары үшін |f(х)-f(у)|< теңсіздігі орындалатын () саны табылуы қажетті және жеткілікті.

Кванторлар тілінде бұл және оған кері теоремалар сәйкес былай жазылады:

f-тің p-да нақты

мәнді шегі бар 

және

f-тің p-да нақты

мәнді шегі жоқ 

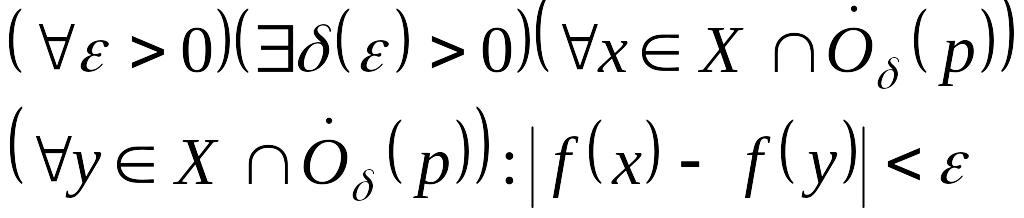
Алғашкы теореманың оң жағындағы шарт Коши шарты деп алады.

Сонымен Коши теоремасын басқаша былай айтуға болады:

f функциясының х р-ға ұмтылғанда нақты мәнді шегі бар болуы үшін р-да Коши шарты орындалуы қажетті және жеткілікті.

Екінші теорема функцияның нақты мәнді шегі .болмауы үшін ол қандай болуы керек екенін көрсетеді.

3. Коши крнтерийінің дәлелдеуі. Коши критерийінің дәлелдеуін біз тек қана р=а нақты сан болғандағы жағдайы үшін береміз. Ал жалпы жагдайда төмендегі дәлелдеуде 0<|х—а|< теңсіздігінің орнына кірістіруін қойса болғаны.

Кажеттілігі. нақты сан болсын. ε оң саны берілсін. Онда барлық 0<|x-а|< теңсіздігін қанағаттандыратын хХ үшін теңсіздігі орындалатындай δ оң саны табылады. Әрине, мынадай yX 0<|y-а|< y сандары үшін де болады, демек, аталған х пен у сандары үшін

теңсіздігі орындалады. Осыны дәлелдеу де керек еді.

Жеткіліктілігі. а нүктесінде f функциясы үшін Коши шарты орындалсын. а нүктесінде f функциясының нақты мәнді шегі бар болатынын шектің тізбектер тіліндсгі анықтамасын пайдаланып дәлелдейміз, яғни

x_nX, x_na x_n a (n  ) (9)

шарттарын қанағаттандыратын кез келген {х_n} тізбегі үшін оған сәйкес {f (х_n)} тізбегінің нақты мәнді шегі бар болатынын көрсетуіміз керек. Сонымен, (9) шарттарын канараттаңдыратын тізбегі берілсін. тізбегінің нақты мәңді шегі бар болатынын көрсетейік.

Расында да, ε оң саны берілсін. Онда (7)-нің оң жағында жазылған Коши шартындағы (ε) оң саны бойынша барлық пК үшін

0<|x-а|< (ε) (10)

теңсіздігі орындалатын К саны табылады, өйткені х_n а (п) және х_na. (7) мен (10) бойынша хК, және mК үшін |f(x_n)-f(x_m)|<ε болады, яғни {f(x_n)} тізбегі үшін Коши шарты орындалады. Сондықтан, 4(II-тарау, §З)-пунктте тізбектер үшін дәлелденген Коши критернйі бойынша тізбегінің нақты мәнді шегі бар болады, демек, 1 (§ 3)-пункттегі шектің тізбектер тіліндегі анықтамасы (шартгары азайтылған түрі) бойынша f функциясының а нүктесінде нақты мәнді шегі бар болады. Теорема толық дәлелденді.