Сигнал на выходе пиэ

(1.13)

Каждая ордината дискретной функции представляет собой -функцию, площадь которой определяется функцией В этом формальное различие между и

Изображение сигнала в смысле дискретного преобразования Лапласа определяют по формуле

(1.14)

где – дискретная функция-оригинал, – изображение.

Между выражениями (1.12) и (1.14) существует аналогия

Выражение (1.12)	Выражение (1.14)
интегрирование с пределом	бесконечная сумма
непрерывный аргумент t	дискретный аргумент nT
непрерывная функция	дискретная функция

По существу (1.14) является суммой изображений всех -функций в (1.13).

Если в (1.14) обозначить то получим Z-преобразование

(1.15)

Здесь – оригинал, – изображение в смысле Z-преобразования.

Пример.

Определить изображение единичной ступенчатой функции

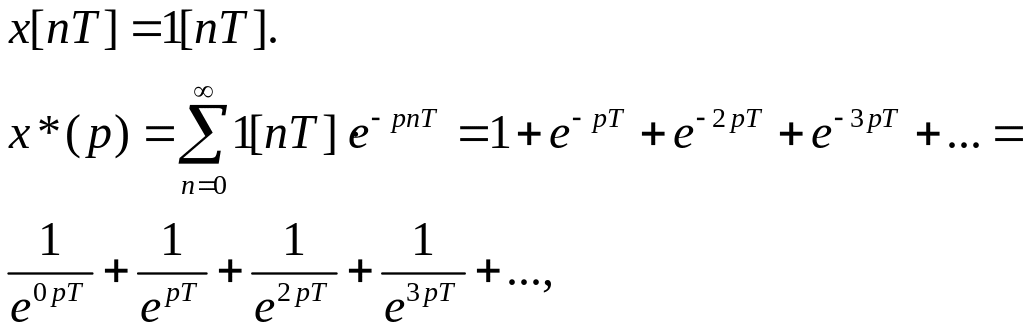
Решение.

Согласно заданию, имеем геометрическую прогрессию со знаменателем .

Сумма n-членов этой прогрессии .

.

Исходя из этого, и поэтому .

Таким образом, изображения дискретных функций являются функциями .

Аргумент Z является периодической функцией частоты. Поэтому дискретные изображения и частотные спектры дискретных функций также являются периодическими функциями частоты с периодом 2π.

1.2.4. w – преобразование: определение и свойства

Для анализа и синтеза непрерывных АСУ широко применяется частотный метод, основанный на построении логарифмических частотных характеристик. Простота и наглядность логарифмического частотного метода исследования непрерывных АСУ вызывает естественное стремление использовать метод ЛЧХ для анализа и синтеза дискретных систем [6]. Последнее возможно на основе w-преобразования.

Комплексная переменная w связана с комплексной переменной соотношением

(1.16)

Соотношение, заданное в форме (1.16), получило название w-преобразование [2-4]. Рассмотрим это преобразование подробнее, для чего запишем его в форме

(1.17)

изменяя переменную р вдоль мнимой оси плоскости Р, т.е. полагая , найдем

Правая часть этого равенства – величина мнимая, поэтому и левая часть будет мнимой величиной. Вводя обозначение , получим

или (1.18)

Переменную называют псевдочастотой, так как это безразмерная величина. Реальная частота связана с псевдочастотой соотношением

(1.19)

Для исследования импульсных и цифровых систем в ряде случаев более удобна размерная псевдочастота , которая связана с псевдочастотой зависимостью

(1.20)

Тогда

(1.21)

Переменную  называют абсолютной псевдочастотой. Из выражения (1.20) следует, что при <<2 абсолютную псевдочастоту  в расчетах и при построении ЛЧХ можно заменять действительной частотой .

Соотношение (1.16) может быть представлено с учетом (1.21)

(1.22)

Поясним смысл преобразования (1.16). Использование подстановки при замене р на позволяет отобразить левую полуплоскость плоскости Р внутрь круга единичного радиуса плоскости Z. Функция является периодической функцией с периодом , поэтому для обхода всей окружности единичного радиуса достаточно изменять частоту в интервале или в интервале . При этом отрезок мнимой оси от до преобразуется в окружность единичного радиуса (рис. 1.20, а, б).

С помощью соотношения (1.16) возможно отображение всех точек Z-плоскости, расположенных внутри круга единичного радиуса, в соответствующие точки левой полуплоскости w. Подобные отображения получили название конформных отображений (рис. 1.20, б, в).

При изменении частоты в интервале абсолютная псевдочастота принимает все значения, принадлежащие интервалу .

На рис. 1.21 представлен график значений псевдочастоты.

Операция w-преобразования в виде

конформно отображает левую полуполосу , Re q<0 плоскости q (иначе р) на левую полуплоскость плоскости w, причем мнимая положительная полуось плоскости w является образом отрезка мнимой положительной полуоси плоскости q длиной . Начало этого отрезка находится в начале координат.

Понятие псевдочастоты позволяет строить так называемые логарифмические псевдочастотные характеристики дискретных АCУ.

p

z

w

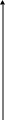
Im Im

Im

=+- /T 1  0

0

Re =0 Re Re

-

а) б) в)

Рис. 1.20. Иллюстрация w-преобразования

-3 -2 - 0 2 3

-

Рис. 1.21. График значений псевдочастоты