1.2. Математическое описание дискретных систем

1.2.1. Решетчатые функции

Математическое описание импульсных АСУ усложняется из-за дискретного характера сигнала. Квантованный по времени сигнал может быть представлен выборкой ординат непрерывной функции времени (см. рис.1.1). Эти ординаты разделены периодом квантования, а внутри периодов все промежуточные значения равны нулю. Поэтому дискретный сигнал удобно описывать функциями дискретной переменной [6].

Рассмотрим функцию времени , определенную для всех значений t и тождественно равную нулю для (см. рис. 1.1).

Пусть n – натуральное число (n=0,12,3…) и Т – период дискретности. Функцией дискретного аргумента называется числовая последовательность f[0], f[T], f[2T],…, f[nT], получающаяся в результате выборки значений функции в точках , n – натуральное число. Для краткости ее называют решетчатой функцией и обозначают f[n].

При заданном интервале дискретности Т по функции решетчатая функция f[n] определяется однозначно. Непрерывная функция – огибающая для своей решетчатой функции f[n]. Но поскольку через дискретные точки решетчатой функции можно провести множество огибающих, то обратного соответсвия между решетчатой функцией и “породившей” ее функцией нет: f[n] .

Если необходимо определять значения функции между точками квантования, то вводят понятие смещенной решетчатой функции.

Смещенной решетчатой функцией называется числовая последовательность – f[T], f[T+T],…, f[iT+T],…, f[nT+T], 0    1, образованная в результате выборки значений функций в точках оси времени, где  – постоянное число, лежащее в интервале 0   1. Сокращенно f[n, ].

Поскольку значения решетчатой функции известны только для дискретных значений аргумента, то для изучения поведения таких функций методы дифференциального и интегрального исчисления оказываются непригодными.

Для оценки свойств решетчатой функции используется аппарат конечных разностей и конечных сумм, позволяющий оценивать свойства числовых последовательностей (функций дискретного аргумента).

Для исследования динамики дискретных импульсных АСУ используются разностные уравнения. Их решение, так же как и дифференциальных, представляет известные трудности. В связи с этим, в теории дискретных (импульсных) АСУ широко используются операционные методы.

1.2.2. Разностные уравнения

Если вместо переменной t ввести относительную переменную , то непрерывной функции в относительном масштабе будет соответствовать решетчатая функция . Она совпадает с при

(1.1)

Таким образом, решетчатая функция изменяет свое значение при целочисленных значениях независимого переменного n, а интервал между дискретами равен 1.

Дискретная функция не является однозначной, что видно из рис. 1.15.

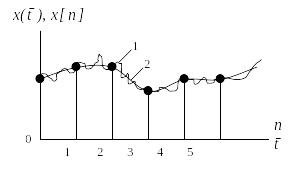
Рис. 1.15. Решетчатая функция

Для устранения этой неоднозначности вводят смещенные дискретные функции, позволяющие “просматривать” процессы внутри периодов Т.

Записывают смещенную функцию так

. (1.2)

Однако на основе теоремы Котельникова можно сделать вывод, что если непрерывный сигнал не содержит гармоническую составляющую с частотой выше , то при квантовании с периодом дискретная решетчатая функция точно отобразит непрерывную функцию, т.е. потери информации при дискретизации не будет.

Для математического описания динамики дискретных систем применяют разностные уравнения. Они определяют связь между значениями решетчатой функции и, таким образом, форму огибающей данной решетчатой функции. Оценка связи значений решетчатой функции производится с помощью конечных разностей. Они являются аналогами производных в дифференциальных уравнениях.

Переход от дифференциальных уравнений к разностным основан на замене производных разностями соответствующих порядков (табл. 1.1).

Таблица 1.1

Соответствие производных и правых разностей

Порядок производной или разности	Непрерывная функция	Дискретная функция
1
2
.	. . .	. . .
m

Первая разность решетчатой функции:

,

и т.д.

То есть, для определения первой разности (рис. 1.16) надо знать два последовательных значения решетчатой функции.

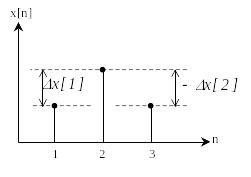
Рис. 1.16. К определению разностей решетчатой функции

Упомянутая выше аналогия между первой разностью и первой производной видна из того, что первая разность, как и первая производная, равна по существу, отношению приращения функции к приращению аргумента

,

но так как

,

то ее значение просто равно .

Вторая разность решетчатой функции:

Для нахождения второй разности надо знать три последовательных значения решетчатой функции. Разность m-го порядка определяется выражением

Рассмотрим простой пример дискретной функции и ее первой разности (рис. 1.17). Пусть . Ее первая разность т.е. является единичной ступенчатой дискретной функцией . Вторая и высшие разности этой функции равны нулю.

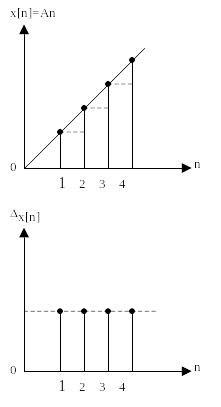
Рис. 1.17. Пример дискретной функции и ее первой разности

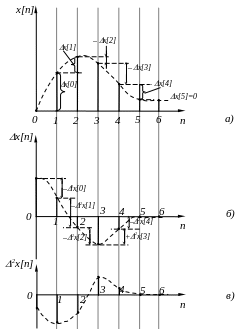
На рис. 1.18 в качестве примера приведена решетчатая функция произвольного вида x[n] (рис. 1.18, а), а также ее первая x[n] (рис. 1.18, б) и вторая ²x[n] (рис. 1.18, в) разности.

Разностное уравнение k-го порядка соответствует дифференциальному уравнению k-го порядка. Если линейное дифференциальное уравнение записывают в виде

(1.3)

то линейное разностное уравнение с постоянными коэффициентами можно записать так

(1.4)

где – известная дискретная функция;

– искомая дискретная функция, получаемая в результате решения разностного уравнения.

Рис. 1.18. Решетчатая функция произвольного вида x[n],

а также ее первая x[n] и вторая ²x[n] разности

Дифференциальное уравнение можно рассматривать как предельное выражение для разностного уравнения при . Решать разностные уравнения можно различными методами, аналогичными методам решения дифференциальных уравнений.

В теории управления часто применяют операционный метод решения дифференциальных уравнений, который позволяет свести решение к решению алгебраического уравнения.

Для решения разностных уравнений также используют операционный метод, основанный на дискретном преобразовании Лапласа, в частности Z-преобразовании.