- •Днепропетровск нМетАу 2014
- •Содержание
- •Часть 1. Теория дискретных систем автоматического
- •Часть 2. Лабораторный практикум 58
- •Введение
- •Часть 1. Теория дискретных систем автоматического управления
- •1.1. Общая характеристика дискретных систем
- •1.1.1. Понятие и классификация дискретных асу
- •1.1.2. Виды импульсной модуляции. Теорема Котельникова-Шеннона
- •X(t) – сигнал рассогласования, входной сигнал иэ;
- •X*(t) – импульсный сигнал с выхода иэ; y(t) – выходной сигнал
- •1.1.3. Примеры дискретных систем
- •1.2. Математическое описание дискретных систем
- •1.2.1. Решетчатые функции
- •1.2.2. Разностные уравнения
- •1.2.3. Понятие о z-преобразовании
- •Сигнал на выходе пиэ
- •Между выражениями (1.12) и (1.14) существует аналогия
- •1.2.5. Математическая модель импульсного элемента
- •1.2.6. Частотные характеристики импульсного звена
- •1.2.7. Модель формирующего элемента и импульсной асу
- •1.2.8. Передаточные функции импульсных асу
- •1.3. Устойчивость и качество дискретных систем
- •1.3.1. Условия устойчивости
- •1.3.2. Критерии Найквиста и Михайлова
- •1.3.3. Показатели качества импульсных систем
- •1.4. Синтез дискретных систем
- •1.4.1. Замена дискретной системы эквивалентной непрерывной системой
- •1.4.2. Цифровые пид-регуляторы
- •1.4.3. Особенности реализации дискретной коррекции
- •1.5. Основные понятия о цифровых асу
- •Часть 2. Лабораторный практикум
- •1.1. Общие сведения о дискретной асу, квантовании и модуляции
- •1.2. Структурные схемы дискретных асу
- •2. Порядок выполнения работы
- •2.1. Моделирование процесса квантования по уровню
- •2.2. Моделирование процесса квантования по времени
- •2.3. Моделирование кодо-импульсной модуляции
- •Контрольные вопросы
- •Лабораторная работа №2 Решение разностных уравнений
- •1. Краткие теоретические сведения
- •1.1. Решение разностных уравнений с помощью характеристического полинома
- •1.2. Решение разностных уравнений с помощью z-преобразования
- •2. Методические указания
- •2.1. Задание и таблица вариантов
- •2.2. Задание и таблица вариантов
- •Контрольные вопросы
- •Лабораторная работа №3 Расчет и исследование импульсной асу
- •1. Краткие теоретические сведения
- •1.1. Методика построения математической модели линейной иасу
- •1.2. Последовательность расчета и моделирования иасу на примере
- •2. Методические указания
- •2.1. Задание и таблица вариантов
- •2.2. Порядок выполнения работы
- •Контрольные вопросы
- •1. Краткие теоретические сведения
- •Аср температуры в эп
- •1.2. Параметрическая идентификация ор по переходной характеристике (кривой разгона)
- •1.3. Синтез аср температуры в рабочем пространстве эп
- •1.3.1. Синтез аср температуры с непрерывным регулятором
- •1.3.2. Синтез аср температуры с шим-регулятором
- •2. Методические указания
- •2.1. Задание и таблица вариантов
- •2.2. Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Теория автоматического управления импульсные асу
- •49600, Днепропетровск, пр. Гагарина, 4
1.1.2. Виды импульсной модуляции. Теорема Котельникова-Шеннона
Характерной особенностью импульсных систем автоматического управления является то, что хотя бы одна из переменных является квантованной по времени. Эти квантованные по времени величины при помощи импульсной модуляции преобразуются в последовательность импульсов, которые в дальнейшем воздействуют на непрерывную часть системы. Таким образом, техническую процедуру получения последовательности импульсов, несущих информацию о дискретных значениях сигнала, называют импульсной модуляцией.
Процесс квантования и импульсной модуляции осуществляется импульсным элементом. Импульсную систему в общем случае можно представить в виде импульсного элемента (ИЭ) и непрерывной части (НЧ) (рис. 1.3) [2-4].

Рис.1.3. Типовая структурная схема ИАСУ: u(t) – входной сигнал;
X(t) – сигнал рассогласования, входной сигнал иэ;
X*(t) – импульсный сигнал с выхода иэ; y(t) – выходной сигнал
Импульсный элемент преобразует непрерывно изменяющуюся величину x(t) в последовательность модулированных импульсов x*(t), осуществляя при этом квантование сигнала (рис. 1.4, а) и модуляцию (рис. 1.4, б).
а)
б)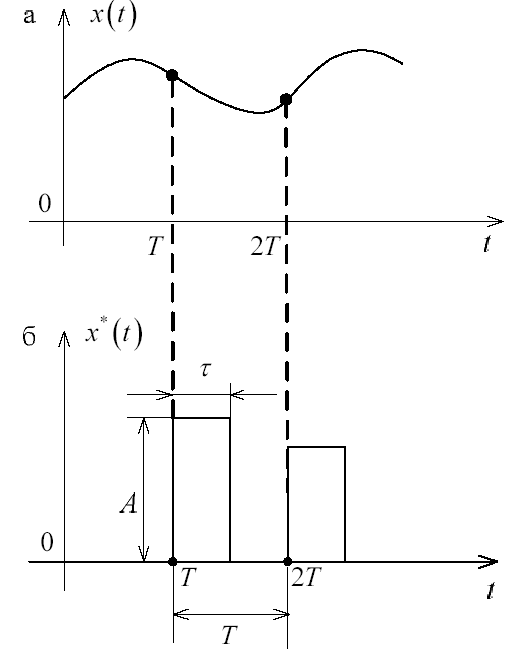
Рис.1.4. Временные диаграммы работы ИЭ:
а – непрерывный сигнал x(t); б – сигнал на выходе импульсного элемента x*(t)
Процесс импульсной модуляции состоит в изменении по определенному закону какого-либо параметра периодически повторяющихся импульсов.
Величина, определяющая закон модуляции, называется модулирующей величиной.
Основными параметрами импульсной последовательности являются:
А – амплитуда (высота) импульса; – длительность (ширина) импульса;
Т – период квантования (повторения, дискретности);
![]() – частота
повторения.
– частота
повторения.
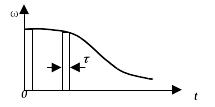
В зависимости от того, какой параметр последовательности импульсов изменяется, различают следующие виды модуляции (рис. 1.5):
амплитудно-импульсную модуляцию (АИМ), при которой амплитуда импульса пропорциональна входному сигналу (рис. 1.5, в);
широтно-импульсную модуляцию (ШИМ), при которой длительность импульса пропорциональна входному сигналу (рис. 1.5, г);
время-импульсную модуляцию (ВИМ), включающую в себя фазо-импульсную модуляцию (ФИМ), когда фаза или временной сдвиг импульса относительно начала периода дискретности Т пропорциональна входному сигналу (рис. 1.5, д), и частотно-импульсную модуляцию (ЧИМ) – частота дискретности пропорциональна входному сигналу.
Наибольшее распространение получили импульсные системы с АИМ.
x




 x(t)
x(t)
0 а)
x(t) – непрерывный сигнал,
а)
x(t) – непрерывный сигнал,
Т t T – период квантования
x



x[nT]

 б)
x[nT] – решетчатая функция
б)
x[nT] – решетчатая функция
T nT t
y





![]() x в) АИМ:
x в) АИМ:

 длительность
длительность
![]()
 (0<<1),
(0<<1),
t величина импульса x[nT]
y ![]()




![]() г)
ШИМ:
г)
ШИМ:
![]()
![]()

![]()




![]() t
t
![]()
y
![]()
д) ФИМ:

![]()
T nT t
![]()
Рис. 1.5. Виды модуляции
К основным достоинствам импульсных систем, как было отмечено ранее, относят возможность многоточечного управления, многократное использование линий связи, повышенную помехозащищенность.
Важным классом ИАСУ являются линейные импульсные системы, в которых связь между выходом и входом описывается линейным оператором, например, линейными разностными уравнениями. Из всех разновидностей ИАСУ только ИАСУ с АИМ являются линейными при условии линейности непрерывной части.
Далее будем рассматривать только этот класс систем.
Импульсную систему (ИС) можно представить в виде соединения импульсного элемента (ИЭ) и непрерывной части, причем система может быть как замкнутой (рис. 1.6, а), так и разомкнутой (рис. 1.6, б).
|
|
а) |
б) |
Рис. 1.6. Импульсная система
Действие импульсного элемента можно представить так, как это показано на рис. 1.7.
Он
представляет собой периодически
замыкаемый ключ, на выходе которого
через равные промежутки
![]() вырабатываются импульсы, амплитуда
которых соответствует непрерывному
сигналу.
вырабатываются импульсы, амплитуда
которых соответствует непрерывному
сигналу.
|
|
|
Рис. 1.7. Действие импульсного элемента
Реальные ИЭ характеризуются конечной длительностью импульса, а процессы замыкания и размыкания существенно влияют на его форму. Это затрудняет исследование ИС. Поэтому при математическом описании реальные импульсные элементы заменяют идеализированными моделями.
Одна из таких представлена на рис. 1.8.
Она представляет последовательное соединение идеального или простейшего импульсного элемента ПИЭ и формирующего элемента ФЭ.
В
простейшем импульсном элементе замыкание
и размыкание происходят мгновенно, а
на выходе вырабатываются импульсы типа
![]() функций
с нулевой длительностью на конечной
“площадке”.
функций
с нулевой длительностью на конечной
“площадке”.
ПИЭ |
Рис. 1.8. Идеализированная модель реального ИЭ
Надо иметь ввиду, что амплитуда мгновенных импульсов на выходе ПИЭ бесконечно велика, а высота импульсов на рис. 1.8 лишь условно соответствует их площади.
Обычно последовательность импульсов в автоматической системе управления (АСУ) используется для выработки управляющих воздействий и является промежуточным носителем информации. Результат же работы АСУ должен быть эквивалентен результату работы непрерывной системы. Поэтому последовательность импульсов должна нести всю необходимую информацию, содержащуюся в непрерывном сигнале. Однако часть информации теряется при квантовании. Чем реже квантуется непрерывный сигнал, тем больше теряется информации, и тем труднее восстановить форму сигнала после преобразования его в импульсном элементе.
Поэтому
выбор частоты преобразования необходимо
увязывать с формой входного сигнала.
Условия для выбора частоты определяются
на основе теоремы
Котельникова-Шеннона:
непрерывный сигнал
![]() с ограниченным частотным спектром в
пределах от
с ограниченным частотным спектром в
пределах от
![]() до
до
![]() полностью определяется последовательностью
своих дискретных значений, следующих
через интервал прерывания
полностью определяется последовательностью
своих дискретных значений, следующих
через интервал прерывания
 (или частоту прерывания
(или частоту прерывания
![]() ).
Эта теорема определяет условие, при
котором непрерывный сигнал может быть
восстановлен после квантования без
искажения: это возможно, если частота
квантования в два раза и более превышает
предельную частоту в спектре непрерывного
сигнала.
).
Эта теорема определяет условие, при
котором непрерывный сигнал может быть
восстановлен после квантования без
искажения: это возможно, если частота
квантования в два раза и более превышает
предельную частоту в спектре непрерывного
сигнала.
Сигналы в АСУ всегда имеют ограниченный спектр ввиду ограниченности полос пропускания отдельных реальных элементов. Поэтому практически всегда условие по ограниченности спектра непрерывного сигнала выполняется.


 Error: Reference source not found
Error: Reference source not found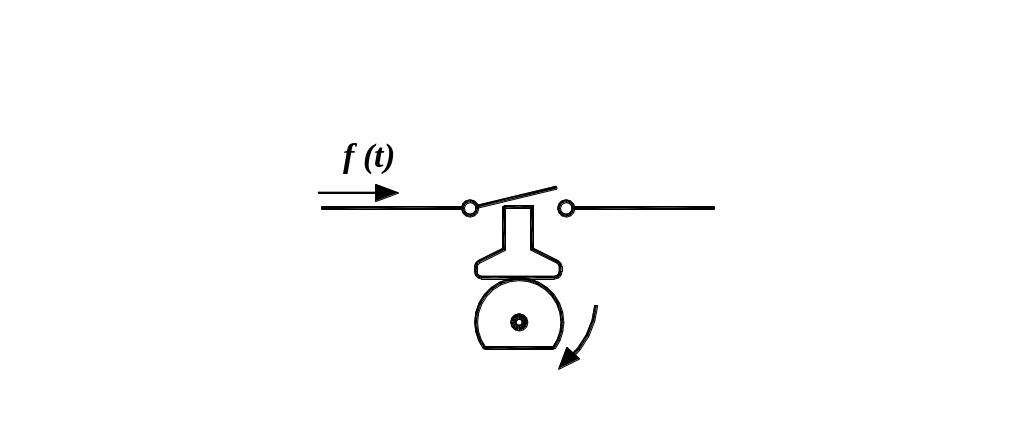
 Error: Reference source not found
Error: Reference source not found