Контрольные вопросы

Даны разностные уравнения:

1) ,	2) ,
3) ,	4) ,
5) ,	6) ,
7) ,	8) ,
9) ,	10)
11) ,	12) ,
13)	14)

Требуется решить уравнение:

а) с помощью характеристического уравнения;

б) при помощи z-преобразования.

Лабораторная работа №3 Расчет и исследование импульсной асу

Цель работы – исследование математических моделей линейных импульсных систем и способов построения этих моделей для непрерывных объектов; изучение влияния параметров непрерывной части системы и периода квантования на характеристики импульсной системы

1. Краткие теоретические сведения

1.1. Методика построения математической модели линейной иасу

Импульсная система отличается от непрерывной наличием импульсного элемента (ИЭ), осуществляющего квантование сигнала по времени. Импульсный элемент преобразует непрерывный входной сигнал в последовательность модулированных импульсов.

С

W₀(p)

труктурная схема исследуемой в данной работе системы приведена на рис. 3.1, где u(t) – входное задающее воздействие, x(t) – сигнал рассогласования (входной сигнал ИЭ), x^*(t) – импульсный сигнал с выхода ИЭ (дискретное управление), y(t) – выходной сигнал.

Рис. 3.1. Структурная схема одноканальной замкнутой

дискретной системы управления

Дискретное управление на выходе импульсного элемента (ИЭ) изменяется в строго определенные моменты времени, связанные с шагом квантования T, а все остальное время остается постоянным. Такой ИЭ называют фиксатором нулевого порядка. Дискретную модель линейного объекта управления (НЧ) с фиксатором нулевого порядка на входе можно получить, используя решение линейного дифференциального уравнения, описывающего объект

(3.1)

, ,

, , .

Разностное уравнение для этого объекта имеет вид

(3.2)

где ,

( при условии ).

Для расчета матриц A и B используют разложение матричной экспоненты в ряд

, . (3.3)

Матрицы и C совпадают.

Дискретную математическую модель линейного непрерывного объекта с передаточной функцией W₀(p) и фиксатором нулевого порядка (см. рис. 3.1) на входе можно получить, используя Z-преобразование

. (3.4)

В табл. 1.2 (стр.22) приведены выражения Z-преобразований для некоторых функций времени. Сложную передаточную функцию перед преобразованием следует разложить на элементарные дроби.

1.2. Последовательность расчета и моделирования иасу на примере

Функциональная схема импульсной АСУ приведена на рис. 3.2.

W₁(p) и W₂(p) – передаточные функции звеньев:

, .

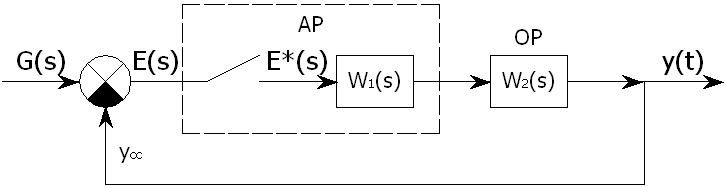
Рис. 3.2. Функциональная схема импульсной АСУ:

ОР – объект регулирования, АР – автоматический регулятор

Преобразованная функциональная схема импульсной АСУ с фиксатором нулевого порядка приведена на рис. 3.3.

Рис. 3.3 Преобразованная функциональная схема импульсной АСУ

Передаточная функция фиксатора нулевого порядка: .

В результате свертки функциональная схема ИАСУ примет вид (рис. 3.4).

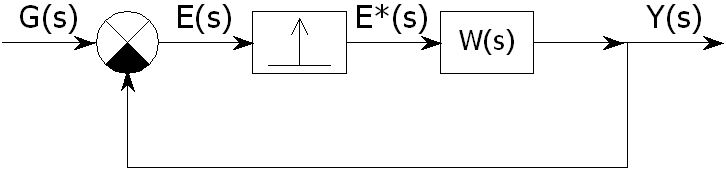
Рис. 3.4. Свернутая функциональная схема АСУ

1.2.1. Запишем передаточную функцию непрерывной части системы:

.

Схема z-модели АСУ имеет вид (рис. 3.5).

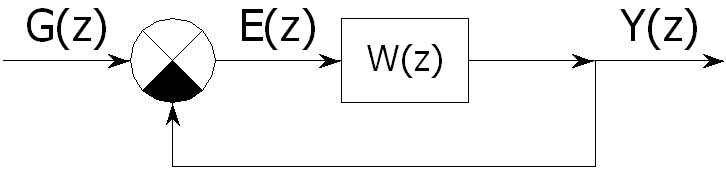
Рис. 3.6. Схема z-модели АСУ

1.2.2. Определим z-изображение передаточной функции разомкнутой АСУ:

,

т.к. , то

.

Правую часть выражения необходимо представить в виде суммы простых дробей с переменной z в числителе. Разложение можно выполнить методом неопределенных коэффициентов или в пакете Matlab с помощью команды [R,P,K]=residue(B,А).

z-изображение передаточной функции разомкнутой АСУ W(z) может быть получено с помощью следующих команд Control System Toolbox пакета Matlab:

>> W1=tf([1],[0.8 0]);

>> W2=tf([1],[0.8 1]);

>> W=series(W1,W2);

>> Wz=c2d(W,1,'zoh')

Transfer function:

0.5365 z + 0.3554

----------------------

z^2 - 1.287 z + 0.2865

Sampling time: 1 – период дискретизации.

1.2.3. Передаточную функцию замкнутой ИАСУ определим по формуле

или с помощью функции Control System Toolbox пакета Matlab:

>> Fiz=feedback(Wz,1)

Transfer function:

0.5365 z + 0.3554

---------------------

z^2 - 0.75 z + 0.6419

Sampling time: 1 – период дискретизации.

1.2.4. Найдем z-изображение выходного сигнала:

, т.к. для .

.

1.2.5. Выходной сигнал можно определить с помощью обратного z-преобразования: . Переходная характеристика замкнутой ИАСУ (рис. 3.7) может быть получена с помощью команды step Control System Toolbox пакета Matlab:

>> step(Fiz);grid

Рис. 3.7. Переходная характеристика замкнутой ИАСУ

1.2.6. Моделирование импульсной АСУ может быть также выполнено в Matlab/Simulink. Схема z-модели, рассматриваемой в данном примере, показана на рис. 3.8.

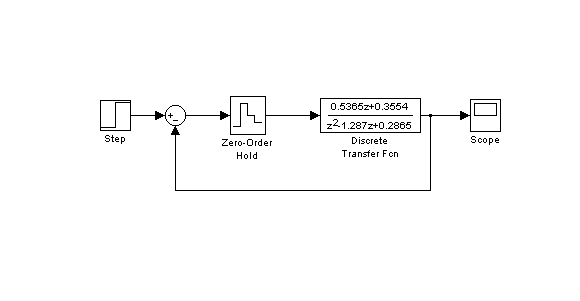
Рис. 3.8. Схема z-модели ИАСУ